考虑迟滞特性的卡尔曼滤波和门控循环单元神经网络的锂离子电池SOC联合估计 *

胡明辉，朱广曜，刘长贺，唐国峰

（1. 重庆大学，高端装备机械传动全国重点实验室， 重庆 400044；2. 重庆大学机械与运载工程学院， 重庆 400044）

前言

近年来，能源危机和环境污染已成为全球亟待解决的重大问题，广泛发展电动汽车对于缓解甚至解决这两大急迫难题具有积极的作用，已成为世界各国的重要愿景［1-2］。锂离子电池因为：（1） 循环寿命长；（2） 高能量密度、功率密度及效率；（3） 标称电压高、自放电率低等优势成为电动汽车的最佳能源选择［3-5］。为保障并延长电池的应用寿命，在充放电过程中须采取预防和监管措施，如若出现过电压、电流及功率限度可能造成电池单体损毁甚至热失控等安全问题［6-8］，因此在汽车控制系统中需要增添先进的动力电池管理系统（battery management system，BMS），其目的是监测和优化电池的各种行为及状态，并控制其安全地发挥最佳性能［9-10］。

由于电池材料的特性，开路电压与荷电状态并不是一一映射的关系曲线［11］。电池从0%SOC持续充电至100%SOC，再从100%SOC持续放电至0%SOC，会在持续充放电的OCV曲线之间形成一个开路电压区间，但由于电池电压在电流大小和方向发生骤变时受到迟滞特性的影响，在不完全充放电循环过程中，SOC和OCV的关系曲线存在迟滞回环，在相同的SOC下，不同充放电路径的电池开路电压会有所不同，通常充电开路电压（OCVcha）高于放电开路电压（OCVdis）［12］。

越来越多的学者对迟滞特性的原理展开深入研究并对其进行解释。Zhu 等［13］通过热力学试验发现，应变能导致的热力学效应会引起磷酸铁锂电池产生迟滞特性。林春景等［14］认为电池在充放电过程中，锂离子从正极材料中的脱出或嵌入造成正极材料的相变，其产生或消耗的能量使电池在充电时的开路电压升高，在放电时的开路电压降低。Lu 等［15］指出，活性物质表面的机械应力阻碍了锂化，所以需要更高的电势才能克服。因此迟滞回环的充电电压曲线保持在持续充电的OCV曲线下方，迟滞回环的放电电压曲线保持在持续放电的OCV曲线上方，且随着充/放电过程的进行逐渐趋向于持续充/放电的OCV曲线。

锂离子电池内部电化学反应复杂，且易受到内外部环境的影响［16］。为确保BMS 精确可靠地发挥功能，需要对电池荷电状态进行准确而实时的估计。目前SOC的估计方法主要分为3 种：安时积分法、基于模型滤波算法的方法以及基于数据驱动的估计方法［17］。安时积分法利用SOC定义进行估计，是目前最常用而简单的SOC估计方法，但其估计精度易受初始SOC和电流传感器测量精度的影响，且积分运算造成了随时间而逐渐累积的误差［18］。基于模型滤波的方法中卡尔曼滤波系列表现尤为突出，为解决非线性问题，扩展卡尔曼滤波算法将强非线性系统通过泰勒级数展开非线性函数，但忽略2 阶以上的高阶项导致一定的估计误差［19］。考虑到电池SOC估计是一个基于时间序列数据的预测问题，当前时刻SOC的估计值取决于历史的测量信息和当前的测量数据，而基于数据驱动方法的循环神经网络（recurrent neural network， RNN）具有存储历史信息的记忆单元，根据当前时刻的输入数据对未来结果进行预测，所以RNN 能够较好地适用于电池SOC的估计［20］。

基于模型的估计方法首先须建立电池模型，其中电特性建模的目的在于模拟各种负载条件下锂离子电池的电压响应。现有电特性模型具体分为数据驱动/黑箱模型、电化学机理模型及等效电路模型［21］。综合考虑模型的精度与复杂度，在工程应用上等效电路模型的适用性最广泛［22］。Wehbe等［23］发现由于迟滞特性的影响，等效电路模型表现出局限的准确性。Kim 等［24］采用磷酸铁锂电池充放电试验的开路电压测量数据，基于简单的等效电路模型，分别用两条单独的OCV-SOC曲线代表电池的充电和放电过程，体现了电池的迟滞特性。Kwak 等［25］在1阶RC等效电路模型中考虑迟滞特性，并利用最小二乘法对模型参数进行辨识，试验测试表明该方法与扩展卡尔曼滤波器的估计方法相比更有效。Tran等［26］将迟滞特性集成在1 阶RC 模型上，并将其应用于动态和非动态工况。结果表明，考虑迟滞特性能够提高1 阶RC 模型端电压的估计精度。然而1 阶RC 模型无法较好地区分电池的电化学极化和浓度极化，为进一步提高模型的估计精度，提出2 阶RC模型并广泛应用于工程实践，但其缺乏迟滞特性影响的深入研究，进而引起迟滞电压对电池状态估计的误差。

基于上述文献回顾及相关内容，本文中通过电池迟滞特性的分布建立了一种考虑迟滞特性的2 阶RC 等效电路模型，并采用带有遗忘因子的递推最小二乘法进行模型参数在线辨识。针对电池荷电状态估计提出了一种联合门控循环单元（gated recurrent unit， GRU）神经网络和自适应扩展卡尔曼滤波（adaptive extended Kalman filter， AEKF）的估计方法，以AEKF的估计结果为模型值，以GRU神经网络的估计结果为测量值，通过卡尔曼滤波（Kalman filter， KF）得到最终的SOC估计结果，并作为下一时刻AEKF 的输入。最后在常温、低温及变温环境下进行对比验证，从准确性和鲁棒性等方面比较迟滞特性对等效电路模型的影响以及不同算法对SOC的估计。结果表明，考虑迟滞特性能够进一步提高模型的精度，所提出的联合估计法能够改善噪声协方差的自适应性及SOC估计的准确性。

1 电池试验

1.1 研究对象的选择

我国汽车行业现今主要以磷酸铁锂电池和三元锂电池为主，两者优势互补。三元锂电池具有比能量高、低温性能好、电压平台高等优势；而磷酸铁锂电池拥有良好的耐高温性，其安全性能及循环使用寿命较高，且由于正负极材料（磷酸铁锂和碳）易获取，使其成本较低。考虑到本文试验完成的循环次数达到150 次左右，而老化效应对试验结果造成不可忽视的影响，且迟滞特性方面的研究对磷酸铁锂电池的意义更大。因此本文选择磷酸铁锂电池为研究对象，具体的基本参数如表1所示。

表1 磷酸铁锂电池的基本参数

1.2 试验设备

试验设备包括Well 公司的恒温箱（HLT404C）、NEWARE 公司的充放电综合性能测试设备（BTS-5V100A）及上位机，如图1所示。

图1 电池试验设备

1.3 试验内容

1.3.1 电池容量测试

定义SOCcut为截止SOC，即电池放电至截止电压时刻的SOC。电池容量测试采用恒温恒流放电，放电倍率分别为0.2C、0.5C、1C、2C、3C，从而得到一定温度和电流下电池的实际放电容量Qact，如式（1）所示。测试流程如表2 所示，最后得到不同温度和电流下电池SOCcut的MAP 图，如图2 所示。由图可知，温度越高且放电倍率越小，SOCcut越小。

图2 截止SOC的MAP

表2 电池容量测试过程

式中QN为锂离子电池的额定容量。

1.3.2 开路电压的测量

考虑到迟滞特性的影响，保证在测量放电开路电压（OCVd）的同时避免出现充电电流，反之亦然，所以单独设计试验测量放电开路电压（OCVd）和充电开路电压（OCVc），测量过程如表3 所示。考虑到磷酸铁锂电池电压平台的存在，得到平均开路电压（OCVa）关于温度和SOC的MAP，如图3（a）所示。验证磷酸铁锂电池存在明显的电压平台，在SOC较低时，OCVa急剧下降，相较于SOC，温度对OCVa的影响较小。

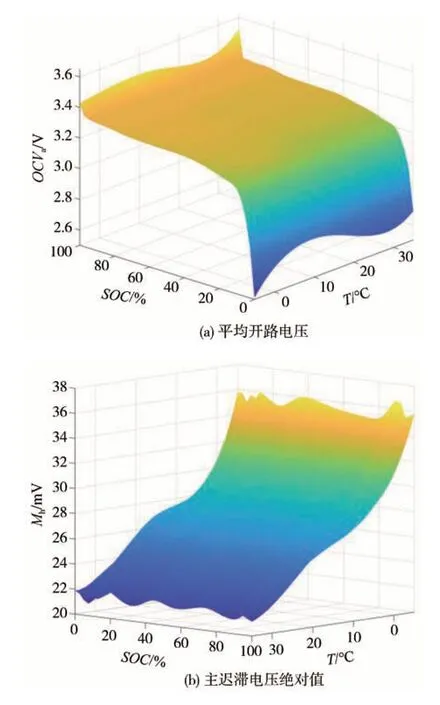
图3 电池电压的MAP图

表3 充放电开路电压的测量过程

定义充放电开路电压与平均开路电压的差值为主迟滞电压，其绝对值的MAP 如图3（b）所示。SOC对主迟滞电压的影响较小，而温度对主迟滞电压的影响较大。

2 考虑迟滞特性的电特性建模

2.1 电特性模型

作为集总参数模型的等效电路模型，凭借较少的参数反馈电池的静态和动态特性，且易推导出状态空间方程，具有计算量小、参数易辨识、精度较高等优点。本文考虑到工程的实际应用，综合评估模型的精度与复杂度，选用等效电路模型来模拟电池的电特性。

在诸多等效电路模型中，分数阶模型精度更高，但其参数过多，难以实现在线识别，且分数阶元件本质上缺乏明确的物理意义。RC 网络模型在工程应用中最为广泛，Thevenin 模型（1 阶RC 模型）能够较好地模拟电池极化，但无法区分电化学极化和浓度极化。为进一步提高模型估计精度，本文选用双极化模型（2阶RC 模型），如图4所示，其中Ri为欧姆内阻，RD1和RD2为极化内阻，CD1和CD2为极化电容，UD1和UD2为电池的极化电压，Ut为端电压。模型的状态空间方程如式（2）所示。

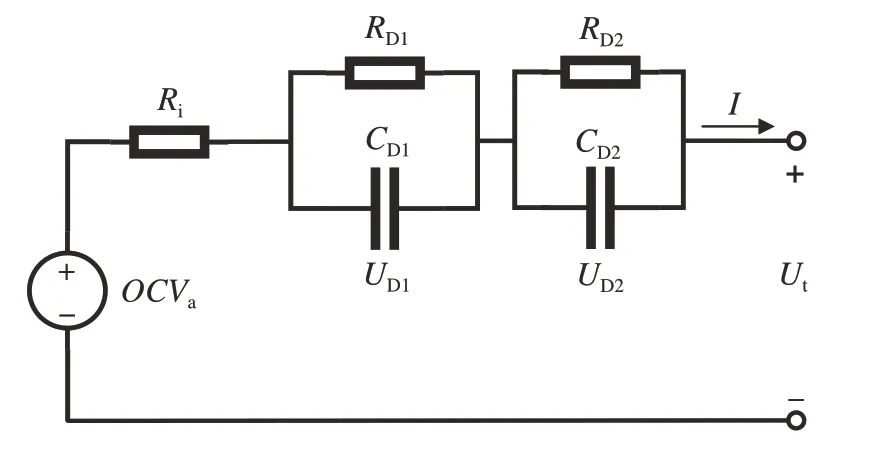
图4 2阶RC等效电路模型

2.2 迟滞特性建模

由于磷酸铁锂电池对迟滞特性较敏感，因此在模型中须考虑迟滞特性的因素。如图5 所示，电池从SOC=0%持续充电至SOC=100%，再从SOC=100%持续放电至SOC=0%，发现在OCV曲线之间形成一个开路电压区间。用Mh表示主迟滞电压，即相同SOC下，图中蓝色实线与绿色虚线之差，如式（3）所示。显然，主迟滞电压在充电时为正值，放电时为负值，两者互为相反数。在局部充放电区间内易形成迟滞回环，即图中红色实线，定义迟滞回环上的开路电压与平均开路电压OCVa之差为迟滞电压Uh，即相同SOC下，图中红色实线与绿色虚线的差值。综上所述，迟滞电压与电池充放电路径有关。一般将充放电平均开路电压作为开路电压的最终结果，而对于存在明显电压平台的磷酸铁锂电池，开路电压较小的波动会导致SOC的突变，影响SOC估计的准确性，因此不能忽视迟滞特性的影响。

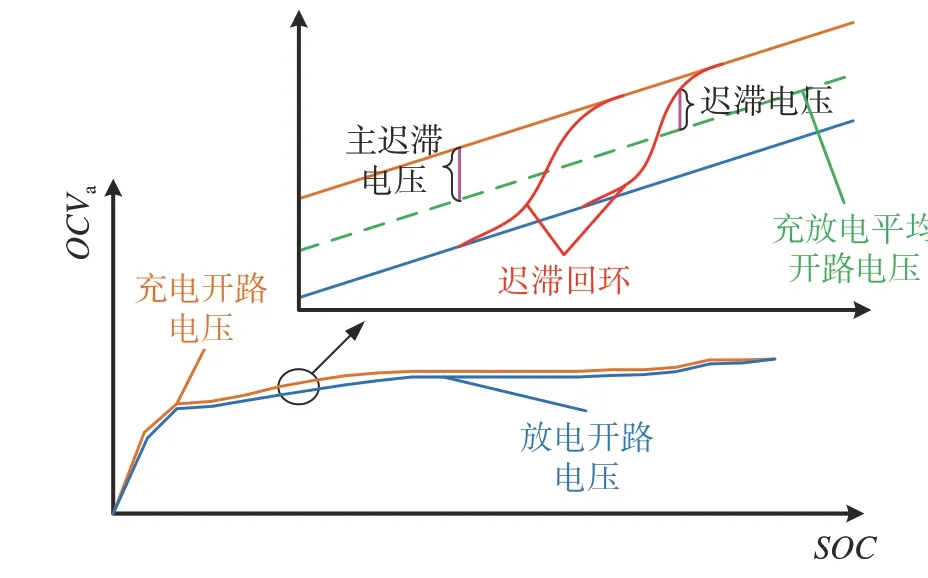
图5 主迟滞电压及迟滞电压示意图

考虑到工程应用的实时性和安全性，均衡复杂度与精度，本文将磷酸铁锂电池的迟滞特性描述为：越靠近迟滞回环的两端，迟滞电压的变化越小。基于此，得到迟滞电压与时间的函数关系，确定迟滞电压的微分方程如式（4）所示。

式中：sgn（·）表示符号函数；ε为迟滞系数。

式（4）中各参数进行等效并整理得

其中等效电阻Rh和等效电容Ch为

将式（5）离散化可得

综上所述，将迟滞模型与2 阶RC 等效电路模型联合，建议考虑迟滞特性的2 阶RC 等效电路模型，如图6所示。

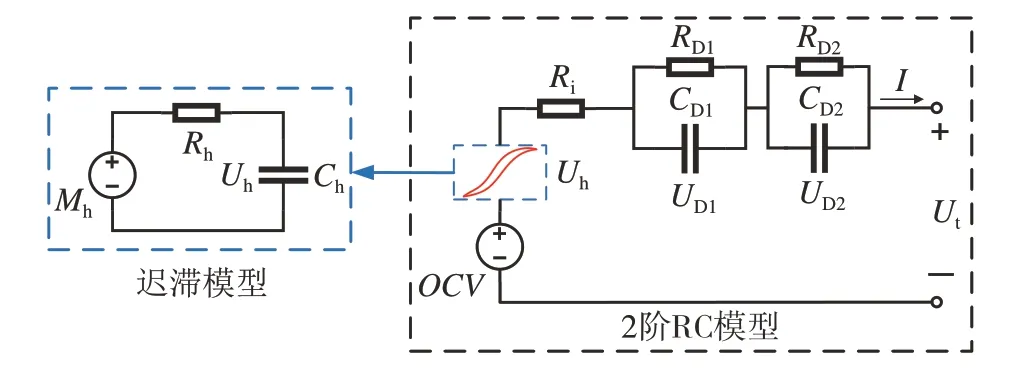
图6 考虑迟滞特性的2阶RC等效电路模型

模型总方程为

离散化后如式（9）所示：

2.3 在线参数辨识

通过模型的在线参数辨识，可提高电特性模型的环境温度自适应能力，更准确地模拟电池的电特性，进而提高电池SOC估计的精度。本文通过对电特性模型的状态空间表达式进行转化，采用带有遗忘因子的递推最小二乘法（forgetting factor recursive least square， FFRLS）完成在线参数辨识，转换过程如表4所示，得到FFRLS的标准式：

表4 带遗忘因子的递推最小二乘法的转化过程

式中：y为输出变量；Φ为数据变量矩阵；θ为参数变量矩阵，矩阵维度取决于待辨识参数的数目；eZw为零均值白噪声序列。

将电池模型的状态空间方程转换为FFRLS的标准 式后，采用式（11）所示的FFRLS递推式进行参数辨识。

式中：KFs为FFRLS 的增益因子；PFs为状态估计值的误差协方差矩阵；μ为遗忘因子，用于衡量旧数据与新数据的权重，调整信息总量中旧数据与新数据的占比，从而凸显新数据所起的作用，防止出现数据饱和现象，本文取为0.97；I为单位矩阵，这与电池的电特性模型参数的缓慢时变特性吻合。

电特性模型的输出变量、数据变量矩阵、参数变量矩阵和参数辨识矩阵依次如式（12）所示。参数变量矩阵与模型参数的表达式如式（13）所示，式中τ1、τ2为时间常数。

3 荷电状态的联合估计

基于模型的滤波算法及基于数据驱动的估计方法均为当前荷电状态估计的研究热点。尽管卡尔曼滤波算法能够输出较为稳定而精确的SOC，但必须假定其系统及测量噪声为高斯白噪声，噪声的初始化和不确定性问题导致SOC的准确估计复杂且鲁棒性不够理想，对系统的线性化过程也会进一步增大误差甚至导致结果发散。数据驱动方法虽然无须建立电池模型，但繁琐的超参数调节及训练数据的高质量要求严重制约其在工程化中的应用。本文提出了一种卡尔曼滤波和GRU 神经网络的荷电状态联合估计方法，不仅能够扩大噪声的选取范围，同时避免超参数的调节过程并降低训练样本的数量及质量要求。

3.1 基于自适应扩展卡尔曼滤波的SOC估计

噪声信息协方差匹配算法的提出使噪声统计特性随着估计结果的改变而自适应更新，在扩展卡尔曼滤波算法的基础上提出了自适应扩展卡尔曼滤波算法。SOC的离散定义如式（14）所示。

基于2.2节中建立的考虑迟滞特性的2阶RC等效电路模型，对其进行泰勒展开线性化得到模型的状态空间方程，如式（15）所示。

式中：m为当前时刻；x为系统状态变量；u为系统输入变量；ω为过程噪声；y为系统输出变量；υ为测量噪声；A为状态转移矩阵；B为输入增益矩阵；C为观测矩阵；D为补偿矩阵。

卡尔曼滤波系列算法的核心思想是对系统的状态做出方差最小的最优估计，将电池充放电的电流作为系统输入，其端电压为输出，通过端电压及SOC估计的误差实时地更新系统状态，从而获得最小方差的SOC估计结果。自适应扩展卡尔曼滤波的流程如图7 所示，其更新阶段公式如式（17）所示。

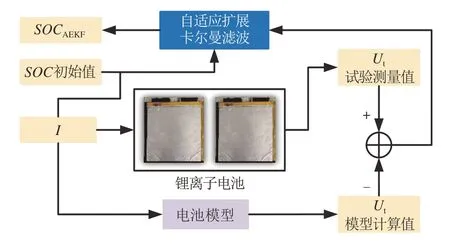
图7 自适应扩展卡尔曼滤波SOC估计流程

式中：-为系统状态变量的先验估计；+为系统状态变量的后验估计；P-为系统状态变量的先验误差协方差矩阵；P+为更新后的误差协方差矩阵；Q为系统过程噪声ω的协方差；R为系统测量噪声υ的协方差；K为卡尔曼滤波增益矩阵；I为单位矩阵。噪声的自适应更新过程如下：

式中：e为新息矩阵；H为开窗估计原理中的新息实时估计协方差函数；M为开窗的大小。

3.2 基于门控循环单元神经网络的SOC估计

基于数据驱动的SOC 估计方法无须搭建电池模型，避免了噪声明确过程繁琐及线性化损失精度的缺陷。循环神经网络能够有效地挖掘SOC 数据中的时序信息，不仅考虑了当前时间的输入，同时保留了过去一段时间内信息的记忆。但权重矩阵在循环过程中相乘会产生梯度消失或梯度爆炸等问题，这导致RNN 无法处理长时依赖问题，当输入序列较长时尤为明显。为此，有研究提出长短时记忆（long short-term memory， LSTM）神经网络，主要组成为三门（输入门、遗忘门和输出门）两记忆（长记忆和短记忆）结构，其迭代过程如式（19）所示。

式中：m表示时刻，I、F、O分别为输入门、遗忘门、输出门的输出；X为系统的输入；H为隐藏层状态；W为权重系数矩阵；b为偏置向量；C为记忆细胞状态；σ为sigmoid函数；tanh为双曲正切函数；⊙为元素乘法。

LSTM通过记忆细胞状态记录长期记忆信息，输入门控制当前时刻信息的输入量，遗忘门决定当前时刻保留的信息量，输出门控制记忆细胞中信息的输出量，在一定程度上克服RNN 无法解决的长时依赖问题，但LSTM 结构复杂，增加了网络训练的难度和时间。GRU 神经网络对LSTM 神经网络进行改进，将三输入两输出调整为两输入一输出，其中重置门Z决定了当前时刻新信息的输入量，更新门R控制当前时刻历史信息的保留量，如图8 所示。GRU神经网络通过重置门与更新门保存长时间序列信息，避免由于与当前时刻信息无关联或时间过长而遗忘的问题，其迭代过程如式（20）所示。

图8 GRU神经网络中隐藏状态的结构

式中R、Z分别为重置门和更新门的输出。

GRU 神经网络选择电流、电压和电池温度作为输入，电池SOC作为输出，采用基于梯度的优化算法进行模型训练。本文选用自适应矩估计（adaptive moment estimation， Adam）优化算法［27］，不同于通过单一且恒定学习率更新权重的随机梯度下降法，Adam 优化算法基于1阶梯度矩阵和2阶梯度矩阵的估计，针对不同的参数设计独立的自适应学习率，在内存占用较少的情况下加快训练速度。

3.3 联合卡尔曼滤波与GRU神经网络的SOC估计

噪声的初始值及修正对自适应扩展卡尔曼滤波算法的估计结果影响较大，且系统线性化的过程会产生误差。门控循环单元神经网络超参数的调节繁琐耗时。基于此，本文提出一种联合卡尔曼滤波算法和门控循环单元神经网络的SOC估计方法，以电流、电压及电池温度的实际值为输入，以AEKF 的估计结果为模型值，以GRU 神经网络的估计结果为测量值，通过卡尔曼滤波算法得到最终的SOC估计结果，并作为下一时刻AEKF 算法的输入，以此进行循环迭代，联合估计法的流程如图9 所示，相关参数表达式及迭代过程如式（21）～式（23）所示。针对系统的实际噪声为非高斯白噪声，抑或噪声的自适应更新规则不适等问题，联合估计方法能够通过GRU 神经网络对AEKF的估计结果进行修正，同时AEKF算法的引入能够适当降低GRU 神经网络估计精度的要求，从而减少了超参数调节的时间和训练成本。

式中：SOCAEKF为通过AEKF 算法估计得到的SOC；SOCGRU为通过GRU 神经网络估计得到的SOC；SOCKF为联合估计方法得到的SOC。

4 精度验证

4.1 工况试验

工况试验用于检验电池模型的精度，常用的工况包括动态应力测试（dynamic stress test， DST）和美国联邦城市驾驶工况（federal urban driving schedule，FUDS），为更直观且高效地调整并输入工况信息，本文将传统工况的输入由功率修改为电流，删除了电流为0的部分，并命名为IDST 和IFUDS。此外，分别在25 与-5 ℃以及变环境温度下设置工况试验。变环境温度工况指的是随时间而改变恒温箱的温度，用于模拟实车的行驶环境，工况的电流输入及恒温箱温度（即环境温度Ta）变化如图10所示。

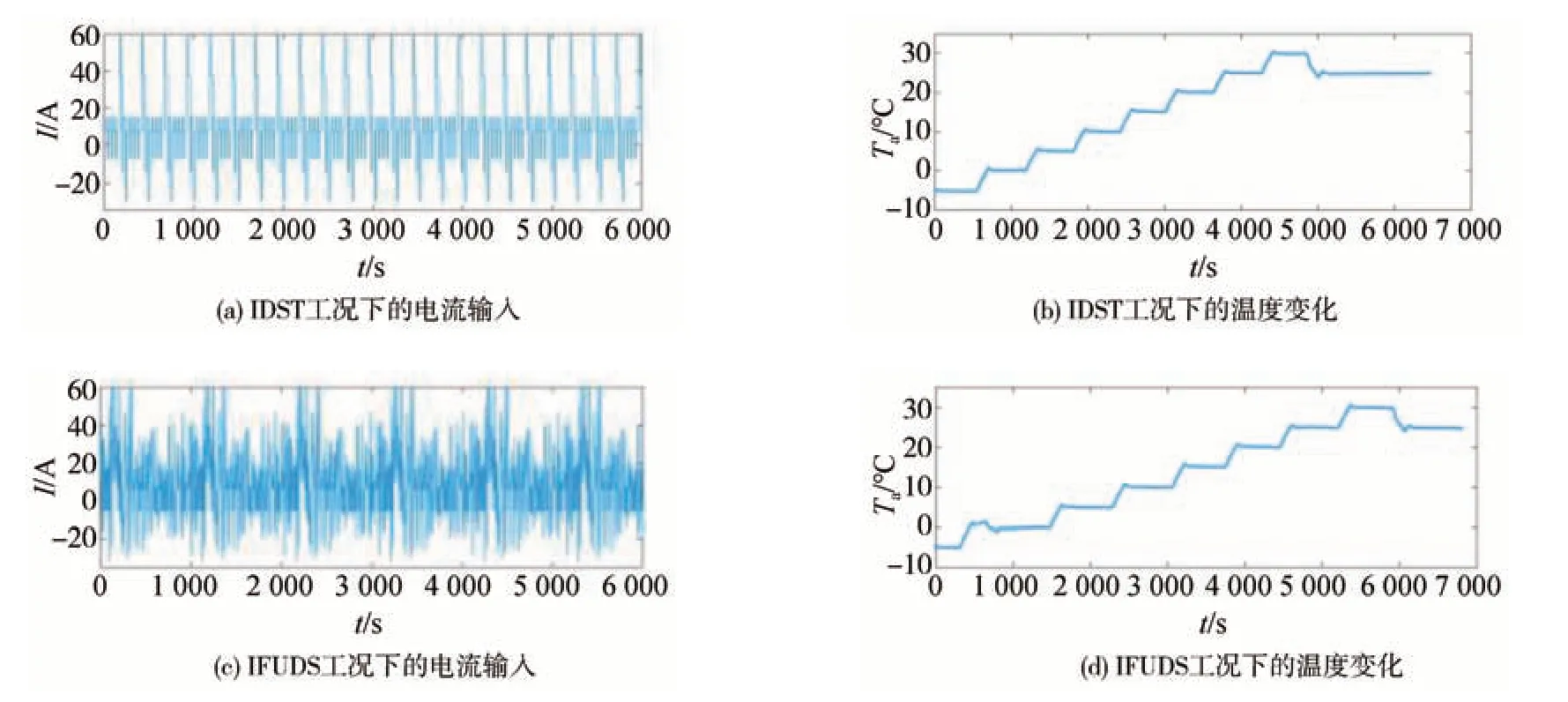
图10 工况数据

4.2 在线参数辨识的精度验证

在环境温度25 ℃的IDST和IFUDS两种工况下，对完成在线参数辨识的考虑迟滞特性的电特性模型的精度进行验证，并将模型的计算值与真实值进行比较，如图11和图12所示。

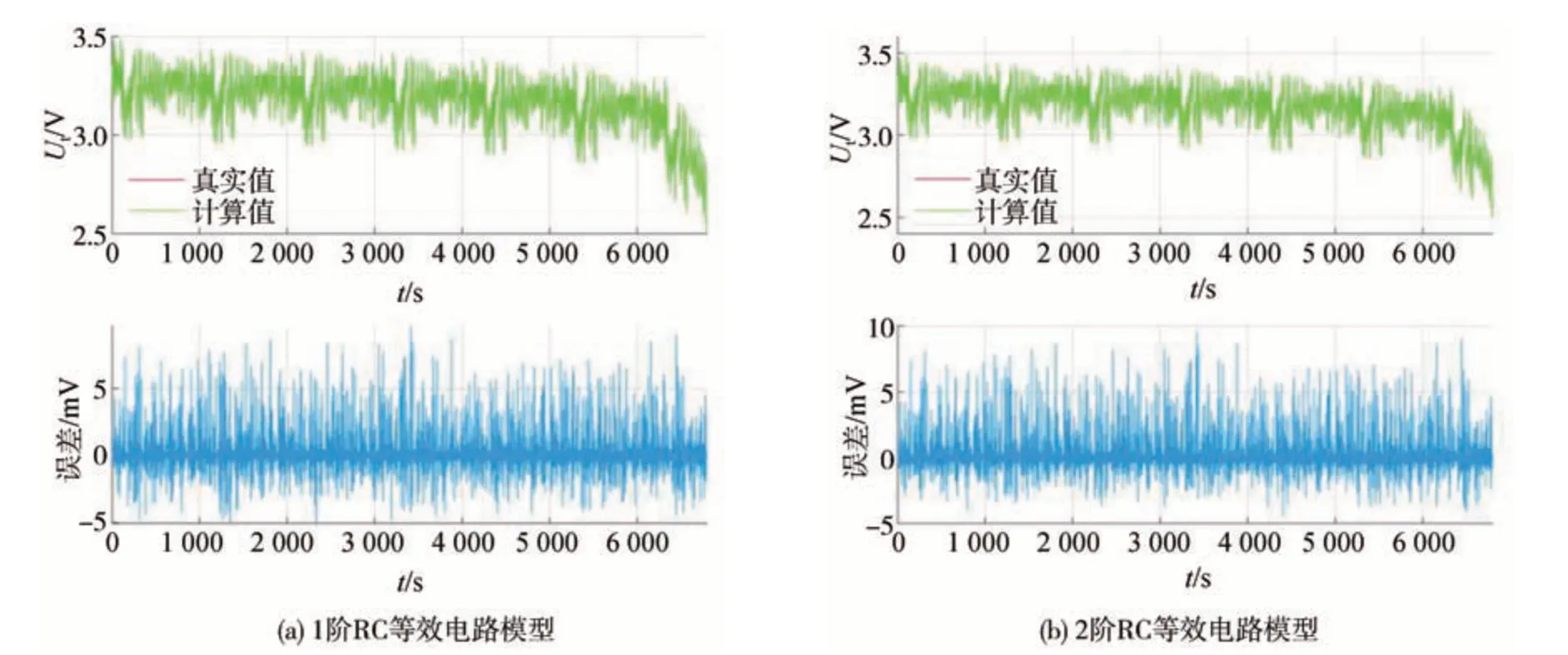
图11 25 ℃ IDST工况下考虑迟滞特性模型的端电压与误差

图12 25 ℃ IFUDS工况下考虑迟滞特性模型的端电压与误差

通过最大绝对误差和均方根误差两种评价指标与未考虑迟滞特性的电特性模型的计算结果进行对比，如表5所示。考虑迟滞特性的电特性模型在两种工况下的RMSE均小于0.5 mV，MAE保持在10 mV 以内，且由于IDST 工况的波动频率较低，因此其相应的RMSE和MAE都要小于IFUDS工况。而未考虑迟滞特性的电特性模型对应的端电压误差均大于考虑迟滞特性的误差，证明在建模时考虑迟滞特性的重要性。此外，2阶RC等效电路模型的RMSE和MAE均大于1阶RC 等效电路模型对应的RMSE和MAE，证明2 阶RC等效电路模型的精度高于1阶RC等效电路模型。

表5 25 ℃两种工况下是否考虑迟滞特性的电特性模型精度对比

考虑到IFUDS 工况的波动频率较大，分别设置-5 ℃及变环境温度的IFUDS工况，对在线参数辨识下考虑迟滞特性的电特性模型精度进行验证，结果如图13 和图14 所示，端电压的精度误差如表6 所示。尽管-5 ℃和变环境温度下模型的误差有所增加，但2阶RC等效电路模型的RMSE仍保持在0.9 mV以下，MAE均小于20 mV，说明在线参数辨识下，考虑迟滞特性的2阶RC等效电路模型具有良好的鲁棒性。

图13 -5 ℃ IFUDS工况下考虑迟滞特性模型的端电压与误差

图14 变温 IFUDS工况下考虑迟滞特性模型的端电压与误差

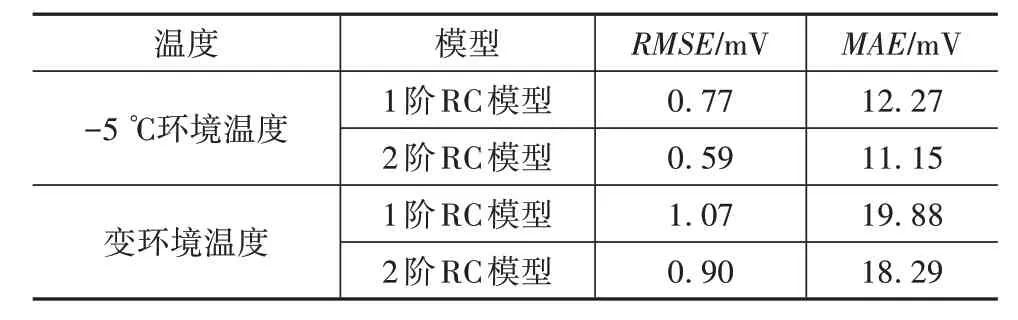
表6 -5 ℃和变环境温度IFUDS工况下考虑迟滞特性的电特性模型精度对比

4.3 SOC估计精度验证

考虑到温度对OCVa的影响较小，因此选取25 ℃下OCVa与SOC的关系式作为最终结果。基于多项式拟合函数得到25 ℃下OCVa与SOC的关系，如图15所示，多项式的各项系数如表7所示，dOCVa/dSOC与SOC的8次方关系式如式（24）所示。

图15 25 ℃下OCVa与SOC的拟合关系

表7 25 ℃下OCVa与SOC多项式的各项系数

针对GRU 神经网络，分别选用不同的工况进行训练和估计。在训练前通过最大最小标准化对输入的电流、电压及温度数据进行归一化处理，如式（25）所示。卡尔曼滤波将AEKF算法与GRU神经网络得到的SOC估计结果相结合，将两者的误差过滤后获得最优的SOC估计，进而避免了GRU 神经网络繁琐的超参数调节及AEKF噪声的初始化和更新过程。

考虑到试验设备的测量精度及采样间隔为0.1 s，假设试验设备测量的电流值为真实值，并设置SOC的初始值为100%。但实车上电流传感器精度有限且采样间隔较大，因此为电流的真实值添加一个始终为正或为负的偏差噪声，用于模拟实车驾驶工况下电流的测量值。

4.3.1 常温环境下的SOC估计精度验证

分别在环境温度25 ℃的IDST和IFUDS工况下，对经典的安时积分法、GRU 神经网络、AEKF 算法及本文提出的联合估计法进行验证，结果如图16 所示，均方根误差和最大绝对误差如表8所示。

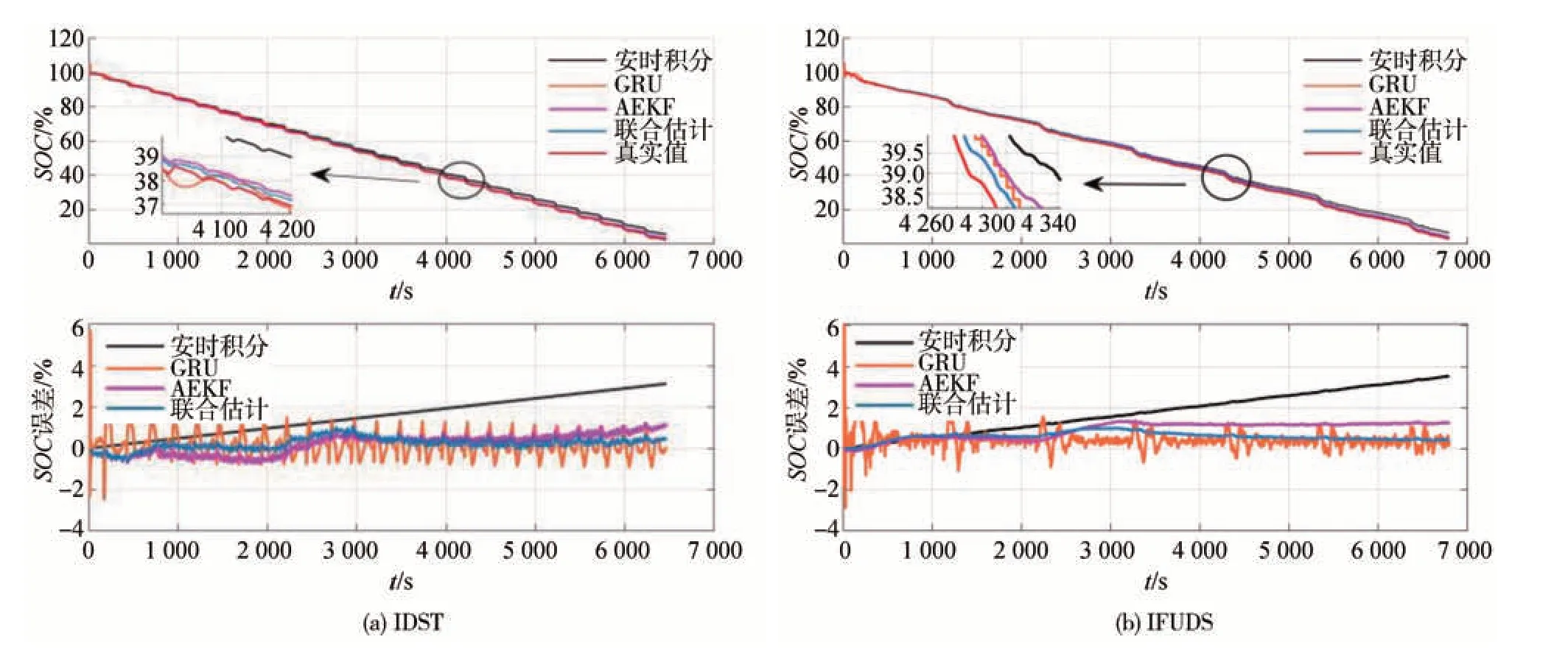
图16 25 ℃工况下SOC估计结果与误差对比

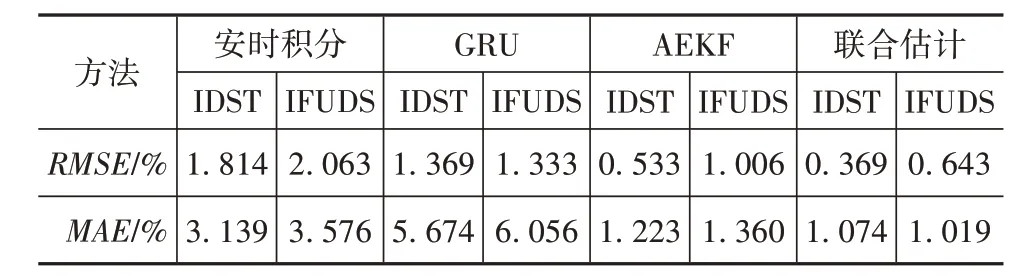
表8 25 ℃ IDST和IFUDS工况下的SOC估计精度

通过验证可知，联合估计法的SOC估计精度高于安时积分法、GRU 神经网络和AEKF 算法。安时积分法的SOC估计误差主要源于传感器带来的偏移噪声，且随着时间而逐步累积。GRU 神经网络的初始估计精度较差，而后逐渐收敛，但波动较大，且学习率及隐藏层的维度等超参数的调节增加了大量的时间成本。由于电流真实值中偏移噪声及1 阶泰勒公式展开时线性化过程的存在，AEKF 算法的SOC估计结果难以较好收敛。联合估计法的SOC估计误差平稳于零值附近，两种工况下SOC估计结果的RMSE最大值仅有0.64%，证明联合估计法具有较高的SOC估计精度。

为验证本文提出的SOC联合估计法的自回归能力，将初始的SOC输入为50%（实际为100%），试验结果如图17所示。SOC的估计结果能够在50 s内实现修正，证明联合估计法具有较好的自校正能力。

图17 初始SOC为50%、SOC联合估计法的估计结果

4.3.2 低温及变温环境下的SOC估计精度验证

在-5 ℃和变温环境的IFUDS 工况下进行验证，估计结果如图18所示，RMSE和MAE如表9所示。

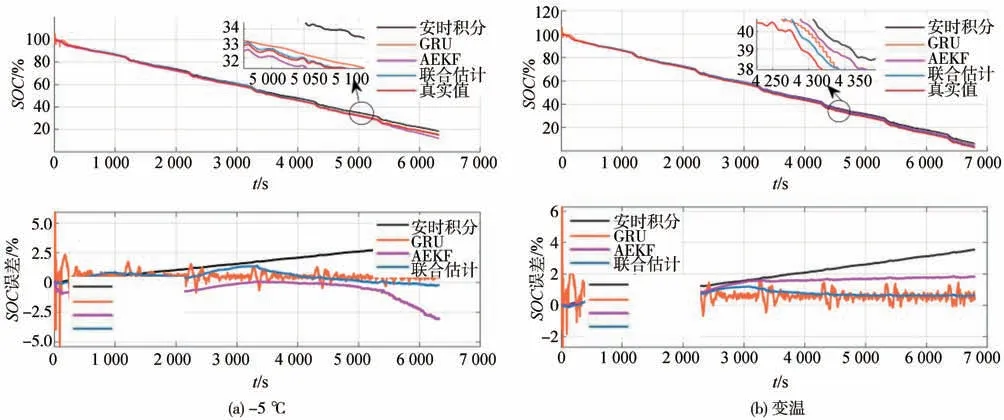
图18 IFUDS工况下SOC估计结果与误差对比

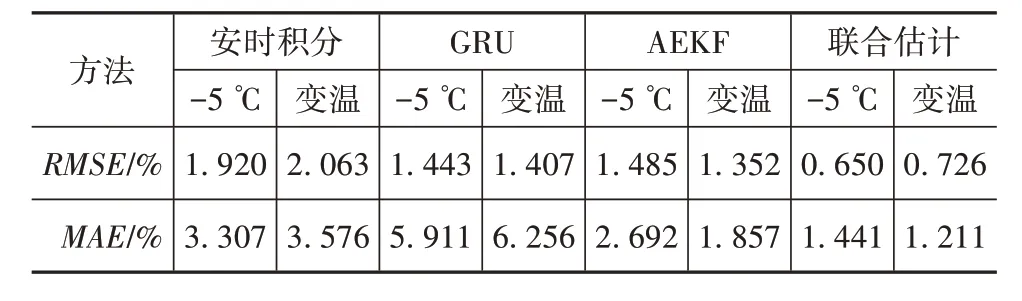
表9 -5 ℃和变温环境IFUDS工况下的SOC估计精度

经过验证可知，-5 ℃和变温环境下各方法的估计误差略大于常温环境，但联合估计法的SOC估计精度仍高于安时积分法、GRU 神经网络和AEKF 算法。由于噪声自适应更新及低温环境对电池模型精度的影响，在低温及变温环境下AEKF 算法的SOC估计精度较差，甚至出现估计结果发散的趋势。相较于安时积分法、GRU 神经网络和AEKF 算法，联合估计法在所有工况下均保持较为精确而稳定的SOC估计精度，且具有更强的鲁棒性。

5 结论

考虑到迟滞特性对磷酸铁锂电池的影响较大，本文基于迟滞特性的分布规律修正平均开路电压OCVa-SOC曲线，提出了更为精确的考虑迟滞特性的锂离子电池2 阶RC 等效电路模型。然后利用带有遗忘因子的递推最小二乘法对电池模型参数进行在线辨识。

为提高锂离子电池SOC的估计精度及收敛速度，本文提出一种联合GRU 神经网络和AEKF 的SOC估计法，将AEKF 的估计结果作为模型值，将GRU 神经网络的估计结果作为测量值，通过KF 获得最终的SOC估计结果，并作为下一时刻AEKF 的输入，以此迭代循环。联合估计法不仅克服了AEKF 算法线性化过程造成的误差及噪声自适应更新不适等问题，同时避免了GRU 神经网络超参数调节繁琐耗时的缺点。

最后在常温、低温及变温环境的IDST 和IFUDS动态工况下进行对比验证。结果表明：25 ℃环境下，考虑迟滞特性的模型对端电压预测及联合估计法对SOC估计的RMSE分别在0.5 mV 和0.64%以内；-5 ℃及变温环境下，端电压预测及SOC估计的RMSE分别在0.9 mV 和0.72%以内。说明考虑迟滞特性的模型及联合估计法具有良好的精度和鲁棒性，为后续电池能量状态、功率状态等重要性能指标的精确预测奠定了基础。