不同乐器结构音色的识别研究
汪 洋
(沈阳音乐学院,沈阳 110000)
0 引言
音色反映了声音的特色和品质。不同乐器因材料和结构不同,会有不同的音色,从而使乐器发出不同品质的声音,这成就了乐器独一无二的艺术特征。音色识别是辨别乐器的重要手段,但传统乐器音色识别主要依靠专业人员,存在效率低、辨别准确率不高等问题,因此如何采用更为智能化的手段进行识别成为当前研究的热点。近年来,随着人工智能技术的发展,乐器音色的识别成为智能识别领域研究的热点。目前,国内外对乐器音色的识别主要通过倒谱特征结合深度学习方法进行,如赵庆磊等[1]融合倒谱特征和图像领域特征,采用ResNet34变体网络对融合特征进行学习,实现了乐器音色的识别,且识别准确率达93.3%;李峰等[2]利用粒子群优化算法(particle swarm optimization,PSO)改进BP神经网络,构建PSO-BP神经网络识别模型,实现了对中国民族乐器的识别;李子晋等[3]针对中国民族复音音乐的乐器识别难度高的问题,提出一种基于卷积循环神经网络(CRNN)的分类识别方法,实现了对10种中国民族乐器的识别。上述研究积累了丰富经验,但谢黛安[4]认为现有乐器识别的准确率还可进一步提高。因此,本文基于去噪自编码器(Denoising Autoencoder,DA)和受限玻尔兹曼机(Restricted Boltzmann Machines,RBM)在特征提取中的优势,提出一种DA-RBM模型的不同乐器结构音色分类识别方法。
1 基本算法
1.1 去噪自编码器
去噪自编码器是在传统自编码器的基础上,通过添加噪声,然后利用含噪声的损坏样本重构不含噪声的原始样本的一种神经网络,从而提取到原始数据更深层次的表达性特征,基本结构如图1所示[5]。
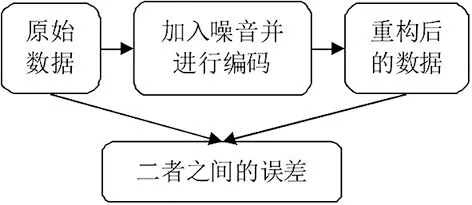
图1 去噪自编码器结构
去噪自编码器的目的是重构输入,以使网络可更好学习到输入特征。通俗来说,去噪自编码器的目的是使误差函数η最小。因此,设原始数据为M,重构后的数据为N,则去噪自编码器的误差函数η的表达式为:
1.2 受限玻尔兹曼机
受限玻尔兹曼机是利用输入数据学习概率分布的一种随机生成神经网络,其结构如图2所示。该网络是一种由可视层和隐藏层构成的无向图模型。

图2 RBM模型结构
设受限玻尔兹曼机的可视层和隐藏层神经元数量分别为n和m个,对应的状态表示为V和H,则对于已知状态(v,h),RBM的负能量函数表示为[6]:
式(2)中,vi、hj分别表示可视层节点i和隐藏层节点j的状态;θ={Wij,bj,ai}为RBM的参数;Wij表示节点i到j的实数权值;bj表示节点j的偏置;ai表示节点i的偏置。若给定参数,基于能量函数E(v,h|θ),可抽样得到状态(v,h)的联合概率分布函数为:

根据RBM模型结构可知,当可视层神经元状态已知时,隐藏层的神经元状态是相互独立的。因此,RBM模型的激活概率可用式(4)和式(5)表示:
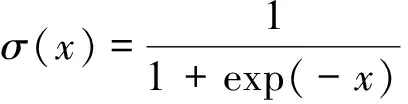
2 基于DA-RBM的不同乐器结构音色识别模型构建
2.1 网络结构设计
为更好地提取音色的高级特征,结合去噪自编码器(DA)和受限玻尔兹曼机(RBM)的特点,将不同乐器结构音色识别模型构建为图3所示。模型由两层DA和两层RBM组成,负责提取不同乐器结构音色的听觉谱图。考虑到DA网络和RBM网络均为特征提取网络,不能进行分类与识别,因此在DA网络和RBM网络后连接1层softmax分类层,从而用于乐器音色听觉谱图的分类与识别,并输出识别结果。

图3 基于DA-RBM的不同乐器结构音色识别网络结构
由图3可知,以听觉谱图作为深度学习网络的输入,以不同乐器结构的音色识别结果作为输出。具体流程如下:
(1)样本集制作。收集整理不同乐器结构的音色音频,并将所有样本生成听觉谱图。然后结合经验按7∶3的比例将听觉谱图划分为训练集和测试集,用于DA-RBM模型的训练与测试;
(2)确定DA-RBM各层网络节点数。由于听觉图谱的滤波器为128组,因此生成的听觉谱图为128*100的矩阵,故将DA-RBM模型的输入节点数为12800。考虑到第一层去噪自编码器隐藏层节点数直接关系到模型性能,因此通过试验法设置第二层DA隐藏层节点数和第一层RBM和第二层RBM隐藏层节点数。最后,根据分类识别结果设置softmax分类层节点数;
(3)确定网络激活函数及参数。采用relu函数降低网络梯度下降复杂度,并以10%的概率对网络显层节点进行失活,梯度下降概率设为0.002,学习速率设为0.01;
(4)网络微调。采用adam优化算法自适应调整网络梯度下降速率,设置步长为0.001,并以50%的概率对每层节点进行随机失活;
(5)基于上述训练的模型,将测试集输入模型,得不同乐器结构音色的分类识别结果。
2.2 听觉谱图的特征提取
由于乐器结构不同,其谐波分量也不相同,因此选用听觉谱图对不同乐器特征进行提取。听觉谱图由耳蜗模型通过频率分解得到,而耳蜗模型包括基底膜和外毛细胞模型[7-8]。其中基底膜模型是利用Gammatone带通滤波器将乐音分解为多个不同中心频率的通道,每个中心频率覆盖8.6个倍频程。通过基底膜模型的乐音信号可表示为[9]:
y1(t;s)=m(t)*th(t;s)
(6)
式中,下标*t表示对时间t进行卷积;s表示滤波器组的中心频率;h(t;s)表示Gammatone带通滤波器脉冲响应,可通过式(7)计算:
h(t;s)=ctn-1e-2nbtcos(2πst+φ),t>0
(7)
式中,c=1为调节比例常数;n=4表示滤波器级数;b=1表示衰减系数;φ表示相位。
外毛细胞模型负责对滤波器组通道进行差分,并使用积分窗模拟快速变化的信号。最终得听觉谱图,表示为[10]:
y2(t;s)=∂sy1(t;s)*tμ(t;τ)
(8)
式中,∂s表示差分,μ(t;τ)=e-t/τε(t),τ为时间常数。
3 软件和平台实验
3.1 实验环境搭建
本实验基于Tensorflow深度学习框架搭建DA-RBM模型,并在Windows10操作系统上进行仿真验证。系统配置Intel(R)Xeon(R)Gold6152 CPU,GTX1050(4G)显卡。
3.2 数据来源及预处理
本次实验选用爱荷华大学电子音乐实验中心的IOWA音响库作为不同乐器结构音色分类识别的样本。该音响库包括弦大号、钢琴、吉他、大提琴、小提琴、萨克斯管、木琴、长笛、低音管9种乐器,均为44.1 KHz频率采集的16 bit单声道数字信号[11]。考虑到不同乐器样本量不同,为均衡样本量,从每种乐器中任意选取500个样本作为实验样本,共4500个样本。
最后,将选取的样本按照7∶3比例划分为训练集和测试集用于本文所提DA-RBM模型训练与测试。
3.3 评价指标
本次实验选用准确率(acc)、F值和平均训练时间作为性能评估指标。其中,准确率和F值的计算方法如下[12-13]:
式(9)中,TP、TN分别表示真正例和真负例;FP、FN分别表示假正例和假负例。式(10)中,P表示精确度,可通过式(11)计算;R表示召回率,可通过式(12)计算[14];α=1表示调和因子。
3.4 参数设置与优化
设本文所提DA-RBM模型输入层节点数为12800,第二层DA的隐藏层节点数和两层RBM隐藏层节点数分别设置为5000、1000、200,softmax层输出节点数设为9,学习率设置为0.01,梯度下降概率设为0.002,采用adam优化算法对梯度下降速率进行自适应调整,步长设置为0.001。
由于第一层DA负责提取听觉谱图特征,直接影响到所提DA-RBM模型的识别效果。因此,第一层DA的隐藏层节点数选择十分重要。为选取第一层DA的隐藏层节点数,通过设置不同隐藏层节点数量,并观察模型的识别准确率,从而确定最佳隐藏层节点数。第一层DA不同隐藏层节点数下的识别准确率如图4所示。由图4可知,随着节点数与输入节点数倍数增加,DA-RBM模型的识别准确率先上升后下降。当第一层DA节点数是输入节点数2倍时,DA-RBM模型的识别准确率最高,达到97.50%。因此,将第一层DA的隐藏层节点数设为输入节点数的2倍,即25600。

图4 第一层DA不同隐藏层节点设置下的识别准确率
3.5 结果与分析
3.5.1模型验证
(1)性能验证
为验证DA-RBM模型的有效性,利用实验数据集对DA-RBM模型中层2到层4进行训练。图5为DA-RBM模型各层的训练过程。由图5可知,随着DA-RBM模型迭代进行,各层误分率逐渐减小,且下降速率较快;当迭代50次后,各层误分率达到最小值,说明迭代50次可确保DA-RBM模型参数达到局部最优。由此说明,所提DA-RBM模型通过训练可快速收敛,模型有效。利用DA-RBM模型可有效抽象表示不同乐器结构听觉谱图中音色的高级时频。
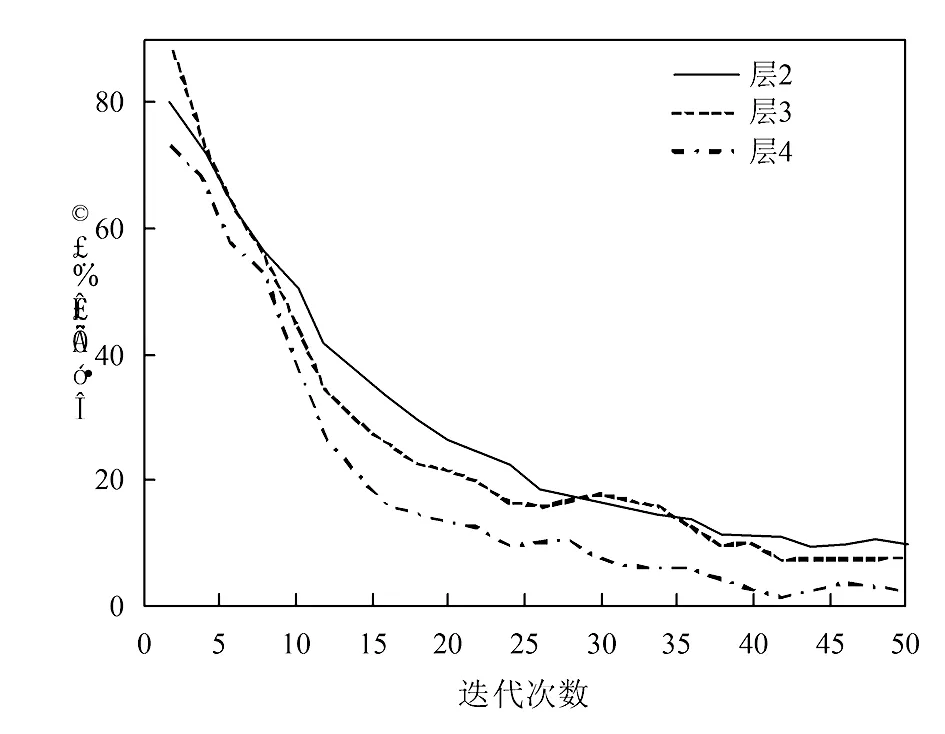
图5 DA-RBM模型各层训练过程
为分析所提DA-RBM模型对特征提取的有效性,利用线性判别分析的方法将模型每层节点的输出投影到二维平面,得到本研究提出的图3深度学习从第一层DA到第四层RBM的投影如图6所示。由图6可知,所提DA-RBM模型对样本的分离程度逐渐增强,说明所提DA-RBM模型可有效逐层提取特征,足以证明所提DA-RBM模型具有一定的合理性和正确性。
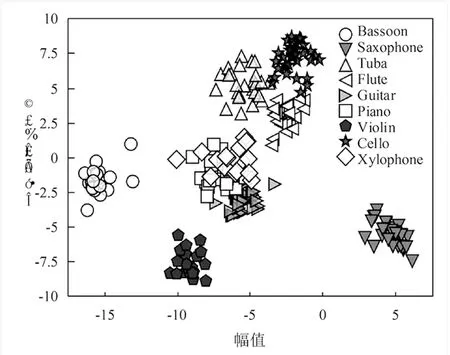
a.第一层投影
(2)输入特征对DA-RBM模型识别率的影响
为验证所提DA-RBM模型选用听觉谱图作为输入特征的有效性,对比了以听觉谱图和语谱图以及MFCC作为所提DA-RBM模型输入特征时,模型的识别混淆矩阵,结果如图7所示。由图7可知,基于语谱图特征输入的DA-RBM模型平均识别准确率为96%,基于MFCC特征输入的DA-RBM模型平均识别准确率为78%,基于听觉谱图特征输入的DA-RBM模型平均识别准确率为97%。由此说明,相较于基于语谱图和MFCC作为模型输入时,采用听觉谱图作为模型输入的准确率更高。分析其原因,是语谱图频率为线性,而人耳对乐器结构音色的频率感知为非线性,因此语谱图特征增加了特征的冗余信息,导致乐器分类识别准确率达不到理想效果;MFCC的本质是一种倒谱特征,对共振腔结构的乐器容易出现错分,因此其识别准确率较低。由此说明,所提DA-RBM模型选用听觉谱图作为输入特征,具有一定的有效性和合理性。
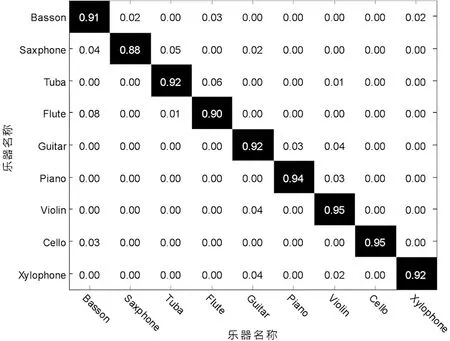
(a)听觉谱图输入的混淆矩阵
3.5.2模型对比
对比所提DA-RBM模型与双层DA网络堆叠的SDA+softmax模型和双层RBM+softmax堆叠的DBN模型的识别优势,结果如表1所示。由表1可知,所提的DA-RBM模型在准确率指标上的表现均优于SDA模型和DBN模型,识别准确率达到97.18%,说明DA-RBM模型对不同乐器结构音色的识别准确率更高,具有一定的有效性和优越性。

表1 不同模型性能对比
对比所提DA-RBM模型与多尺度时频调制和基于CNN识别的准确率和训练时长,结果如表2所示。由表2可知,所提DA-RBM模型的平均识别准确率相较于对比的模型高5.49%和1.30%;在训练总时长方面,所提DA-RBM模型与多尺度时频调制和CNN的训练总时长差异较小,分别为2.57 s、2.34 s、2.86 s。由此说明,所提DA-RBM模型在确保训练时长前提下,可有效提升了识别的准确率。

表2 不同模型分类识别性能对比
4 结论
综上,所提的DA-RBM的不同乐器结构音色识别方法,在对大号、钢琴、吉他等不同乐器结构的音色识别中,平均识别准确率达到97.18%,平均训练时长2.57 s,在识别准确率上具有一定的优势。由此表明本研究构建的DA-RBM的识别模型可行,对不同乐器结构音色识别具有一定的有效性和优越性。

