改进的Ambrosio-Tortorelli模型及其图像分割应用

范 琴,胡 华

(宁夏大学 数学统计学院, 宁夏 银川 750021)

0 引言

Mumford-Shah模型是偏微分方程图像处理模型的典型代表之一[1],它以泛函变分、偏微分方程等数学原理和方法为基础,将图像分割问题转化为泛函极小化问题,具有很强的几何物理意义,能够克服传统图像分割方法的许多弊端,吸引了众多学者研究.早期泛函建立在C1类函数空间上,数值求解局限性较大,Giorgi E D等[2]将其放宽到特殊有界变差(SBV)函数空间上,提出了Mumford-Shah泛函的弱形式;在此基础上,Ambrosio L等[3]利用椭圆泛函近似弱形式中的几何项,得到Ambrosio-Tortorelli模型,使得模型数值求解容易实现.

近年来,不少学者对Ambrosio-Tortorelli模型进行了深入研究,主要集中在模型的数值求解研究和改进研究两个方面.关于模型数值求解,部分学者[4-6]考虑采用有限差分和有限分方法进行求解,通过改进网格剖分方法,有效解决了数值求解过程中产生的各向异性阻碍和边界图像过厚且模糊的问题;Foare M等[7-8]用离散微积分框架表示了AT泛函的离散微积分公式,该方法对于复杂的拓扑框架,也能清晰地表示边界,并且对噪声具有较好的稳定性.关于模型改进,Trieu H,Foare M等[9]推导出PALM和SL-PAM两种迭代格式来求解Ambrosio-Tortorelli泛函,并提出了一种多分辨率的网格搜索策略进行参数选取,数值实验表明PALM格式具有更优的图像分割效果,但SL-PAM格式由于计算成本过大,导致时间成本较大、分割效果相对较差;Burger M等[10]分别用Laplacian和Hessian二阶边缘项代替模型中的一阶惩罚边缘项,提出了两个改进模型,该方法具有边缘轮廓更平滑清晰、算法迭代次数显著减少、收敛更优的特点.

本文在Ambrosio-Tortorelli模型基础上,考虑其图像分割应用中边缘检测能力不足的问题,在确保模型解的存在性等良好性质前提下,对模型的边缘惩罚项进行改进,提出了一种新的图像边缘测度的逼近形式,采用变分法、梯度下降法和有限差分法等设计了有效的数值求解算法,通过数值实验实现了图像弱边缘检测能力的提高.

1 Ambrosio-Tortorelli模型

Mumford-Shah模型是由Mumford D等[11]在1989年针对计算机视觉中的图像分割问题提出的解决方法.该模型如下:

MS(u,Γ)=∬Ω(u-g)2dxdy+
λ∬ΩΓ|∇u|2dxdy+α|Γ|.

(1)

其中:g是要进行处理的原始图像,g∈L∞(Ω);Ω为有界开集合,Ω⊂R2;u∈C1(ΩΓ),u是对图像g的逼近光滑图像;Γ是图像g中的不连续点集;|Γ|代表组成Γ的弧的总长度;λ,α>0是调节参数.

求解Mumford-Shah模型就是要找出最优的u和Γ,使得能量泛函MS值最小.Mumford-Shah模型由3项组成:第一项是保真项,表示逼近光滑图像u与输入图像g的近似程度;第二项是平滑项,强调u在区域ΩΓ上尽量平滑;第三项是几何测度项,确保边缘不致填满整幅图像,即要求边界曲线Γ尽可能光滑.

Mumford D和Shah J提出的泛函建立在C1类函数空间上,且其中的几何项是非下半连续的,使得该泛函求解十分困难.Giorgi E D等[2]在有界变差(BV)函数空间的基础上,发展了特殊有界变差(SBV)函数空间,将原泛函放宽到特殊有界变差函数空间上,并将Γ集用u的不连续集Su替代,得到了Mumford-Shah模型的弱形式:

MSw(u)=∬Ω(u-g)2dxdy+
λ∬Ω|∇u|2dxdy+αH1(Su).

(2)

其中,u∈SBV.

虽然Giorgi E D等[12]证明了Mumford-Shah泛函在SBV空间下的弱形式的解的存在性,但因为其中几何项的存在使得弱泛函是不可微的,从而无法推导得出弱泛函对应的欧拉-拉格朗日方程,所以该弱泛函的数值求解仍然是十分复杂的.Ambrosio L和Tortorelli V M[3]对式(2)进行了改进,在Γ收敛相关理论基础上,利用辅助函数

Mε(v)=
∬Ω(ε|∇v|2+W(v)/4ε)dxdy,

近似式(2)中的几何项H1(Su),其中W(v)=1-v2,从而得到了Mumford-Shah模型的逼近形式—Ambrosio-Tortorelli模型:

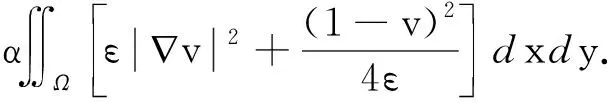
(3)

Maso G D等[13]证明了泛函ATε扩展到W1,2(Ω)×W1,2(Ω)之外的+∞,在ε→0+时,Γ收敛到泛函MSw.在Ambrosio-Tortorelli模型中,求解对象u仍然是分割后的平滑图像,但另一求解对象v不再是原泛函中的边缘Γ,而是输入图像g的边缘图像,所有积分都定义在同一二维区域Ω,并用椭圆泛函Mε(v)近似不连续集Su的Hausdorff一维测度,使得数值求解更容易实现.

2 改进的Ambrosio-Tortorelli模型

Ambrosio-Tortorelli模型可利用变分法、梯度下降法和有限差分法等方法直接进行数值求解[14],利用数值求解结果进行数值实验,可以发现,该模型对图像弱边缘检测能力较弱,易导致分割后的边界图像v产生边缘信息弱化现象.

为克服这一缺点,本节对Ambrosio-Tortorelli模型进行了改进,在保证模型解的存在性等良好性质前提下,对辅助函数Mε(v)中W(v)项进行修改,构建了新的图像边缘测度逼近项.从原模型W1(v)=(1-v)2的图像特征出发,寻求与其具有类似图像特征的W(v),最终确定将其修改为W2(v)=e-5v2.

W2(v)和Vr2(v)函数对比如图1所示,从图中可发现,在[0,1]区间内,W1(v)与W2(v)具有类似的性质:图像都呈现单调递减趋势;图像都经过点(0,1);W1(v)函数图像经过点(1,0),W2(v)函数曲线无限趋近于点(1,0).

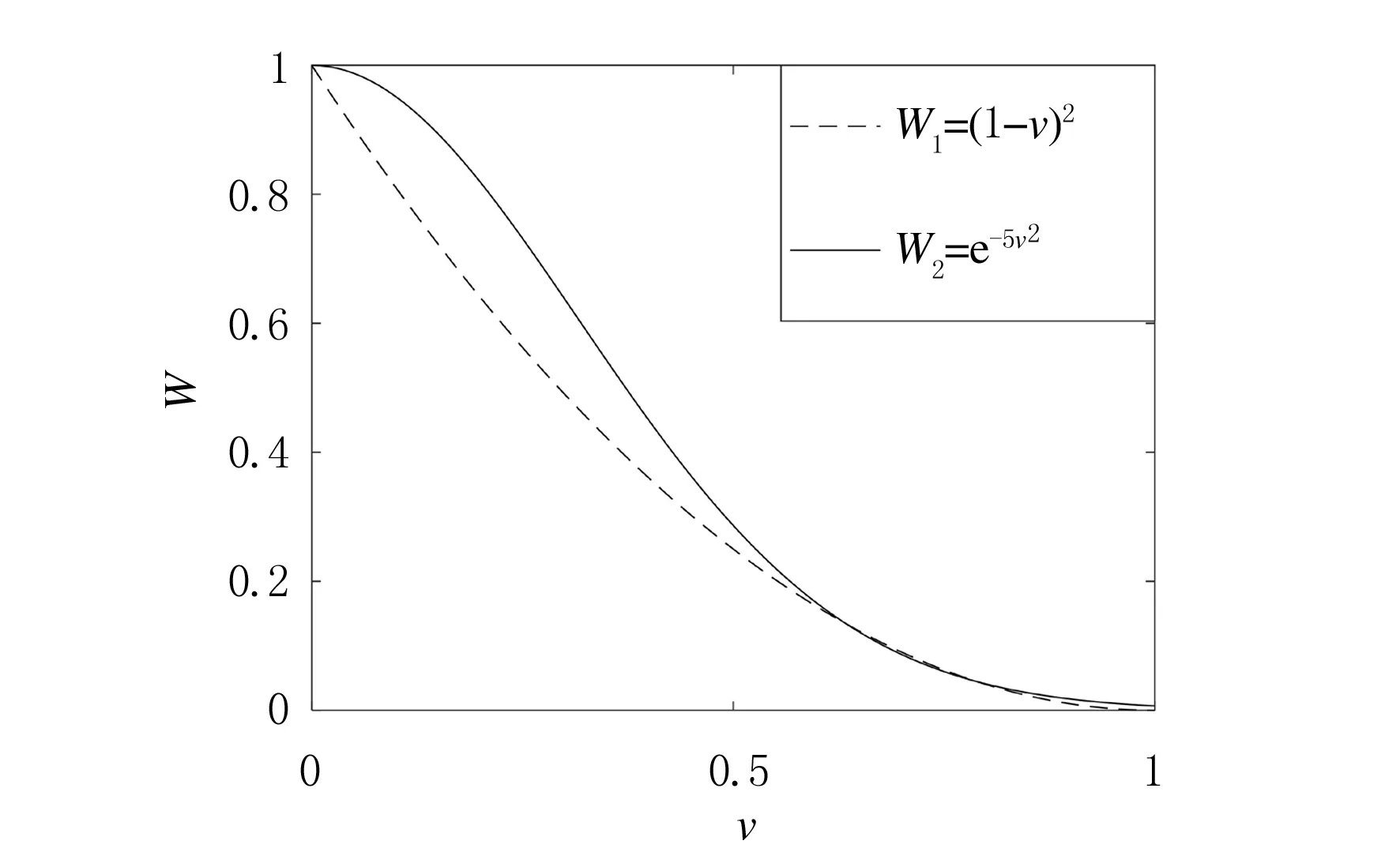
图1 W1(v)和W2(v)函数对比图

不同性质:W2(v)函数值降低,呈现先缓慢再加速的趋势.具体表现:在v→0+时,W2(v)函数值缓慢降低,保证了图像分割过程中边界清晰处能够较好、较完整地收敛,随着v的增大,W2(v)函数值加速降低,意味着平滑不清晰、较浅边界,即在近边缘处减缓衰减而在远边缘处加快衰减,从而提高对图像的弱边缘检测能力.

建立改进的Ambrosio-Tortorelli模型为

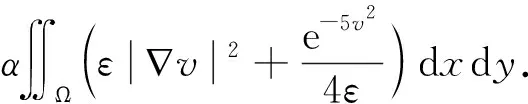
(4)

基于变分法计算式(4)对应的欧拉-拉格朗日方程:

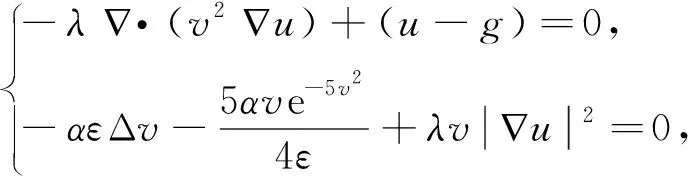
(5)

其中,边界处满足纽曼边界条件.

采用梯度下降法计算出式(5)对应的梯度下降流:

(6)

其中

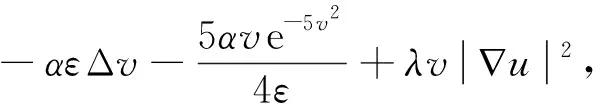
最后采用有限差分法离散式(6),得到改进Ambrosio-Tortorelli模型的迭代方程为

(7)

其中,

3 数值实验分析

3.1 图像分割介绍

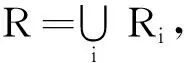
3.2 收敛性分析

本节实验在Window 10操作系统下,利用Matlab R 2017a软件编写程序实现.利用数值实验结果,分析改进Ambrosio-Tortorelli模型的收敛性.将原始图像(图2)进行分割实验,参数设置为α=0.4,λ=180,ε=0.7,迭代次数为1 000,得到图像分割后光滑图像u和边界图像v(如图3、图4).

图2 原始图像

图3 光滑图像u(迭代次数从1～1 000)

图4 边界图像v(迭代次数从1～1 000)

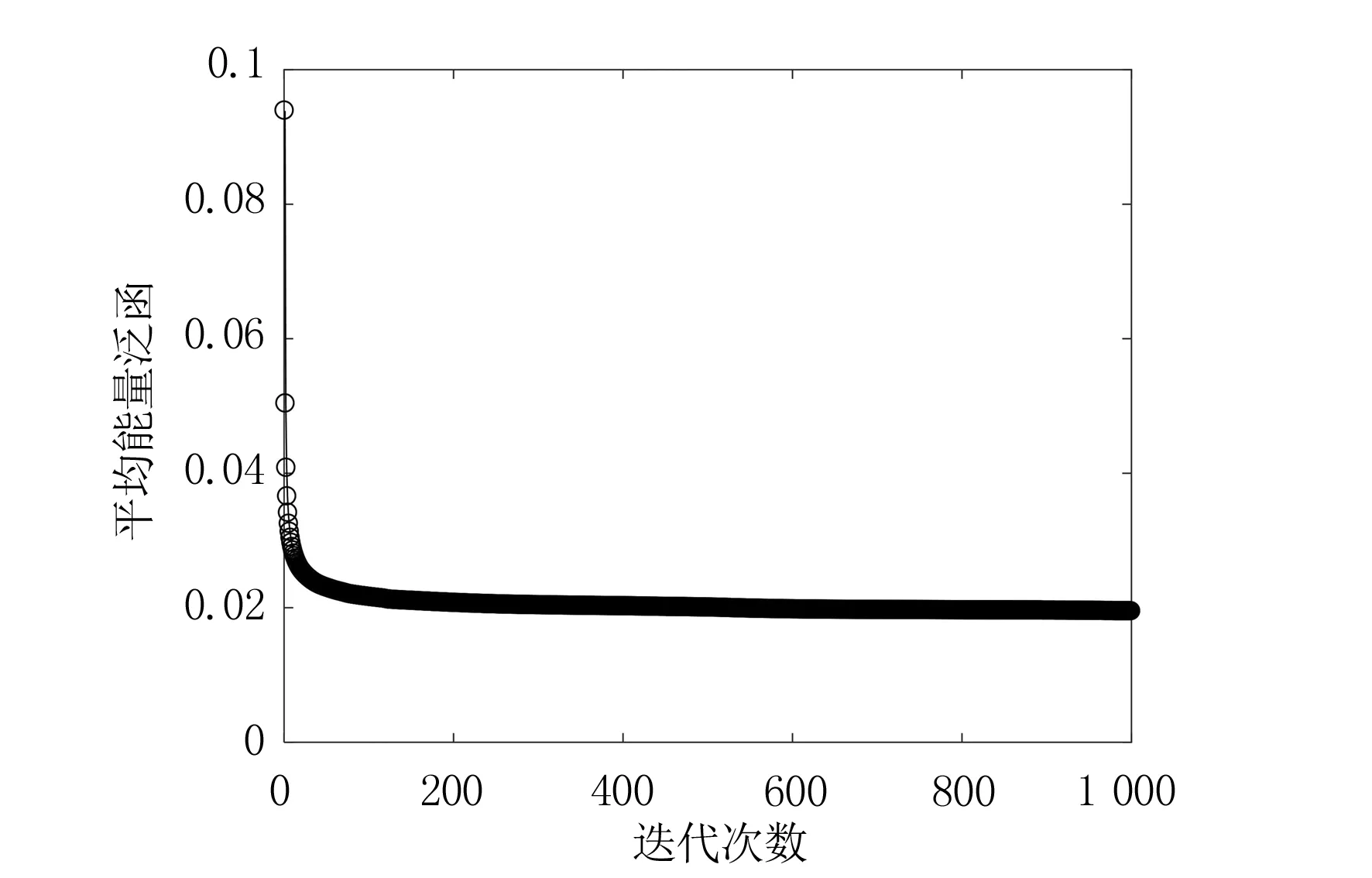
图5 平均能量泛函变化图

图6 Nu值变化图

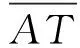
3.3 对比分析

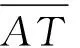
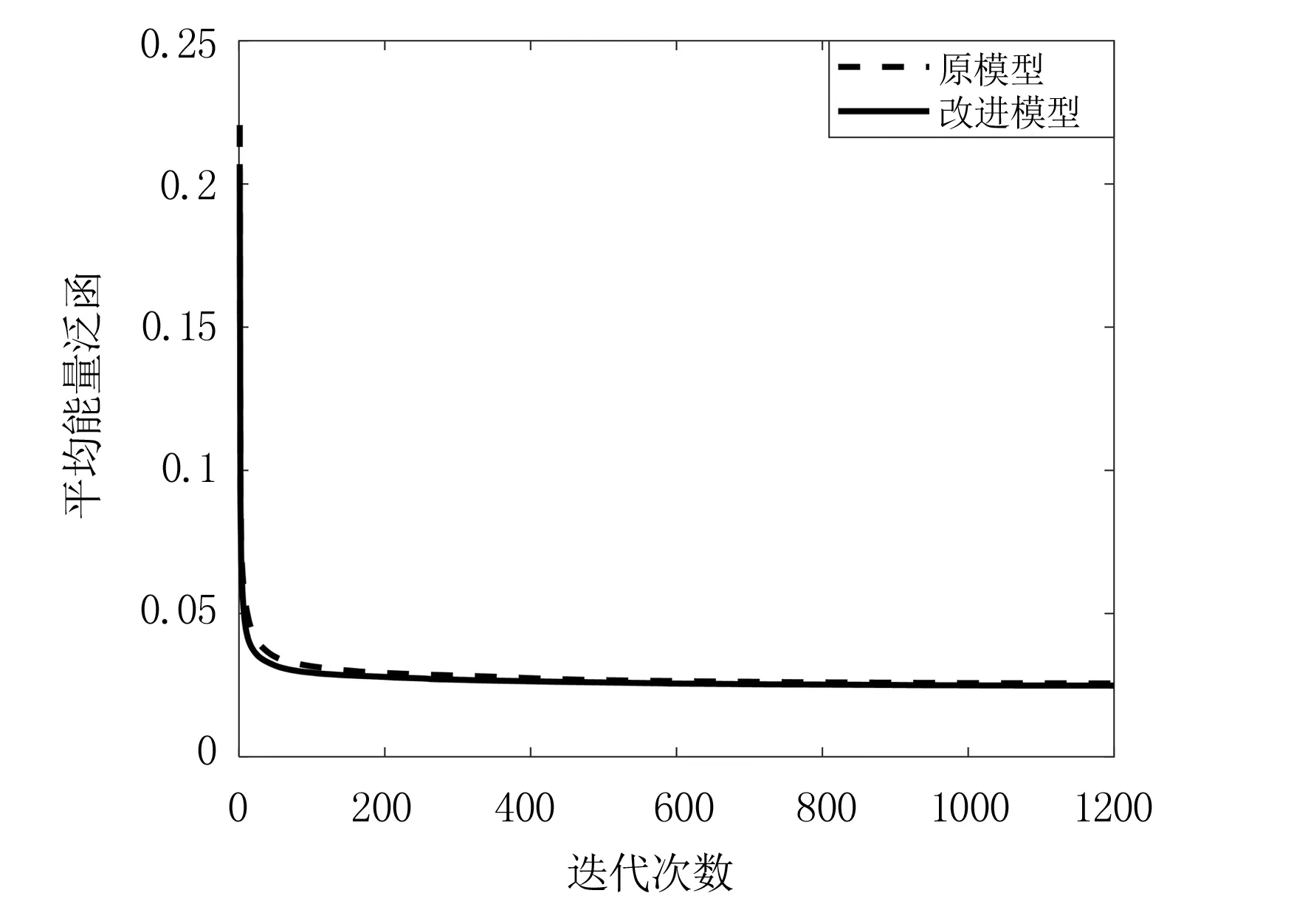
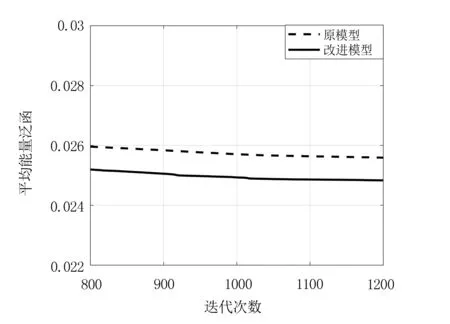
注:下图为上图放大呈现图9 平均能量泛函变化图

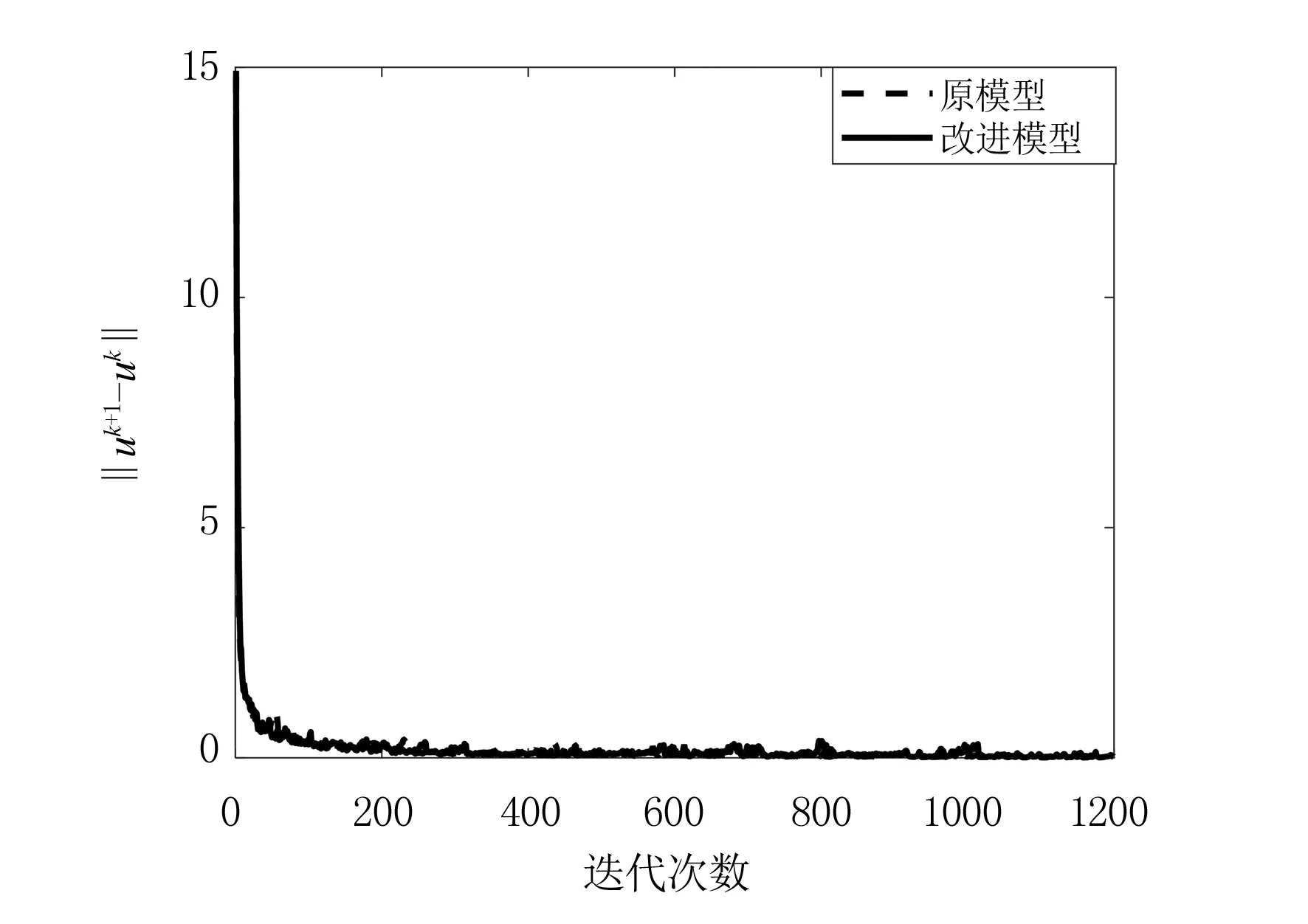
图10 Nu值变化图

4 结语

数值实验结果说明,改进Ambrosio-Tortorelli模型的图像分割应用具备有效性,且具有更恰当的衰减模式,能改善原模型中图像边缘测度逼近项随梯度模衰减过早且速度较慢等不足,在一定程度上提高了对图像弱边缘的辨识能力,即实现了图像弱边缘检测能力的提高.