我国股票市场波动性分析

□文/余康兴 李晓云

（南京大学 江苏·南京）

［提要］我国的股票市场是全球波动性较大的几个股票市场之一，对其进行波动性分析，对我国股市长期稳定健康发展具有重要的促进作用。本文选取2006年1月4日到2018年12月28日年上证指数日收盘价的数据，利用GARCH族模型综合性的对我国股票市场进行波动性分析，结果发现：我国股票市场在波动上具有非对称性和杠杆效应的特征，并且存在波动聚集现象。

引言

我国股票市场从成立至今已有30余年，一直在不断摸索着前行的道路，逐步走向完善。由于全球经济一体化的进程逐步加快，金融市场在整个经济运行中发挥着越来越重要的作用，一个国家如果拥有一个稳定健康发展的金融市场，对该国实体经济不断向前发展也会起着较大的促进作用。而股票市场作为金融市场的重要组成部分，对我国的资金融通和资金合理配置方面具有重要的影响。但是，如果对其监管不到位，股票市场的波动幅度一直较大，极易出现资源错配、信用危机等严重后果，进而严重影响实体经济的发展，因此对我国股票市场的波动性进行分析对维护金融市场稳定与保持实体经济健康发展具有一定的意义。

ARCH模型，是由Engle在1982年提出，该模型的主体思想是模型中的残差项的条件方差与其前期的值的大小相关。由于ARCH模型中需要进行大量的参数估计，但是要保证所有参数都满足约束条件是十分困难的，因此Bollerslev和Taylor在此基础上提出GARCH模型，由于GARCH模型只需包含3个参数即可表达，所以相比于ARCH模型中存在无穷多个参数的方程在参数估计上具有一定的优势。Zakoian和Olosten针对纽约股票市场中存在的非对称性问题提出TGARCH模型。Nelson通过对标准90指数的波动性进行研究，提出指数GARCH模型，该模型可以很好地解释股票波动性的杠杆效应。

本文选取2006年1月4日至2018年12月28日上证指数日收盘价的数据，并通过构建GARCH族模型，根据AIC准则选取最适宜研究股票市场价格波动性的模型，并结合模型所得出的结果对我国股票市场特征进行分析。

一、模型简介

（一）ARCH模型。ARCH模型是由Engle于1982年首先提出，该模型的原理如下：

在方差方程中的（p+1）个参数α0，α1，α2，…，αq和均值方程中的β0，β1，β2，…，βp都需要使用极大似然估计法进行估计。

由于ARCH模型中需要进行大量的参数估计，要保证所有参数都满足约束条件是十分困难的，并且ARCH模型在建立过程中假定正的冲击和负的冲击对该模型所产生影响是等同的，所以在研究波动率时是不存在杠杆效应的。因此，Engle的学生Bollerslev和Taylor为了解决老师所建立的模型中的不足之处，他们就此提出GARCH模型。

（二）GARCH模型。GARCH模型的原理如下：

从GARCH模型的方差方程可以看出，GARCH模型仅仅需要3个参数就可表达，而ARCH模型则存在无穷多个参数的方程，这无疑对模型的参数估计方面提供了一定的便利。并且使用GARCH模型可以起到降阶的作用，提高整个模型的精准度。后来，Zakoian和Olosten在对纽约股票市场波动性进行研究时发现该市场中存在着非对称性，而用现有的GARCH模型很难解释非对称性的存在，所以这两位学者在此模型的基础上提出了TGARCH模型用以解决该问题。

（三）TGARCH模型。该模型如下：

式中，dt-1为一个虚拟变量，且当ut-1＜0时，dt-1=1，否则dt-1=0。只要γ≠0，则说明存在非对称性。在该方程中非对称项为γ×u2t-1dt-1。观察该模型可见，好消息（ut-1＞0）和坏消息（ut-1＜0）对模型的影响是不一样的。由于当ut-1＜0时，dt-1=1，否则dt-1=0。对于好消息来说，ut-1＞0，dt-1=0，也就是说γ×u2t-1dt-1这项为0，因此好消息给模型带来的是α倍的冲击；而坏消息给模型带来的则是（α+γ）倍的冲击。因此，若γ＞0，则非对称效应会使得该市场的波动性逐渐加强；相反，如果γ＜0，则非对称效应会使得该市场的波动性逐渐减弱。

（四）EGARCH模型。由于上述三个模型不能很好地解释杠杆效应的存在，所以Nelson在1991年提出EGARCH模型，其表达式如下：

从该模型公式中可以看出，杠杆效应是指数型的，且当γ＜0时，杠杆效应是较为明显的，对于股票市场来说，它所受到的负向冲击导致其产生的波动要大于它所受到的正向冲击所引起的波动，具有杠杆效应。

二、基于GARCH族模型我国股票市场波动性实证分析

（一）数据来源。本文选取2006年1月4日到2018年12月28日年上证指数日收盘价的数据作为本次研究的指标，共计3，159条数据，数据来源于国泰安财经研究数据库，上证指数在后面的实证分析中用符号zs来表示。

（二）上证指数波动的基本分析。从表1可以看出，在所选取的期间内，我国上证指数的中位数与最大值和最小值之间相差的较大，说明我国上证指数波动性较大。上证指数的偏度系数为1.029514＞1，说明上证指数是有偏的，且是向右偏的。峰度系数为4.843304＞3，且JB统计量的p值小于0.05，则说明我国股票价格不服从正态分布，且其分布具有厚尾性。（表1）

表1 我国上证指数基本统计量一览表

上证综合指数QQ散点图如图1所示。从图1可以看出，该序列在下端向下倾斜，而上端则向上翘起，表明上证指数的分布呈现出尖峰态的，且其尾部相对于正态分布来说更厚，且右尾高于左尾，这说明我国上证综合指数的波动呈现出尖峰厚尾性。（图1）

图1 上证指数价格QQ散点图

三、模型的建立

由于是处理时间序列数据，以此需对该序列进行平稳性检验，根据ADF检验结果发现，ADF统计量的值为-25.22083，小于在5%统计量的临界值，因此拒绝原假设，由此可看出该序列是平稳序列。由于股票价格指数序列经常使用一种带漂移项的随机游走模型来描述，因此该模型的基本方程如下：zs=μ+ρ×zs（－1）＋ut，根据表2的回归结果，可以得出模型的表达式如下：zst=8.336115+0.997198×zst-1＋ut，根据最小二乘法的回归方程可以得到该模型的残差序列，如图2所示。根据图2可以看出，波动出现了成群的现象，波动在一段时间较小，而在另一段时间则较大，说明该模型可能存在条件异方差性。因此，需对该模型进行ARCH-LM检验，当滞后阶数p=5时，检验结果见表3，据检验结果所示，在5%的显著性水平下拒绝原假设，表明该模型中存在ARCH效应，由于滞后阶数为5阶时，LM统计量的相伴概率仍为0，说明该模型可能存在高阶ARCH效应。（表2、图2、表3）

表2 最小二乘法回归结果一览表

表3 ARCH-LM检验结果一览表

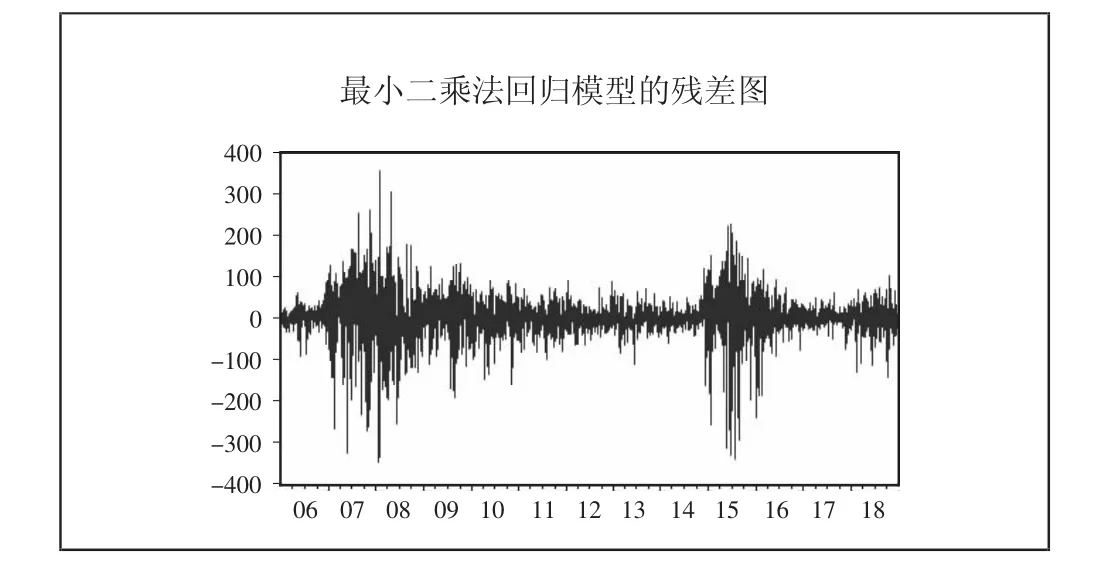
图2 最小二乘法回归模型的残差图

（一）GARCH模型。由于存在高阶ARCH效应，而低阶GARCH模型能很好的解释高阶的ARCH效应，所以使用GARCH（1，1）模型对模型进行拟合，拟合结果如表4所示。（表4）

表4 GARCH模型回归结果一览表

根据表4的结果，可以得到回归模型的表达式：

接下来，对所构建的模型进行ARCH-LM检验，结果显示P值大于0.05，说明使用GARCH模型消除了条件异方差。根据GARCH模型的回归结果，ARCH和GARCH项的系数之和为0.999801，接近于1，这说明了外部冲击会对我国股票市场的波动产生一定的影响，并且所受到的冲击是持久的。由于GARCH模型不能解释我国股票市场存在的非对称性和杠杆性，所以需要对该模型进行改进。

（二）TGARCH模型。因为低阶的TGARCH模型在解释高阶ARCH效应时效果较好，所以选择最大阶数为2的4种TGARCH模型，根据赤池信息量原则选取最优模型，结果见表5。由表5可以看出，TGARCH（1，1）模型的AIC值比其他三个模型的AIC值要小，说明选择TGARCH（1，1）模型能够更好地反映我国股票市场的波动情况。（表5）

表5 TGARCH模型AIC检验结果一览表

因此，在这里构建TGARCH（1，1），结果见表6。（表6）

根据回归结果，可以得到TGARCH（1，1）模型的表达式为：

由于γ=-0.037874≠0，说明我国股票价格的波动呈现出非对称，而好消息会给股市带来0.075518倍的冲击，坏消息会给股市带来0.075518-0.037874=0.037644倍的冲击要小于好消息的冲击，而γ＜0，这说明我国股票市场中存在的非对称效应会使得股市的波动逐渐减弱。由于TGARCH模型在解释股票市场中的杠杆效应时略显不足，所以需要引进EGARCH模型对上证指数波动的杠杆性进行分析。

（三）EGARCH模型。类似于TGARCH模型，首先通过AIC准则来选择最优模型，EGARCH模型的AIC结果如表7所示。通过表7可以看出，EGARCH（1，1）模型的AIC值最小，可见EGARCH（1，1）为最优模型。因此，在这里构建EGARCH（1，1）模型，结果见表8。（表7、表8）

表7 EGARCH模型AIC检验结果一览表

表8 EGARCH（1,1）模型估计结果一览表

EGARCH（1，1）模型的表达式为：

通过比较EGARCH（1，1）模型与前面所构建的TGARCH（1，1）和GARCH（1，1）模型的AIC值可以发现，EGARCH（1，1）的AIC值是最小的，说明该模型拟合数据的效果较好。通过EGARCH（1，1）模型的结果可以清楚地发现非对称项系数γ=0.027628≠0，说明非对称性的现象存在。当ut-1＞0时，外在冲击对条件方差存在一个0.123622+0.027628=0.15125倍的冲击，而当时ut-1＜0，外在冲击对条件方差存在一个0.123622-0.027628=0.095994倍的冲击，由此可以明显看出我国股票市场上存在着杠杆效应和非对称效应。

四、结论

本文首先对2006年1月4日到2018年12月28日上证指数日收盘价的数据对上证指数进行统计描述分析、平稳性分析和ARCH效应检验，发现我国上证综合指数在波动上呈现出尖峰厚尾性，并且该序列经ADF检验后平稳，但在进行ARCH-LM检验时发现该模型存在高阶ARCH效应，因此我们通过构建GARCH族模型来解决该问题，并根据AIC原则构建了GARCH（1，1）、TGARCH（1，1）、EGARCH（1，1）这3个模型，由于EGARCH（1，1）模型的AIC值最小，并且相比与其他两个模型，该模型能更好地解释我国股票市场中是否存在非对称性和杠杆效应，因此选择EGARCH（1，1）模型作为最优模型以分析我国股票市场的波动情况。根据该模型的结果可以发现，非对称项系数不为0，说明我国股票价格波动中存在着非对称性，而通过观察模型的结果可以发现好消息对股市所造成的冲击要大于坏消息的冲击，并且根据该模型的残差序列图可以发现，我国股票价格的波动具有波动聚集的现象。