基于不变扩展卡尔曼滤波的无人机姿态估计

李世强, 易文俊

(南京理工大学 瞬态物理国家重点实验室,江苏 南京 210094)

近年来,无人机迎来了大发展,被广泛用于军事侦察、安防巡检、灾后搜救、农业生产以及摄影航拍等不同领域,其中尤以四旋翼飞行器(以下简称“四旋翼”)最为流行。许多研究人员也对四旋翼产生了浓厚的兴趣,搭建了多种飞行平台,实验了不同的控制算法。飞行器要实现稳定可靠飞行,必须准确高效地获取自身的各种状态信息。而四旋翼本质上是一个欠驱动系统,只能产生垂直于机体平面的升力,姿态估计信息被用于最底层控制环路以稳定飞行器,因此快速准确的姿态估计算法尤为重要,飞行控制算法的稳定性和可靠性直接依赖于姿态解算的精度和速度[1]。

由于受到成本、载荷和尺寸的限制,四旋翼普遍依赖惯性测量单元 (Inertial Measurement Unit,IMU)估算姿态。IMU是一组传感器,由测量加速度的加速度计和测量角速度的陀螺仪组成,通常还包括一个磁力计来测量地球的磁场。这3个传感器中的每一个都产生一个3轴测量值,总共构成一个9轴测量值。但IMU不提供直接的姿态估计,为了提高性能和鲁棒性,必须对原始信号进行非线性滤波和数据融合处理,方能重建平滑的姿态估计和校正角速度测量的偏差。此外,从不同的传感器测量结果中同时估计姿态和陀螺仪偏差大为有益[2]。

刚体姿态估计问题极具挑战性,几十年来一直是导航研究的焦点。这是因为刚体旋转的基本位形空间,即特殊正交群SO(3)不是向量空间而是弯曲空间,所以姿态估计本质上是非线性问题[3]。简单直接地用局部坐标(例如欧拉角、Rodrigues参数)来表示旋转存在诸多问题。局部坐标包含需要进行特殊处理的奇异点(例如当俯仰角为90°时),并且估计既取决于局部坐标的选择,也取决于固定和移动参考坐标系。如果将标准向量空间中的滤波方法不加改造地用到姿态的局部坐标表示上,则不仅状态空间动力学方程和测量方程高度非线性,依赖于参考坐标的选择,而且滤波性能在位形空间的不同区域高度不均匀[4]。

许多滤波方法都致力于处理非最小姿态表示所固有的约束。乘性扩展卡尔曼滤波器(Multiplicative Extended Kalman Filter,MEKF)因其灵活性和计算效率高而得到广泛应用。它利用旋转矩阵(或四元数)的几何结构,对在原点处线性化的本征状态误差建立了误差状态卡尔曼滤波器。然而,当动态、测量模型高度非线性或没有良好的先验状态估计时,MEKF容易出现发散现象[5]。

不变观测器理论基于估计误差在矩阵李群的作用下不变[6],该性质被称为系统的对称性[7],推动了不变扩展卡尔曼滤波(Invariant Entended Kalman Filter,InEKF)的发展[8-9],在即时定位与地图构建(Simultaneous Localization and Mapping,SLAM)[10]和辅助惯性导航系统[11]中得到成功应用并取得良好效果。由InEKF算法可知,如果状态定义在一个李群上,并且动力学方程满足“群仿射”特性,那么对称性使得估计误差满足李代数上的“对数线性”自治微分方程[8]。在确定性情况下,该线性系统可以用来精确地复原在群上演化的非线性系统的状态估计。因此,对数线性特性允许设计一个非线性观测器或具有强收敛特性的状态估计器[12]。

在本文中,基于InEKF理论解决李群SO(3)上的姿态估计问题,建立连续时间运动模型和离散时间观测模型。定义的确定性系统满足“群仿射”特性,因此,误差动态是对数线性的。在实践中,随着传感器噪声和IMU偏差的引入,该对数线性误差系统只是近似成立,在许多情况下,由于优越的收敛性和一致性,InEKF仍然表现良好。可以通过MATLAB仿真实验来证明所开发滤波方法的效用和准确性。

1 理论背景及预备知识

首先回顾一些有关特殊正交群SO(3)及其李代数so(3)的基本知识和有用的数学公式,这将在后面的章节中用于推导InEKF算法。

SO(3)中的元素由满足RTR=I,det(R)=1的3×3实矩阵R组成,这里的I表示3×3单位矩阵。SO(3)是一个矩阵李群,与其相关联的李代数记为so(3),是3×3斜对称矩阵。为方便计算,令(·)∧表示R3到so(3)的线性映射。

(1)

so(3)和SO(3)之间由指数映射exp建立联系:

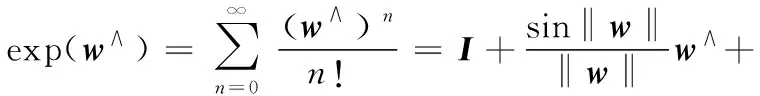
(2)

式中:‖·‖为标准向量范数。为方便,记Exp(w)=exp(w∧)。

对于任意R∈SO(3),w∧∈so(3),有伴随映射Rw∧RT=(Rw)∧。另外,定义J为SO(3)的左雅可比,有

(3)

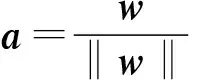
在SO(3)中运动的连续轨迹R(t)有

(4)

(5)

对fw(R)有

fw(R1R2)=R1R2w∧

=fw(R1)R2+R1fw(R2)-R1fw(I)R2

(6)

式(6)即为“群仿射”特性[8]。由于“群仿射”特性,右和左不变误差是轨迹独立的,即满足

=0

(7)

=ηlw∧-w∧ηl

(8)

(9)

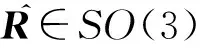
2 建立模型

在描述InEKF算法之前,首先需要建立坐标系,定义符号系统,建立四旋翼无人机姿态运动模型,描述传感器测量模型及其基本假设。

2.1 参考坐标系

为了描述四旋翼无人机的姿态,以及讨论加速度计和陀螺仪的测量值,必须引入一些参考坐标系。通常定义两个坐标系表达姿态角的关系,一般使用导航坐标系(N系)和机体坐标系(B系)。导航坐标系,即当地的地理坐标系,相对大地水平面定义,坐标轴Xn,Yn,Zn分别指向地理上的北、东和当地垂线方向(向下),即北东地(NED)坐标系。机体坐标系则使用标准右前上坐标系,坐标轴Xb,Yb,Zb分别指向无人机的右侧、前方以及上方。机体坐标系到导航坐标系的坐标变换矩阵用R表示,即无人机的姿态。

2.2 运动模型和测量模型

四旋翼无人机由旋转矩阵表示的连续时间姿态运动方程为

(10)

式中:Ω∈R3为无人机在机体系内的瞬时角速度,由陀螺仪测量。然而测量结果被加性高斯白噪声过程干扰,即

(11)

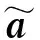
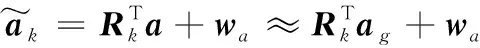
(12)

(13)

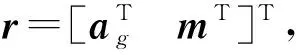
(14)

式中:Vk∈R6是由wa和wm组成的高斯噪声。则有

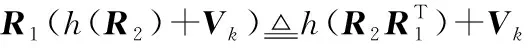
(15)

3 不变扩展卡尔曼滤波

3.1 预测

考虑完整的系统运动方程和测量方程:

(16)

噪声wΩ的引入,使得右不变误差η变为

(17)

(18)

(19)

(20)

3.2 测量更新

为了将新的测量值纳入考量,记zk∈R6为更新量,取为

(21)

状态校正方程为

(22)

η+=Exp(Kkzk)η

(23)

式中:Kk为时刻tk的卡尔曼增益矩阵,同样用η=Exp(ξ)≈I+ξ∧进行一阶近似将式(23)线性化,忽略高阶项,有

η+≈I+ξ+∧≈I+ξ∧+(Kkzk)∧

(24)

因此

ξ+=ξ+Kk((I-ξ∧)r-r+Vk)

=ξ+Kk(-ξ∧r+Vk)

=ξ+Kk(Hξ+Vk)

(25)

最后,可以利用导出的线性更新方程和卡尔曼滤波理论将InEKF的状态和协方差更新方程写成

(26)

式中:卡尔曼增益矩阵Kk由式(27)计算

(27)

由式(25)可得灵敏度矩阵H和测量噪声协方差N为

(28)

3.3 引入陀螺仪偏差

在硬件上实现基于IMU的状态估计算法通常需要对额外的状态加以考虑,如陀螺仪和加速度计的偏差。可以使用两种不同的方式来进行处理。一种是将偏差作为一个恒定的参数,假设它通常在比实验时间更长的时间段内变化,然后可以在一个单独的实验中对偏差进行预校准。另一种是视偏差为所估计的状态的一部分,则可以在估计姿态时同步估计偏差。本文采用后一种方式,因为在线实时补偿偏差的影响能提高姿态估计的精度。但是,一旦将偏差纳入考虑,则没有李群可以满足动力学方程的群仿射特性。尽管InEKF的许多理论性质不再成立,但仍能设计一个“增广InEKF”,其性能仍然优于标准EKF[14]。由于两种偏差的处理过程相似,为节省篇幅,本文只考虑陀螺仪偏差。

陀螺仪的偏差b是缓慢时变信号,以加性的方式破坏测量结果

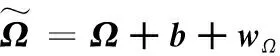
(29)

模型的状态现在变为坐标变换矩阵R和偏差b,χ=(R,b)∈SO(3)×R3。现在定义增广的右不变量误差为

(30)

式中:ζ为偏差误差。

(31)

偏差b动态使用典型的“布朗运动”模型建模,即导数是高斯白噪声,以捕捉参数缓慢时变性质:

(32)

为了计算线性化的误差动态,首先对增强的右不变误差进行微分。在执行链式规则并进行一阶近似后得

(33)

误差动态只通过噪声wΩ和偏差误差ζ依赖于估计轨迹。当没有噪声wΩ和偏差误差ζ时,误差动态对估计轨迹没有依赖。现在可以从中构建一个线性系统,得到

(34)

测量方程不依赖于IMU的偏差。因此,对增强的右不变误差,H矩阵可以简单地附加零以满足维度要求。线性更新方程成为

(35)

最终,包括陀螺仪偏差b的“增广InEKF”方程,可以完整写出。估计状态使用以下一组微分方程进行预测传播。

(36)

增广的右不变误差动态的协方差通过解Riccati方程计算

(37)

式中:矩阵A,B由式(34)给出。估计状态更新方程为

(38)

(39)

3.4 离散化

在前面的章节中,滤波状态传播方程是连续时间的。然而,为了实现滤波过程,这些方程需要离散化。为此,对惯性测量量(即输入)做零阶保持,并进行积分。偏差动态是简单的高斯噪声,因此,离散形式确定性动态方程为

(40)

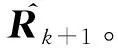
(41)

式中:Δt=tk+1-tk。为了更新协方差,需要解一个连续时间的Riccati方程(37),它的解析解为[13]

Pk+1=Φ(tk+1,tk)PkΦ(tk+1,tk)T+Qd

(42)

其中,离散噪声协方差矩阵为

(43)

状态转移矩阵Φ(tk+1,tk)满足:

(44)

求解式(44)得到[12]:

(45)

与状态转移矩阵类似,离散噪声协方差矩阵也有一个解析解。不过实践中,这个矩阵通常被近似为Qd≈ΦQΦTΔt。

4 数值模拟

使用 MATLAB 对前述不变扩展卡尔曼滤波算法进行仿真实验,证明了所提出的不变扩展卡尔曼滤波方案的有效性。为了进行较为真实的仿真,首先从一个实际的陀螺仪上采集一组真实的角速率测量值。采样速率为60 Hz。从R0=I开始,真实姿态矩阵由下式迭代生成:

Rk+1=Rk(ΩΔt)

初始陀螺仪偏差的真值设置为b0=[-0.1 0.1 0.1]Trad/s。然后生成一组数据为

(46)

陀螺仪噪声wΩ有0.001 rad/s的标准差,陀螺仪偏差b的过程噪声方差为Σb=0.0012Irad2/s4,而磁力计和加速度计噪声Σa=Σm=0.01I。

将所提方案与经典的MEKF相比较,MEKF同样采用旋转矩阵作为姿态表示。进行50次Monte Carlo实验,得到两种方案的姿态估计误差的变化如图1所示。

图1 姿态估计误差的变化图

从图1中可以看出,由于两种方案都采用旋转矩阵表示,在滤波预测阶段过程方程也相同,从而姿态估计误差相差极小。由于姿态误差呈周期性波动,故采用最后15 s的误差平均值进行比较。50次仿真结果的均值与标准差如表1所示。

表1 50次仿真最后15 s姿态估计误差

可以看出在姿态估计误差方面InEKF比MEKF略有优势。而对陀螺仪偏差的估计如图2所示。

图2 陀螺仪偏差估计误差的变化图

由图2可以看出在姿态估计误差相对稳定之后,InEKF估计的陀螺仪偏差要更加接近真值。图3是滤波过程结束时刻陀螺仪偏差误差的箱线图。

图3 滤波过程结束时刻陀螺仪偏差误差的箱线图

由图3可以看出InEKF估计的陀螺仪偏差整体更优,InEKF误差的平均值为0.008 947,而MEKF的平均值为0.010 850,InEKF比MEKF的精度提高了约18%,具体数据如表2所示。某次滤波过程开始阶段和中间一段时间陀螺仪偏差的变化如图4和图5所示。

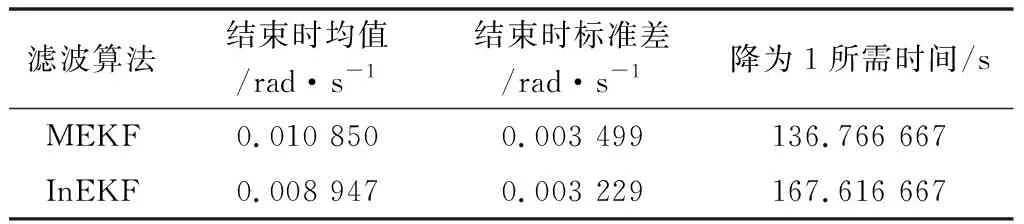
表2 仿真中陀螺仪偏差误差统计量

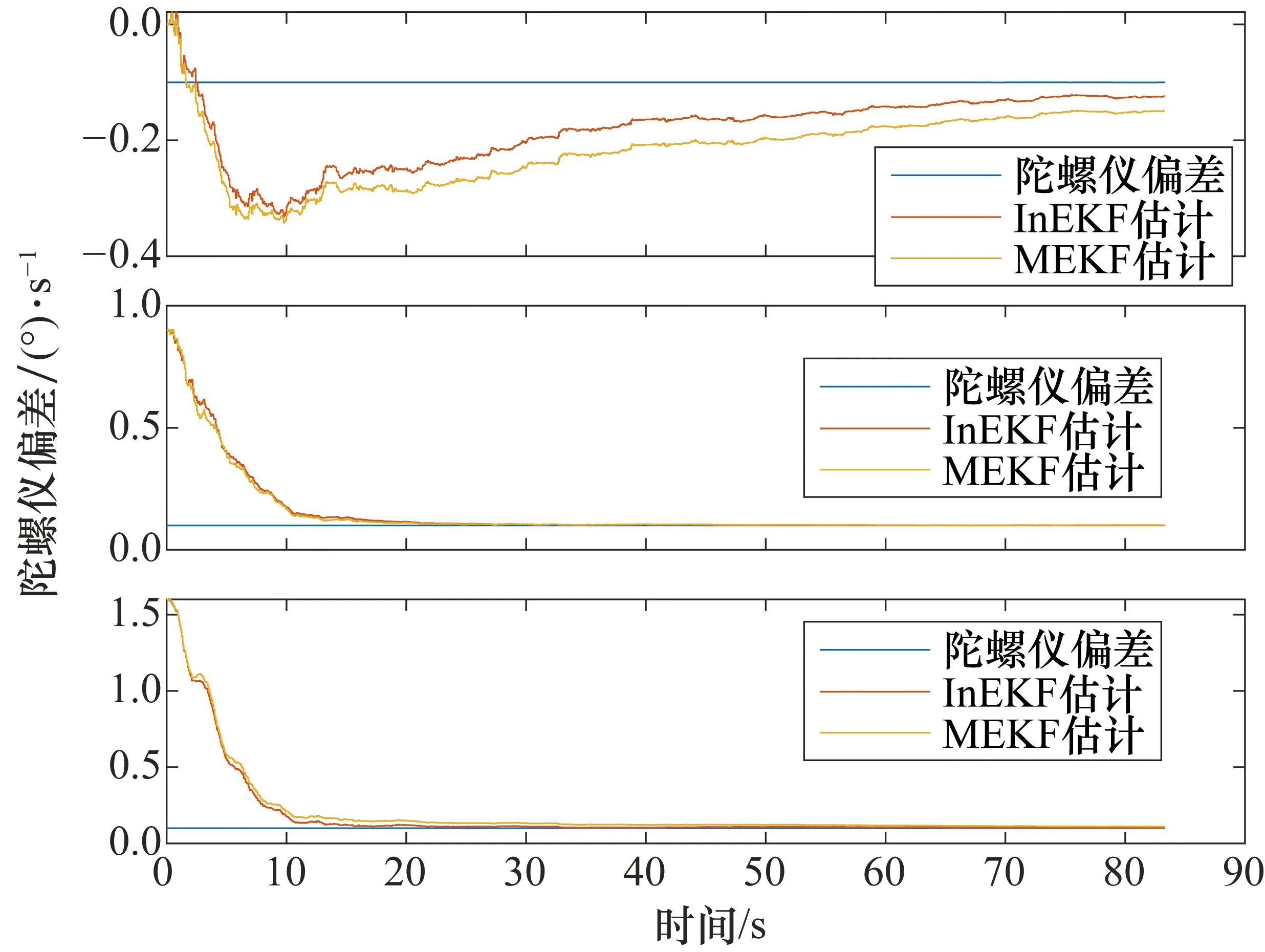
图4 某次仿真开始阶段陀螺仪偏差的变化图

图5 某次仿真中间阶段陀螺仪偏差的变化图

从变化轨迹可以看出,InEKF的估计比MEKF收敛到真值附近的时间更快,证明了该方法具有优越性。

5 结束语

本文提出了一种InEKF算法,用于同时估计无人机姿态和陀螺仪偏差。借助特殊正交群SO(3)的李群特性,推导出一种在SO(3)×R3中运动的连续时间随机非线性滤波算法,该算法的主要特点是将姿态估计结果和估计误差表示为SO(3)的元素,通过指数映射推导误差动态的近似一阶线性微分方程,从而减小误差动态对当前估计值的依赖,增强了滤波算法对初值不确定的鲁棒性。通过仿真将该算法与经典的MEKF算法进行比较,仿真结果表明所提出的滤波算法在保持姿态估计精度的同时,能提供更优的陀螺仪偏差估计,验证了该算法在精度和滤波收敛性等方面具有优越性。