用“分与合”的结构图理解加减法关系

文 |张欣怡

如何借助半抽象的“分与合结构图”帮助学生进一步理解加减法的部总关系呢？

一、提取部与总，理解结构图

1.呈现问题：你能根据三个算式，分别填一填结构图吗？（如图1）

图1

2.反馈后比较：为什么算式不同，结构图却相同？

3.交流发现：三个算式虽然不同，但结构图相同，本质都是4、9、13三个数之间的关系：13是总数，可以分成4和9两个部分数。

4.呈现逆向练习组。

（1）请根据图写出算式（如图2）

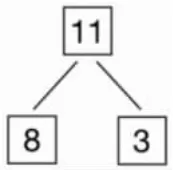
图2

（2）编一组数据，填图写算式（如图3）

图3

二、拆解部与总，解释结构图

1.呈现问题：点子图对应的结构图是哪一幅？连一连，再根据结构图写出算式（如图4）。

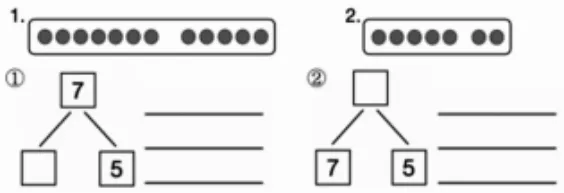
图4

2.反馈后讨论：两个结构图都有7和5，为什么对应的点子图不一样？

3.交流发现：两个结构图中的7、5意义不同，结构图①中7是总数，5和2是部分数，结构图②中7和5是部分数，12是总数。

三、转化结构图，建立基本模型

1.出示题目（如图5、6），补全算式和结构图。

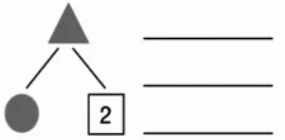
图5

2.反馈交流：图5你是怎么写出“●+2=▲”的？图6你是怎么找到●和★的位置，又是怎么写出两道减法算式的？

图6

3.总结：只要分清总量和部分量，就能把结构图和算式补充完整了。

四、应用结构图，解释基本模型

1.出示任务：根据题目中的数量关系，把结构图补充完整（如图7、8、9）。

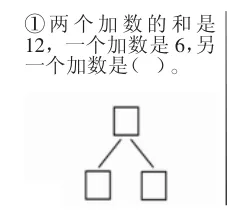
图7

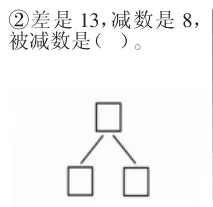
图8

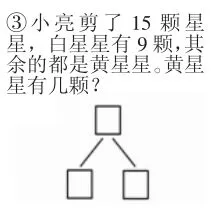
图9

2.全班交流，分析加减法关系。

3.呈现结构图（如图10），请学生模仿上一环节的三道文字题编题。

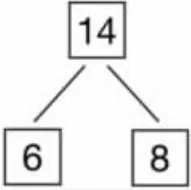
图10

“分与合”的结构图实质上就是一个整体与部分的实物原型，在理解加减法实质中起到了极其重要的作用。本节课通过结构图与加减法算式、符号代数式、问题情境等不断关联与转换，直观引导学生理解加减法的本质：“一个整体（类）与两个部分（类）的相等关系”。