2022年高考海南卷物理第8题评析及变式探讨

赵继辰

(北京教育学院数学与科学教育学院 北京 100044)

我国的石拱桥具有悠久的历史,体现了古代劳动人民的智慧.新版普通高中物理课程标准在学科核心素养模块中提出了科学态度与责任,在认识科学、技术、社会、环境关系的基础上,逐渐形成探索自然的内在动力、严谨认真和持之以恒的科学态度,以及保护环境的责任感[1].而对石拱桥模型的静力学原理分析,正可诠释科学本质、科学态度、社会责任等要素.

1 试题分析

【题目】(2022年高考海南卷物理第8题)我国的石桥世界闻名,如图1所示,某桥由六块形状完全相同的石块组成,其中石块1、6固定,2、5质量相同为m,3、4质量相同为m′,不计石块间的摩擦,则m∶m′为( )

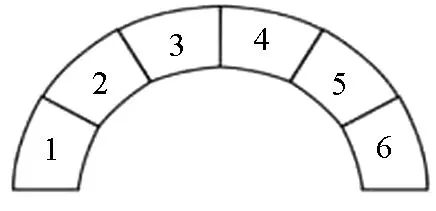
图1 石拱桥示意图

解析：根据图2所示石块3的受力分析可知

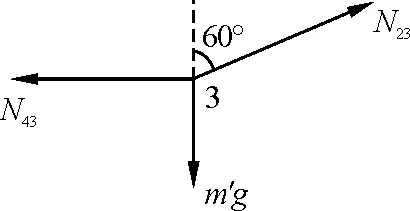
图2 石块3的受力分析图

N23cos 60°=m′g

根据图3所示石块2的受力分析可知

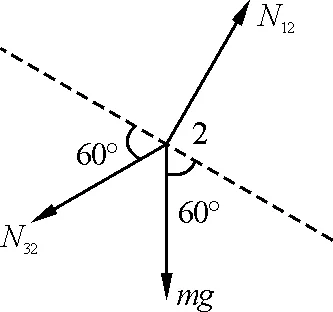
图3 石块2的受力分析图

N32cos 60°=mgcos 60°

因此m∶m′=2,故选项D正确.

2 变式探讨

变式1：如图4所示,某桥由2N块形状完全相同的石块组成,其中石块2N-1、2N固定,石块1、2的质量均为m,石块2n-1、2n(n=2,…,N)质量相同,不计石块间的摩擦,求石块2n-1的质量.

图4 2N块石块组成的石拱桥

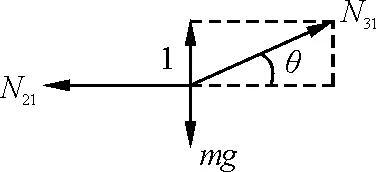
图5 石块1的受力分析图

根据石块1的受力分析(图5)可知

N31sinθ=mg

根据石块3的受力分析(图6)可知

图6 石块3的受力分析图

N13cosθ=N53cos 2θ

解得

根据石块5的受力分析(图7)可知

图7 石块5的受力分析图

N35cos 2θ=N75cos 3θ

解得

对比石块5和石块3的受力分析情况,我们发现

N75cos 3θ=N35cos 2θ=N13cosθ

由此可以推断出石块2n-1的受力情况

N(2n+1)(2n-1)cosnθ=N13cosθ

N(2n-3)(2n-1)sinθ=

解得

3 关联题型

如图8所示,石拱桥有9块完全相同的对称楔形石块组成,每块质量都为m,重力加速度为g,若接触面间的摩擦力忽略不计,则石块4对石块3的压力的大小为( )

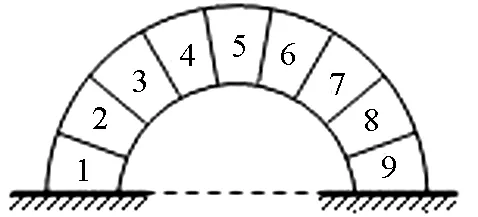
图8 9块石块组成的石拱桥

解析：在共点力平衡题型中,当题目中有多个研究对象且所要求解的问题并不涉及所有物体时要考虑使用整体法来求解.本题中要求解石块4对石块3的压力大小,那么就可以将石块4、5、6看成一个大石块,石块1、2、3以及石块7、8、9也分别看成一个大石块,这样就将9块质量都为m的小石块变为3块质量都为3m的大石块进行分析.受力分析如图9所示.

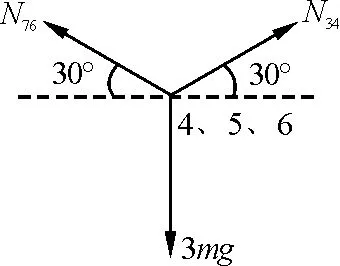
图9 石块4、5、6的整体受力分析图

根据大石块4、5、6的受力分析(图9)可知

2N34sin30°=3mg

本题构思巧妙,但存在科学性错误.石拱桥模型在摩擦力忽略不计的情况下,各石块的质量不会全部相同,否则无法保持平衡[2].我们不妨采用隔离法对石块5和4分别进行受力分析.

根据石块5的受力分析(图10)可知

图10 石块5的受力分析图

2N45sin 10°=mg

根据石块4的受力分析(图11)可知,在垂直于石块3、4之间压力N34的方向上,N54sin 20°>mgsin 60°,因此石块4无法保持平衡.

图11 石块4的受力分析图

要想使各石块保持平衡,那么它们的质量须遵从一定的关系,我们通过下道例题进行具体分析.

变式2：如图12所示,某桥由2N+1块形状完全相同的石块组成,其中石块2N+1、2N固定,石块2n+1、2n(n=1,2,…,N)质量相同,石块1的质量为m,不计石块间的摩擦,求石块2n+1的质量.

图12 由2N+1块石块组成的石桥

图13 石块1的受力分析图

根据石块1的受力分析(图13)可知

2N31sinθ=mg

根据石块3的受力分析(图14)可知

图14 石块3的受力分析图

N13cosθ=N53cos 3θ

解得

根据石块5的受力分析(图15)可知

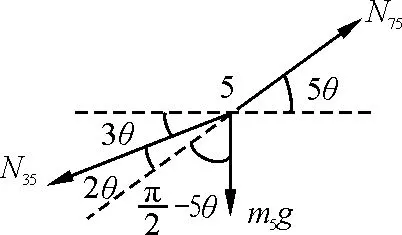
图15 石块5的受力分析图

N35cos 3θ=N75cos 5θ

解得

对比石块5和石块3的受力分析情况发现

N75cos 5θ=N35cos 3θ=N13cosθ

由此可以推断出石块2n+1的受力情况

N(2n+3)(2n+1)cos (2nθ+θ)=N13cosθ

N(2n-1)(2n+1)sin2θ=

m(2n+1)gcos (2nθ+θ)

解得

4 教学启示

共点力平衡是高考物理力学题中的典型问题,这其中三力平衡在考题中最为常见[3].解决此类问题一般分为三步:第一步对研究对象进行受力分析,明确已知力和要求解的力;第二步根据几何关系确定各力之间的夹角;第三步将已知力和要求解的力在垂直于无关力的方向进行分解,然后列写平衡方程进行求解.如遇多个研究对象,可采用整体法进行求解.