基于Savitzky-Golay平滑-小波降噪处理的桥梁结构监测数据分析方法

董 是,龙志友,毕洁夫,王建伟,邵永军,杨 超,左 琛,张士远,万昭龙

(1.长安大学运输工程学院,陕西 西安 710064; 2.道路基础设施数字化教育部工程研究中心,陕西 西安 710064;3.长安大学公路学院,陕西 西安 710064; 4.陕西高速公路工程试验检测有限公司,陕西 西安 710086)

近年来,随着我国公路网的纵横发展,在山区、河谷及高原等地的高速公路频繁使用连续刚构桥。连续刚构桥因其具有连续梁无伸缩缝、车辆通行平畅、保持不设支座、无需转换体系等优点,在大跨径桥梁工程中得到广泛使用[1]。但长期服役产生了结构劣势、抗力退化等问题,如跨中应力较大、构件变形或裂缝增大,主桥结构损伤。结构损伤会造成行车不便,情况严重时造成桥梁设施重大维修甚至报废处理,因此有必要在其服役期间进行结构健康监测[2]。

桥梁结构健康监测是利用现场的、无损的、实时的方式采集结构与环境响应信号,通过提取分析结构响应的特征,获取环境信息、分析结构内部力学响应[3],进而识别结构损伤、评估桥梁安全状态。可见,数据处理是桥梁监测分析关键环节。另外,在传感器或数据传输设备的采集数据过程中,由于外部环境和人类操作等因素的影响,使传感器采集的数据在分布图上表现出较多的信号毛刺、跳点,此类干扰信号会影响监测项目分析。为减少外界因素对数据的影响、降低数据分析的难度,常采用数字平均的方法对数据进行平滑处理。经过平滑处理后的数据更能凸显出长期变化趋势,便于观察和总结。常用的传统数据平滑处理方法有滑动平均法(MA平滑)[4]和五点三次平滑法(五三平滑)[5]。但传统的平滑方法存在处理方法过粗暴、不易识别异常点等缺陷,因此,高效的平滑滤波方法亟待提出。本文提出基于SG平滑-小波降噪方法,相比传统的信号平滑方法,以期能够显著提高信噪比、降低均方根误差。

1 方法及原理

1.1 Savitzky-Golay平滑

Savitzky-Golay(SG)平滑滤波由Savitzky和Golay[6]在1964年首次提出,它是一种基于局部多项式,通过移动窗口进行最小二乘拟合的滤波平滑方法。该方法很大程度上在保留原数据信息的同时,还能体现较好的平滑效果。目前国内外的学者主要应用在地理信息[7-8]、光谱图像[9-10]上。如文献[7]基于SG滤波算法进行了长时间序列地表温度数据的重建研究,文献[9]提出一种自适应层进式SG平滑滤波算法对光谱进行滤波处理。基于SG滤波在数据平滑上的优势,将与传统的滑动平滑法、五点三次平滑进行对比。SG的平滑过程为

(1)

1.2 小波降噪

由于桥梁结构常常受到行车荷载和环境因素等多方面耦合作用影响,且数据传输过程中存在不可避免的信号质量损失,导致时域数据中包含大量的噪声,因此,需要对数据进行降噪处理。常用的数据处理方法有代表时域分析的傅立叶变换和代表时频分析的小波变换。傅立叶变换不能处理非平稳信号且对时间不敏感,而小波变换可以处理非平稳信号、带强噪声信号[11-12]。小波变换综合了时域和频域分析方法的优点,在时频分析中可以表征信号局部特征,是一种窗口大小固定不变但形状可以改变的时频局部分析方法[13]。文献[14]使用小波阈值去噪对桥梁形变信号数据进行处理,得到去噪信号。

1.3 评价指标

常用的信号评价指标有均方根误差(RMSE)、信噪比(SNR)。信噪比是指信号功率与噪声功率之间的比值,可以通过计算信噪比评价平滑方法的效果[15]。均方根误差是评估信号平滑性能的另一个标准,是判别平滑后的数据与原数据的方差的平方根[16]。文献[17]针对此类问题引用了变异系数定权的方法,用于评价小波分解重构的最佳分层数,变异系数客观反映了指标数值的计算复杂程度。越难实现的指标其变异系数较大,所分配的权重也越大。本文采用T值对小波基函数和分解尺度的选择进行评价,T值的计算首先根据与平滑结果的相关性对各指标进行归一化。

(2)

计算权重后进行线性组合得到复合指标Tj,Tj越小,小波分解重构效果越好。其步骤如下。

(1)计算各指标间的变异系数CVSNR

(3)

(2)计算各指标分配的权重WSNR

(4)

(3)通过线性组合得到复合指标Tj

Tj=WSNR·PSNRj+WRMSE·PRMSEj+Wr·Prj

(5)

式中,σSNR为信噪比序列的方差;μSNR为信噪比序列的均值。

1.4 数据融合

杜家河大桥结构健康监测应变传感器在同一监测位置布置4个,可以取得4组同一位置的监测数据。为减少数据的冗余及提高多源传感器的准确性,引入数据融合技术。基于卡尔曼(Kalman)滤波适合高层数据融合,采用系统模型滤波及允许动态采集环境的特点[18],本文采用卡尔曼滤波对应变数据进行处理。卡尔曼滤波数据融合步骤如下。

(6)

(2)求卡尔曼增益K使得方差最小

(7)

(8)

(9)

2 实例分析

2.1 工程背景

杜家河特大桥是包茂高速公路(G65)西延段K659+500处的一座特大型桥梁,全长678.0 m。桥梁上部结构为(91.5+3×165+91.5)m预应力混凝土连续刚构体系,下部结构为重力式桥台、薄壁桥墩,钻孔灌注桩基础。主桥结构的动态挠度监测采用GSTP-DM-ST型激光位移计监测,通过测量主桥中跨部位的横向、竖向的动态位移变化实现对中跨动态挠度的监测。如图1所示,在主桥箱梁内部左、右两幅中跨L/2处安装靶标,在临近的桥墩部位安装激光器,左右两幅分别布设2个监测点。

图1 布点示意(左幅)

利用GSTP-YC11型压差式小型化静力水准仪、液体静力水准测量分析主桥结构的静态挠曲,并通过测量箱梁内各连通管液面的变化量Δh计算结构的挠曲[19]。在箱梁内部,边跨L/2,主跨L/4、L/2、L3/4,主墩墩顶各设1点,左右两幅分别布设15个监测点。在每幅桥梁端部桥墩处布设1个基准点,杜家河特大桥连通管及测点布设如图2所示。

选用GSTP-FBG300型表贴式光纤光栅式应变计,监测大桥结构典型断面的应变,应变计布设于主桥梁体内,分别位于边跨和主跨L/2断面和边跨桥墩处,大桥全桥左右两幅共计布设14个监测断面,每个断面布设4支应变计,总共56支,测量其顺桥向应变。

对于主桥结构典型裂缝,采用新型导电涂料裂缝监测技术对裂缝宽度变化进行监测,灵敏度为0.01 mm。在箱梁内部寻找10条代表裂缝,覆盖主要裂缝发展区域。对主桥裂缝共布置10条裂缝计进行监测,其中在大桥右幅的R2断面安装2条,R3断面安装4条,大桥左幅的L2、L3断面各安装1条,L4断面安装2条。

2.2 数据分析

2.2.1 信号平滑

分别采用SG平滑、MA平滑及五三平滑对激光位移计、静力水准仪、应变计及裂缝计数据进行平滑处理,如图3所示,对比了4种传感器的3种平滑效果。碍于篇幅只举例分析激光位移计、裂缝计的部分传感器数据平滑说明。激光位移计信号评价指标SNR、RMSE计算值见表1。由表1可知,以JGX-1的平滑指标值为例,SG平滑的SNR分别高于MA平滑和五三平滑23%和22%;其RMSE值优于MA和五三平滑约41%。其他激光位移计中SG平滑效果也优于MA和五三平滑。因此,后续的分析将使用SG平滑后的数据。

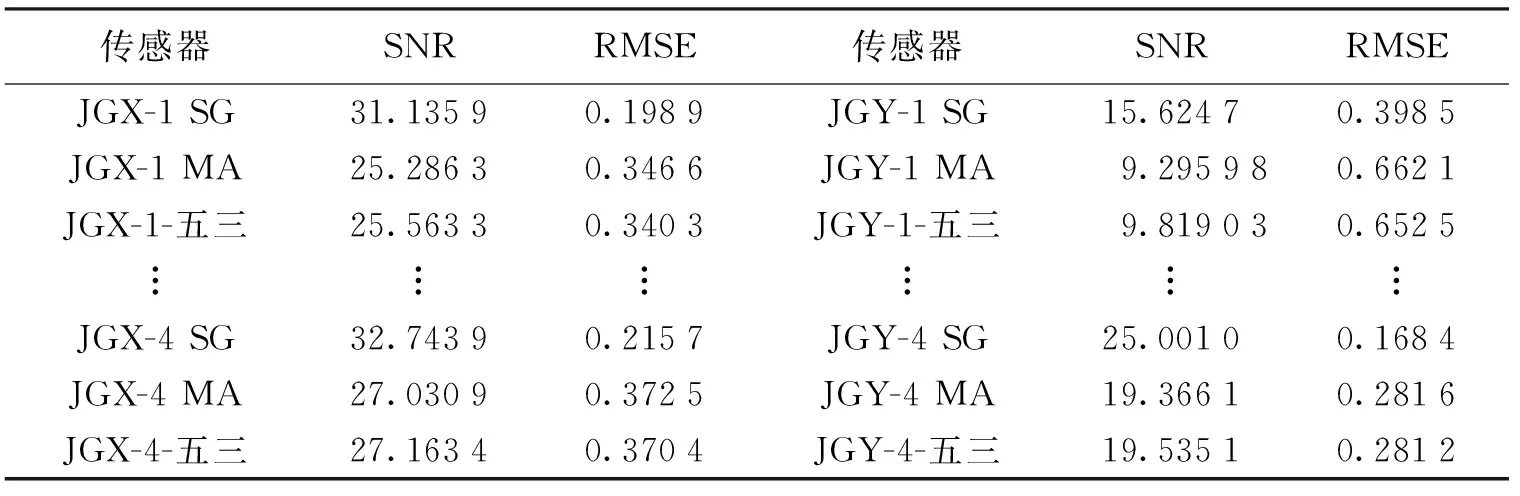
表1 激光位移计平滑评价指标

图3 4种传感器单个数据平滑

2.2.2 小波降噪

在小波降噪中,小波基函数和分解尺度的选择是体现小波降噪的重要参数。选取合适的小波基函数和分解尺度对降噪效果有巨大差异。

2.2.2.1 选择小波基函数

选取小波基函数Haar、coif1-4、db5-9、sym3-7对4种传感器数据进行小波分解重构,用复合评价指标T量化不同小波基函数的降噪效果。如图4所示。对于激光位移计,coif4的T值最小。重复其他激光位移计分解,得到coif4作为激光位移计小波分解的小波基函数。相同的,分别选取sym7、db5和db9作为静力水准仪、裂缝计及应变计数据分解重构的小波基函数。

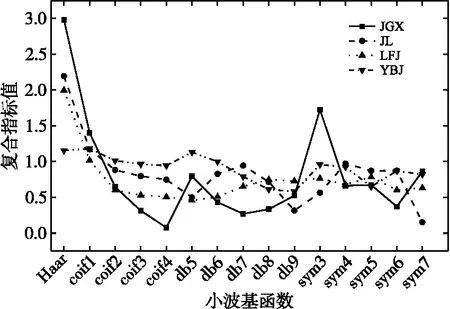
图4 不同小波基函数降噪评价指标

采用静力水准仪小波分解重构时的3种信号评价指标,对选取sym7作为最优的小波基函数进行验证。如图5所示,信噪比最高的为sym7,且其均方根误差是最低的,而在平滑度上略高于db8。综合信噪比、均方根误差及平滑度选出sym7作为小波基函数进行小波分解重构。可见复合指标T的评价与单一指标评价一致。

图5 静力水准仪小波基函数评价情况

2.2.2.2 选择小波分解尺度

小波分解尺度(层数)的选择也是影响小波降噪的重要因素。分解尺度过高,会过滤局部的响应信号;分解尺度过低,则会保留部分噪声,使得降噪过程未达到较好的效果。使用上述不同传感器确定的最佳小波基函数分别进行9层小波分解,并使用复合指标T值对每层分解后的信号进行量化评价,见表2。激光位移计、裂缝计、应变计的分解尺度均为3层效果最好,而静力水准仪需要分解5层方能达到最优去噪效果。

表2 4种传感器不同分解尺度的复合指标T值

以裂缝计小波分解重构过程为例进行说明。由表2可知,裂缝计分解尺度3的信号评价指标T最小。如图6所示,图6(a)分解3层较为合理。即没有分解1—2层的留有部分噪声,也没有分解4—5层的过滤局部响应信号。因此,3层是裂缝计的最佳分解尺度。图6(b)给出了原始信号与分解尺度2、3、4的功率谱密度估计。可以看出,分解尺度3较分解尺度2过滤了大于100 Hz局部微弱的噪声信号,较分解尺度4保留了60～80 Hz低频响应信号。因此,3层是裂缝计信号小波降噪的最优分解尺度。

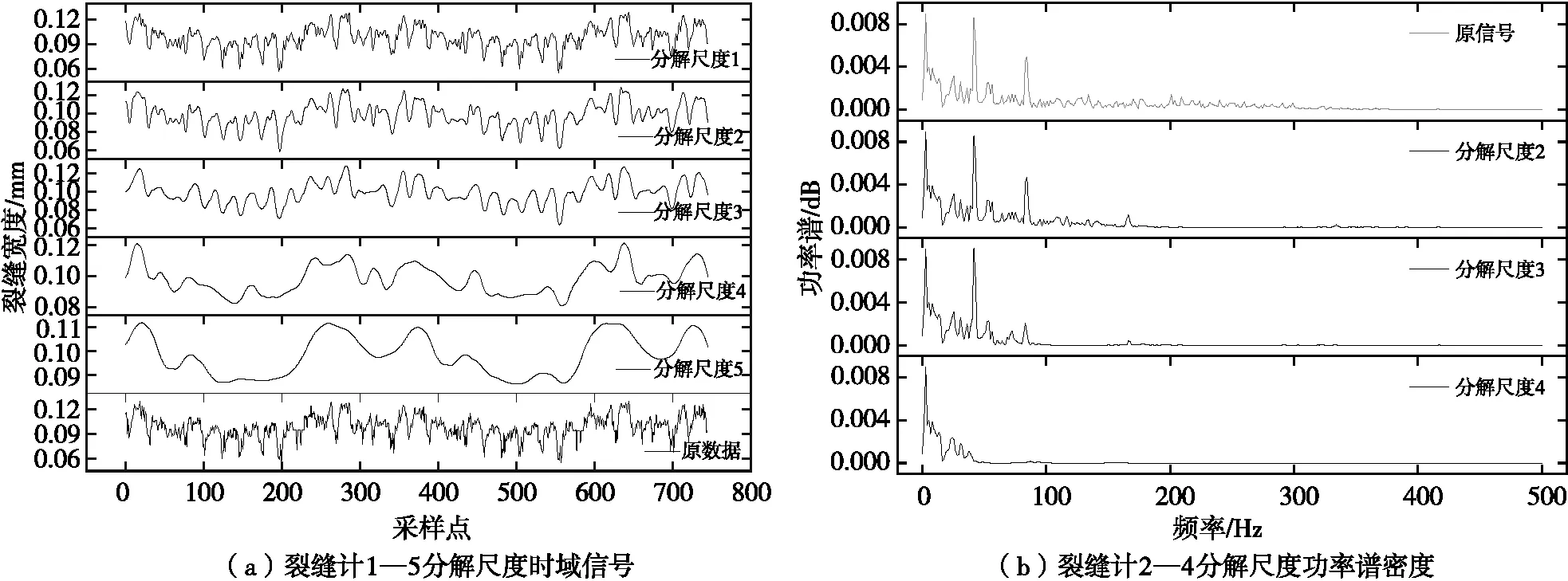
图6 激光位移计缺失值分析

2.2.2.3 小波分解重构降噪

通过已选择的小波基函数和最佳分解尺度参数,将原始信号分解到对应的小波系数。本文选用阈值折中函数对小波系数进行阈值化处理,将阈值化处理后的小波系数进行重构,得到小波去噪后的信号,完成降噪过程。

选取前期处理后的JGX-1数据,分解层数为3层,小波基函数选择coif4。分解重构效果如图7所示,分解信号从上到下的5条曲线分别为JG-1噪声信号层D1、D2、D3,降噪信号A层及原始信号S层,且有S=A+D1+D2+D3+AV,AN为舍弃的低频近似系数部分。在数据采集点15 000、38 000时,原信号突然上升,在D1、D2、D3层中出现奇异值点。而在采集点11 000,20 000及24 000时,原信号存在上升趋势,噪声层D1、D2、D3层出现较强的噪声。判断存在较大的荷载,使得结构发生较大挠度变化。此外,可以看出原信号的其他极值点也存在此类情况,表明降噪效果较好。

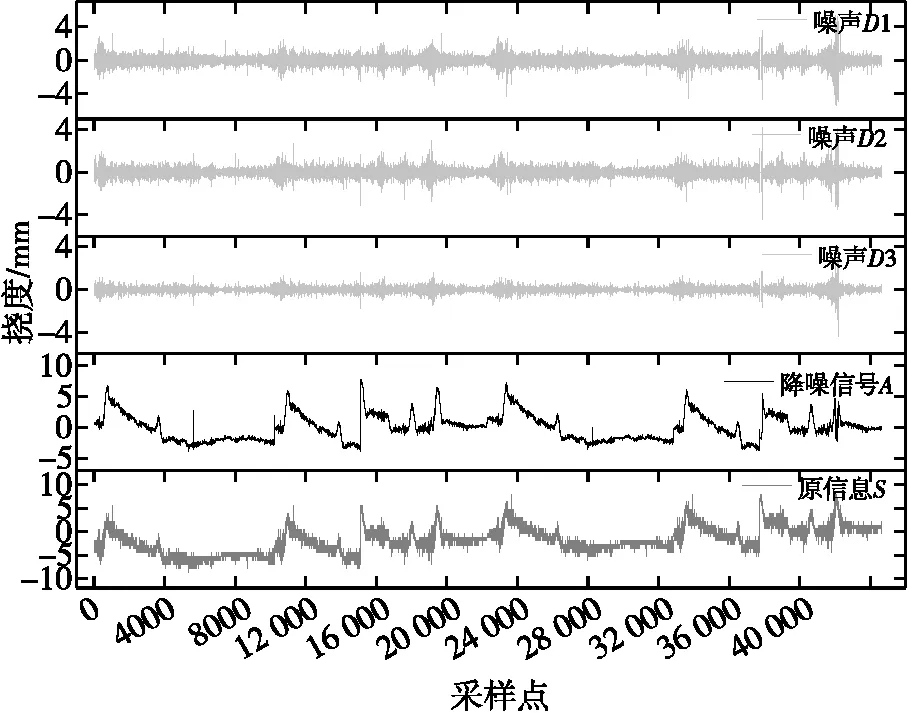
图7 激光位移计JGX-1分解重构效果

2.2.2.4 降噪对比

分别对监测数据源信号和平滑后的信号进行小波降噪,并用信号评价指标SNR、RMSE进行量化。如图8所示,激光位移计数据经过SG平滑小波降噪得到的SNR比仅经过SG平滑或仅小波降噪高。在均方根误差上,组合效果也较单一处理数值低,表征组合效果比单一效果要好。

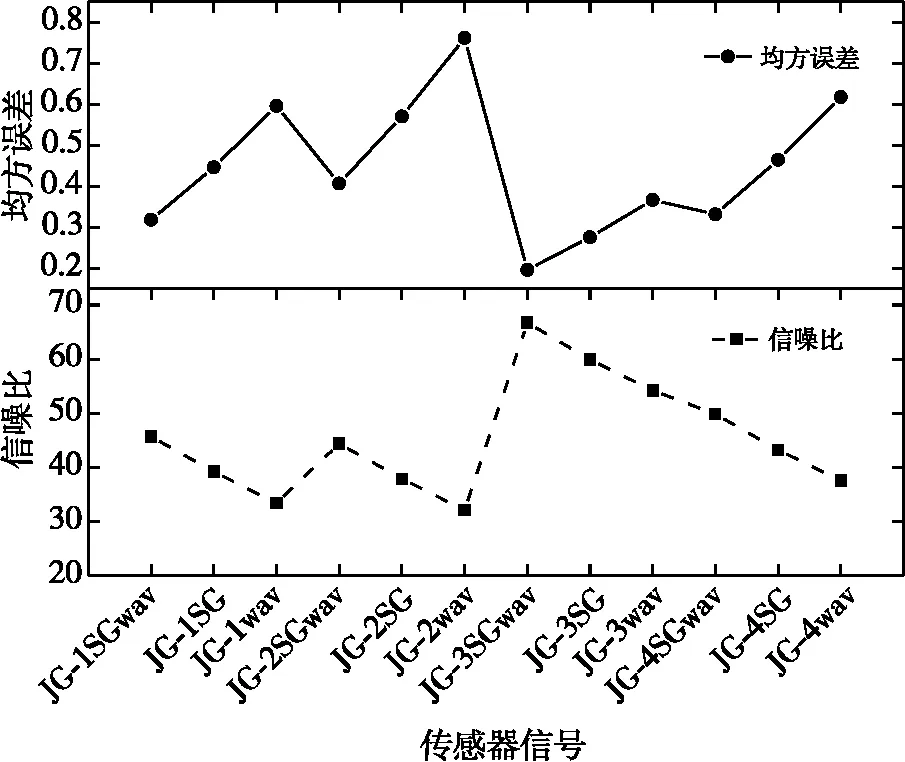
图8 激光位移计JGX-1组合处理评价量化

2.2.3 数据融合

对同一监测点4个应变计同步采集信息的冗余情况,使用卡尔曼滤波对每个监测点的4个传感器数据进行数据融合。分别将上述预处理后的应变计原数据及其小波降噪数据同时进行数据融合。首先通过数据的误差平方计算卡尔曼增益,然后采用线性组合得到估计值,最后在得到估计值后进一步更新卡尔曼增益。基于数据局限,选取1—3号应变计数据进行可视化说明,如图9所示。原数据与小波降噪数据变化走向趋于一致,表明卡尔曼滤波融合效果较好。

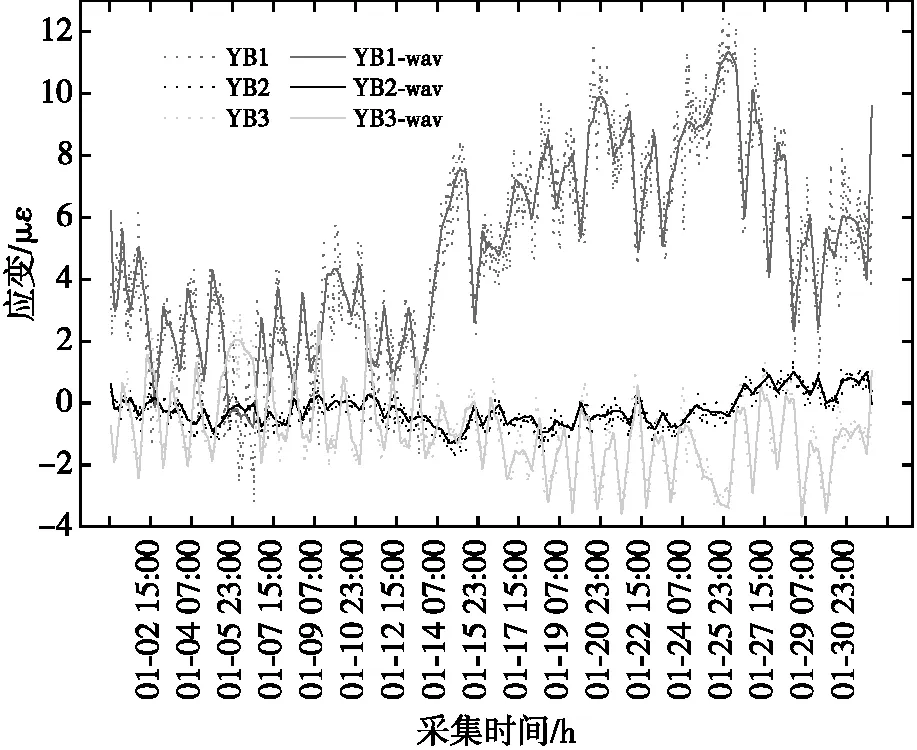
图9 应变计1—3数据融合

为验证融合数据的有效性,使用Monte Carlo对4组传感器与融合数据进行仿真[20],并采用均方根误差(RMSE)作为算法的评价指标[21]。其中不同传感器的均方根误差RMSEp的计算过程为

(10)

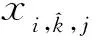
以应变计1-1至1-4及其融合信号为例,通过Monte Carlo仿真500次,误差比较如图10所示。经由卡尔曼滤波后的数据比单个数据的估计更加稳定、可靠且精度更高,仿真结果验证了使用卡尔曼滤波数据融合算法的稳定性和准确度。

图10 1号应变计融合前后误差比较

3 结 论

本文依托杜家河大桥健康监测数据,采用SG平滑-小波降噪方式,分别对激光位移计、静力水准仪、应变计及裂缝计4种传感器进行了处理分析。使用复合指标T对不同的小波基函数及分解尺度进行评价,得到以下结论。

(1)引入地理信息和光谱图像方面平滑效果较好的Savitzky-Golay滤波,经过4种传感器的数据平滑效果检验,得出SG平滑效果始终优于传统的滑动平均法和五点三次平滑。

(2)选取常用的小波基函数Haar、coif1-4、db5-9、sym3-7对4种传感器数据进行小波分解重构,用复合评价指标T量化小波分解重构的降噪效果。得出不同传感器数据进行小波降噪时选择的小波基函数和最佳分解尺度是不同的,这是基于传感器采集特点和采集方式不同。

(3)使用组合SG平滑-小波降噪的方法比单一的SG平滑或小波降噪效果好。

(4)对杜家河特大桥同一监测位置的4个应变计信号进行数据融合处理,并用Monte Carlo仿真验证其准确性,得出卡尔曼数据融合算法的有效性。

基于杜家河大桥的健康监测数据进行处理分析,总结出针对不同传感器的不同信号处理方式。可为桥梁结构健康监测数据的相关传感器提供了借鉴,此外,引入的Savitzky-Golay法在4种传感器的数据平滑和滤波上均有较好的结果,可为健康监测数据、传感器数据平滑滤波提供参考。