基于北斗卫星导航系统的地下车库深基坑沉降监测与分析

黄 鑫,张继文,于永堂,3,徐传召,张 率,曾 涛,王竞革

(1.西安建筑科技大学土木工程学院,陕西 西安 710055; 2.机械工业勘察设计研究院有限公司陕西省特殊岩土性质与处理重点实验室,陕西 西安 710021; 3.中联西北工程设计研究院有限公司,陕西 西安 710077)

地下空间开发利用已成为我国城市建设和城市更新的重要组成部分,并呈现出大规模、高速度、多层次和多类别的发展趋势。竖井式地下车库具有占地面积小、土地利用率高等优势,适用于解决城区停车难的问题,也符合城市地下空间开发利用的要求。但竖井式地下车库同时具有小面积开挖、大深度掘进的工程特点,在施工过程中会产生较大深基坑,存在垮塌、周边沉降等安全隐患[1-2]。为了保障建筑物施工过程中深基坑本身及周围建构筑物的安全,需要对深基坑周边的地表沉降进行持续监测。目前,地表变形监测多采用常规大地水准测量方法,主要包括三角测量[3]、几何水准测量[4]和交会测量[5]等方法。该类方法的主要特征是理论和方法成熟,监测费用相对较低,但存在监测历时长、劳动强度高、不能实现自动化监测、无法及时进行风险预警等缺点。基于BDS(BeiDou Navigation Satellite System)采用载波相位差分定位技术开发的变形监测系统(BDS变形监测系统)具有全天候运行、数据采集频率高、自动化程度高、布测区域广的特点[6-7],能有效弥补人工水准监测的不足,已被应用于边坡变形监测[8-9]、高填方地表变形监测[10-11]及其他变形监测工程[12-14]。目前国内关于北斗变形监测技术的应用研究主要是针对范围宽广、无遮挡、施工完成后工程场地的变形监测,而对范围狭窄、有遮挡、施工过程中的场地变形监测研究鲜有报道,后者受施工环境的干扰大,其适用性与监测效果尚缺乏定量评估。

本文利用BDS变形监测系统对西安市东郊某地下立体车库施工及工后期的沉降变形进行持续监测,利用小波降噪方法对原始数据进行降噪处理,分析BDS变形监测系统监测值与水准监测值的相对误差情况,并对该场地的最终沉降量进行预测,以期为BDS变形监测系统的工程应用提供参考。

1 BDS变形监测系统概况

1.1 系统组成

BDS变形监测系统由硬件系统和服务器软件两部分组成。

1.1.1 硬件系统

硬件系统的框架如图1所示,主要包含6个功能模块:数据采集与解析模块、三维坐标解算模块、北斗接收板模块、电源模块、无线通信模块。

图1 嵌入式硬件系统设计

(1)数据采集与解析模块:采用ARM7处理器,负责对采集到的定位信息、载波相位监测值及北斗导航卫星的位置信息进行解析,并传送给三维坐标解算模块及无线通信模块。

(2)三维坐标解算模块:采用ARM11处理器,主要运行北斗差分定位核心算法,实时解算载体的三维坐标。

(3)北斗接收板模块:采用射频和基带一体化的SOC芯片型导航高精度卫星信号处理模块(司南导航K706板卡),负责接收、处理北斗卫星监测数据。

(4)电源模块:采用5～8 V供电,使用的电源芯片为TPS54383芯片,负责为整个系统提供稳定的电源。

(5)无线通信模块:采用的是众山ZSD14104GDTU,负责将三维坐标解算模块解算的坐标数据通过GPRS无线网络发送到上位机。

1.1.2 服务器软件

服务器软件是一个可视化的远程监测平台,一方面能动态显示接收到的RTK定位结果,另一方面能通过大量的原始数据进行静态相对定位解算。主要功能包括CSocket网络通信、动态数据解析、静态数据解算、MySQL数据库存储、监测站变形监测信息等模块,可实现对原始数据的记录、查询等功能,实现对监测数据的高效管理、分析和处理。

1.2 定位解算方法

(1)双差监测方程的建立。如图2所示,假设安置在基准站和监测站的两个北斗接收机于t1历元和t2历元分别对卫星P、Q、M、N进行同步监测,则可以得到t1历元和t2历元各8个独立的载波相位监测值,对应8个载波监测方程式,对8个方程式进行两次作差可得载波相位双差监测方程式。

(2)模糊度浮点解的求解。各种利用载波监测值的随机误差均由模糊度、基线向量或位置等其他因素组成,假设随机误差服从正态分布,利用最小二乘法即可得各未知数在实数域的最优估值,此解即为浮点解。

(3)固定双差整周模糊度。利用整数最小二乘法与LAMBDA结合的方法寻找模糊度整数解候选值,并对模糊度整数解候选值进行确认检验,得到定位未知数的整数解。

(4)静态定位解算。求解出精确的基线矢量,并结合基准站的已知坐标得到监测站的高精度坐标。

2 深基坑沉降监测

2.1 工程概况及监测点位布设

本次利用BDS变形监测系统对西安市东郊某地下车库深基坑工程的地表沉降变形进行了持续监测。该地下车库圆形深基坑的设计直径为18.9 m,深度为8.7 m,车库主体顶部距离地表约0.9 m。工程场地的原始地貌属于渭河一级阶地,场区主要地层自上而下分别为:0.0～0.9 m为素填土;0.9～4.8 m为黄土状土;4.8～5.7 m为粉土;5.7～9.0 m为黄土;9.0～20.0 m均为中砂。为获得地表累计沉降量,在基坑顶部边缘地表设置了4个BDS监测站(B1—B4),每个监测站均相隔一个车位,且在每个车库顶部及车库周边地表设置了水准监测点位(S1—S19),其中S1、S3、S5、S7分别与4个北斗监测站位置对应,监测点位布设如图3所示。

图3 监测点布设

2.2 监测数据分析

本次监测时间为2022年6月20日至9月1日,共计73 d,原始监测数据如图4所示。

图4 累计沉降监测数据

由图4可知,场地累计沉降量随着时间增长而持续增大,监测历时内,B1、B3、B4的累计沉降量分别为101、95.9、89.6 mm,沉降速率分别为0.6、14.3、1.5 mm/d,均未达到稳定状态。由于本次施工场地较为狭窄,施工影响较大,导致B1、B3、B4监测数据均含有噪声,B2监测数据缺失。

3 监测数据降噪处理

根据各测点处监测曲线的走势来看,虽然累计沉降随时间推移大体呈现增长趋势,但由于施工干扰较大,导致监测数据出现较大波动性,难以准确预测最终沉降量,因此需要采用小波降噪法对监测数据进行降噪处理[15]。

3.1 小波降噪原理

小波降噪的原理与步骤如图5所示。首先选定一种小波基函数,对信号进行N层分解,然后对分解得到的各层系数选择一个阈值,并对细节系数作用软阈值处理,最后对降噪处理后的系数通过小波重建得到降噪后的监测信号。

图5 小波降噪原理与步骤

在进行小波降噪时,假设含噪声监测数据数学模型为

Si=S′i+eii=1,2,…,n

(1)

式中,Si为第i期的变形监测数据,它包括真实变形量和确定性噪声;S′i为真实变形量;ei为随机噪声。

此次数据处理利用Matlab中的wavelet工具箱实现具体操作,图5(b)中S表示原始信号,即原始监测数据,此次将原始信号进行5层小波分解,d1～d5分别表示第1～5层分解后的高频信号,a5表示经过5层小波分解后的低频信号,即为有效信息。

3.2 降噪误差评价指标

(1)均方根误差(RMSE)。经过小波降噪后数据和原始数据的均方误差,表达式为

(2)

式中,i=1,2,…,n,为监测期数;Si为原始监测数据;S′i为小波去噪后的监测数据。RMSE值越小表示去噪效果越好。

(2)信噪比(SNR)。信噪比是指信号值和噪声值的比值,比值越高去噪效果越好,表达式为[16]

(3)

式中,Ps、Pn分别表示信号值和噪声值的有效功率。可表示为

(4)

(5)

3.3 不同基函数降噪效果对比

本次分别利用Daubechies、Symlet、Biorthogonal基函数对原始监测数据进行小波降噪分析,得到降噪前后监测数据的对比,如图6所示,降噪效果评价指标见表1。

表1 不同基函数降噪误差分析

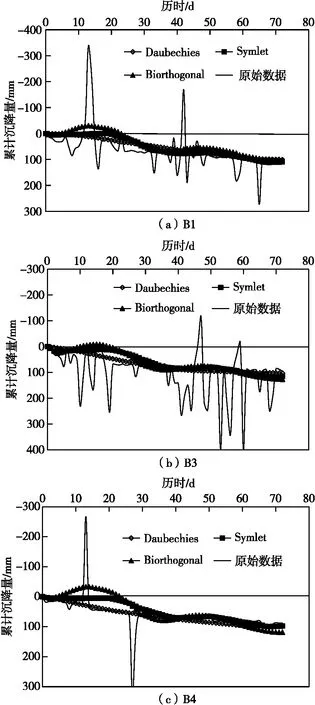
图6 监测数据降噪前后对比

由图6、表1可知,3种分析方法均在很大程度上筛除了原始数据中的噪声信息,处理后的沉降监测曲线走势与原始数据基本一致。其中,Daubechies方法降噪处理后的数据与原数据的均方根误差最小,信噪比最大。

3.4 BDS变形监测系统与水准监测数据的对比分析

经Daubechies方法降噪处理后的BDS变形监测系统监测数据与水准监测数据对比如图7所示,两者相对误差情况如图8所示。

图7 BDS监测值与水准监测值对比

图8 BDS与水准监测值误差情况

由图7—图8可知,两种监测方式均能够反映出地下车库的沉降变化特征,但水准监测法在73 d的监测期内仅采集到了7期地表沉降数据,最大的监测时间间隔为14 d,监测数据完整性较差。BDS变形监测系统为24 h自动化连续监测,监测数据完整性较好,监测曲线较为连续平滑,与水准监测数据的平均误差在5.5%～10.3%以内,其中施工期的相对误差在7.1%～16.2%之间,施工结束后,两者的相对误差减小至2.5%～3.4%。

4 最终沉降量预测

4.1 沉降曲线特征分析

本次工后沉降监测数据共历时17 d,工后沉降监测数据及沉降速率变化规律如图9所示。

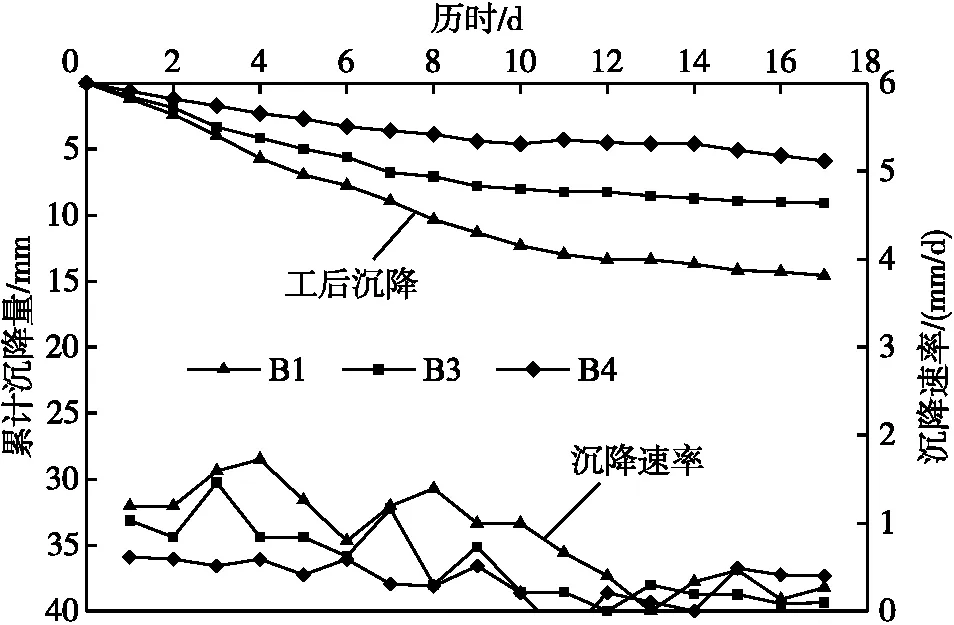
图9 工后沉降量及沉降速率变化规律

由图9可知,随监测时长的增加,工后沉降曲线逐步趋于平缓,但并未出现明显的拐点。在历时17 d后,沉降量最大的监测点B1,累计沉降量为14.58 mm,沉降速率已由最初的1.19 mm/d降低至0.26 mm/d;其次为监测点B4,累计沉降量为8.76 mm,沉降速率已由最初的1.03 mm/d降低至0.22 mm/d;监测点B3累计沉降量最小,仅为5.90 mm,沉降速率已由最初的0.61 mm/d降低至0.40 mm/d。

4.2 沉降预测的回归参数模型

表2 回归参数模型表达式

4.3 沉降预测的效果评价指标

(1)拟合优度评价指标。选取决定系数(R2)作为预测模型拟合优度的评价指标,计算公式为

(6)

(2)预测误差的评价方法。采用平均绝对相对误差(MAPE)、平均预测误差(MFE)指标判定模型外推预测效果。MAPE值能够较好地衡量模型的预测精度,其值越小精度越高;MFE值能较好体现模型的无偏性(如预测值相对于实测值的正负偏差)。计算公式分别为

(7)

(8)

4.4 沉降预测的效果对比分析

场地内各监测点的工后期监测历时均为17 d(每天为1期,共17期实测数据),利用前11期实测数据求解模型参数,后6期实测数据检验模型的外推预测效果。建模参数与预测精度指标统计见表3,建模曲线如图10所示。可知,修正Gompertz模型、对数函数模型的相关系数R2平均值分别为0.993 2、0.966 3,MAPE平均值依次为1.6%、3.7%,MFE平均值依次为0.03、0.40。即修正Gompertz模型的内拟合精度及外推预测精度均优于对数函数模型,且根据图11可知,修正Gompertz模型的内拟合、外推预测的相对误差比较稳定,且均低于7.0%,因此选取修正Gompertz模型作为此次沉降预测模型。

表3 预测模型的回归参数及精度统计

图10 工后沉降监测及预测曲线

图11 修正Gompertz预测误差变化规律

4.5 最终沉降量预测

参考现行《建筑变形测量规范》[17],选取0.04 mm/d的沉降速率为稳定标准。沉降速率表达式为

S′ti=ab·e-e-b(ti-c)-b(ti-c)

(9)

式中,S′ti表示第i期对应的沉降速率。计算系数取值参考表3。

经过计算,该场地B1处将在工后22 d后达到稳定,其工后沉降量为14.8 mm,总沉降量为100.5 mm;B3处将在工后14 d后达到稳定,工后沉降量为4.7 mm,总沉降量为101.5 mm;B4处将在工后16 d达到稳定,工后沉降量为8.7 mm,总沉降量为99.8 mm。3个测点的总沉降量均在100 mm左右,监测期间内未发生明显的差异沉降。

5 结 论

(1)施工干扰会使BDS变形监测系统监测数据产生较大波动,导致难以准确判断场地的变形趋势,需要通过降噪方法予以校正。

(2)利用Daubechies小波降噪方法能有效剔除由施工干扰产生的噪声信息,降噪后的监测数据与水准监测数据的相对误差为5.5%～10.3%。

(3)利用修正的Gompertz模型预测该场地B1、B3、B4的稳定时间分别为22、14、16 d,总沉降量分别为100.5、101.5、99.8 mm,场地在监测期间内未发生明显差异变形。