无人机与卫星影像匹配的相似性逼近算法
罗卿莉,张书缤,陈 相,魏钜杰
(1.天津大学精密测试技术及仪器国家重点实验室,天津 300072; 2.中国测绘科学研究院,北京 100036)
影像匹配导航技术是一种在全球卫星导航系统失效情况下的高精度导航技术。无人机影像匹配定位是将无人机获取的影像与带地理坐标的卫星影像进行匹配,建立无人机与卫星影像的映射关系,从而获取无人机影像对应的地理坐标信息。建立无人机与卫星影像间的匹配关系是进行无人机影像匹配定位的关键。
在影像匹配方法中,模板匹配是最基本的方法[1]。文献[2]提出MAD(mean absolute differences)算法,该算法匹配精度较高,但对噪声较敏感。文献[3]提出NCC(normalized cross correlation)算法,提高了匹配精度,但速度较慢,应用受到限制。
模板匹配利用影像的全局信息进行计算,速度慢,且不适用于具有尺度变换、旋转变换等类型的影像匹配。为了解决上述问题,有学者提出了基于局部信息的特征匹配算法。该算法的特征包括点特征[4-5]和线特征[6-7]等。基于点特征的影像匹配方法为,提取影像的特征点,将特征点邻域内的特征信息作为特征点的描述向量,通过描述向量在两幅影像中搜索匹配的特征点对,从而确定两幅影像的映射关系。具有代表性的基于影像特征点的匹配方法包括SIFT[8]、SURF[9]和ORB[10]等。其中,SIFT对尺度、旋转等变换具有不变性,在多种场合都有很好的稳健性。
无人机与卫星影像匹配时,无人机影像拍摄视角的不同会造成影像倾斜。文献[11]提出基于仿射变换的ASIFT算法,有效地解决了影像倾斜拍摄造成的形变问题,但算法的复杂度较高。文献[12]提出使用POS数据获取不同视角下影像仿射变换的单应性矩阵,改进了ASIFT算法中的视角模拟,大大降低了算法的计算时间。文献[13]针对宽基线城市影像匹配的问题提出局部几何结构(local geometrical structure,LGS),该方法能较好地解决大视差情况下的影像匹配。
无人机与卫星影像匹配的另一难点为,难以对影像空间分辨率差异较大的影像进行正确匹配。文献[14]提出一种渐进的匹配策略,将具有大尺度差异的两幅影像在对应的尺度中进行匹配,提高了匹配率。文献[15]提出基于分块搜索的匹配策略,但采用暴力搜索,效率偏低;文献[16]将算法进行改进,提升了匹配速度,但无人机影像空间分辨率进一步提升的情况下难以得到有效的匹配结果。
无人机与卫星影像的空间分辨率差异较大(14倍)时,现有算法存在匹配对正确率低、无法进行有效匹配的问题。因此,本文提出无人机与卫星影像匹配的相似性逼近算法,即通过对下采样后的无人机影像进行高斯滤波,以提高无人机和卫星影像的尺度相似性,达到缩小两者之间的空间分辨率差异、提高匹配正确率的效果。
1 研究方法
本文相似性逼近算法包含3个主要步骤:无人机和卫星影像预处理(分别对应影像下采样和影像分块)、基于相似性逼近的无人机影像优化、影像匹配搜索。算法整体流程如图1所示。

图1 算法整体流程
1.1 无人机和卫星遥感影像预处理
由于卫星影像覆盖范围大,卫星影像中与无人机影像不相关的区域存在大量噪声点,对匹配对的搜索造成了干扰,因此难以获取正确的匹配点对。该问题可通过对卫星影像进行分块处理解决。图2(a)为由谷歌卫星影像导出的20级影像,位于天津市蓟州区。影像大小为4640×2700像素,空间分辨率为0.42 m。将该卫星影像分割为16×9块影像,每块大小为290×300像素。分割后的影像如图2(b)所示。

图2 蓟州区卫星影像
由于无人机与卫星影像具有较大的空间分辨率差异,因此即使在相同的特征点上,基于特征点邻域内像素计算得到的描述子也具有较大差异,直接使用现有的匹配算法难以得到正确的匹配结果。针对该问题,本文对无人机影像进行了下采样,将无人机影像的空间分辨率RUAV与卫星影像的空间分辨率RSAT的比值α作为无人机影像下采样的倍率,通过缩小无人机影像,使两者的空间分辨率处于相近的尺度,从而确保相同位置的特征点的描述子具有近似的结构。
1.2 无人机影像的相似性逼近优化
下采样后的无人机影像与卫星子块影像存在清晰度的差异,本文基于相似性逼近的优化方法采用高斯函数减少两者的频谱差异。二维的高斯函数频率域的表达式为
H(u,v)=e-D2(u,v)/2D02
(1)
式中,D(u,v)为距频率矩形中心的距离(距离小称为低频,距离大称为高频);D0为中心拓展度的度量。
图3为不同D0值下的滤波器的剖面图。可以看出,高斯函数在低频处的幅值接近1,随着频率的增大,幅值发生衰减。
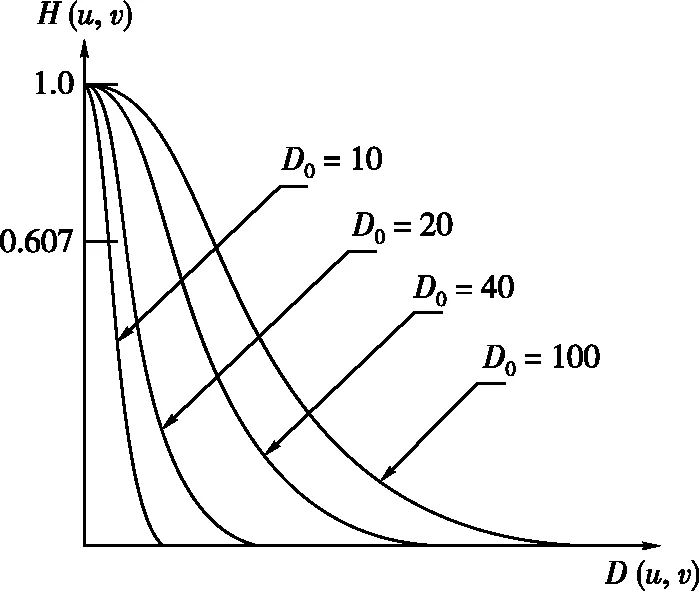
图3 不同D0下滤波器的剖面图
试验区卫星影像子块与下采样后的无人机影像如图4(a)、(b)所示。卫星影像空间分辨率较低,视觉较模糊;无人机影像空间分辨率较高,视觉较清晰。为了探究无人机和卫星影像之间的尺度差异,对两幅影像分别进行傅立叶变换,得到其频谱分布,如图4(c)、(d)所示。在卫星子块影像的频谱中,水平横轴和纵轴方向呈现出明显的峰值,其他响应值大致位于Z轴坐标值5的位置。在无人机影像的频谱图中,水平横轴和纵轴能够观测到峰值,但其余频率分量的响应值普遍较高(位于Z轴坐标值8的位置),使得峰值处并不明显。图4(d)经相似性逼近的优化算法处理后,得到图4(e)。图4(f)为无人机影像在优化算法处理前后的差值图。由图4(e)可以看出,经过优化算法处理后的无人机影像频谱也呈现明显的峰值,且响应值下降至Z轴坐标值5的位置。
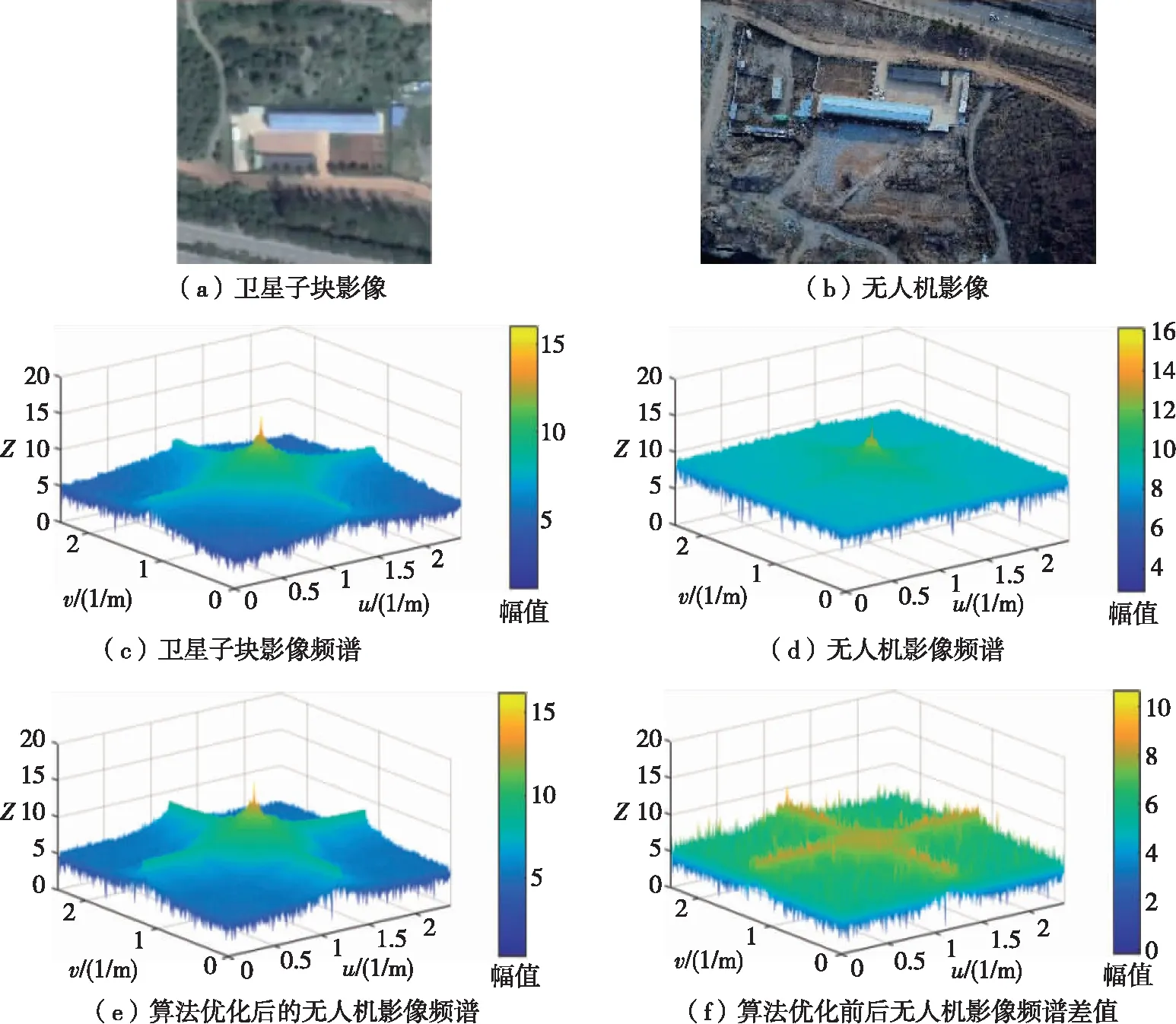
图4 卫星影像和无人机影像与对应的频谱
为了进一步评估本文方法有助于缩小无人机影像和卫星遥感影像之间的尺度差异,利用峰值信噪比(peak signal noise ratio,PSNR)和结构相似性(structural similarity,SSIM)指标,分别对试验区无人机和卫星影像进行算法优化前后的相似性估计。
为了减小由于拍摄时间不同存在的季节性(如辐射变化、植被状态变化等)影响,裁剪相同的建筑区域影像进行分析,如图5所示。以卫星影像为基准,通过PSNR和SSIM指标对无人机和卫星影像的相似性进行评估。具体指标见表1。传统算法的PSNR值为16.52,SSIM值为0.38;算法优化后的PSNR值提升至17.51,SSIM值提升至0.59。结果表明,经本文算法优化后,无人机与卫星影像的相似度有较明显的提高。
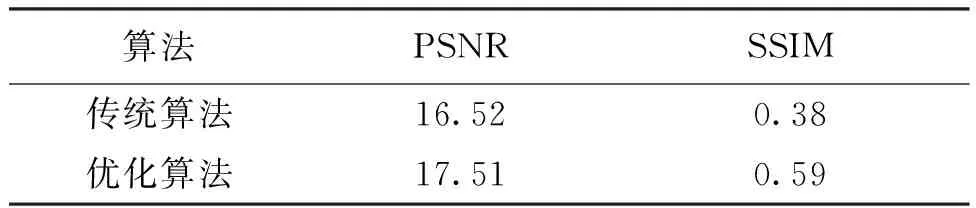
表1 无人机与遥感影像的相似度估计

图5 裁剪区域对比
1.3 无人机和卫星影像匹配流程
将优化后的无人机影像依次与卫星子块影像进行SIFT特征点匹配,通过评价指标筛选出最优的卫星子块,获取最终的匹配结果。评价公式为
(2)
式中,Di为匹配点对的描述子的距离;n为匹配点对的组数。匹配点对的描述子距离越小,组数越多,评价指标越小,匹配程度越高。
2 试验与结果分析
2.1 确定高斯滤波参数
高斯滤波参数包括高斯核的大小及标准差(D0)。在标准差固定为2的情况下,使用不同大小的高斯核进行对比试验,分别比较不同情况下影像的PSNR、SSIM、匹配对的正确率(correct match ratio,CMR)及无人机影像特征点个数N,结果见表2。

表2 高斯核大小与影像评价指标的关系
由表2可以看出,采用相似性逼近优化算法后,PSNR值和SSIM值都有较大提升。但提取的特征点个数N随高斯核的增加而减少。高斯核大小为5时,特征点N为436,其匹配正确率CMR最高,为80%。高斯核大小为7和9时,特征点数N下降,其匹配对的正确率也逐渐下降,分别降至50%和25%。
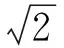
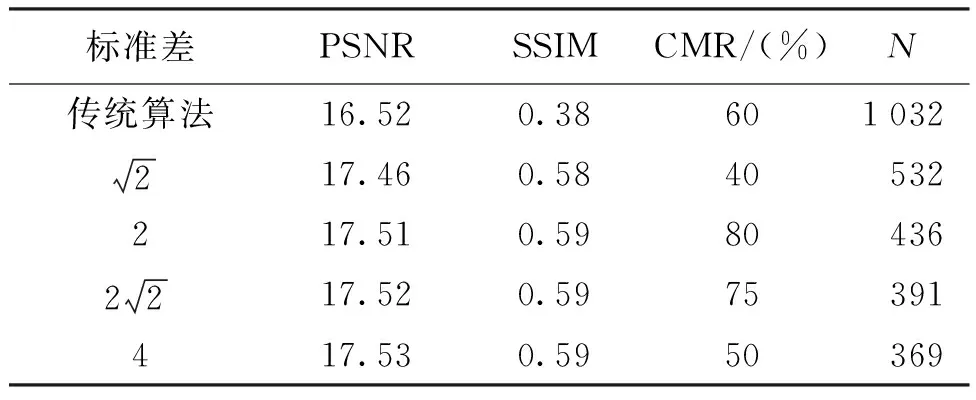
表3 标准差与影像评价指标的关系
随着高斯核大小的增加与标准差的增大,PSNR值和SSIM值均得到提高。高斯核与标准差过大时PSNR值和SSIM值增长缓慢甚至不变,同时会导致影像边缘像素缺失,进而使得特征点个数N减少及描述子方向偏移,匹配对正确率下降。因此,综合评价指标结果,后续试验中设置高斯核大小和标准差分别为5和2。
2.2 匹配试验
为了验证本文算法的有效性,对文献[16]的算法加入相似性逼近优化算法,并进行对比,使用CMR对试验结果进行量化评价。如表4和图6所示,使用文献[16]的算法进行匹配,匹配对的正确率均相对较低。如影像1,匹配对组数M为5,正确匹配对的组数R为3,匹配对正确率CMR为60%。经本文算法优化后,匹配对的正确率明显提升。影像1匹配对的正确率由60%上升至80%。结果表明,本文算法能够有效提升尺度差异较大的无人机与卫星影像的特征点匹配对数及匹配正确率。

表4 无人机影像匹配结果

图6 匹配结果对比(红色线代表正确匹配对,蓝色线代表错误匹配对)
3 结 语
本文提出了一种无人机与卫星影像匹配的相似性逼近算法。该算法首先分析了具有较大空间分辨率尺度差异(14倍)的两者的频谱差异,利用高斯滤波减小无人机和卫星影像的差异,从而提高两者的尺度相似性。通过该优化算法,无人机与卫星影像的匹配效果得到了明显提升,匹配正确率CMR由平均58%提高至平均87%,提升了29%。试验结果证明了本文算法的有效性。

