两种北斗卫星精密星历外推方法的精度分析

申少飞,雷伟伟,李振南,2,马晨阳

(1. 河南理工大学测绘与国土信息工程学院,河南 焦作 454003; 2. 中国科学院精密测量科学与技术创新研究院,湖北 武汉 430077)

北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)是由中国自行研制、面向全球的卫星导航系统[1]。2020年6月23日,北斗三号最后一颗全球组网卫星发射成功,标志着北斗卫星导航系统正式完成全球组网,其在设计性能上优于俄罗斯的GLONASS,且与GPS性能相当[2]。北斗卫星的定位精度可达分米级和厘米级,在定位过程中需要通过卫星精密星历获取卫星的坐标信息[3]。GNSS服务组织提供的精密星历采样间隔一般为15或5 min,通常接收机的采样间隔为30、15或1 s[4]。为获取时间间隔更短的连续历元的卫星坐标,通常采用插值和拟合的方法[5]。

常用的插值和拟合方法有拉格朗日插值法、牛顿插值法、切比雪夫多项式拟合和勒让德多项式拟合[6-10]。只要选取合适的时段和阶数,插值和拟合精度都能达到厘米甚至毫米级,完全能满足精度要求。但国际全球卫星导航系统服务(International GNSS Service,IGS)仅提供一天中00:00:00—23:45:00的星历坐标。因此,为了得到23:45:00—24:00:00的星历坐标有两种方法:第1种是将当天和第2天的精密星历连接,采用插值或拟合的方法求取对应的星历坐标;第2种方法是依据当天的星历数据直接进行坐标外推求得星历坐标[11]。采用第1种方法,当两天中某个时段的精密星历中断时,得出的结果精度不高,因此,通常选择第2种外推方法。采用第2种方法要设法提高星历外推精度。文献[12]采用滑动式拉格朗日多项式插值和三角函数对IGS精密星历进行外推,三角函数有效利用了卫星在空间运动的特点,外推精度明显优于滑动式拉格朗日插值,且三角函数在6阶时外推效果最优,小于滑动式拉格朗日插值的9阶。文献[13]运用拉格朗日插值、切比雪夫多项式拟合和三角函数对GPS精密星历进行内插和外推,结果表明3种方法内插精度大致相同,但三角函数的外推精度明显优于另外两种方法。文献[14]利用广义延拓法对GPS精密星历进行内插和外推,并与拉格朗日插值法的结果进行对比,结果表明广义延拓逼近法插值精度小于5 cm,在外推30 min后依然能保持较高精度,优于拉格朗日插值法。文献[15]绘制11阶多项式和9阶三角函数在23:00—24:00时间段的外推图像,结果表明三角函数在24:00外推误差小于10 cm,精度远高于多项式外推结果,进一步验证了三角函数具有良好的外推能力。

以上只是针对GPS精密星历的轨道坐标外推研究,而关于北斗卫星研究的较少。不同于GPS,BDS是由地球静止轨道(geostationary earth orbit,GEO)、中圆地球轨道(medium earth orbit,MEO)和倾斜地球同步轨道(inclined geosynchronous satellite orbit,IGSO)3种不同轨道的卫星星座组成[16]。本文采用三角函数插值法和广义延拓逼近法,分别对采样间隔为15 和5 min的北斗卫星精密星历进行5 min间隔外推,并与原始精密星历作差后进行精度分析,对比两种方法的外推能力。

1 两种精密星历轨道坐标外推模型

1.1 三角函数插值多项式

BDS卫星绕地球运动过程中是有规律性的,呈周期性变化。三角函数插值法能够很好地反映卫星的这种周期性运动规律,使插值精度更高。但卫星在地固坐标系下运动时,精密星历引入了地球自身运动,影响卫星的运动规律。而在惯性坐标系下,卫星运动更能反映卫星本身的运动特点,更有规律。运用三角函数插值法对卫星精密星历进行外推,首先将精密星历的坐标由地固系转换为惯性坐标系,转换方程[17]为

(1)

其中

M=R2(-xp)R1(-yp)

E=R3(GAST)

N=R1(-ε-Δε)R3(-ΔΨ)R1(ε)

P=R3(-90-ZA)R1(θA)R3(ξA)

式中,(x,y,z)为以CTP为指向的协议地球坐标;(X,Y,Z)为协议天球坐标系;M、E、N、P分别为极移旋转矩阵、旋转春分点时角、章动旋转矩阵、岁差旋转矩阵;xp、yp为极移分量;GAST为格林尼治时角;Δε、ΔΨ、ε分别为交角章动、黄经章动、黄赤交角;ξA、ZA、θA为岁差参数;R1、R2、R3为旋转矩阵,其表达式为

(2)

式中,α为旋转角。精密星历轨道坐标转换为惯性系坐标后,运用三角函数插值法进行插值,得到惯性系坐标插值结果,再转换为地固系坐标,与已知坐标作差后进行比较。

三角函数插值多项式的形式[12]为

X′t=a0+a1sin(ωt)+a2cos(ωt)+a3sin(2ωt)+

a4cos(2ωt)+…+ancos(nωt/2)

(3)

式中,X′t为对应历元时刻t下精密星历轨道坐标X方向分量;n为三角函数对应的阶数;ω=2π/T(T为BDS卫星运行周期,其中GEO和IGSO卫星周期为23 h 56 min,MEO卫星周期为12 h 50 min);a0、a1、…、an为求得的三角函数系数。

根据已获得的星历数据,对式(3)进行展开为

(4)

对式(4)线性方程组求解,得到待求系数a0、a1、…、an。将待求系数代入式(3)中,即可得到任意时刻BDS卫星轨道在X方向的坐标分量,同理可求得BDS卫星在Y方向和Z方向的坐标分量。

1.2 广义延拓逼近法外推模型

已知一组数据(x1,t1),(x2,t2),…,(xi,ti),…,(xn,tn) ,若求取tn+1时刻xn+1的值,则令tn为最新时刻,采用外推算法求取tn+1时刻的值xn+1,现以卫星坐标在X方向分量为例,建立广义延拓外推模型[18]为

(5)

式中,n为已知卫星轨道坐标点数量;a1、a2、a3为待求系数;tn为卫星轨道坐标对应的时间点;xn为tn时刻对应的卫星轨道坐标在X方向的分量。上述模型为有约束优化模型,把上述模型展开求解,即按约束条件可得

(6)

把式(6)代入最小二乘公式可得

(7)

则按

(8)

可写成矩阵形式

(9)

其中

由式(9)得

(10)

求得待求系数a2、a3后,代入式(6)中,即可得a1,则可得外推公式为

(11)

同理可得BDS卫星在Y和Z方向轨道坐标分量的外推公式。

2 两种卫星轨道坐标外推方法精度分析

为验证两种卫星轨道坐标外推方法的精度,本文从IGS官网下载了2021年10月10日北斗卫星轨道坐标的精密星历,选取PC16(GEO卫星)、PC22(IGSO卫星)及PC36(MEO卫星)作为分析对象。历元时刻为00:00:00—24:00:00,采样时间间隔为15和5 min,选取的先验数据点的个数为13、17、21和25。以先验数据为已知数据,运用两种坐标外推方法构建数学模型,每隔5 min外推23:50:00—24:00:00时段的卫星精密星历。

假如采样间隔为15 min,先验数据点为13个,则在历元时刻为20:45:00—23:45:00的时段中,每隔15 min选取卫星精密星历数据,共选取13个作为先验数据,每隔5 min外推23:50:00—24:00:00时段的卫星精密星历,与外推点处历元对应的卫星坐标作差后进行比较,求出误差绝对值的最大值和误差中误差,并求出相应的点位中误差。本文试验运算环境为Matlab 9.8。IGS精密星历数据误差一般小于5 cm,因此两种外推算法的精度至少小于5 cm才能满足要求。

2.1 先验数据个数为13个时两种外推方法精度分析

2.1.1 GEO卫星精密星历外推精度分析

表1是先验数据为13个时,GEO卫星不同时间间隔X方向三角函数外推精度。当时间间隔为15 min时,随外推阶数的增大,X方向差值和中误差的精度不断提高,在10阶时分别为4.15和2.98 cm;当时间间隔为5 min时,X方向差值和中误差则随着外推阶数的增大而不断增大,在6阶时精度最高,分别为0.44和0.28 cm,比15 min时间间隔的最优精度高出了1个数量级。表2是先验数据为13时,GEO卫星不同时间间隔X方向广义延拓外推精度。当时间间隔为15 min时,外推精度随阶数的增大呈现先增高后降低的趋势,在第9阶精度最高;当时间间隔为5 min时,外推精度在7阶时最高,差值和中误差分别为1.23和0.77 cm,比15 min时间间隔的外推精度有了很大的提升,能够满足精度的要求。

表1 GEO卫星X方向三角函数外推精度 cm

表2 GEO卫星X方向广义延拓外推精度 cm

2.1.2 IGSO卫星精密星历外推精度分析

表3是先验数据为13个时,IGSO卫星不同时间间隔X方向三角函数外推精度。当时间间隔为15 min时,随外推阶数的增大,X方向三角函数外推的差值和中误差精度总体上呈现不断增高的趋势,在10阶时精度达到最高;当时间间隔为5 min时,X方向三角函数外推的差值和中误差随阶数的增大先减小后增大,在7阶时达到最小,与15 min时间间隔最优精度相比,精度相近。表4除了在5 min时间间隔的8阶时IGSO卫星X方向广义延拓外推中误差为4.88 cm,其余外推结果精度均较低,不能够满足卫星精密星历轨道坐标的精度要求。

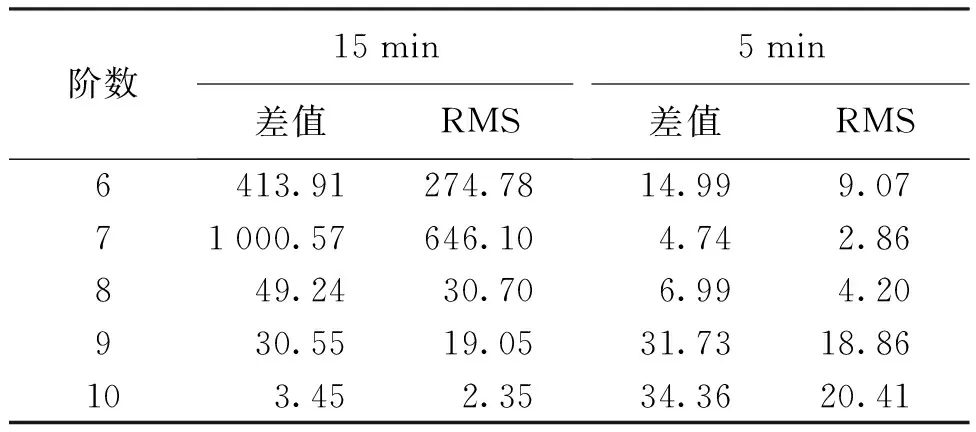
表3 IGSO卫星X方向三角函数外推精度 cm

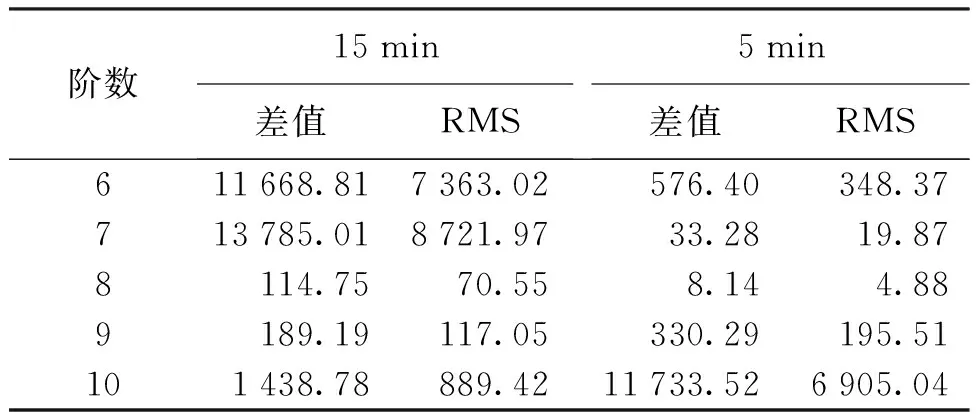
表4 IGSO卫星X方向广义延拓外推精度 cm

2.1.3 MEO卫星精密星历外推精度分析

表5是先验数据为13个时, MEO卫星X方向三角函数外推精度。当时间间隔为15 min时,随外推阶数的增大不断提高,在10阶时精度达最高;5 min时间间隔的X方向误差和中误差在7阶时精度最高,小于5 cm,符合精度要求。表6是先验数据为13时,MEO卫星不同时间间隔X方向广义延拓外推精度。在15和5 min时间间隔时,X方向广义延拓外推的差值和中误差均随阶数增大先减小后增大,但无论是15 min,还是精度更高的5 min时间间隔的外推结果,其精度均不能满足要求。

表5 MEO卫星X方向三角函数外推精度 cm

表6 MEO卫星X方向广义延拓外推精度 cm

2.2 不同先验数据个数时两种外推方法最优精度分析

2.2.1 GEO卫星精密星历外推最优精度分析

表7为 GEO卫星X方向三角函数外推精度的比较。可以看出,随着先验数据个数的增加,15 min时间间隔的差值、中误差和点位中误差精度相近,且均小于5 cm;随着先验数据时间间隔的缩短,当时间间隔为5 min时,精度有了较大的提高。先验数据为13和17个时,X方向差值和中误差精度都达到了毫米级。表8为GEO卫星X方向广义延拓外推精度的比较。可以看出,相较于三角函数外推精度,15 min时间间隔的精度较低,且都大于5 cm,不能满足精度的要求;相较于15 min时间间隔的外推精度,5 min时间间隔的外推精度达厘米级,先验数据为13个,在7阶时精度最高,差值、中误差和点位中误差分别为1.23、0.77和2.65 cm。

表7 GEO卫星X方向三角函数外推最优精度统计 cm

表8 GEO卫星X方向广义延拓外推最优精度统计 cm

2.2.2 IGSO卫星精密星历外推最优精度分析

表9为IGSO卫星X方向三角函数外推精度的统计。当时间间隔为15 min、先验数据为13和25个的最优阶时,差值和中误差的精度可以达到毫米级;当时间间隔为5 min时,随着先验数据的增加,精度越来越高,先验数据为25个时达到最优精度。表10为IGSO卫星X方向广义延拓外推最优精度的统计,只有在5 min时间间隔时,精度较高。在先验数据为25个、最优阶数为9阶时,差值、中误差和点位中误差分别为0.3、0.21和3.23 cm。

表9 IGSO卫星X方向三角函数外推最优精度统计 cm

表10 IGSO卫星X方向广义延拓外推最优精度统计 cm

2.2.3 MEO卫星精密星历外推最优精度分析

表11为MEO卫星X方向三角函数外推最优精度的结果统计。当时间间隔为15 min、先验数据为21个,最优阶为14时,差值为6.3 cm,精度最低;其余3个不同先验数据个数最优阶精度相近,且都能符合精度要求。5 min时间间隔的外推精度随着先验数据的增加而提高,在先验数据为25个时,差值、中误差和点位中误差分别为1.61、0.95和2.01 cm。表12为MEO卫星X方向广义延拓外推最优精度的结果统计。当时间间隔为15 min时,精度达到米级,不符合精度要求;随着外推时间间隔的减小,时间间隔为5 min时,精度随着先验数据个数的增加先增高后降低,在先验数据为17个时,差值和中误差的精度能达到毫米级。

表11 MEO卫星X方向三角函数外推最优精度统计 cm

表12 MEO卫星X方向广义延拓外推最优精度统计 cm

3 结 论

本文基于IGS官网发布的15和5 min时间间隔的北斗卫星精密星历轨道坐标,运用三角函数插值多项式和广义延拓逼近法数学模型,对2021年10月10日PC16、PC22和PC36 3颗北斗卫星精密星历进行了5 min时间间隔的轨道坐标外推计算和精度分析。结果表明:

(1)对不同类型北斗卫星精密星历进行轨道坐标外推,即使是同一种方法,精度也不同。 GEO卫星相较于IGSO卫星和MEO卫星,运用同一种方法进行轨道坐标外推,无论是15 min还是5 min时间间隔,精度都相对更高。

(2)两种外推方法在对同一颗北斗卫星进行轨道坐标外推时,三角函数插值多项式相比于广义延拓逼近法,在15 min时间间隔时,三角函数外推精度比广义延拓逼近法高1～2个数量级;在5 min时间间隔时,只要选择合适的阶数,两种外推方法精度都能达到厘米甚至毫米级,但是三角函数相较于广义延拓逼近法精度更高。

(3)两种外推方法对不同类型北斗卫星精密轨道坐标进行外推计算时,5 min时间间隔的计算精度相较于15 min时间间隔,精度更高,广义延拓逼近法5 min时间间隔的计算精度相较于15 min时间间隔,精度能高出1～2个数量级。因此,可以优先选用5 min时间间隔的卫星精密星历进行轨道坐标外推计算。