改进的深度残差收缩网络轴承故障诊断方法

唐世钰, 童靳于,2, 郑近德, 潘海洋, 伍 毅

(1. 安徽工业大学 机械工程学院,安徽 马鞍山 243032;2. 安徽省智能破拆装备工程实验室,安徽 马鞍山 243032)

滚动轴承作为机械传动系统的关键零部件,在复杂多变的工况下长期运行后,不可避免地会出现各种故障,可能影响整机的性能,导致严重的安全事故。因此,准确、自动地诊断滚动轴承中可能发生的不同故障具有重要意义[1-2]。

随着计算技术的发展,支持向量机(support vector machine, SVM)[3]、K近邻算法[4]等传统的机器学习方法,已被应用于故障诊断领域。这些机器学习方法往往需要结合人工经验选取特征,计算耗时且准确率不高。

2006年,Hinton等[5]首次提出了深度学习的概念。与传统的机器学习不同,深度学习可以实现端到端的学习,在进行学习前不需要进行特征提取等操作,通过加深网络结构即可实现从原始数据中自动提取特征的目的[6]。其中,自动编码器(auto-encoder, AE)[7]、卷积神经网络(convolutional neural network, CNN)[8]、深度信念网络(deep belief network, DBN)[9]等已被广泛应用于故障诊断中。例如,文献[10]将卷积DBN应用于电力机车轴承的故障诊断。文献[11]采用一维CNN从原始信号中学习特征,用于电机的故障诊断。文献[12]设计了一种基于稀疏AE的故障诊断模型用于识别感应电动机的故障类别。

在深度学习中,一般通过增加网络的层数来提高模型的性能[13]。然而,网络层数的增加会阻碍梯度的流动,加大参数优化的难度,进而导致故障诊断准确率降低。He等[14]提出了深度残差网络(deep residual network, ResNet),其核心是使用快捷连接避免了梯度爆炸和消失,缓解了参数优化的困难。近年来,ResNet及其变体被应用到故障诊断领域。例如,Zhao等[15]使用ResNet融合多组小波包系数进行故障诊断。Zhang等[16]提出了一种基于混合注意力机制的ResNet方法,其在振动信号的时频特征提取、频带信息增强和识别精度提高等方面具有优异的性能。ZHAO等[17]提出了一种深度残差收缩网络(deep residual shrinkage network, DRSN),DRSN将软阈值作为收缩层引入ResNet的残差单元(residual building unit, RBU)中,可以过滤掉信号中与噪声相关的特征。

在DRSN方法中,由于软阈值的局限性,使用软阈值降噪的同时会过滤信号中与故障相关的特征,从而引起信号失真,导致故障诊断精度降低。为了解决上述问题,本文提出了一种改进的深度残差收缩网络(improved deep residual shrinkage network, IDRSN),并将其应用于滚动轴承故障诊断中。首先,引入了一种改进的半软阈值函数(improved semi-soft threshold function, ISSTF),用于消除软阈值函数在降噪过程中引起的信号失真。其次,设计了半软阈值模块(semi-soft threshold block, SSTB)和自适应斜率模块(adaptive slope block, ASB)自适应地设置最优阈值,避免人工设定阈值的繁琐和不合理。最后,将IDRSN应用于不同工况的滚动轴承故障诊断中。研究结果表明,与现有方法相比,所提方法不仅能够有效诊断故障,而且诊断精度更高。

1 本文所提方法

本文提出了一种改进的深度残差收缩网络IDRSN,并将其应用于滚动轴承的故障诊断中。

1.1 改进的半软阈值函数

在信号处理领域,软阈值处理经常被作为信号去噪的关键步骤[18]。一般情况下,传统的去噪方法需要设计一个滤波器,将原始信号中有用的信息转换为正或负的特征,将噪声信息转换为接近零的特征。但是,在这个过程中应该将哪些信息判定为有用信息,哪些信息判定为噪声信息,这需要大量的专家经验。DRSN首次将深度学习与软阈值处理相结合,与ResNet的RBU层不同,DRSN中设计了残差收缩单元(residual shrinkage building unit, RSBU)。RSBU层使用软阈值化去除与噪声相关的特征,将软阈值作为一个非线性变换层插入到RBU层中,并利用注意力机制自适应地学习阈值。

软阈值函数可以表示为

(1)

式中:x为输入;y为输出;τ为阈值。

从式(1)可以看出,经过软阈值函数处理,数据仍具有良好的连续性,但当|x|≥τ时,y和x始终存在恒定偏差,这会造成一些有效信息的丢失,导致信号一定程度上的失真,进而降低诊断的准确性。

为了缓解DRSN中软阈值函数的缺点,本文将一种半软阈值函数ISSTF[19]引入DRSN中,ISSTF定义如下

(2)

软阈值化和半软阈值化过程如图1所示。从式(2)和图1可以看出,ISSTF首先保留了软阈值函数的连续性,当|x|<τ时,ISSTF将近零的特征转换为0,这与软阈值函数相同。更重要的是,当|x|≥τ时,输入和输出呈现非线性关系,且随着|x|增大,输入和输出的偏差逐渐减小,消除了软阈值函数存在的恒定偏差问题,最大程度地保留了有效特征。

图1 不同阈值函数对比图Fig.1 Comparison chart of different threshold functions

1.2 改进的深度残差收缩网络

本文提出了一种改进的深度残差收缩网络IDRSN。一方面,在降低信号中噪声的同时更好地保留了有效信号;另一方面,实现了网络自适应关注重要特征的目的。

1.2.1 网络结构

IDRSN由输入层、卷积层(convolutional layer, Conv)、多个改进的残差收缩单元(improved residual shrinkage building unit, IRSBU)层和全连接层(fully connected layer, FC)组成,其网络结构如图2所示。

图2 IDRSN的网络结构Fig.2 Network structure of IDRSN

1.2.2 改进的深度残差收缩单元(IRSBU)

在DRSN中,由于RSBU层的输入和输出存在恒定偏差,导致有效特征信息被过滤,进而造成故障诊断精度降低。本文针对DRSN中RSBU层的不足,设计了一种改进的残差收缩单元IRSBU,如图3所示。图3中:C和W为特征图的通道数和宽度。

图3 IRSBU结构Fig.3 Structure of IRSBU

IRSBU单元使用改进的半软阈值ISSTF代替RSBU单元中的软阈值函数,将改进的半软阈值作为一个非线性变换层插入到RBU中,去除与噪声相关的特征,同时更好地保留有效信号。

此外,为了自适应设置最优阈值,避免人工设定阈值的繁琐和不合理,IRSBU单元设计了半软阈值模块SSTB和自适应斜率模块ASB。其中,SSTB模块可以使阈值保持在一个合理的范围内,ASB模块可以更进一步修正半软阈值。

SSTB与RSBU中所设计的阈值模块结构基本相同。首先对特征x的绝对值使用GAP(global average pooling),得到一个一维向量;再将一维向量传递到两层FC网络中,得到一个尺度参数,其中第二层FC神经元个数等于输入特征图的通道数;然后在两层FC网络的末端应用一个Sigmoid函数,从而使尺度参数被缩放到(0,1)内。尺度参数可以表示为

(3)

式中:zc为第c层神经元的特征;σc为第c层的尺度参数。

那么,半软阈值τc定义为

(4)

式中,i,j,c分别为特征图X的宽度、高度和通道。学习到的半软阈值τc为正,且保持在一个合理的范围内。

ASB模块利用注意力机制自动推断出最合适的斜率。ASB模块的输出为

(5)

式中:a为自适应斜率因子;ac为第c层神经元的特征。

然后,利用ASB模块的输出进一步修正半软阈值,表示如下

(6)

从上述过程可以看出,与RSBU相比,IRSBU能有效地去除与噪声相关的特征,同时能更有效地保留有效信号,从而保留更多特征敏感信息。

1.4 基于IDRSN的滚动轴承故障诊断流程

基于IDRSN的故障诊断流程如图4所示,具体步骤如下:

图4 基于IDRSN的故障诊断流程图Fig.4 Flow chart of fault diagnosis based on IDRSN

步骤1采集原始时域振动信号。

步骤2按照一定比例,将原始时域信号随机划分为训练集和测试集。

步骤3使用训练集训练IDRSN,设置训练参数,使用反向传播算法对网络参数进行微调,直到误差收敛。

步骤4将测试集输入到IDRSN模型中,获得测试精度。

2 试验验证与结果分析

本章采用两个不同试验台数据集验证所提方法的可行性和优越性,分别为凯斯西储大学(Case Western Reserve University, CWRU)滚动轴承数据集[20]和安徽工业大学自制数据集。其中,试验一为恒定转速数据集,试验二为变转速数据集。

2.1 滚动轴承信号采集

2.1.1 试验一

试验一为CWRU的滚动轴承实验,试验台如图5所示。试验的轴承型号为SKF6205-2RSJEM,通过电火花加工技术设置单点故障。选取负载为745.7 W,采样频率为12 kHz转速为1 772 r/min工况下的滚动轴承振动信号,包含10种健康状态:故障直径为0.177 8 mm,0.355 6 m,0.533 4 mm的内圈故障(分别标记为IR1,IR2,IR3),故障直径为0.177 8 mm,0.355 6 mm, 0.533 4 mm的外圈故障(分别标记为OR1,OR2,OR3),故障直径为0.177 8mm,0.355 6 mm,0.533 4 mm的滚动体故障(分别标记为BA1,BA2,BA3)和正常状态(标记为NO)。不同健康状态下的轴承振动时域信号如图6所示。

图5 凯斯西储大学轴承试验平台Fig.5 Bearing test platform of CWRU

图6 试验一滚动轴承振动时域信号Fig.6 Time domain signal of rolling bearing vibration of test 1

2.1.2 试验二

试验二采用自制滚动轴承故障模拟试验台,由变频电机、加载装置和待测滚动轴承等零部件组成,其结构如图7所示。待测滚动轴承型号为SKF6205,采用线切割技术在内、外圈、滚动体和保持架上加工出不同程度的故障,故障类型如图8所示。

图7 轴承故障模拟试验装置Fig.7 Bearing failure simulation test device

图8 不同健康状态的滚动轴承Fig.8 Rolling bearings in different health conditions

采用振动加速度传感器采集负载为1 kN,转速从100 r/min经过20s加速至1 500 r/min工况下的滚动轴承振动信号,采样频率设置为10 kHz,包含10种健康状态:故障深度为0.3 mm,0.5 mm的内圈故障(分别标记为IR1,IR2);故障深度为0.3 mm,0.5 mm的外圈故障(分别标记为OR1,OR2);滚动体点蚀(标记为BA);滚动体点蚀+外圈0.3 mm,内外圈0.3 mm和内外圈点蚀的3类复合故障(分别标记为C1,C2,C3);保持架断裂(标记为BCJ)和正常状态(标记为NO)。不同健康状态下的轴承振动时域信号如图9所示。

图9 试验二滚动轴承振动时域信号Fig.9 Time domain signal of rolling bearing vibration of test 2

2.2 数据集描述

分别选取试验一和试验二的滚动轴承振动信号,在同一故障类型下,每类故障随机取100个样本,每个样本包含1 024个点[21],试验一和试验二各制作了1 000个样本。从中随机抽取80%样本用于训练,20%样本用于测试。试验一和试验二的轴承数据集分别如表1和表2所示。

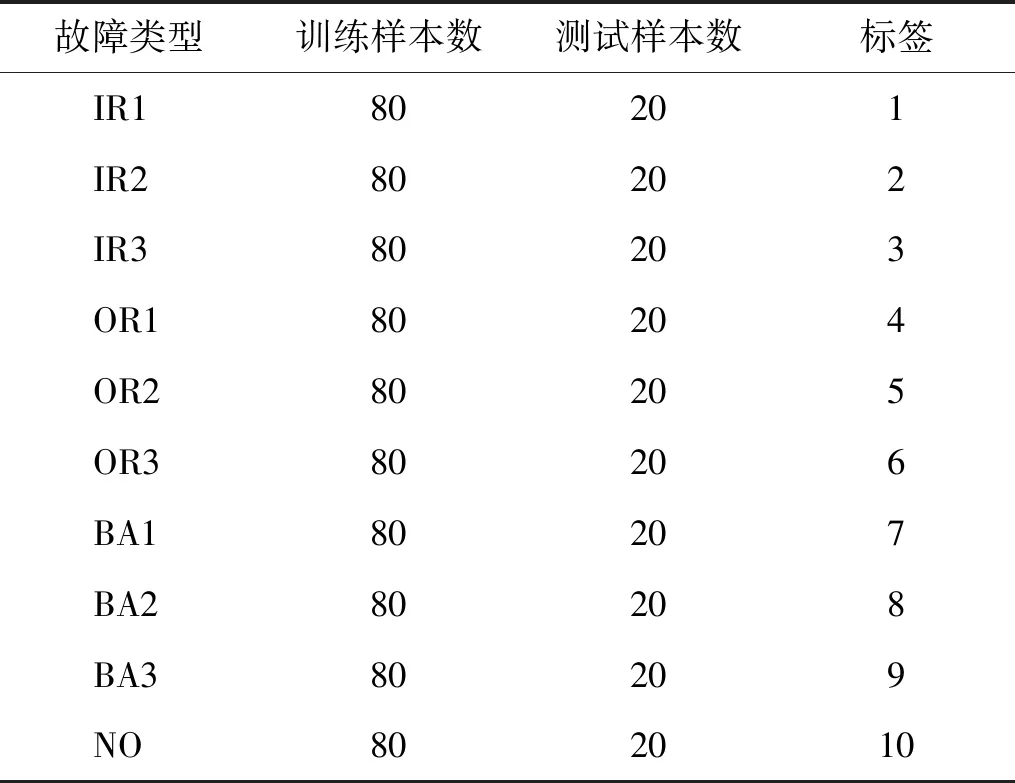
表1 试验一轴承数据集

表2 试验二轴承数据集

2.3 模型参数设置

IDRSN模型包括1个Conv层、12个IRSBU层、1个GAP层和1个FC层,网络参数如表3所示。在IDRSN训练过程中,参数设置如下:L2正则化系数设置为1×10-4,批大小为16,采用Adam优化算法,迭代次数为100次。

表3 IDRSN的网络参数

2.4 消融试验

本节采用消融试验验证IDRSN中所提模块的可行性。试验设置了两个控制模块:ISSTF和ASB,共设置了4种模型,不同模型的控制模块如表4所示。其中,模型A为IDRSN,模型B是在IDRSN的基础上移除ASB,模型C是在DRSN的基础上加上ASB,模型D是DRSN。

表4 不同模型的变量设置

2.4.1 消融试验结果

为了减少随机因素对试验结果的影响,每个模型做10次试验,取10次试验的平均值和标准差作为评估标准。试验一和试验二的10次消融试验结果分别如图10和图11所示,10次试验的平均准确率和标准差如表5所示。

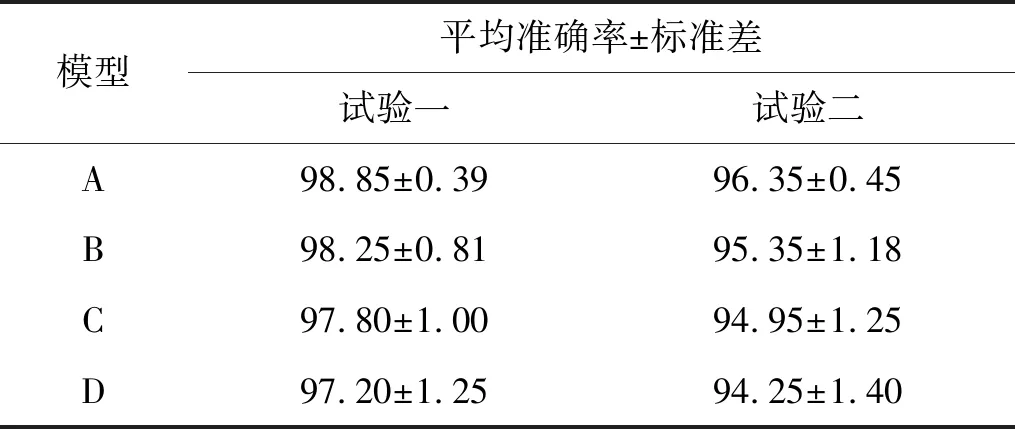
表5 对比模型的平均准确率和标准差

图10 试验一消融试验结果Fig.10 Results of ablation tests of test 1

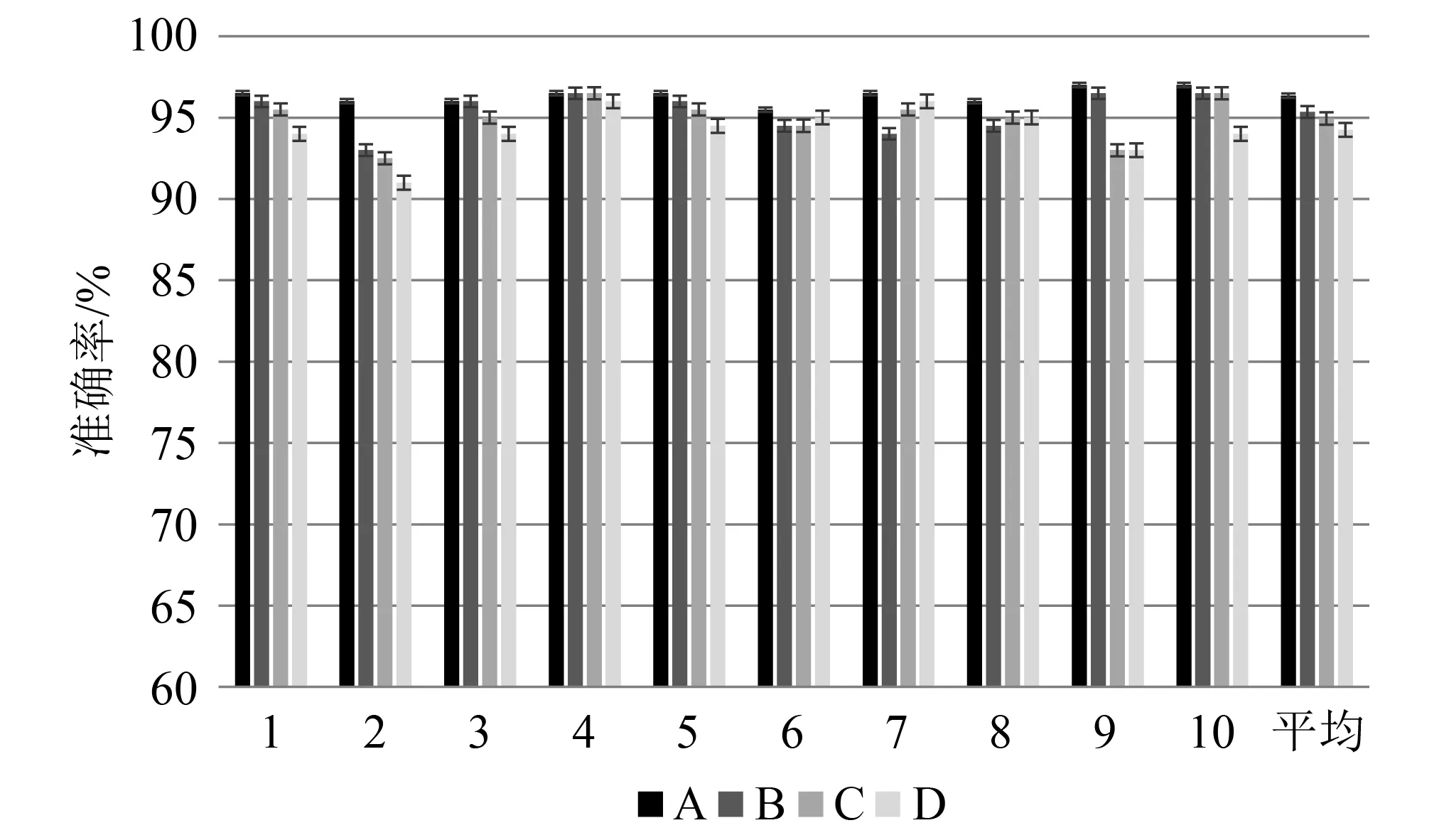
图11 试验二消融试验结果Fig.11 Results of ablation tests of test 2

2.4.2 消融试验结果分析

从图10、图11和表5中可以看出,相较于模型D,模型B在两个试验中的平均准确率分别提高了1.05%和1.10%,且标准差减小了35.20%和15.71%,说明在IDRSN中,ISSTF能够提高模型的诊断效果且使模型更稳定。相较于模型D,模型C在两个试验中的平均准确率分别提高了0.60%和0.70%,且标准差减小了20.00%和10.71%,说明ASB也能够在一定程度上提高模型的诊断效果。上述对比结果说明,ISSTF模块和ASB模块均能提高模型的诊断性能和稳定性。

2.5 对比试验

本节采用对比试验验证所提方法的优越性。对比模型为IDRSN,DRSN,ResNet,CNN和SVM。为了公平对比,5种模型均使用原始数据作为输入,且DRSN,ResNet,CNN与IDRSN模型的网络结构参数相同(见表3),SVM的核函数采用RBF函数,惩罚因子设置为1,核函数参数设置为0.125。

2.5.1 对比试验结果

为了减少随机因素对试验结果的影响,每个模型做10次试验,取10次试验的平均值和标准差作为评估标准。试验一和试验二的10次对比试验结果分别如图12和图13所示,10次试验的平均准确率和标准差如表6所示。

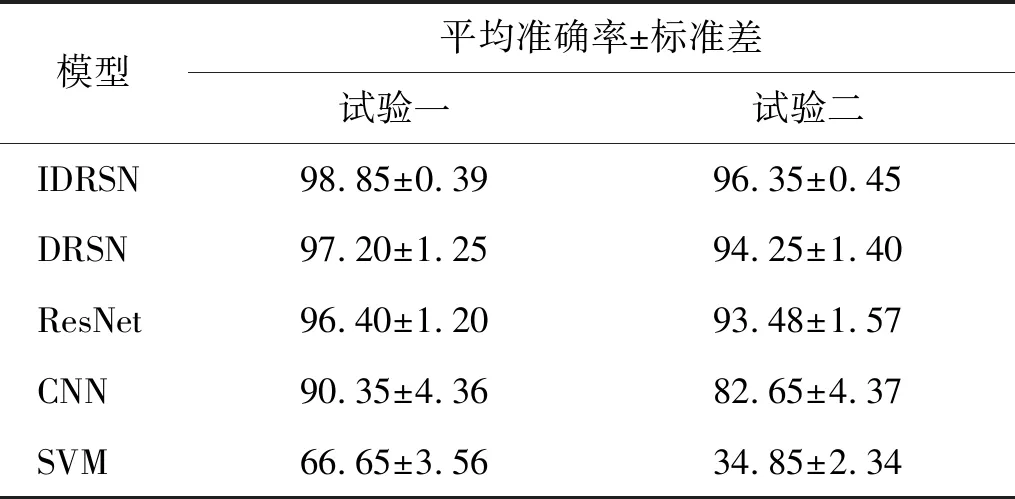
表6 对比模型的平均准确率和标准差

图12 试验一对比试验结果Fig.12 Comparative test results of test 1

图13 试验二对比试验结果Fig.13 Comparative test results of test 2

2.5.2 对比试验结果分析

从图12、图13和表6可以看出,作为传统的机器学习算法,SVM平均准确率远低于深度学习方法,说明传统机器学习方法无法充分提取故障敏感特征。在几种深度学习方法中,传统CNN模型表现最差,主要原因是其他几种模型采用的快捷连接方式极大地促进了梯度流动,减轻了参数优化的难度,从而使诊断性能更加稳定。

在试验一中,与DRSN和ResNet相比,IDRSN的平均准确率分别提高了1.65%和2.45%,且标准差减小了68.80%和67.50%;在试验二中,与DRSN和ResNet相比,IDRSN的平均准确率分别提高了2.10%和2.87%,且标准差减小了67.86%和71.34%。由此说明,IDRSN模型最大程度地减少了信号的失真,保留了更多的有效信号,具有较高的分类准确率和良好的稳定性。

对比试验一和试验二的结果可以发现,5种模型的平均准确率和稳定性都有不同程度的下降。这是因为试验二使用了变转速数据集,转速的变化导致振动信号的特征差异变大,从而影响故障诊断精度。但在所有模型中IDRSN平均准确率下降最少,体现了IDRSN较好的鲁棒性。

2.6 可视化分析

为了更直观地分析IDRSN的故障诊断效果,利用t-分布领域嵌入[22]算法可视化二维空间中原始信号和IDRSN中Softmax层的高级特征。试验一和试验二的特征散点图如图14和图15所示。从图14、图15可以看出,两个试验10类原始信号随机分散在二维平面上,相互重叠,难以区分。而IDRSN在Softmax层提取到的特征聚类效果很好,轻易就能分辨,证明了IDRSN在恒定转速和变转速工况下均具有较高的识别精度。

图14 试验一特征可视化Fig.14 Feature visualization of test 1

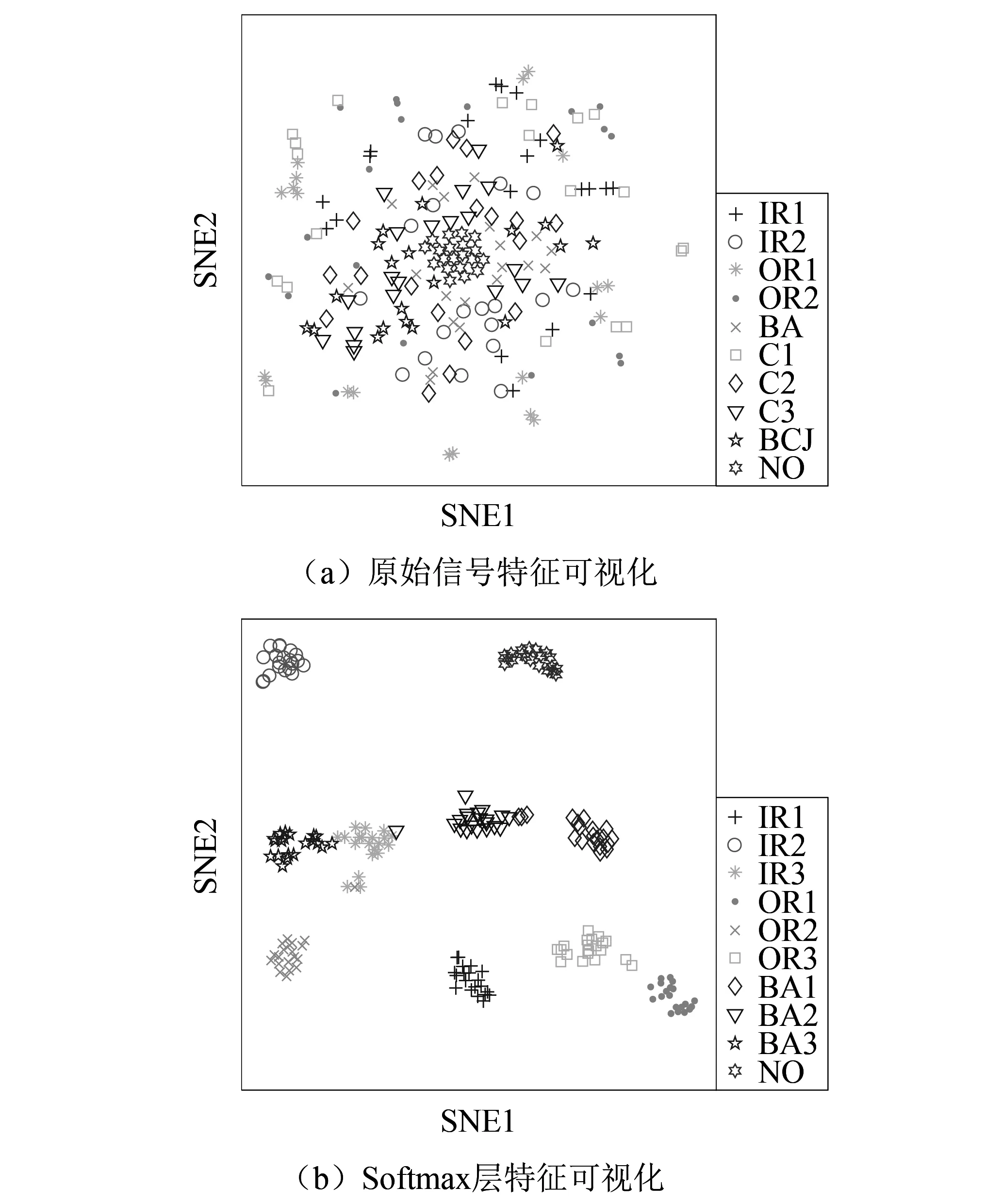
图15 试验二特征可视化Fig.15 Feature visualization of test 2

3 结 论

本文提出了一种改进的深度残差收缩网络,并将其应用于滚动轴承诊断中,主要结论如下:

(1)本文使用的ISSTF阈值函数效果优于DRSN中的软阈值函数,能够在去除噪声的同时更有效地保留故障敏感特征,增强了DRSN的性能。

(2)本文设计的SSTB和ASB模块,可以自适应地设置阈值,进一步提升了DRSN的性能。

(3)通过两种不同类型的滚动轴承试验验证了IDRSN在诊断准确率和稳定性方面更具优势,特别是针对变转速工况下的故障诊断更为有效。

虽然所提方法提高了滚动轴承的故障诊断性能,但半软阈值函数的结构会增加模型计算的时间。因此,下一步工作将致力于模型优化和降低模型的复杂性。