渗流作用下不同结构土质边坡稳定性模拟
吴星辉,钟 辉,张淑坤,王 帅,姜 鹏,王昊昊
(1.枣庄学院 城市与建筑工程学院,山东 枣庄 277160;2.山东能源集团 赵官能源有限责任公司,山东 齐河 251113)
0 引言
随着我国水利事业的发展,水力发电逐渐成为城市供电方式之一。实现水力发电需要建造堤坝用来蓄水,而堤坝在长期水力压力作用下有可能发生溃坝。如果堤坝发生溃坝,后果可能是毁灭性的,甚至是致命的。用于水力发电的堤坝造价昂贵,建造难度也很大,但是强降雨和洪水会导致坝体后面的蓄水迅速上涨,静水压力逐渐增大。当坝体抵挡不住静水压力发生渗流时,坝体最终产生破裂。坝体部分坍塌,对人类生命和财产造成威胁。
堤坝结构的完整性是溃坝的关键因素,有学者提出,应在堤坝建造之前分析堤坝的稳定性和可靠性。堤坝的建造一般是以边坡的形式存在,对边坡稳定性分析可用于预测各种载荷和环境条件引起的堤坝土壤的沉降、变形和滑移。随着计算机技术和数值模拟软件的迅猛发展,数值模拟研究成为边坡问题分析的主要方法[1-2]。针对边坡稳定性分析,常采用强度理论与数值分析相结合的方法,对边坡受力状态进行分析,得到边坡受力情况判断边坡变形程度[3-5]。宋云连等[6]采用蒙特卡洛法与有限元数值分析相结合的方法,讨论边坡滑裂带在加固前后稳定性指标,提供了一种边坡稳定性分析方法。安全系数是评价边坡稳定性的有效指标,刘彦等[7]采用有限元强度折减法计算了边坡安全系数,计算结果与刚体极限平衡法相同。张冬岩等[8]通过有限元强度折减法与莫尔库伦强度准则结合计算了边坡安全系数,同时分析了边坡破坏模式,为边坡角的确定提供了依据。尽管基于强度理论的边坡稳定性分析已取得了诸多研究成果,但由于实际工程中坝体受静水压力边界影响,坝体内部渗流场复杂,坝体在渗流作用下抗剪强度降低,对坝体稳定性产生显著影响[9-10]。在渗流-应力作用下利用剪切强度折减法对不同坝体设计的边坡稳定性分析尚未开展。
本文通过对边坡渗流-应力耦合场模拟分析,得到渗流场的压力分布规律。考虑坝体土壤渗流软化作用,采用剪切强度折减法对不同结构形式的土质边坡稳定性进行分析,计算得到不同结构形式的土质边坡安全系数。结合莫尔-昆仑准则计算了边坡等效塑性应变,预测坡体失稳滑移面,总结了渗流场对不同结构土质边坡稳定性的影响规律。
1 剪切强度折减法原理
强度折减法是边坡稳定性分析中最常见的方法之一,是将边坡基质抗剪参数与边坡安全系数建立的函数关系。随着渗流作用对坡体的影响增加,边坡基质剪切强度会降低,在重力和静水压力共同作用下导致边坡失稳。莫尔-库仑模型的材料属性根据安全系数F进行参数演化,通过反复迭代计算直到模型不能够收敛,表明边坡发生失稳。在迭代计算过程中,模型不能收敛时的安全系数为边坡最小安全系数Fs,同时可以得到有效塑性应变和滑移面。计算得到的Fs越大,边坡越稳定[11],莫尔-库仑屈服函数及相关塑性势为:
(1)
α=sinφ/3,
(2)
k=ccosφ,
(3)
式中:m为材料常数,I1、J2分别为莫尔-库伦应力张量的第一、第二不变量,φ为土壤内摩擦角,c为土壤内聚力。
剪切强度折减法表达式为:
ci=c/Fi,
(4)
(5)
τi=ci+σtanφi,
(6)
式中:Fi为边坡强度折减系数,ci为对应强度折减系数Fi的内聚力,φi为对应强度折减系数Fi的内摩擦角,φu和φs分别为非饱和土与饱和土的内摩擦角,p为达西定律给出的孔隙压力,τi为对应强度折减系数Fi的抗剪强度。若边坡失稳时,则Fi为边坡安全系数。
2 有限元模型建立
本文以土石坝为研究对象,土石坝是由左右对称的边坡组成,图1为堤坝剖面图。库水位高度为10 m,可能渗流高度为4 m。土石坝一旦建造完成,临靠水侧的边坡很难再次进行改造,所以临水侧的边坡结构尤为重要,临水侧边坡角为α。
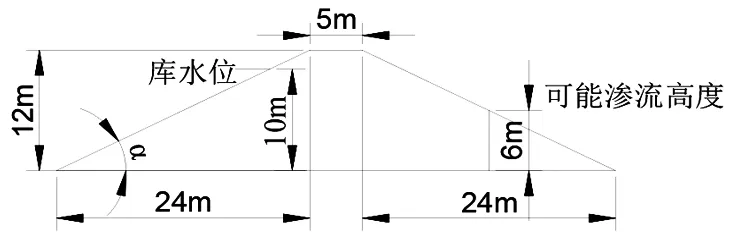
图1 土石坝示意图
2.1 几何模型建立
依据土石坝示意图尺寸,借助于多场耦合仿真软件Comsol Multiphysics建立有限元模型。模型采用物理场控制网格的序列类型,单元大小选择超细化,如图2所示。在库水位和可能的渗水水位处添加点,分割水坝的两侧边。在大坝下游和上游侧的水下部分添加压力水头。土壤中的孔隙压力通过达西定律建模,而堤坝的弹塑性分析采用莫尔-库仑准则。
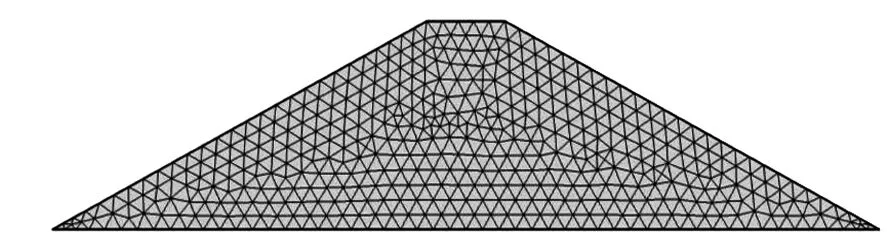
图2 土石坝有限元模型网格划分
2.2 模型参数选取
有限元模型材料分为土壤和水,模型区域材料为土壤,对于水材料,保留域选择为空。土壤和水的物理力学参数如表1所示,土壤根据内部孔隙压力分为饱和区域和非饱和区域分别参与土体内摩擦角的计算。

表1 土石坝物理力学参数
2.3 研究步设置
为了说明孔隙压力和重力载荷对堤坝稳定性的影响,本研究建立3个稳态研究步。研究步一,只计算达西定律以获得孔隙压力分布图;研究步二,用静水压力和重力载荷模拟堤坝受力状态;研究步三,通过添加预应力和预应变,将研究步一产生的孔隙压力和研究步二重力载荷产生的预应力考虑在内。研究步三增加了莫尔-库仑准则,研究重力和可变孔隙压力共同作用下的土壤弹塑性破坏。
饱和、非饱和土的内摩擦角不同,因此使用基于孔隙压力的组合。由于孔隙被认为是相互连接的并且处于恒定大气压下,因此在非饱和土区域不施加外部应力。
3 边坡稳定性分析结果
3.1 渗流影响范围
通过分析研究步一结果中的压力水头,探讨土壤受渗流影响范围,边坡的压力水头计算结果如图3所示。在浸没壁上,压力水头由0 m到10 m;而在渗流面上为0 m。正压力水头表示正孔隙压力,表明这部分土壤为饱和土,而非饱和土用零压力水头表示。图3中的零压力水头线是表示的是饱和土与非饱和土潜水面交界位置。
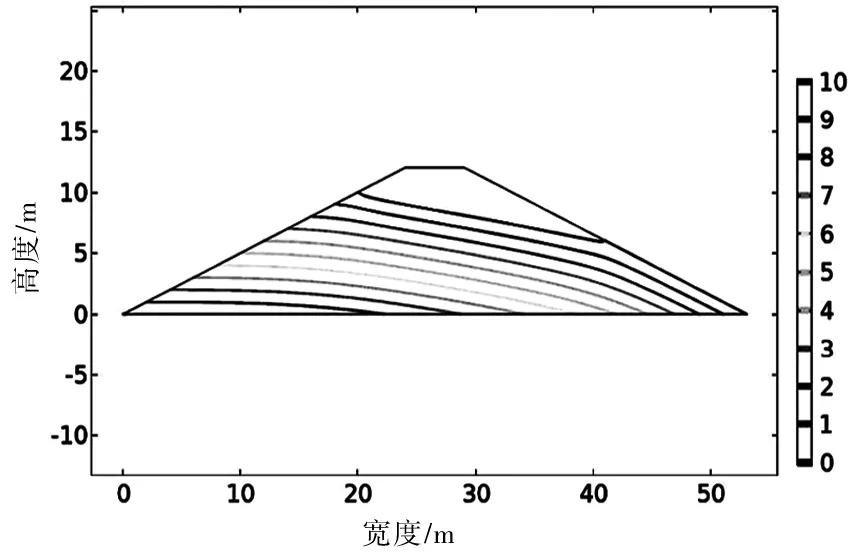
图3 坡体受渗流作用影响范围
3.2 安全系数
土石坝受渗流作用,土壤内摩擦角和内聚力不断发生变化,从而对土体强度造成影响。在模型计算过程中,引入剪切强度折减法对岩土体强度指标(Fi)不断进行迭代[12-13],得到土壤内摩擦角和内聚力代入有限元程序中,判断坡体失稳情况。本研究以模型计算不收敛作为坡体发生破坏的有效判据,边坡失稳的Fi值即为此时所得安全系数。
在模型计算过程中,将Fi从1开始,每个计算步增加0.005,当Fi值迭代超过1.915时,模型弹塑性分析不收敛。因此,由于塑性应变增加以及随后的剪切强度降低而导致边坡失稳的安全系数为1.915。考虑到渗流作用对边坡剪切强度的影响,即使边坡安全系数大于1时也有发生失稳的可能性,坡体失稳会导致位移迅速增加。图4为边坡最大位移值与Fi的关系,从图4中可知边坡最大位移在Fi为1.915开始显著增加,这表明边坡开始失稳。
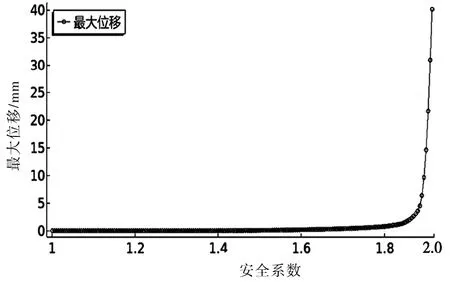
图4 坡体最大位移随Fi的变化曲线
3.3 坡体滑移面
土石坝由于渗流作用产生失稳,失稳形式以坡体滑移为主[14-15]。若能准确判断坡体滑移面的位置,可以采取有效的边坡治理措施。本研究采用失稳前的等效塑性应变显示坡体失稳模式,这表明了边坡破坏机理是土壤的塑性变形。边坡滑移面计算结果如图5所示,箭头表示土颗粒的滑移方向。由于模型下边界为固定约束,因此模型右下角土体不会出现滑移。通过边坡土体滑移现象的预测分析,可以得知边坡产生失稳时的土方量以及如何有效预防滑移的土壤对土石坝下游造成的损伤。
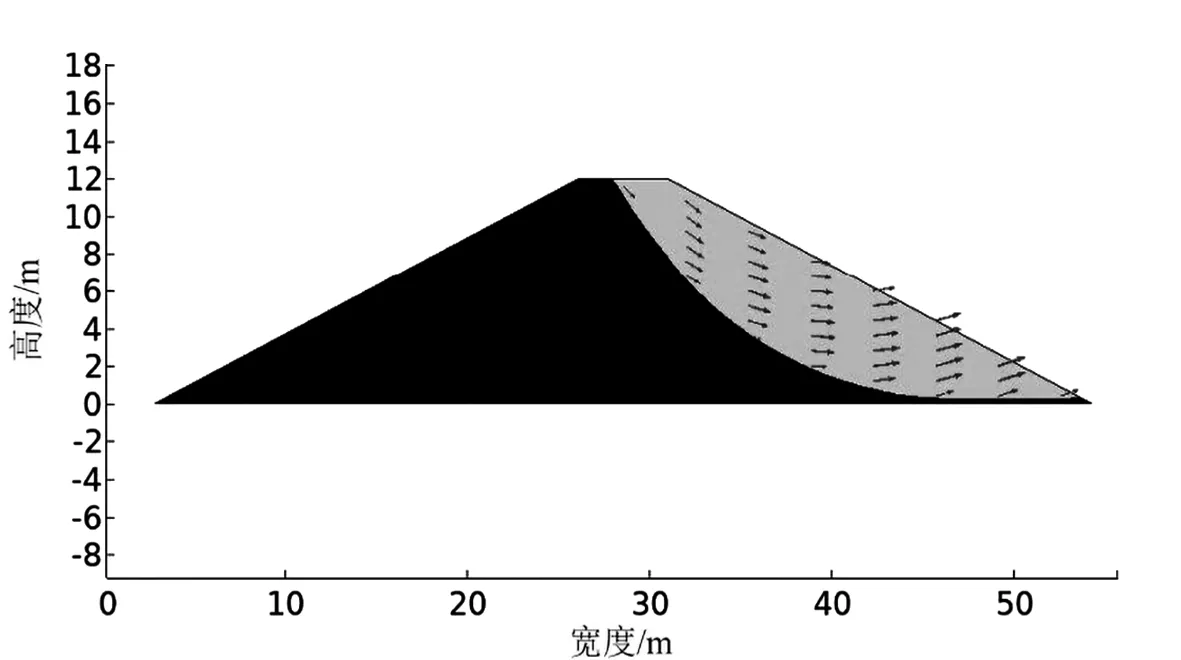
图5 边坡失稳滑移面预测
3.4 坡体位移
为了对边坡采取有效治理措施,需要分析边坡失稳时坡面整体的位移场情况。本研究借助拉伸数据集,得到了模型位移场的三维可视化效果,如图6所示。结果表明:坡体受渗流和重力荷载共同作用下,发生位移最大的区域位于坡角,最大位移可达40 mm。为了减小坡体滑移造成的损伤,建议采用压坡角和构筑挡土墙的方式减小坡角的位移。另外,对堤坝进行二维分析是用平面应变近似预测堤坝土体不稳定性的有效方法,借助后处理工具可以实现三维可视化,这种方法可避免在三维中求解较大的数值问题。
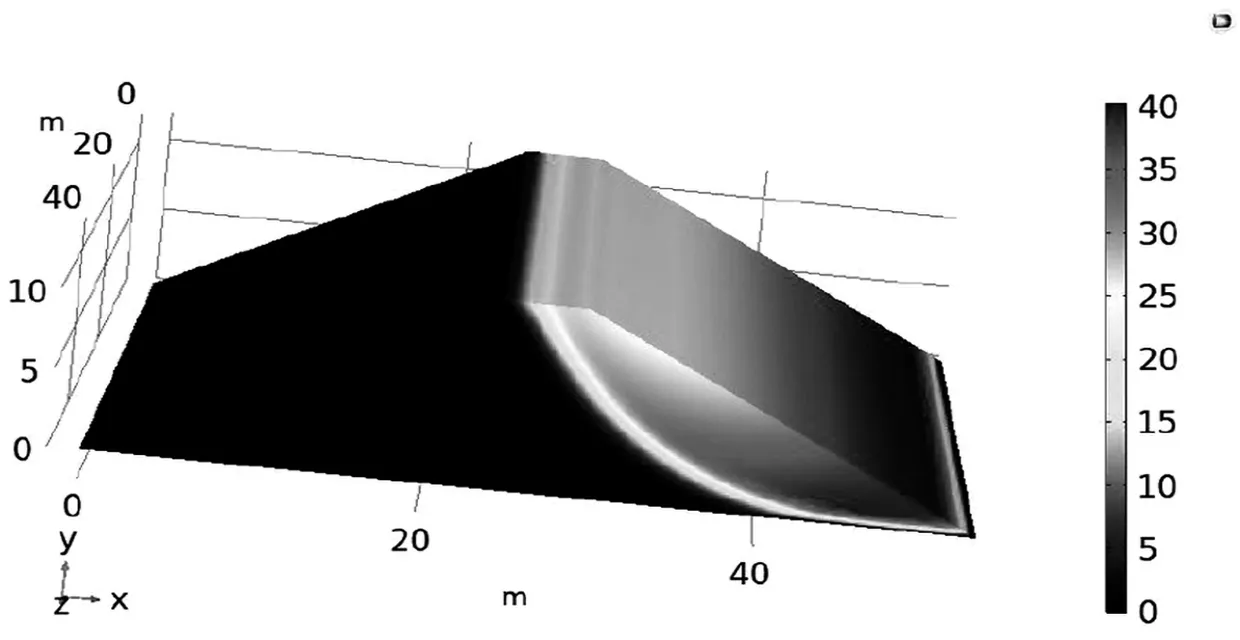
图6 边坡坡面整体位移场分布
4 不同坝体结构对边坡失稳模式影响
通过分析可知,渗流作用可以降低边坡的抗剪切强度,即使安全系数大于1时也有失稳的可能。为了有效减小渗流对边坡稳定性的影响,可以通过改变坝体结构增加边坡安全系数的方法提高边坡稳定性。本研究主要讨论临水侧边坡角α与非临水侧边坡角β的关系对边坡失稳模式的影响。由实际工程可知,边坡角α的取值范围为0°~90°,本文将边坡角α分为四类:第一类为α<β,如图7(a)所示;第二类为α=β,如图7(b)所示;第三类为α>β,如图7(c)所示;第四类为α=90°,如图7(d)所示。
基于剪切强度折减法将四种坝体结构代入有限元程序中进行计算,得到安全系数结果如表2所示。当边坡角β保持不变,边坡角α不断增加时,边坡的安全系数不断减小,边坡角α=90°时,边坡安全系数最小;边坡坡面的最大位移先不断增大而后减小。

表2 不同坝体结构安全系数及最大位移量
此外,边坡坡面的最大位移也是一个关键指标,根据计算结果发现,最大位移在边坡角α逐渐增加时先增大后减小的趋势。图8展示了在渗流和重力荷载作用下,不同坝体结构可能发生滑移现象的情况。
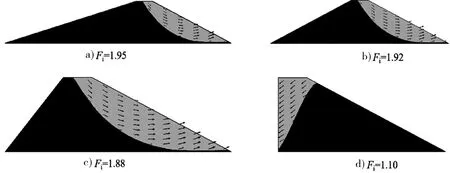
图8 不同坝体结构滑移面
由图8可知,边坡角α与边坡角β的关系对边坡滑移面有显著的影响。随着边坡角α的增加,边坡的滑移现象越明显,相应的最大位移也逐渐增加。然而,当边坡角α增加到一定值时,坝体左右边坡抗滑力与滑动力之间的关系发生变化,渗流作用更多发生在临水侧坡体上,导致边坡的滑移方向发生转变,影响最大位移。在建造临水侧坡体时,应合理设计边坡角,以防止坡体向临水侧滑移。综上所述,边坡角α对于坡体稳定性和位移特性具有重要的影响。
5 结论
本研究考虑到渗流作用对土石坝剪切强度的影响,基于剪切强度折减法对土石坝模型进行有限元数值计算,讨论不同坝体结构对边坡稳定性的影响,得到以下结论。
(1)水体的渗流作用对边坡稳定性产生显著影响,临水侧的土壤孔隙压力导致土体形成饱和状态,零压力水头将土石坝分为饱和、非饱和土体。
(2)渗流作用主要影响土壤的内摩擦角和内聚力,剪切强度折减法能够有效反映渗流作用对边坡剪切强度的影响,并且准确计算边坡安全系数,预测坡体滑移面,得到坡体的整体位移场。
(3)在渗流和重力荷载作用下,坝体结构可以影响边坡的稳定性,尤其是临水侧边坡角α与非临水侧边坡角β的关系。边坡角α比边坡角β越小,边坡越稳定。

