大型音乐节活动中人员不安全行为传播的干预研究
孙世梅,祁 兵,唐彩萍
(1.吉林建筑大学应急科学与工程学院,吉林 长春 130118;2.吉林建筑大学事故预防科学研究院,吉林 长春 130118)
近年来,国内外大型音乐节活动蓬勃发展,然而大型音乐节具有人数密集、空间开放、多元的特点,加上表演场地的观众情绪高涨,以及现场充斥着死墙、人浪、pogo、 mosh等带有危险性质的团体行为,极容易出现拥挤踩踏等突发事件,造成大量的人员伤亡。例如,2021年11月5日,美国著名音乐节“Astroworld Festival”上,当Travis Scott登场时,现场约5万名群众开始向舞台方向推挤,造成8人被踩死,上百人受伤。根据 Turris等[1]的统计数据显示,1999年至2017年间,世界各地举办的923场大型露天音乐节共造成492人死亡,上千人受伤。已有研究表明,人的不安全行为是引发大型音乐节活动拥挤踩踏事故发生的主要原因[2-4]。因此,从人的不安全行为入手,针对安全培训条件下人员不安全行为的传播规律展开研究,对预防大型音乐节事故具有重要的理论意义和应用价值。
目前,国内外关于各类传播行为的研究很多,但是聚焦于引发事故的不安全行为传播的研究较少,针对大型活动的群体行为传播更是凤毛麟角。人的不安全行为传播的研究主要集中在影响因素、传播规律、干预措施三个方面。在人的不安全行为传播的影响因素方面,相关研究成果较多,大多是基于各类事故模型展开的[5-7]。如:Hofmann等[8]在事故致因模型研究的基础上,首次提出了从事故致因角度揭示安全意识与不安全行为传播之间的关系;Seo等[9]首次将个人与组织因素结合得到安全文化、安全氛围与不安全行为之间的相互关系,但没有考虑环境背景。在人的不安全行为传播规律方面,利用改进后的连续或离散模型对人员不安全行为传播规律进行模拟试验的研究较多,如改进的传染病模型[10-12]、元胞自动机模型[13-14]等,但由于现实情况复杂,单一的离散或连续模型并不能反映真实情况下人员不安全行为的传播规律。在人的不安全行为传播干预措施方面,煤矿及建筑领域研究较多。如祁神军等[15]分析了激励和惩罚对工人不安全行为的干预效果,并由此提出了防范对策。然而,针对大型活动中人员不安全行为传播的干预研究尚属空白。
鉴于此,本文建立了一种基于群体视角下考虑安全培训效果的人员不安全行为传播模型,将元胞自动机的离散特征与传染病的连续特征结合起来,考虑群体中空间近邻的相互影响,并通过引入传播概率、潜伏时间和治愈时间来分析群体不安全行为传播规律和受到安全培训后人员的状态变化,仿真模拟研究了群体中安全意识、安全习惯和安全氛围对人员不安全行为传播过程的影响,以期为大型活动中拥挤踩踏事故的有效预防和科学应对提供依据。
1 大型音乐节活动中人员不安全行为传播特点
1.1 人的不安全行为分类
目前国内外学者对人的不安全行为的分类标准尚不统一,学者们一般都根据研究背景、研究角度以及研究目的不同定义对应的概念。如:青岛贤司[16]从行为结果的角度首次将人的不安全行为定义为确实已经造成或者是确实可能造成事故的行为,该定义得到了广泛认同;在此基础上,Reason[17]从人员不安全行为的来源出发,首先将不安全行为划分为“无意”“有意”两种。近年来,许多学者基于统计学方法归纳了人的不安全行为类型,如叶贵等[18]运用Hayashi 数量化理论,采用 MATLAB对工人不安全行进行了量化分类,将其分为技能偏差型、感知偏差型、习惯偏差型和程序偏差型 4 类。考虑到大型音乐节活动中人员不安全行为传播的特点,在综合各方面研究的基础上,将大型音乐节活动中人员不安全行为定义为活动中人员一系列可能直接导致拥挤踩踏事故发生的行为,出于省能、省时等动机或因受到群体不良氛围等的感染从而产生复制、跟从他人或演化出新的不安全行为的行为[19]。
1.2 人员不安全行为传播特点
学者们普遍认为行为传播是建立在沟通基础上的行为复制、扩散和演化的过程[20]。本文对数次大型音乐节活动开展了约一个月的现场跟踪调查,并访谈参与活动的歌迷、主办方、相关安全管理人员,通过对调研结果进行梳理,得到了文字、图片、语音、影像资料,在此基础上,总结出大型音乐节人员不安全行为的传播具有以下特点:
1) 人员不安全行为传播的非线性。大型音乐节活动人员不安全行为传播过程中歌迷之间或歌迷与歌手的反复交互作用中,人员不安全行为以及它们的属性均在发生变化[11],因此歌迷之间的相互影响不是简单的单向因果关系,而是主动的适应关系,由于歌迷所处的环境和感知均发生变化,而这些都将影响歌迷下一步的行为。但现实情况却往往是各种反馈作用的相互影响、彼此缠绕的复杂非线性关系的综合体现,并非是个体间的简单叠加[21]。
2) 人员不安全行为传播的复杂性。复杂性就是人员不安全行为传播处于有序和无序的一种混沌状态[22]。在大型音乐节活动中不安全行为的传播通常由几个人带动,然后带动几十人,之后在极短的时间内带动整个群体[23]。此外,群体中由于人员年龄、职业、性别、学历等方面存在差异,因此不同个体特征也对人员行为决策有直接的影响。由于音乐会现场人员情绪高涨,会主动与歌手和附近人员相互配合,自动进入混沌状态,此时群体中人员间不安全行为的传播会产生复杂现象。
3) 人员不安全行为传播结果的不确定性。不安全行为传播结果的不确定性是由人员和传播的复杂性变化所决定的,其传播过程不仅包括个体产生的不安全行为的传播,还包括群体之间不安全行为的随机传播。对一个人员产生的不安全行为传播而言,随着时间的推移或环境的变化,不安全行为传播受到的影响因素强度或种类可能会发生变化,最终导致传播结果的不确定性,且随着影响因素的增多,决定了人员不安全行为传播路径的复杂性和演化结果的不确定性会增强。
4) 人员不安全行为传播的可控性。虽然人员间不安全行为的传播具有非线性、复杂性、结果不确定性,但不安全行为的传播主要是由人的因素造成的,因此通过有效的事前安全培训提高人员安全能力,对人员不安全行为传播进行有效的管控,能够在一定程度上增强人员不安全行为传播的可控性。
2 大型音乐节活动中人员不安全行为传播模型建立
2.1 模型假设
大型音乐节活动中人员不安全行为传播通常发生在人群拥挤阶段,极易造成严重的人员伤亡[24]。由于行为传播与疾病传播的相似性,传染病模型在近年来也被广泛应用于人员不安全行为传播的研究中。如Jing等[25]、 Wan等[26]、张明媛等[27]分别在视频分析、行为试验、问卷调查的基础上,结合传染病模型对人员不安全行为传播机制展开了研究,并提出了相应的干预措施。也有学者利用元胞自动机(cellular-automaton,CA)的离散特点研究了人员不安全行为传播规律。如:马辉等[28]利用元胞自动机模拟了不同条件下邻域中工人不安全行为的传播扩散。因此,使用传染病模型与元胞自动机相结合来研究人员不安全行为的传播过程具有一定的理论依据。
在上述研究的基础上,本文采用SEIR(susceptible-exposed-infectious-recovered )模型尽可能接近实际状况对不安全行为传播过程中人员的状态进行研究,并根据元胞自动机离散的特点深入研究了安全培训对人员不安全行为传播的干预效果,由于人员不安全行为传播过程的复杂性,故对模型进行了如下假设:
1) 个体产生不安全行为后,同一范围内的其他个体均有可能受其影响,活动前进行安全培训能够约束人群中不安全行为的传播。
2) 根据个体感染不安全行为的程度,将其分为4类:没有发生但是有可能接触不安全行为的易感者S;已接触到不安全行为有可能复制模仿这类行为的潜伏者E;产生不安全行为并具有传播性的传播者I;感染过不安全行为但由于自身安全素养较好而拒绝产生不安全行为的免疫者R。
3) 某次活动中人群数量保持恒定,在t时刻的人群数量记为N(t),即S(t)+E(t)+I(t)+R(t)=N(t)。
4) 根据傅贵教授等[2]事故致因2-4 模型中对安全培训范围的定义,通过咨询相关专家并参考现有文献选取了安全意识、安全氛围、安全习惯3个关键性影响因素[29-31]。若个体的安全意识越高,不安全行为传播概率(β)越低;群体的安全氛围越好,不安全行为在个体中的潜伏时间(tq)也越低;个体的安全习惯越好,传播者转变为免疫者的治愈时间(tz)也越短。
2.2 模型描述
人员不安全行为传播模型建立在二维的元胞网格内,元胞大小设置为0.4 m×0.4 m,行为传播方式按扩展Moore邻域移动;对象元胞的状态受周围8个元胞的影响,且所有元胞的状态在转换规则的作用下同时进行;每个元胞有4种状态,分别为易感状态(S)、潜伏状态(E)、传播状态(I)、治愈状态(R),每种状态由不同颜色表示。建立的大型音乐节人员不安全行为传播模型如图1所示, 其中黑色元胞(i,j)为中心元胞,第(i-1,j-1)、(i-1,j)、(i+1,j-1)个元胞为绿色,第(i+1,j+1)个元胞为深灰色,第(i-1,j+1) 、(i,j-1)、(i+1,j)个元胞为红色,第(i,j+1) 个元胞为黑色。该模型的主要变量描述如表1所示。

表1 大型音乐节活动中人员不安全行为传播模型变量描述

图1 大型音乐节活动中人员不安全行为传播模型Fig.1 Propagation model of unsafe behavior of personnel in large-scale music festival
2.3 不安全行为传播规则
大型音乐节活动中在某时间阶段人员的状态取决于多个因素的影响[32],包括该成员及邻居在上个时间阶段的状态、成员自身特性、安全培训干预效果等因素,不安全行为从中心向外传播,传播开始阶段更多的是受邻近人员的影响,因果关系可表示为
S(i,j)(t+1)=F(S(i,j)(t)、S(i,j)L(t),λ(i,j)(t),Sλ(i,j)(t),β,tz,tq)
(1)
式中:S(i,j)(t)为细胞网格中上第(i,j)个元胞在第t个时间阶段的状态,且S(i,j)(t)={x| 0≤x≤ 3},x∈{0,1,2,3},其中“0”表明该成员为易感状态,用灰色表示,“1”表示该成员为传播状态,用红色表示,“2”表示该成员为治愈状态,用绿色表示,“3”表示该成员为潜伏状态,用黑色表示;λ(i,j)(t)为某时刻人员安全培训的干预程度,其可表示为
λ(i,j)(t)=N(i,j)(t)K+N(i,j)L(t)L
(2)
其中:N(i,j)(t)、N(i,j)L(t)分别为某时刻上下左右传播者数量和、左上左下右上右下传播者数量和;K、L为干预系数,为某时刻人员附近传播者安全培训的干预程度,取值范围为0到1。
Sλ(i,j)(t)为人员(i,j) 某一时刻自身特性,其为[0,1]之间的随机数,其可表示为
Sλ(i,j)(t)=rand(≠)
(3)
个体状态转换过程可分解为易感者规则、传播者规则、治愈者规则和潜伏者规则四部分:
1) 当活动前对人群进行安全培训时,确定易感者规则A1,如下式:
(4)
当活动前未对人群进行安全培训时,确定易感者规则A2,如下式:
(5)
(2) 确定传播者规则B,如下式:
(6)
(3) 确定治愈者规则C,如下式:
CS(i,j)(t)=2=S(i,j)(t+1)=2
(7)
(4) 确定潜伏者规则D,如下式:
(8)
3 模拟结果与分析
为了验证本文所建立的大型音乐节活动中人员不安全行为传播模型的实用性,假设某次音乐节活动场景如下:第一,初始状态下,除人群中心1名成员为潜伏者外,其余所有成员均为易感者;第二,人群中均为治愈者时,视为不安全行为传播过程结束,即人群不再产生新的不安全行为;第三,该场景下元胞网格为100×100(假设某次参加活动人员数量为10 000人),以时间步T为单位,步长为1 s。通过对以上假设的模拟,从安全培训的三个方面,即安全意识、安全氛围、安全习惯对人员不安全行为传播过程的影响进行不同时间段的试验模拟。
3.1 安全培训对人员不安全行为传播过程的影响
未对人群进行安全培训时,引用式(5)中的A2易感者规则;对人群进行安全培训时,引用式(4)中的A1易感者规则。基于此,设置参数λ(i,j)(t)如下:K=0.85,L=0.55,β=0.6,tq=30 s,tz=10 s,并记录两种规则下各时间段人员不安全行为传播过程的模拟结果以及150 s内4种状态人群数量随时间的变化情况,如图2至图5所示。

图2 未对人群进行安全培训时各时间段人员不安全 行为传播过程的模拟结果Fig.2 Simulation results of unsafe behavior propagation process at different time periods without safety training for the crowd
由图2和图3可知:在未对人群进行安全培训时,无论是在不安全行为传播的开始还是在结束阶段,不安全行为在人群中表现出来的状态始终非常混乱,这是因为在一个固定的环境中绝大部分人都习惯于学习周围人的行为,虽然偶尔由于自身特性会产生一些随机性的变化,但在不安全行为传播过程结束之前几乎没有可能去打破这种平衡,且在不安全行为传播过程中潜伏者数量占比较大,人群不安全行为在短时间内始终无法消除;而对人群进行安全培训后,不安全行为传播呈现一定的规律性,这是因为人群不安全行为传播过程中潜伏者数量占比较小,受到安全培训的大多数人不会轻易产生或传播不安全行为。

图3 对人群进行安全培训时各时间段人员不安全 行为传播过程的模拟结果Fig.3 Simulation results of unsafe behavior propagation process at different time periods without safety training for the crowd
通过对比图4与图5可知:通过对人群进行安全培训后易感者数量变化趋势不大,治愈者数量的增长速率变快,潜伏者数量迅速下降的同时,其峰值也随之变小;传播者数量变化与潜伏者相似,具有波动性,但传播者数量峰值在不安全行为传播前期未超过潜伏者,达到峰值以后趋于平稳,而其在不安全行为传播后期消失速率较潜伏者更快,随着时间的演变,不安全行为传播逆转的空间也越来越狭小。
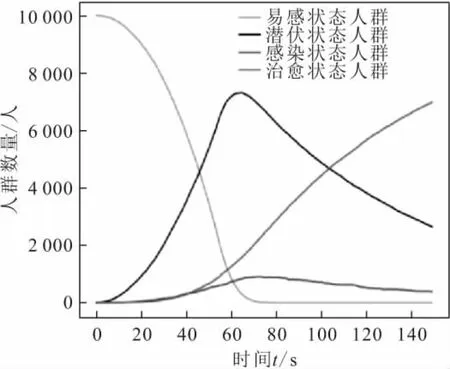
图4 未对人群进行安全培训时150 s内4种状态人群 数量随时间的变化Fig.4 Change curves of the number of people in four states in 150 s without safety training for the crowd
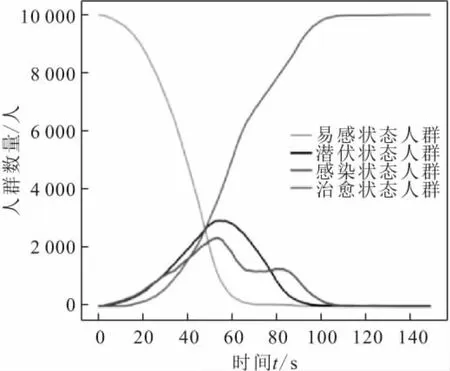
图5 对人群进行安全培训时150 s内4种状态人群数量 随时间的变化曲线Fig.5 Change curves of the number of people in four states in 150 s during safety training for the crowd
3.2 提升安全意识对人员不安全行为传播过程的影响
为了研究安全意识对人员不安全行为传播的影响,设置参数λ(i,j)(t)如下:K=0.85,L=0.55,tq=30 s,tz=10 s,记录传播概率β分别为0.4、0.2时各时间段人员不安全行为传播过程的模拟结果以及300 s内4种状态人群数量随时间的变化情况,如图6至图9所示。

图6 传播概率β为0.4时各时间段人员不安全行为 传播过程的模拟结果Fig.6 Simulation results of the propagation process of unsafe behaviors with the propagation probability βof 0.4
由图6和图7可知:与图3相比,随着安全意识的提升即传播概率的减小,原有人员不安全行为传播规律被打破,人群在安全意识提升的影响下,不安全行为传播范围得到遏制;随着时间的变化,人员不安全行为的传播呈病毒状,从中心向外逐渐恢复,最边缘的潜伏者和传播者逐渐向外扩散;当β=0.4时,此时虽然人员不安全行为传播范围进一步缩小[图6(a)、(c)],但还具有扩散的能力;当β=0.2时,治愈者和潜伏者一起将易感者和传播者隔离开,人员不安全行为传播范围进一步缩小[图7(a)、(c)]。

图7 传播概率β为0.2时各时间段人员不安全行为 传播过程的模拟结果Fig.7 Simulation results of the propagation process of unsafe behaviors with the propagation probability β of 0.2
通过对比图8与图9可知:随着安全意识的提升,即传播概率的减少,4种状态人群数量变化的波动性更加明显,治愈者数量增加的速率与易感者数量下降的速率基本持平,传播者与潜伏者在人群中始终维持在一个很低的数量,且不安全行为传播过程中传播者数量始终低于潜伏者数量;4种状态人群数量的变化皆呈现微弱的波动性,随着易感者和治愈者的数量缓慢下降,潜伏者和传播者数量维持在一个较低的水平;当β=0.4时,人员不安全行为传播过程结束的时间在200 s左右,群体中潜伏者的数量始终略大于传播者数量;当β=0.2时,300 s内人员不安全行为传播过程仍未结束。
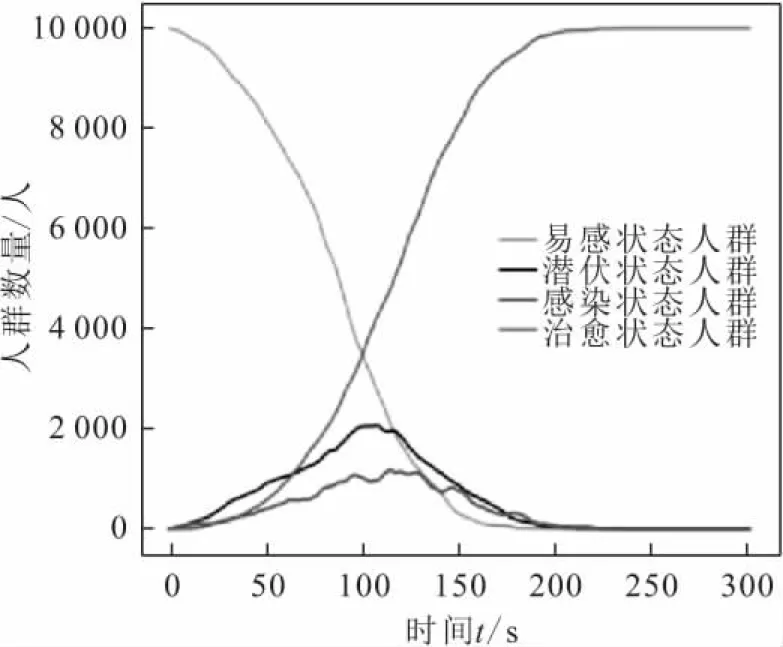
图8 传播概率β为0.4时4种状态人群数量随时间 的变化曲线Fig.8 Variation curves of the number of people in four different states over time with the propagation probability β of 0.4
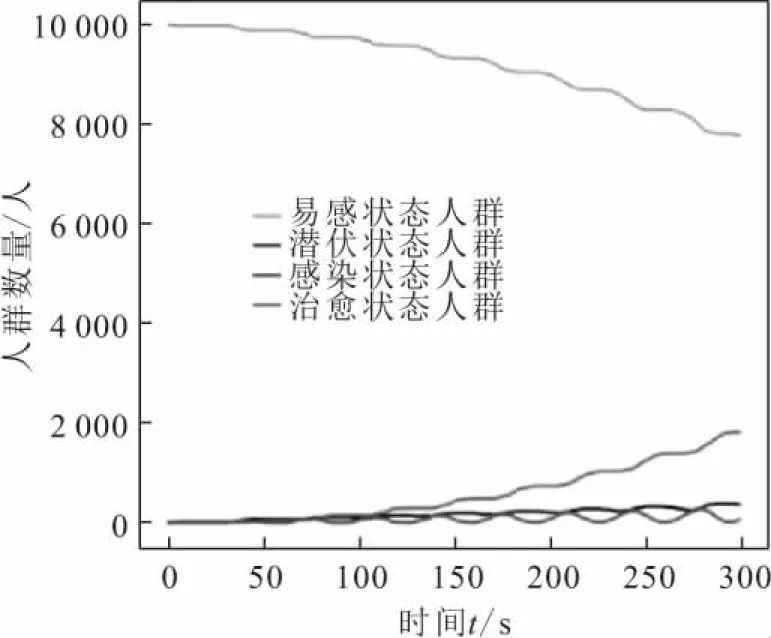
图9 传播概率β为0.2时4种状态人群数量随时间 的变化曲线Fig.9 Variation curves of the number of people in four different states over time with the propagation probability β of 0.2
3.3 营造安全氛围对人员不安全行为传播过程的影响
为了研究安全氛围对人员不安全行为传播过程的影响,设置参数λ(i,j)(t)如下:K=0.85,L=0.55,β=0.4 s,tz=10 s,记录tq=10、50 s时各时间段人员不安全行为传播过程的模拟结果以及300 s内4种状态人群数量随时间的变化情况,如图10至图13所示。

图10 潜伏时间tq为10 s时各时间段人员不安全行为 传播过程的模拟结果Fig.10 Simulation results of the propagation process of unsafe behaviors in each period with the latency timetqof 10 s
通过对比图10与图11可知:随着安全氛围的提升,即潜伏时间的减小,人员不安全行为传播范围没有发生明显的变化,潜伏者始终占据人群的大多数,潜伏者数量众多,已经治愈的个体周围依然存在大量的潜伏者[图11(a)、(b)],导致人群中心不安全行为开始了二次传播[图11(c)];随着时间的变化,潜伏者和传播者作为一个屏障将易感者和治愈者隔离开[图10(a)、(b)];从图10(b)到图10(c)时,人员不安全行为传播基本结束,潜伏者消失的时间明显提前;t=80 s时,tq=10 s中的潜伏者已经都转变为治愈者,即人员不安全行为传播过程基本结束,但tq=50 s中的潜伏者数量还维持在较高的比例。

图11 潜伏时间tq为50 s时各时间段人员不安全行为 传播过程的模拟结果Fig.11 Simulation results of the propagation process of unsafe behaviors in each period with the latency timetqof 50 s
通过对比图12与图13可知:随着安全氛围的提升,即潜伏时间的减少,易感者数量减少速率基本保持不变,治愈者数量增加速率变快;传播者数量出现峰值的时间逐渐提前,潜伏者的数量峰值减小但传播者的数量峰值增大,与此同时传播者的数量峰值比潜伏者的数量峰值高,传播者数量随时间的变化曲线由双峰曲线变为单峰曲线;当tq=50 s时,人员不安全行为传播过程结束的时间在120 s左右,当tq=10 s时,人员不安全行为传播过程结束的时间在90 s左右。

图12 潜伏时间tq为10 s时4种状态人群数量随 时间的变化曲线Fig.12 Variation curves of the number of people in four different states over time with the latency time tq of 10 s
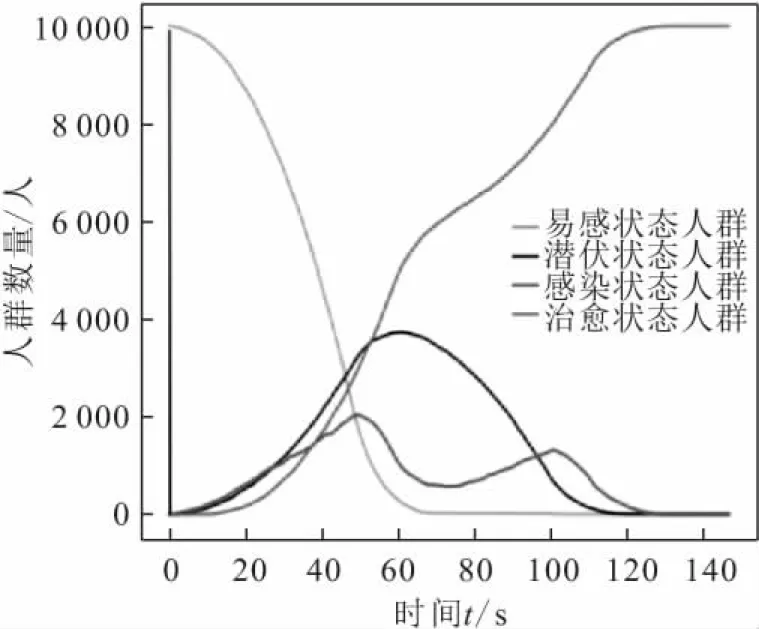
图13 潜伏时间tq为50 s时4种状态人群数量随时间 的变化曲线Fig.13 Variation curves of the number of people in four different states over time with the latency time tq of 50 s
3.4 增强安全习惯对人员不安全行为传播过程的影响
为了研究安全习惯对人员不安全行为传播过程的影响,设置参数λ(i,j)(t)如下:K=0.85,L=0.55,β=0.4,tq=30 s,记录tz=30、50 s时各时间段人员不安全行为传播过程的模拟结果以及300 s内4种状态人群数量随时间的变化情况,如图14至图17所示。

图14 治愈时间tz为30 s时各时间段人员不安全行为 传播过程的模拟结果Fig.14 Simulation results of the propagation process of unsafe behaviors in each period with the cure time tz of 30 s
通过对比图14与图15可知:随着安全习惯的增强,即治愈时间的缩短,人员不安全行为传播范围变化不大,传播者成为群体的大多数;当t=40 s时,tz=50 s的人群中依旧没有治愈者的出现,tz=10 s的人群中已经产生治愈者,证明人群中已经有个体从传播者恢复为治愈者,说明安全习惯可以有效约束不安全行为传播过程中传播者的数量。

图15 治愈时间tz为50 s时各时间段人员不安全行为 传播过程的模拟结果Fig.15 Simulation results of the propagation process of unsafe behaviors in each period with the cure time tz of 50 s
通过对比图16与图17可知:随着安全习惯的提升,即治愈时间的减少,易感者、潜伏者的数量变化不明显,传播者的数量峰值明显变小,这导致治愈者数量增加的速率变大,即绿色曲线更加陡峭,传播者的数量峰值增大,传播者数量随时间的变化曲线由双峰曲线变为单峰曲线;当tz=50 s时,人群中治愈者数量上升的起点在60 s左右,且人员不安全行为传播过程结束的时间在140 s左右,而当tz=30 s时,人群中治愈者数量上升的起点在40 s左右,人员不安全行为传播过程结束的时间在120 s左右。

图16 治愈时间tz为30 s时4种状态人群数量随时间 的变化曲线Fig.16 Variation curves of the number of people in four different states over time with the cure time tz of 30 s

图17 治愈时间tz为50 s时4种状态人群数量随时间 的变化曲线Fig.17 Variation curves of the number of people in four different states over time with the cure time tz of 50 s
4 结 论
本文建立了一种基于群体视角下考虑安全培训效果的人员不安全行为传播模型,将元胞自动机的离散特征与传染病的连续特征结合起来,考虑群体中空间近邻的相互影响,并通过引入传播概率、潜伏时间和治愈时间来分析群体不安全行为传播规律和受到安全培训后人员的状态变化,仿真模拟研究了群体中安全意识、安全习惯和安全氛围对人员不安全行为传播过程的影响,得到的主要结论如下:
1) 大型音乐节活动前进行安全培训可以有效约束人员不安全行为的传播,提升个体的安全意识,从而降低不安全行为传播过程中潜伏者和传播者的数量,缩小人员不安全行为的传播范围。
2) 个体的安全意识越高,不安全行为的传播范围越小;群体的安全氛围越好,传播者传播速度变快,潜伏者传播速度变慢,对人员不安全行为传播的影响越小;个体的安全习惯越好,即传播者和潜伏者的传播速度越快,人员不安全行为的传播过程结束的时间越早。
3) 本文模型能够应用于现实中大型活动中人员不安全行为传播过程的模拟,为大型活动前的安全培训提供新的思路和方法。

