数据时间维度对火灾形势预测精度的影响
王 洁,李天明,余淞洋,陆凯华,姜学鹏
(1.武汉科技大学资源与环境工程学院,湖北 武汉 430081; 2.湖北省工业安全工程技术中心,湖北 武汉 430081;3.武汉科技大学安全与应急研究院,湖北 武汉 430081;4.中国舰船研究设计中心,湖北 武汉 430081;5.中国地质大学(武汉) 工程学院,湖北 武汉 430074)
火灾是严重威胁公共安全和社会发展的主要事故之一。火灾风险评估、火灾形势发展趋势预测等研究都是为了给决策者制定消防规划提供依据,从而提升城市韧性[1]、降低火灾的发生概率。其中,火灾形势发展趋势预测以火灾形势评价结果为基础,该评价结果主要是建立在历史火灾4项指标(火灾发生次数、死亡人数、受伤人数和直接经济损失)基础上[2]。但随着经济的快速发展,火灾致因更加复杂多样,火灾风险日益增加[3],仅考虑火灾4项指标已无法客观地评价火灾形势[4],也无法精准预测火灾形势发展趋势。因此,合理使用火灾形势评价指标和结果,准确地预测火灾形势发展趋势,对城市火灾预防和可持续发展具有重要意义。
目前对于火灾形势发展趋势预测的研究主要集中在评价方法和评价指标方面,发展趋势预测方法以灰色预测模型为主。如:刘海生等[5]在消除了火灾4项指标量纲影响的基础上,运用主成分分析法评价得出截至2008年我国火灾形势呈现下降趋势;安振宁等[6]、戴仕杰等[7]运用多属性综合评价法解决了采用火灾4项指标评价火灾形势的局限性;周白霞[2]、王子冈[8]总结了采用火灾4项指标评价火灾形势存在的不足,并对重构综合评价体系提出了相关建议;滕金苹[9]在火灾4项指标基础上增加了烧毁面积和受灾户数指标来对火灾形势进行评价;Luo等[10]在火灾4项指标基础上增加了火灾发生率、死亡率、受伤率、人均损失和每次火灾损失指标,并运用主成分分析法评价得出截至2017年我国火灾形势总体平稳;王郭社等[11]从火灾4项指标、火灾经济指标和重特大火灾指标三个方面共12个指标出发,运用主成分分析法对我国各省火灾形势进行了综合评价。
综上可见,大部分学者在改进评价方法、重构评价指标、增加相关指标等方面优化评价及预测结果时,其所使用的评价指标都是以年为时间维度的,鲜有学者采用以季、月为时间维度的评价指标来评价火灾形势并预测其发展趋势。因此,本文拟以年、季、月为时间维度的3组火灾统计数据为历史数据,应用主成分分析法得到相应的火灾形势评价结果,并根据评价结果,结合灰色理论,构建相应的GM(1,1)预测模型,通过相关判据确定何种时间维度构建的GM(1,1)预测模型的预测精度最优,进而应用该模型预测某地火灾形势发展趋势,从而为政府制定有效的消防规划提供更精准的依据。
1 火灾形势综合评价
1.1 评价指标
本文综合考虑了评价指标的局限性和众多学者的研究成果,为了准确且全面地评价我国火灾形势,将火灾发生次数(起)、火灾发生率(起/十万人口)、死亡人数(人)、死亡率(人/百万人口)、受伤人数(人)、受伤率(人/百万人口)、直接经济损失(万元)、经济损失率(元/万元国内生产总值)和每次火灾经济损失(元)共9个指标作为火灾形势发展趋势预测的指标。通过文献[12-15]分别收集上述指标以年、季、月为时间维度的3组历史数据,详细数据见表1、表2和表3。

表1 以年为时间维度的9项指标历史数据
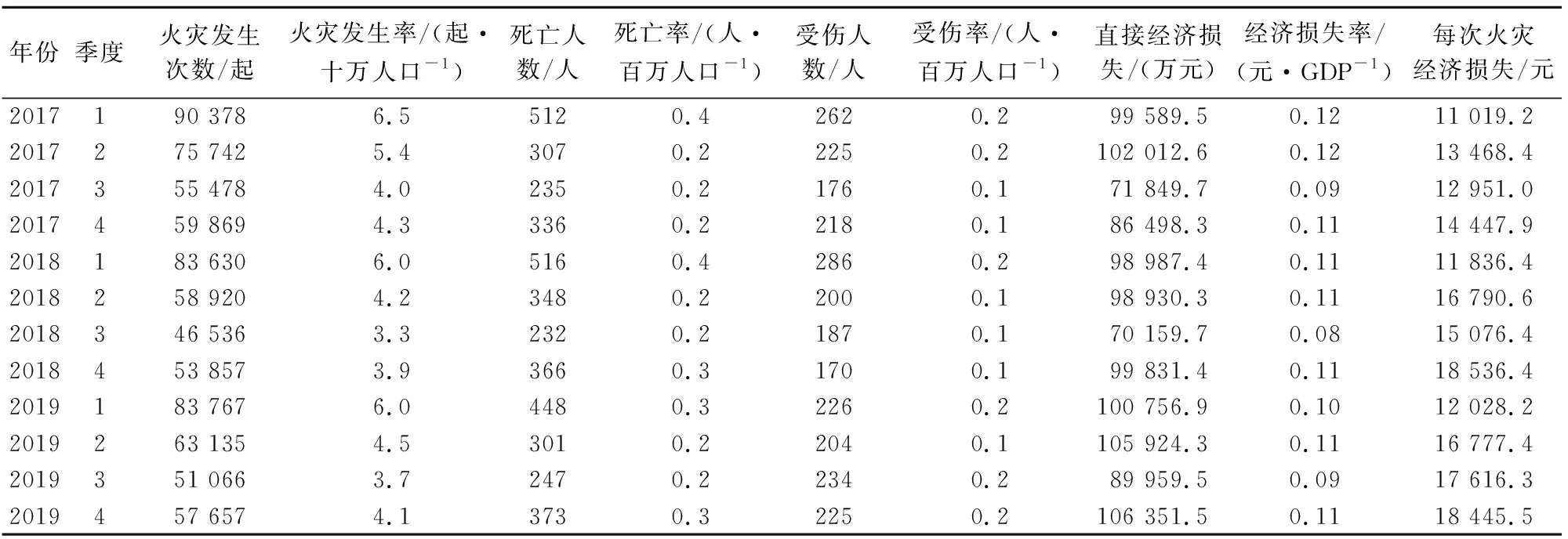
表2 以季为时间维度的9项指标历史数据
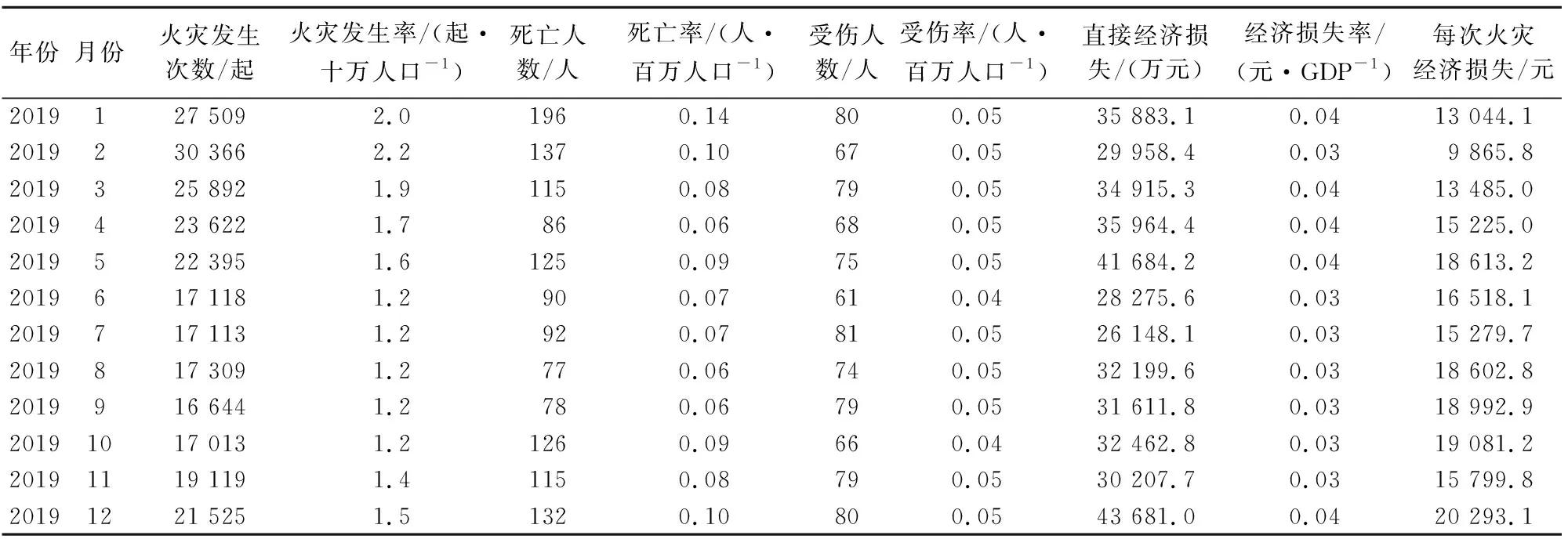
表3 以月为时间维度的9项指标历史数据
1.2 评价方法
对几种常用的火灾形势评价方法的原理、优缺点和适用场景进行对比分析,其结果详见表4。
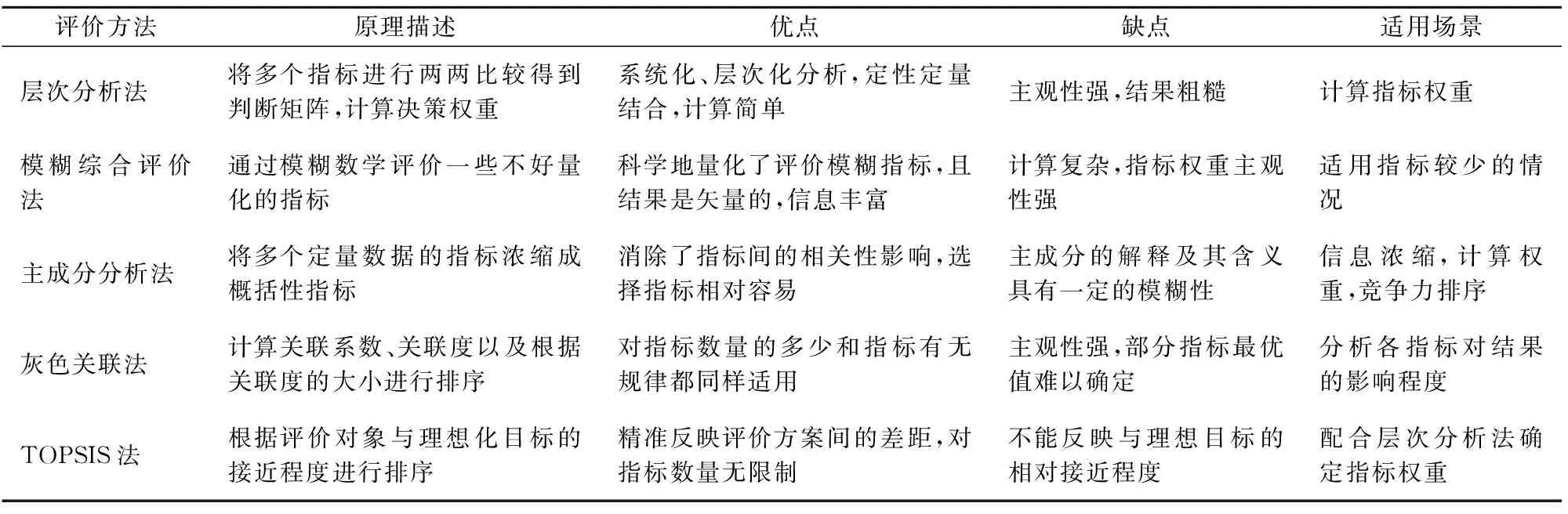
表4 常见的火灾形势评价方法的对比分析
由表4可知:在对多个定量指标进行评价时,主成分分析(PCA)法通过重构具有相关性的指标使其成为相互独立的新指标——主成分,在消除相关性影响的同时降低了维度和冗余变量[10],能够很好地将多个定量指标浓缩为有效信息,却不受主观意识的影响。因此,本文选取PCA对我国火灾形势进行综合评价。
假设有m个评价指标和n个评价对象,PCA的评价步骤如下[16]:
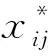
2) 计算相关系数矩阵R=(rij)m×m。其中,rij为第i个评价指标与第j个评价指标的相关系数,其计算公式为
(1)
3) 计算R的特征值λm及其相应的特征向量μm。其中,μj= (μ1j,μ2j,…,μnj)T。由特征向量组成m个新的指标变量:
(2)
式中:y1为第一主成分;y2为第二主成分;…;ym为第m主成分。
4) 选择p(p≤m)个主成分,计算λj的信息贡献率a和累计贡献率b(b≥90%)[17],其计算公式如下:
(3)
(4)
1.3 评价结果分析
基于年、季和月3种时间维度的9项指标,运用主成分分析法提取不同数量(分别为2、4和4)的主成分,其累计贡献率b分别为93.85%、95.74%和97.14%,均大于90%,最终分别得到3种时间维度下火灾形势评价结果,其可视化如图1所示。为了方便火灾形势发展趋势预测,对评价结果进行了归一化处理,其结果见表5。归一化处理公式为

图1 以年、季和月为时间维度的9项指标综合评价得分Fig.1 Comprehensive evaluation results of nine indicators in time dimension of year,quarter and month
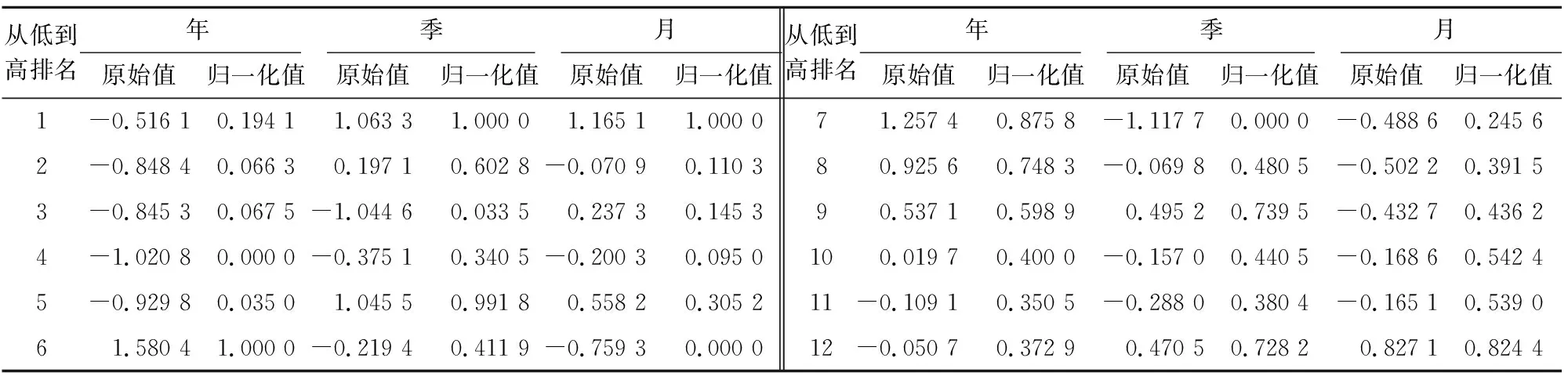
表5 以年、季和月为时间维度的9项指标综合评价得分归一化处理结果
x′=[x-min(x)]/[max(x)-min(x)]
(5)
由图1可以看出:2008—2019年12年间,2013年的火灾形势最为严峻,2011年火灾形势平稳,2013年后火灾形势总体呈下降趋势;2017—2019年12个季度中,2017年第一季度的火灾形势最为严峻,2018年第三季度的火灾形势平稳,火灾形势总体呈周期性变化,且每年的第一季度火灾形势均较为严峻,第三季度火灾形势均平稳;2019年12个月中,1月份的火灾形势最为严峻,6月份的火灾形势平稳,6月份后火灾形势呈上升趋势。
综上所述,不同时间维度的指标数据所得出的火灾形势发展规律是不相同的。
2 火灾形势发展趋势预测模型
合理运用预测模型对火灾发展趋势进行预测,对制定有效策略、优化消防资源配置、减少火灾的发生具有一定的理论指导意义。目前,学者们采用多种预测模型对火灾形势发展趋势进行了预测,如灰色预测模型、指数平滑法、时间序列预测法、Markov预测法、神经网络等[18-22],其优缺点对比如表6所示。
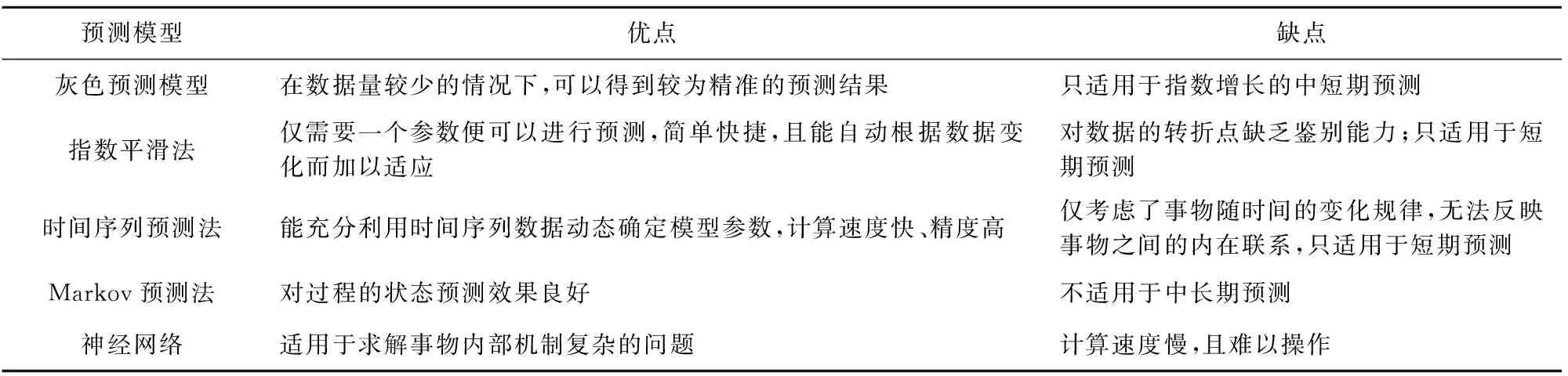
表6 常用的火灾形势发展趋势预测模型的对比分析
由表6可知:灰色预测模型能够利用较少的数据得到精准的预测结果,符合火灾数据因获取途径少而难以获取大量相关数据的现状,且由于本文根据时间维度只向后预测一个数据,即2020年、2020年的第一季度和2020年的1月,属于短期预测,加之火灾致因复杂多样,有些因素难以量化[18],符合灰色系统理论对象特征[5]。因此,本文选取灰色预测模型中常用的GM(1,1)预测模型对火灾形势发展趋势进行预测。
2.1 GM(1,1)预测模型
GM(1,1)预测模型是灰色预测理论的基本模型,该模型由一个单变量的一阶微分方程构成。GM(1,1)预测模型的构建步骤如下[23]:
首先,设原始序列为X(0)=(x(0)(1),x(0)(2),…,x(0)(n)):对X(0)进行累加处理,生成1-AGO序列X(1)=(x(1)(1),x(1)(2),…,x(1)(n))和X(1)的紧邻均值序列Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))。其中:
(6)
(7)
然后,建立灰色微分方程x(0)(k)+az(1)(k)=b,其中a为发展系数,b为灰作用量,且a、b满足[ab]T=(BTB)-1BTY的关系。其中:
最后,得到GM(1,1)的预测模型:
(8)
2.2 模型精度检验
本文选取后验差比值C、小误差概率P和平均相对误差Δ来判定模型的预测精度等级[24],GM(1,1)模型预测精度评判标准见表7。其中:
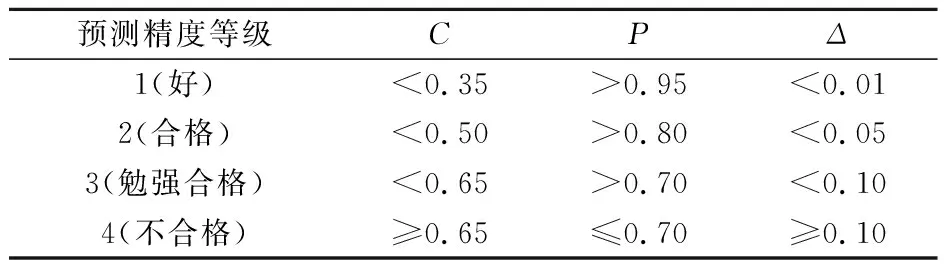
表7 GM(1,1)预测模型精度判定标准
(9)
P=p{|Δ(0)(k)-Δ(0)|<0.674 5S1}
(10)
(11)

3 实例计算与分析
3.1 建立GM(1,1)预测模型
本文将通过控制数据量Q来建立表5中3种时间维度评价结果(分别记作y、q、m)的GM(1,1)预测模型。其中,Q是指与预测时间维度相同且相邻的若干历史数据个数,如Qy=Qq=Qm=4分别为2016—2019年、2019年的4个季度和2019年的9-12月。当Q一定时,不同时间维度的指标数据所覆盖的时间跨度是不同的,会受经济、政策以及环境等因素的影响,但指标数据本身是火灾作用于社会环境的直接结果[6],环境中包含了上述影响因素。因此,本文仅且只需要对数据量进行探究。其技术路线如图2所示。

图2 研究技术路线Fig.2 Technical route of the research
因GM(1,1)模型不适合用于预测大量数据,结合本文数据情况,设定数据量3 ≤Q≤12,建立的模型的检验结果和精度等级,见表8。
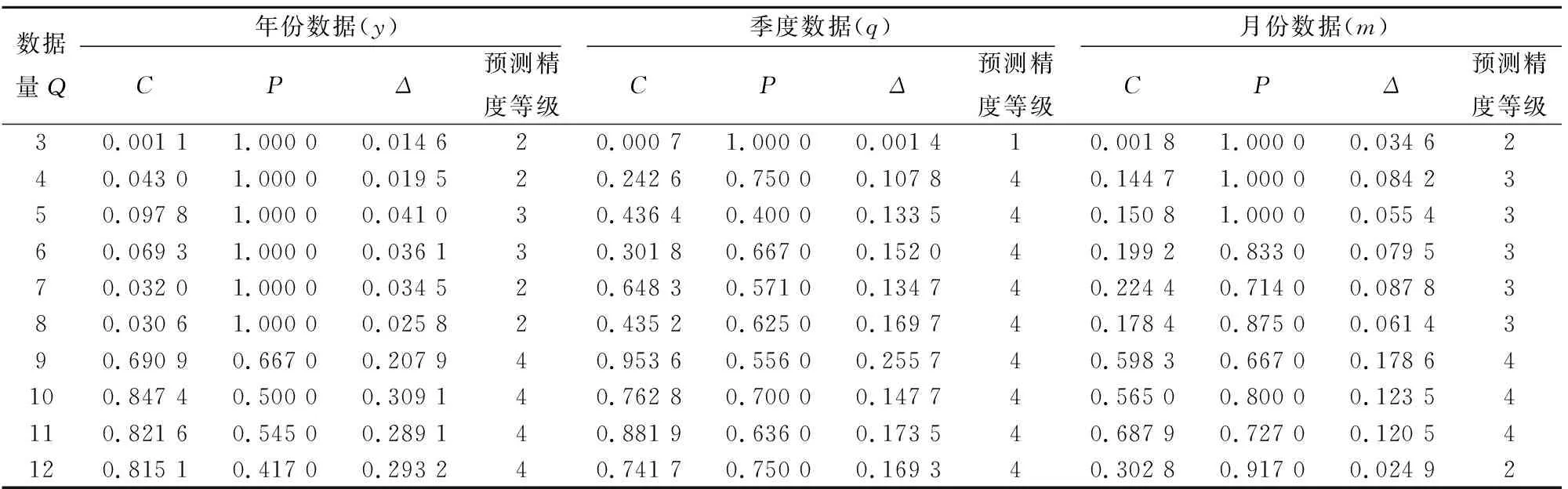
表8 不同时间维度火灾历史数据所建立GM(1,1)预测模型的C、P和Δ值
3.2 结果分析与讨论
由表8可知:相同数据量下,不同时间维度的火灾历史数据所建立的GM(1,1)模型的预测精度差异较大。记(di)j=(ij)max-(ij)min,i=C、P、Δ,j=y、q、m,得到以下关系式:
(dC)q>(dC)y>(dC)m,
(dP)q>(dP)y>(dP)m,
(dΔ)y>(dΔ)q>(dΔ)m.
由关系式可知,季度数据所建立的GM(1,1)模型的预测精度差异最为明显,年份数据次之,月份数据最小。
综合考虑数据量和年、季、月时间维度,将其划分为3个区域分别进行分析,具体分析如下:
1) 区域①:当Q=3时,Cq

图3 2019年第2-4季度火灾历史数据所建立GM(1,1)模型的拟合情况Fig.3 Fitting of the GM(1,1) model based on historical fire data from the second to fourth quarters of 2019
2) 区域②:当4≤Q≤8时,以年份数据建立的GM(1,1)模型检验值优于季度数据和月份数据,且当Q=4、7、8时,以年份数据建立的GM(1,1)模型的预测精度等级均为2级,因C8
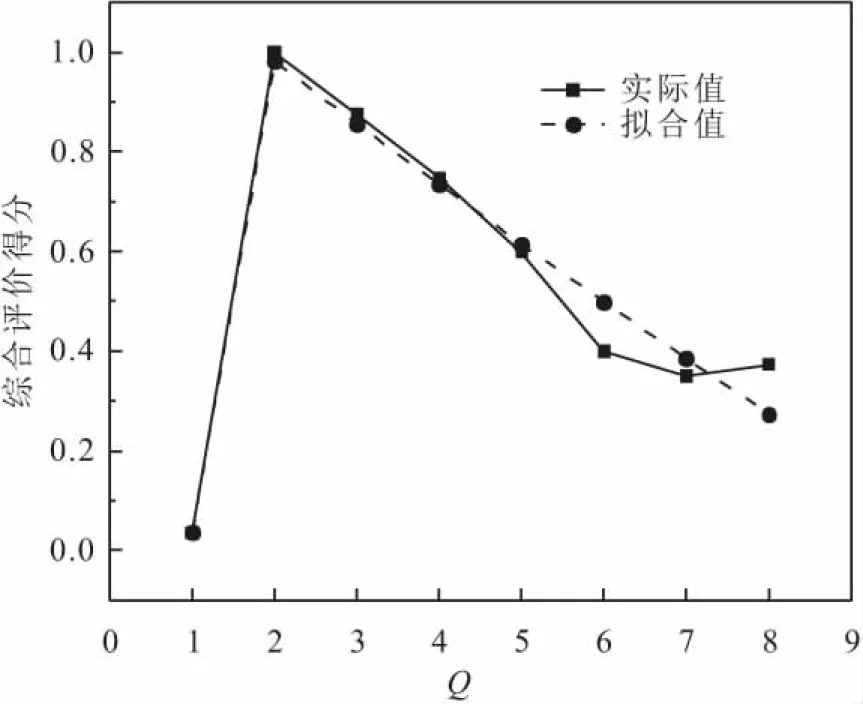
图4 2012-2019年火灾历史数据所建立GM(1,1)模型的拟合情况Fig.4 Fitting of the GM(1,1) model based on historical fire data from 2012 to 2019
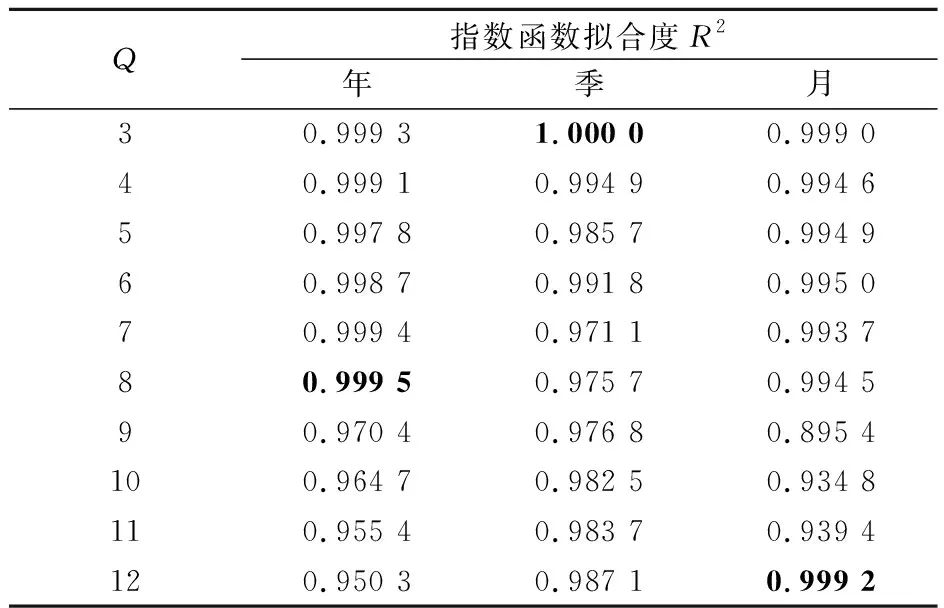
3) 区域③:当8 图5 2019年1-12月份火灾历史数据所建立GM(1,1)模型的拟合情况Fig.5 Fitting of the GM(1,1) model based on the histo- rical fire data from January to December of 2019 综上,分别得到了以年、季、月为时间维度的火灾历史数据建立的3个GM(1,1)预测模型,其拟合值与实际值的对比情况如图3至图5所示。 由图3至图5可以看出:与其他两个GM(1,1)预测模型相比,2019年第2-4季度火灾历史数据所建立的GM(1,1)预测模型的拟合值与实际值的吻合程度最高,能准确反映出火灾形势综合评价得分随季度的变化规律及趋势,且该模型的平均预测精度高达99.98%,非常适合用其进行火灾形势发展趋势预测;而基于2012—2019年和2019年1-12月份火灾历史数据建立的GM(1,1)预测模型,也能够大致反映出火灾形势与对应时间维度的关系,也有着较高的平均预测精度,分别为96.74%、95.53%。 利用其预测模型分别预测得到2020年全年、第1季度和1月份的火灾形势综合评价得分分别为0.166 0、0.949 1和0.733 5。由预测结果可知,2020年火灾形势总体平稳,但第1季度和1月份的火灾形势较为严峻,相关部门应在2020年第1季度和1月份加强火灾监管。因此,仅仅对年的火灾形势进行预测不能为决策者制定精准有效的消防规划提供依据。以上3组模型在相应的条件下均可以作为预测模型,但根据季度和月份预测模型的预测结果可以细化完善消防规划,由于其精准到季和月,因此可以更好地预防火灾发生。该研究结果既说明了以季和月为时间维度的数据包含着很多信息,有着很大的利用价值,又验证了数据的时间维度对GM(1,1)模型的预测精度有着较大的影响,尤其是季度数据。 模型预测精度差异产生的原因可能是数据波动较大,如:年份数据在2013年骤增,然后逐年下降;季度数据呈周期性变换,且每年第1季度、第3季度均为最高和最低;月份数据在5月份骤降,然后逐月上升,而GM(1,1)模型无法很好地处理这种数据波动。从其建模原理角度来说,原始数据经一系列不改变本质的处理后无法形成规律性较强的数据序列。因此,对图1中的综合评价得分按数据量分别进行累加处理(详见第2.1节),然后进行指数函数拟合,得到的指数函数拟合度R2见表9。 表9 累加处理后各评价结果的指数函数拟合度R2 从表9中得到了与检验标准判断一样的结果,即:当Q=3时,季度数据的R2值(1.000 0)最高;当Q=8时,年份数据的R2(0.999 5)最高;当Q=12时,月份数据的R2(0.999 2)最高,并对其进行了可视化处理,其结果见图6。 图6 3组拟合度最好的数据可视化处理结果Fig.6 Visualizaiton result of three best-fitting data 通过归纳总结后可以发现,R2值越接近1,模型的预测精度等级越高。当R2≥0.999 0时,模型的预测精度等级最低为2级,1级和2级的临界值需要更多模型加以确定;当R2<0.999 0时,模型的预测精度较低(3级或4级)。因此,在构建GM(1,1)预测模型前可以先用R2值对其进行初步筛选,这样可大大减少计算量,提高预测效率。 1) 基于年、季和月3种不同时间维度的火灾历史统计数据,运用主成分分析法得出了3种不同发展规律的火灾形势评价结果。其中,年份数据从2013年开始总体呈下降趋势;季度数据总体呈周期性变化,第1季度火灾形势均较为严峻;月份数据前半年呈下降趋势,后半年呈上升趋势。 2) 基于火灾形势评价结果,通过控制数据量Q,验证了在GM(1,1)模型中不同时间维度的火灾历史数据对火灾形势发展趋势的预测精度有着较大的影响,其中季度数据最为明显。当Q=3时,季度数据更适合火灾形势发展趋势预测,模型的预测精度为1级,预测精度高达99.98%;当Q=8时,年份数据更适合火灾形势发展趋势预测,模型的预测精度为2级,预测精度为96.74%;当Q=12时,月份数据更适合火灾形势发展趋势预测,模型的预测精度为2级,预测精度为95.53%。 3) 运用以年、季、月为时间维度的火灾历史数据构建的3种GM(1,1)预测模型,得到了2020年全年、第1季度和1月份的火灾形势综合评价得分分别为0.166 0、0.949 1和0.733 5,火灾形势不尽相同。因此,仅仅考虑年的火灾形势发展趋势已无法很好地预防火灾的发生,而基于季度和月份数据建立的模型预测结果,可以为决策者制定精准到季度或月份的详细消防规划提供一定的理论基础,从而合理配置消防资源与力量,最大程度地发挥其作用,更有效地减少火灾的发生次数及其损失。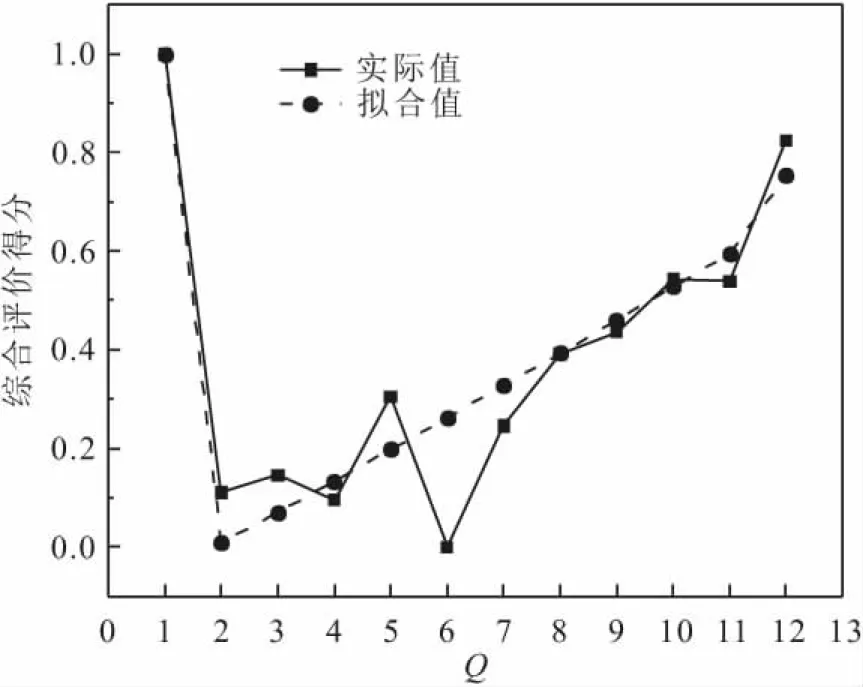

4 结 论

