TOPSIS-AISM模型在基坑支护方案优选中的应用
景文琪,宋绍溥,李 杨,罗学东*
(1.中铁二十一局集团轨道交通工程有限公司,山东 济南 250021;2.中国地质大学(武汉)工程学院,湖北 武汉 430074)
随着城市的不断扩张,基坑工程也正向深、大的方向发展,相应的基坑支护工程施工环境也越来越复杂[1],而合理的基坑支护方案除了可以降低环境因素对基坑施工安全的影响,还可以避免基坑变形过大对周围建筑以及地下管道产生的危害,从而保障人民的生命与财产安全,因此在基坑施工过程中有必要对基坑支护方案进行合理选择。
近年来,众多学者对基坑支护方案优选方法进行了大量的研究。如:廖瑛等[2]在运用层次分析方法的基础上,结合模糊数学建立了深基坑支护方案模糊决策矩阵,充分考虑了基坑支护方案具有模糊性的特点,并利用数学的方法将主观判断进行了客观修正;何满潮等[3]基于大量的实际案例,运用BP神经网络对基坑支护方案进行了比对分析,并利用拓扑结构表示各决策因素的相互关系,使决策过程更加直观科学;孙秉珍等[4]将TOPSIS(technique for order preference by similarity to an ideal solution)方法应用于基坑支护方案优选中,并通过研究各基坑支护方案与理想方案之间的欧式距离,在空间层面对基坑支护方案的优劣进行了精准评价。
大量的工程实例分析表明,混合优化的决策方法与单一决策方法相比,具有更好的全局收敛性、效率和精度[5-6]。为此,本文首先将TOPSIS法与对抗解释结构模型(adversarial interpretative structural model,AISM)法相结合,建立TOPSIS-AISM夹逼对抗解释结构模型;然后引入拓扑学与博弈论思想,运用矩阵计算与哈斯图解将评价体系因素之间的相互关系以及各基坑支护方案与理想方案的空间距离进行直观表现;最后通过实际工程案例对该方法的合理性与科学性进行验证,以期为类似基坑工程提供参考。
1 模型介绍
1.1 TOPSIS法
TOPSIS法是多目标决策分析中一种常用的有效方法,其基本思想是计算目标方案与理想方案之间的接近程度值并进行排序,从而表示目标方案的优劣。传统TOPSIS法的建模流程,如图1所示。

图1 传统TOPSIS建模流程图Fig.1 Flowchart of traditional TOPSIS modeling
1.2 AISM法
AISM法是在解释结构模型(interpretative structural modeling,ISM)的基础上融入生成对抗网络(GAN)中的博弈对抗(adversarial)思想形成的一种模型方法。传统ISM法的作用是把任意包含许多离散的、无序的静态系统,利用系统要素之间已知的、但凌乱的关系解释出系统的内部结构[7-8],其表现形式为矩阵与图形,即通过矩阵表示系统内各因素间的已知关系,将存在优劣关系的目标对象用有向线段标识,以从因到果的方式求得因果可达序列,并用拓扑图层的方式对目标优劣进行描绘[9]。 AISM法在此基础上加入以原因为导向的排列,即由果索因求取因果可达矩阵,从而建立与ISM排列相对立的有向拓扑图[10]。由于通过结果优先与原因优先层级抽取的方式得到的有向拓扑层级图可能并不一致,因此通过对两者取交集可增加结果的科学性与合理性。AISM法的建模流程如下[10]:

其中:A为邻接矩阵;D为加入客观标准样本后的决策矩阵;M为布尔型关系矩阵;S为一般性骨架矩阵,从该矩阵中可以得出要素层级和要素间关系[10],从而得出一组UP/DOWN对抗性有向拓扑图。
1.3 TOPSIS-AISM夹逼对抗解释结构模型建立
本文将 TOPSIS法与AISM法相结合,构建了TOPSIS-AISM夹逼对抗解释结构模型。传统TOPSIS法的因素排序结果往往为直链型,对多维因素下排序的模糊性考虑不足。相对于传统TOPSIS法,该模型可将排序层级清晰表示出,明确各待选方案的优劣程度,同时对正、负理想解进行夹逼对抗解释,使具有明确直链形式的方案排序结果拓延到了具有跃迁性质不可比的方案排序结果[7,9],以体现评判过程中的模糊性。TOPSIS-AISM夹逼对抗解释结构模型的建模过程,如图2所示。
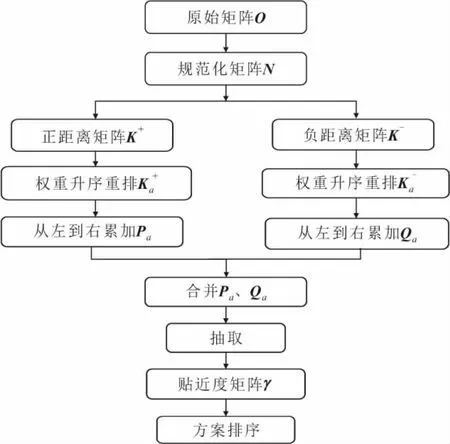
图2 TOPSIS-AISM夹逼对抗解释结构模型的建模流程图Fig.2 Modeling flowchart of TOPSIS-AISM pinch adversarial explanatory structural model
1.3.1 数据处理
根据工程实际情况选取n个评价指标建立评价指标体系与评价矩阵O=[oij]m×n,评价矩阵指标可分为正向指标与负向指标,其中正向指标数值越大越优,负向指标数值越小越优。由于指标属性与单位不同致使后续计算无法进行统一运算,因此需要对原始矩阵进行无量纲化处理,本文采用极差法对原始矩阵数据进行归一化处理,得到规范化矩阵N=[nij]m×n。具体计算公式如下:
正向指标为
(1)
负向指标为
(2)
归一化处理后原始矩阵指标统一为正向指标。
1.3.2 指标权重确定
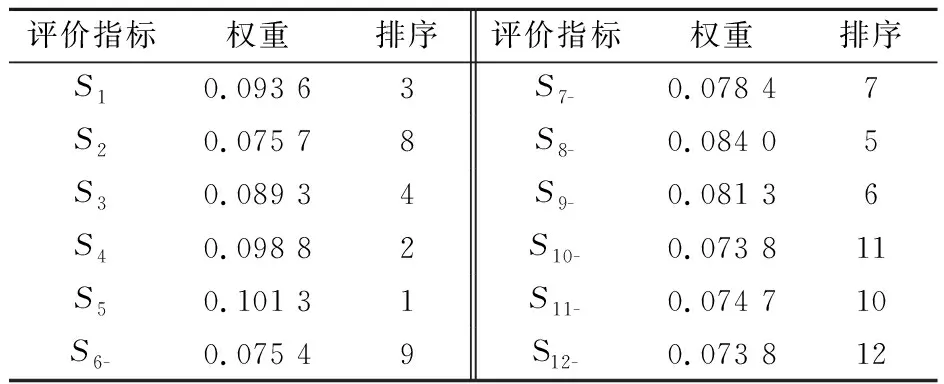
指标权重的合理确定是进行基坑支护方案决策优选的一个关键问题。目前指标赋权方法主要分为主观赋权法和客观赋权法两类:主观赋权法以层次分析(AHP)法为代表,该类方法主要通过专家评定界定各指标权重,往往具有较强的主观性[11];客观赋权法主要采用合理的数学方法对原始数据之间的关系进行分析处理,不依赖人的主观判断,有较强的数学理论依据[12]。本文采用客观赋权法中的CRITIC法[12]对评价指标进行赋权,得到各指标权重向量矩阵为W=[w1,w2,…,wn]T。
1.3.3 确定正、负理想方案
评价指标具有二维性,根据客观评判标准可求得正、负理想点向量矩阵,分别记为S+、S-,其中S+具有越大越优的特点,S-具有越小越优的特点。传统TOPSIS法正、负理想点矩阵可表示如下:
(3)
由于在方案选取过程中正、负理想点仅代表单个案例决策矩阵数据范围内的方案优劣,对广泛工程案例适用性不足,缺乏客观性,因此应结合专家学者意见并参考各工程案例对工程项目优劣方案制定客观标准,同时该标准在模型中应以层间要素出现与各待选方案做层级比较,以直观表现各待选方案的优劣程度。
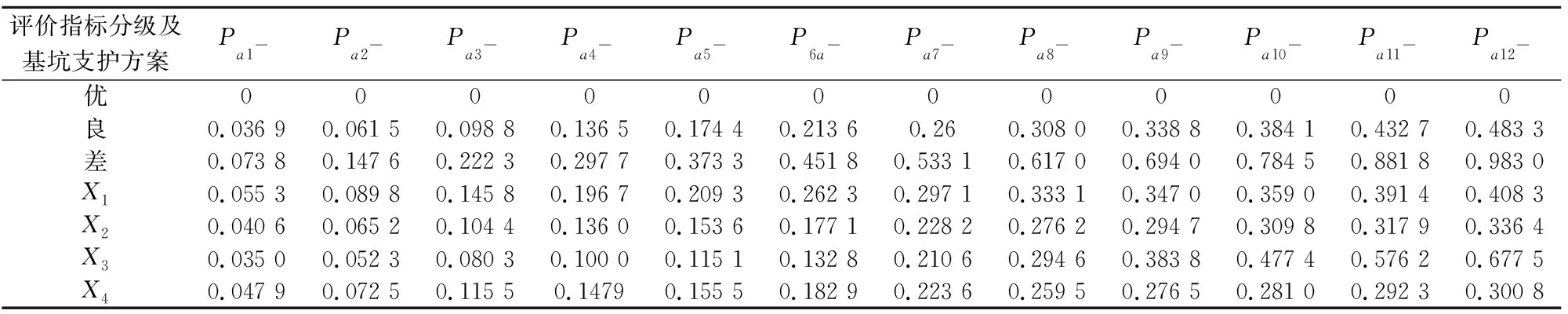
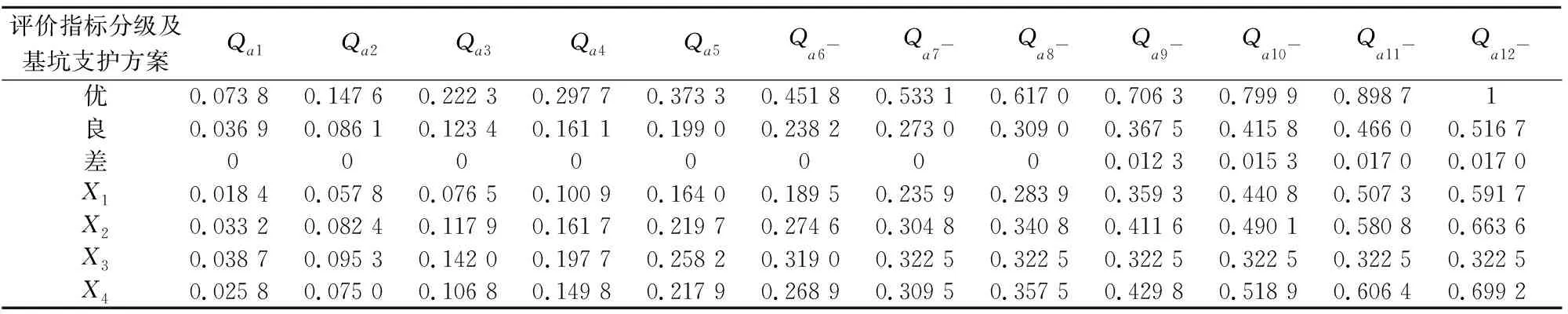
1.3.4 构建对抗决策矩阵
代入指标权值后,得到正、负距离矩阵K+、K-:
(4)
(5)
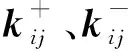
1.3.5 建立比较关系矩阵
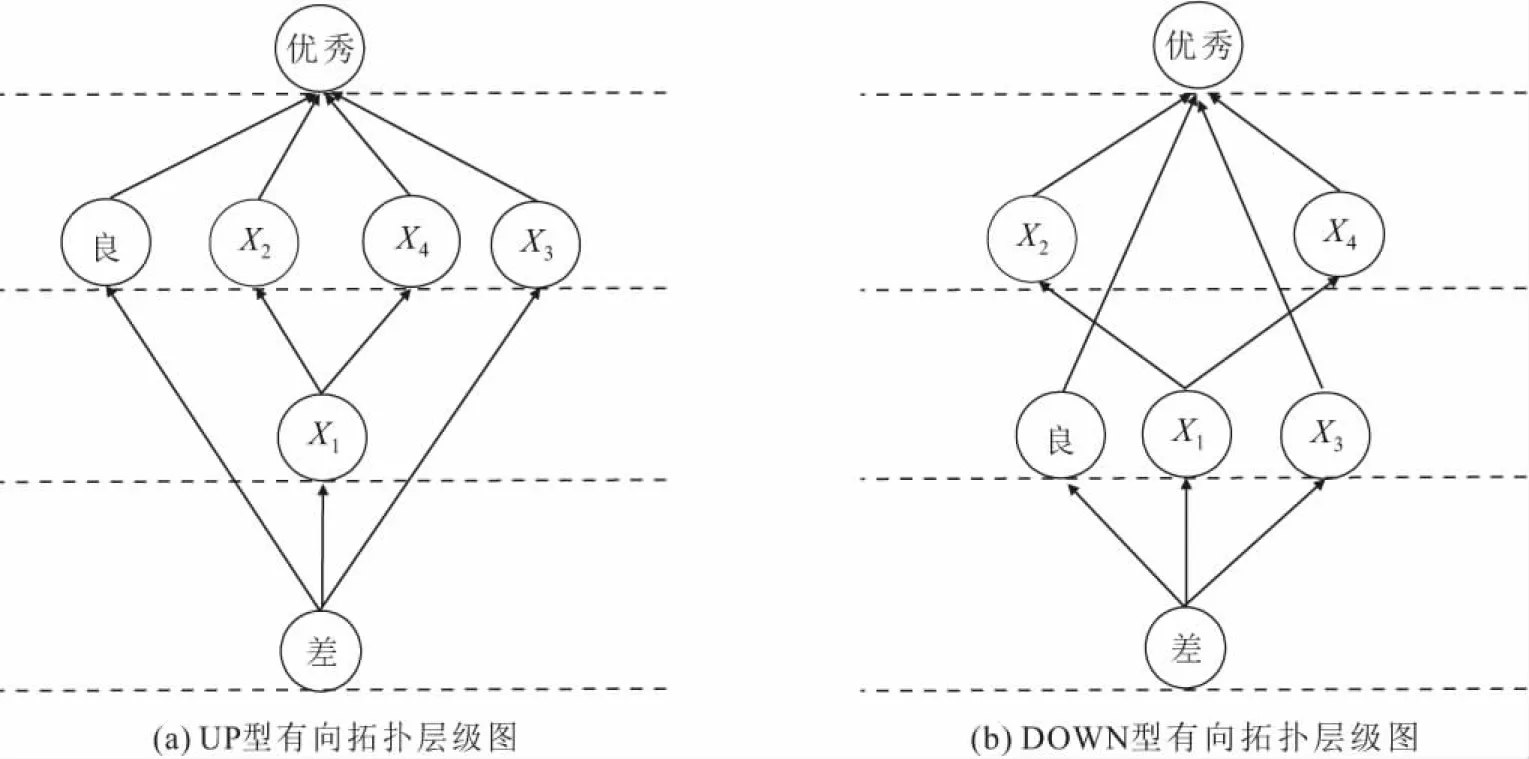
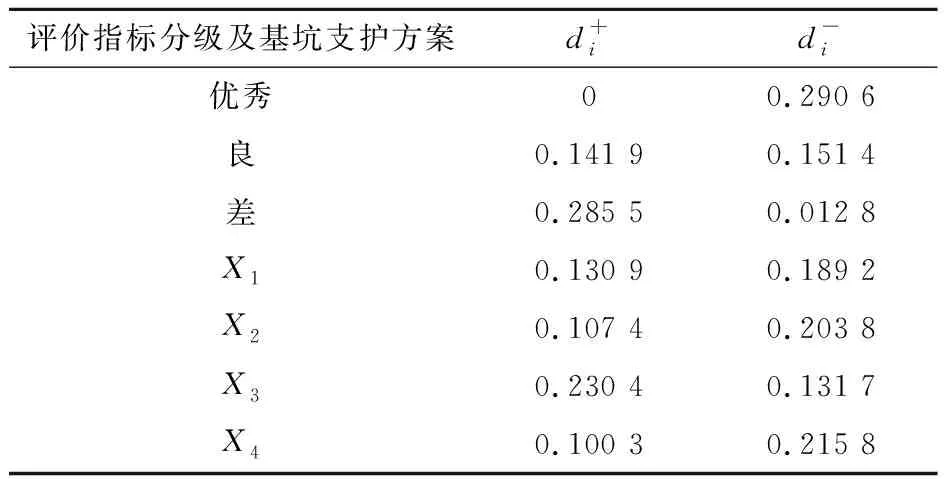
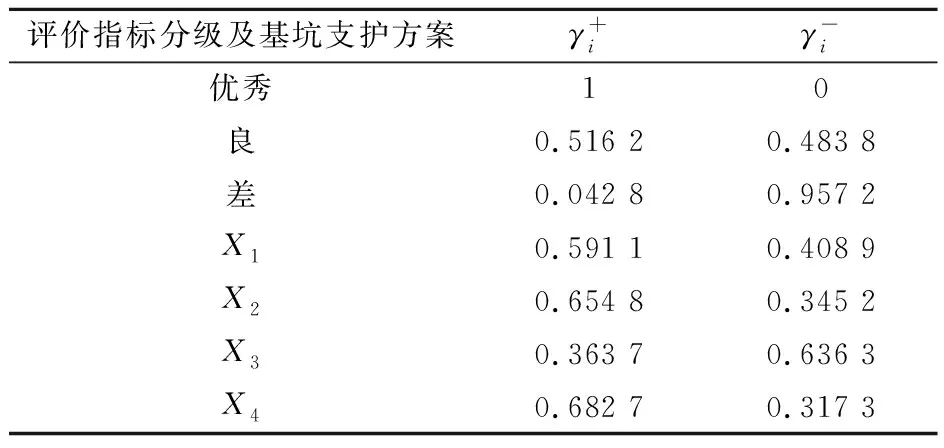
对于对抗决策矩阵中的任意两行(x,y)有px1≥py1,px2≥py2,…,且pxn≥pyn,同时有qx1≤qy1,qx2≤qy2,…,且qxn≤qyn时,记作:x (6) 1.3.6 建立哈斯矩阵 根据相关定义[14-15],比较关系矩阵R即为可达矩阵。该关系矩阵不存在回路,哈斯矩阵求法如下: HS=R-(R-I)2-I (7) 式中:I为单位矩阵;R为可达矩阵;HS为哈斯矩阵。 1.3.7 绘制哈斯图 本文绘制的哈斯图分为UP型层级图和DOWN型层级图。其中,UP型层级图以结果优先的层级划分原则从上往下抽取要素;DOWN型层级图以原因优先的层级划分原则从下往上抽取要素。 UP型层级图和DOWN型层级图属于一组对立型的画法,关系矩阵中的要素即为评价对象,评价对象之间的优劣(好坏,高低)通过有向线段表示,越优的评价对象置于最上层[7,9]。 结果优先的划分准则为T(ei)=R(ei),其原理是将满足条件的结果要素抽取出来放置在顶层,重复该过程直到所有要素均抽取完毕。原因优先的划分准则与结果优先相反,为T(ei)=Q(ei),其原理是将满足条件的原因要素抽取出来放置在底层。其中R(ei)为可达集合,Q(ei)为先行集合,两者的交集为T(ei),即T(ei)=R(ei)∩Q(ei)。其中,ei为关系矩阵要素;R(ei)表示ei的可达集合;Q(ei)表示ei的先行集合;T(ei)表示ei的共同集合。 两种哈斯图解最上层方案取交集,即为理论最优方案。 本文选取武汉市地铁12号线青菱站深基坑工程作为研究对象进行基坑支护方案优选。该地铁车站位于烽胜路与白沙三路交叉口,为地铁12号线与5号线换乘站。车站主体结构外包总长为529.7 m,总宽为22.1 m,基坑深度为17.2~19.6 m;车站北侧依次为龙湖地产地块、清江锦城K1地块、湖北省妇幼保健院地块、换乘楼,车站南侧依次为清江锦城K3地块、加油加气站、清江锦城K4地块。武汉市地铁12号线青菱站与周边地块同步建设,其平面位置如图3所示。该地铁车站基坑开挖深度范围内软弱土层较厚,承压水头高,土层的物理力学性质参数见表1。 表1 某基坑土层的物理力学性质参数 图3 武汉市地铁12号线青菱站深基坑工程平面位置图Fig.3 Location plan of deep foundation pit project at Qingling Station of Metro line 12 in Wuhan City 由于各基坑相互耦合, 在基坑开挖过程中耦合效应可能会使土体变形过大,导致基坑失稳情况出现,因此根据基坑侧壁的岩土工程特性及其周围环境,结合本地区工程经验与现场工程特征并结合专家意见提出了评价指标体系,建立了优、良、差三重客观评价指标以增加评价层次性,如表2所示。其中,X1~X4为待选基坑支护方案,分别为型钢水泥土搅拌桩墙+内支撑(X1)支护方案、钻孔灌注桩+止水帷幕+内支撑(X2)支护方案、内插型钢重力式水泥土挡墙+扶壁(X3)支护方案、地下连续墙+槽壁加固+内支撑(X4)支护方案,以X3为对照方案,参与决策过程以凸显模型科学性;S1~S12为评价指标,分别为施工技术可行性和可靠性、设计计算理论的成熟性、支护系统科学性和先进性、支护结构整体稳定程度、支护结构可承受最大水平变形程度、综合造价(万元)、支护系统允许变形量(mm)、施工对周边基坑的影响、施工对交通的影响、施工工期(d)、施工的难易程度、施工相互干扰程度。 表2 原始决策矩阵 通过公式(1)、(2)对原始数据进行归一化处理,可得到规范化矩阵N=[nij]m×n,见表3。 表3 归一化决策矩阵 通过CRITIC法计算得到各评价指标的权重并进行排序,见表4。 表4 评价指标权重取值及排序 计算正、负距离矩阵K+、K-,并经评价指标权重排序后从左到右进行累加计算,得到对抗决策矩阵Pa、Qa,见表5和表6。 表5 对抗决策矩阵Pa 表6 对抗决策矩阵Qa 通过公式(6),可得到比较关系矩阵,见表7。 表7 比较关系矩阵 通过偏序原则对比较关系矩阵进行抽取,具体抽取过程见表8,并得到UP型与DOWN型哈斯图解,如图4所示。 表8 层级抽取过程 图4 评价指标分级及基坑支护方案哈斯图解Fig.4 Grading of evaluation indicators and Haas diagram of foundation pit support scheme 根据层级抽取过程与比较关系矩阵建立基坑支护方案分级哈斯图解,如图4所示。 由最上层方案取交集可知,基坑支护方案X2、X4为理论最优方案。由于决策矩阵与关系矩阵只依赖指标权重顺序而非大小,使得在实际应用中只需采用合理的定权方法提取指标权重顺序信息即可体现方案间的优劣关系。其中,X3方案在不同的有向拓扑层级图中层级不同,表示该方案具有活动因素特性[17],即在工程应用中的效果无法达到满意预期,因此避免选取具有该特征的类似方案,同时可对判别指标进行优化减少类似因素出现频率,以适应实际需要。此外,由图4可以发现,X2、X4方案之间优劣关系不可取,即无直接路径体现两者之间的优劣,体现了方案排序过程中的模糊性,即理论上总是存在两组不违反前述顺序的指标权重使得两者排序大小不一致。 为了避免实际计算过程中交集元素不唯一,排除同层级干扰直观获取各方案的优劣程度,还应从比较维度上基于评价方案到正、负理想点距离的优劣比较进行逼近,同时计算贴近度从而得到最终的方案排序结果。具体求法如下: (8) (9) 根据公式(8)、(9),可得到距离矩阵和贴近度矩阵,见表9和表10。 表9 距离矩阵 表10 贴近度矩阵 最后由基坑支护方案分级哈斯图解(图4)与贴近度矩阵哈斯图解(图5)共同判定理论基坑支护方案最优解为X4。 本文以武汉市地铁12号线青菱站深基坑工程为依托,建立了TOPSIS-AISM夹逼对抗解释结构模型,并将该模型运用于基坑支护方案优选中,通过对决策矩阵与评价指标体系进行分析,以验证该模型的合理性与科学性,得到的主要结论如下: 1) 本文将TOPSIS法与AISM法相结合,通过建立哈斯图解的方式对各基坑支护待选方案进行分层优选,在展现各方案层级关系的同时体现了方案排序中的模糊性,相较传统TOPSIS法其对各待选方案在具体工程项目中的优劣性表现更加科学全面。 2) 该模型对指标赋权方法适应性更强,在实际应用过程中只需提取指标权重顺序信息即可得到科学合理的结果,相比传统TOPSIS法其更具排序稳定性。 3) 该模型不依赖数据矩阵确定正、负理想点,相较传统TOPSIS法其评价标准更加具有客观性与普遍性。 4) 该模型可甄别活动性因素,使工程人员避免选取具有该特征的类似方案,相较传统TOPSIS法其工程指导性更强。2 工程实例分析
2.1 工程概况

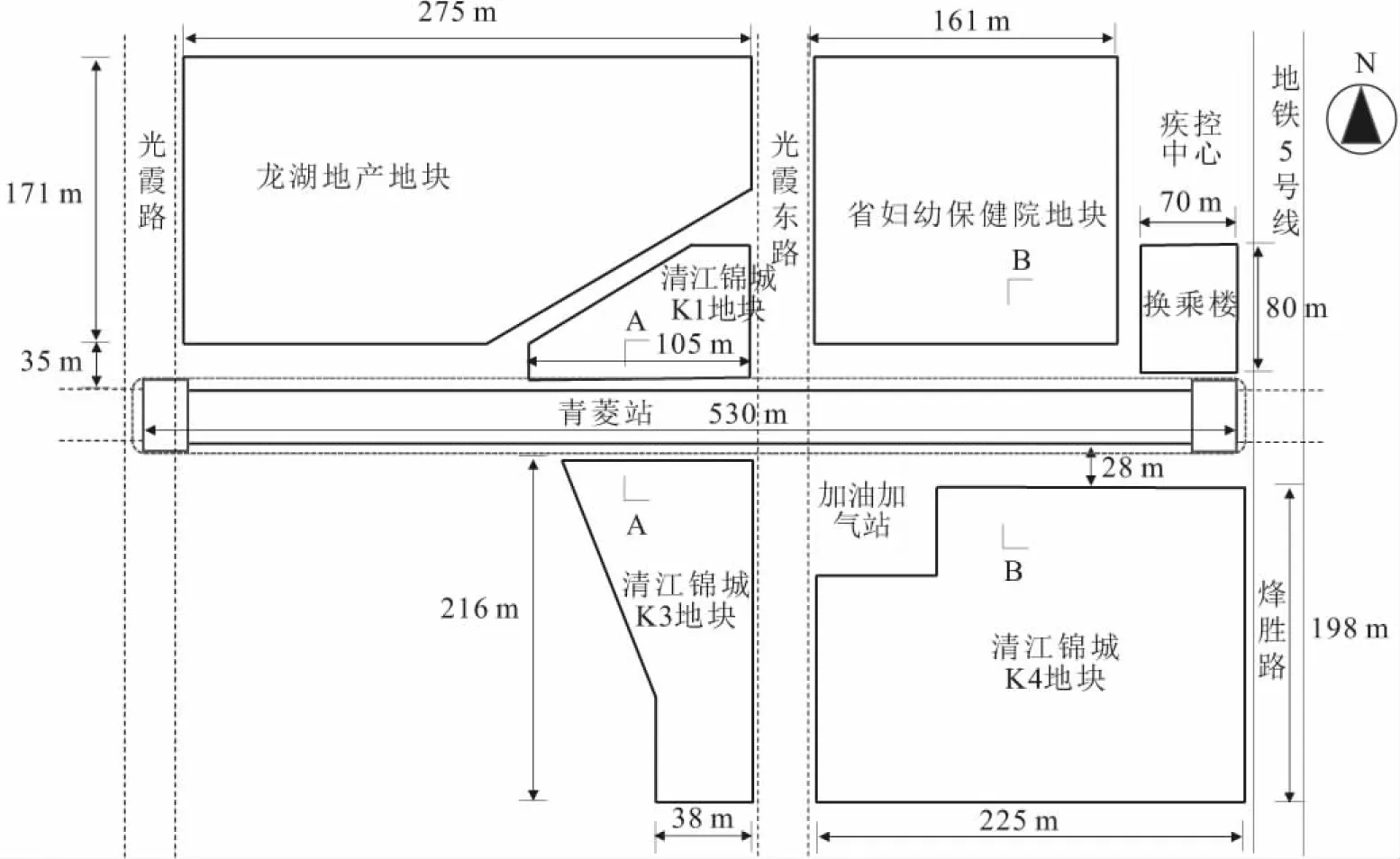
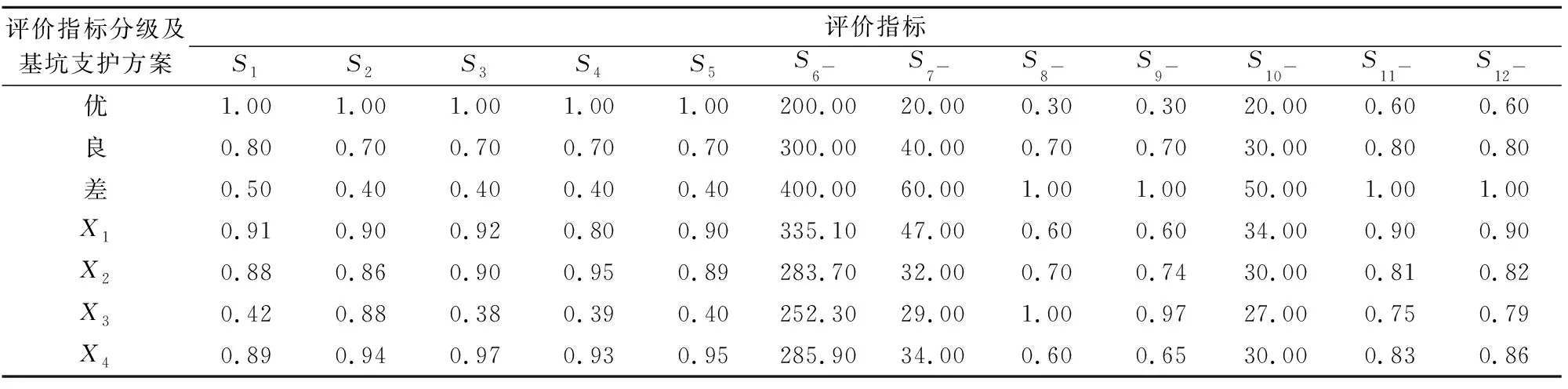
2.2 数据处理

2.3 指标权重计算
2.4 构建对抗决策矩阵
2.5 构建比较关系矩阵

2.6 绘制哈斯图

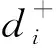
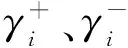
3 结 论

