基于应变软化模型的地下储气库井筒水泥环完整性研究
冯膑辉,姜婷婷,尚修瑞,张建华
(1.武汉理工大学安全科学与应急管理学院,湖北 武汉 430070;2.武汉理工大学资源与环境工程学院,湖北 武汉 430070)
天然气作为一种清洁能源,在工业生产、交通运输和生活起居等领域均有广泛的应用。根据国家发改委和国家能源局印发的《“十四五”现代能源体系规划》,到2025年,全国集约化布局的储存天然气能力达到550亿m3至600亿m3,对于我国天然气行业而言,“十四五”的主要任务之一是加快地下储气库建设[1]。地下储气库具有储气规模大、成本低的优点,是我国储备天然气首选方式[2]。地下储气库可靠运行的重要前提之一是井筒密封特性良好。因此,保证井筒在不同工况下的密封性,尤其是保证井筒水泥环的完整性对于保障地下储气库平稳运行具有重要意义[3]。
对于地下储气库井筒水泥环完整性失效问题,国内外学者开展了一系列研究。如:Zinkhan等[4]提出地下储气库井筒由套管-水泥环-地层构成;Vrlstad等[5]、舒刚等[6]基于储气库注采井水泥环试验设备,对储气库注采井水泥环破坏机理与影响因素进行了研究;殷有泉等[7]、赵新波等[8]基于弹性力学,将井筒问题简化为平面问题给出了非均匀地应力和热固耦合下套管-水泥环-井筒组合体应力场的解析解;赵效锋等[9]基于弹塑性力学,将井筒问题简化为多层组合厚壁筒问题,得出了固井界面微环隙的计算方法。数值模拟方法由于其试验条件可控且具有便于进行重复试验的优势,在地下储气库井筒稳定性研究中得到了广泛应用,如:Valov等[10]采用完全耦合的线性热-孔隙-弹性模型,描述了流体压力和非均质地应力对套管的压缩作用,并基于有限元方法研究了导致地下储气库井筒水泥环失效的因素;Yuan等[11]通过建立三维地层-水泥环-套管弹性组合模型,研究了不同作业参数对两胶结面的范式等效应力和组合体总位移的影响;Bu等[12]针对套管-水泥-地层界面易产生微环隙问题,基于ABAQUS有限元软件研究了套管内压降低过程中水泥与套管界面的拉应力,以及水泥硬化收缩过程中水泥与地层界面的拉应力。
以上关于地下储气库井筒水泥环完整性的研究中,水泥环本构模型为线弹性或理想弹塑性,然而水泥环在围压作用下发生破坏存在塑性形变[13],且有应变软化现象[14],故在地下储气库井筒完整性研究中运用能反映水泥环破坏全过程的水泥环本构模型对于井筒水泥环密封失效机理研究具有重要的意义。本文基于水泥环力学行为特性,考虑水泥环在围压条件受载时的应变软化特征,建立了水泥环应变软化本构模型,并通过建立套管-水泥环-地层组合体数值模型,根据地下储气库作业特点,对地下储气库井筒水泥环密封失效原因进行了分析,验证了所建立的水泥环本构模型的可靠性。
1 考虑峰前硬化阶段的岩石应变软化模型建立
1.1 典型岩石应力-应变曲线
相较于金属材料,岩石材料内部结构复杂,并且由于不同岩石材料之间存在性质差异,因此岩石材料的力学行为也各不相同。前人研究岩石性质对工程产生的影响时,常将岩石应力-应变曲线简化为理想弹塑性、理想弹脆性和理想应变软化3种形式,如图1所示。图1(a)中,对于理想弹塑性材料,在弹性阶段,材料应力与应变呈线性变化,在塑性阶段,材料应力保持不变,而材料应变随时间推移逐渐增大;图1(b)中,对于理想弹脆性材料,材料应力达峰值之后迅速跌落,随后材料进入塑性流动阶段;图1(c)中,对于理想应变软化材料,与弹脆性材料相比,材料在应力达峰值之后有一个应变软化阶段,随后再进入残余阶段。
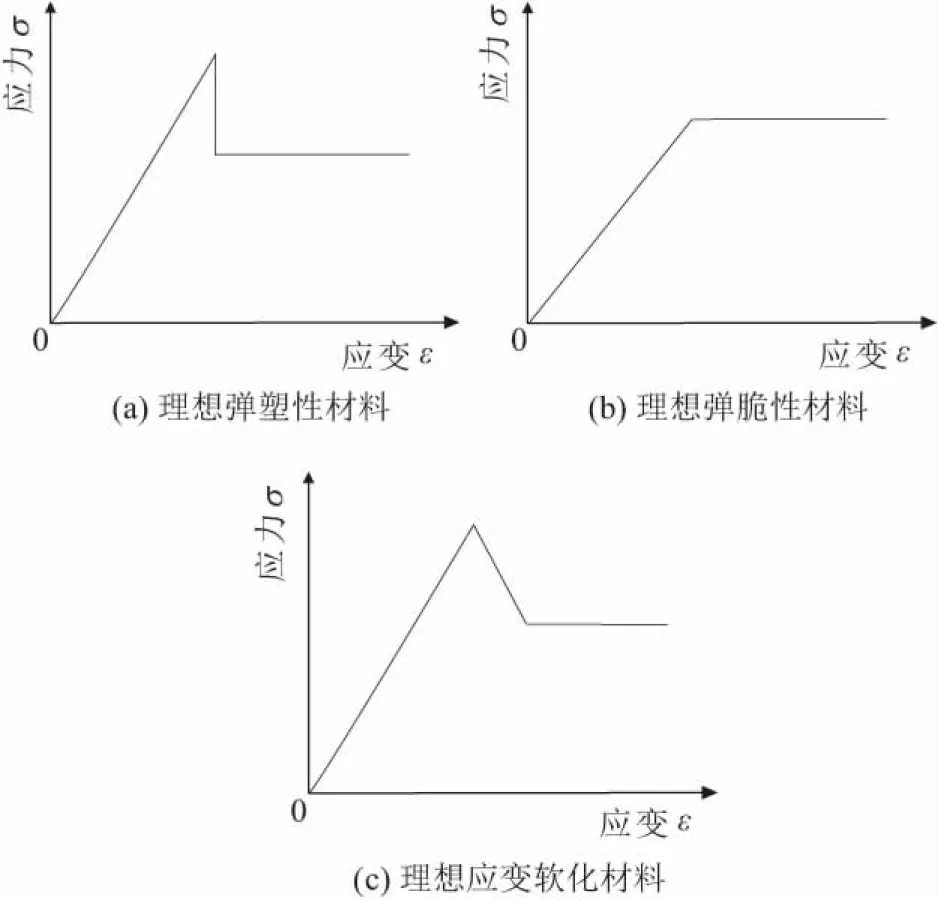
图1 典型的岩石应力-应变曲线[15]Fig.1 Typical simplified rock stress-strain curves[15]
以上简化的岩石应力-应变曲线尽管应用广泛,但也存在不合理之处,即未考虑材料的峰前硬化阶段的力学行为。如图2所示,以典型的岩石全应力-应变曲线为例[16],该典型的岩石全应力-应变曲线一般划分为5个阶段:①OA段,岩石内部微裂隙初始受压闭合阶段;②AB段,岩石线弹性变形阶段;③BC段,岩石应变软化阶段;④CD段,岩石应力迅速跌落阶段;⑤DE段,岩石残余应力阶段。因此,为了更为恰当地表达岩石的力学行为,应当准确描述岩石应力出现拐点前后即应变软化阶段的岩石应力-应变曲线情况。
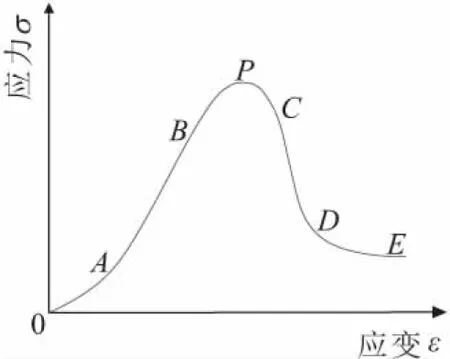
图2 典型的岩石全应力-应变曲线Fig.2 Typical complete stress-strain curve of rocks
1.2 水泥环应变软化模型建立
假设水泥环在初始屈服后应力状态均符合莫尔-库仑强度准则,即:
(1)
式中:σ1和σ3分别为水泥环最大和最小主应力(MPa);c和φ分别为水泥环的黏聚力(MPa)和内摩擦角(°)。
用轴向塑性应变εp作为软化参数,在水泥环出现屈服后,将其应力看作轴向应变ε的函数,水泥环软化阶段应力-应变关系函数可表示如下[17]:
(2)
其中:
(3)
式中:ε为水泥环轴向应变。
如图3所示,将水泥环黏聚力与软化参数之间的函数关系根据岩石应力-应变曲线划分为多段并进行分析,以描述水泥环黏聚力的演化规律。
对于水泥环初始屈服至强度峰值软化阶段任意微元段,有:
E0(dε-dεp)=Δσ=σ′(ε)dε
(4)
式中:E0为水泥环初始屈服前的弹性模量(MPa);σ′(ε)为在轴向应变ε处水泥环的应力-应变曲线的斜率。
水泥环初始屈服前的弹性模量E0可用初始屈服点与原点连线的斜率来表示:
(5)
式中:σ0为水泥环初始屈服强度(MPa);ε0为水泥环初始屈服强度处对应的轴向应变。
因此,对于峰前应变硬化阶段,三轴压缩过程中水泥环轴向应变ε1与轴向塑性应变εp之间的关系可表示为
(6)
同理,对于峰后应变软化阶段,有:
(7)
将岩石应力-应变全过程曲线划分为4阶段,如图4所示。
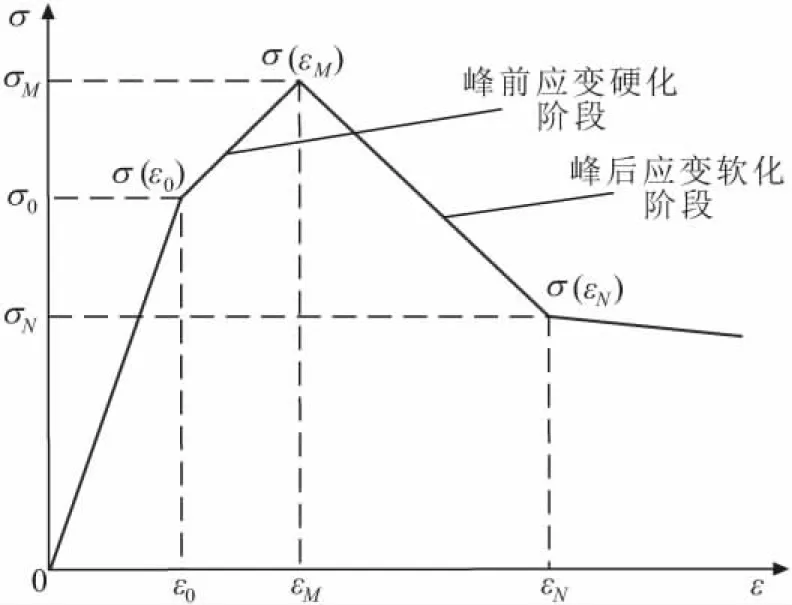
图4 4阶段岩石应变软化模型[18]Fig.4 4-stage strain softening model of rock[18]
对于图4中表达的岩石应变软化模型,峰前应变硬化阶段岩石应力-应变曲线关系式为
(8)
式中:σM、σ0分别为水泥环峰值强度和初始屈服强度(MPa);εM、ε0分别为水泥环峰值强度和初始屈服强度处对应的轴向应变。
联立上式,可得峰前应变硬化阶段水泥环黏聚力的演化规律为
(9)
式中:η为软化参数。
同理,可得峰后应变软化阶段水泥环黏聚力的演化规律为
(10)
由上两式可知:水泥环应力-应变曲线呈线性阶段时,水泥环黏聚力便与软化参数呈线性变化,而水泥环应力-应变曲线呈非线性阶段时,可将其处理为若干直线段联合以代替该曲线。
2 模型验证
2.1 模型计算参数确定
为了证明本文所建立的考虑峰前硬化阶段岩石应变软化模型的合理性,需要基于岩石强度参数的演化规律,对岩石应力-应变全过程曲线通过数值模拟试验进行验证。文献[19]给出了水泥环三轴压缩试验资料,包括水泥环的弹性模量、泊松比以及不同围压下三轴压缩应力-应变曲线,并对三轴压缩试验曲线进行简化,见图5。
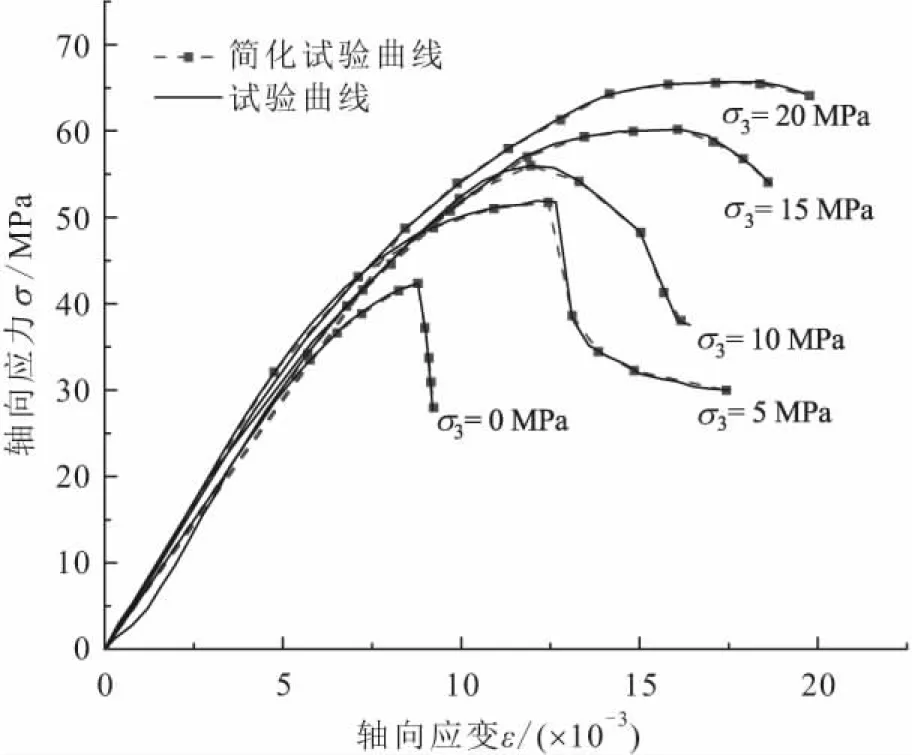
图5 不同围压下水泥环三轴压缩试验应力-应变曲线Fig.5 Stress-strain curves of the triaxial compression test of the cement ring under different confining pressures
设简化试验曲线每一构成部分的两端点坐标分别为(ε′,σ′)、(ε″,σ″),且初始屈服点坐标为(ε0,σ0)。由式(5)计算得到不同围压下水泥环初始屈服前的弹性模量E0,见表1。
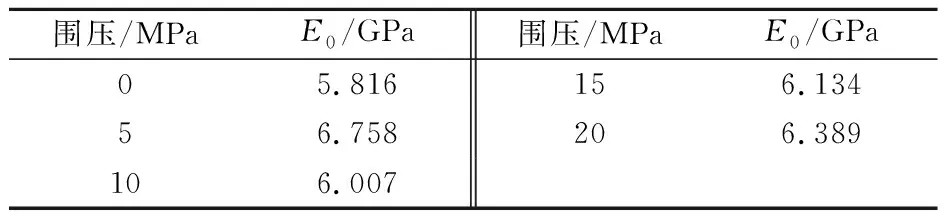
表1 不同围压下水泥环初始屈服前的弹性模量E0
对于水泥环初始屈服至峰前硬化阶段,由式(6)计算得到水泥环轴向塑性应变εp,并由下式计算软化参数η:
(11)
式中:ε″和ε′分别为简化的各段水泥环应力-应变曲线结束时和开始时的轴向应变;σ″和σ′分别为简化的各段水泥环应力-应变曲线结束时和开始时的轴向应力(MPa);η为软化参数。
由式(2)计算得到峰前硬化阶段水泥环的黏聚力值。
同理,可计算出峰后软化阶段水泥环的黏聚力。将上述计算结果汇总于表2。
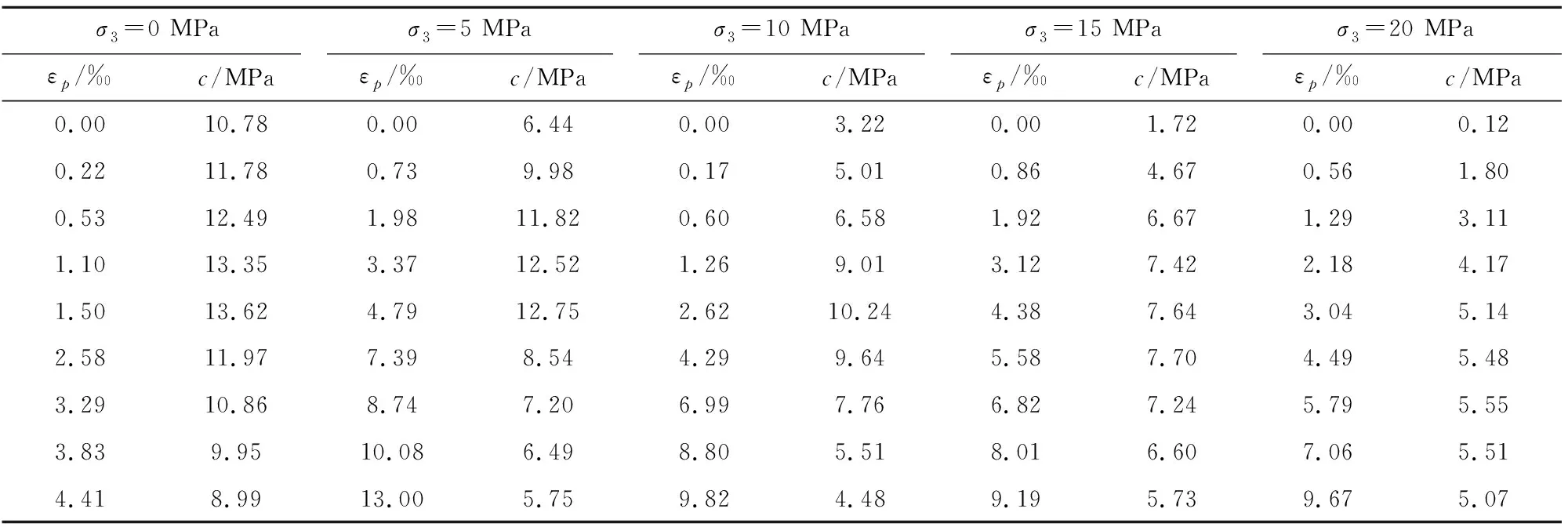
表2 不同围压和软化状态下水泥环的黏聚力值
2.2 水泥环试样三轴压缩数值模拟
本文利用FLAC3D软件建立了标准圆柱体水泥环试样数值模型(直径为50 mm,高为100 mm),模型材料密度为1 900 kg/m3,弹性模量为5.99 GPa,泊松比为0.20,内聚力为5.30 MPa,内摩擦角为24.5°,抗拉强度为3.61 MPa,对圆柱形网格模型顶、底面用位移控制轴向加载,侧面施加垂直压应力以模拟围压,所建立的数值模型如图6所示。结合表2中的数据,利用建立的水泥环应变软化模型,对围压分别为0、5、10、15和20 MPa条件下的水泥环试样进行了三轴压缩数值模拟,并将水泥环三轴压缩试验应力-应变曲线与数值模拟曲线进行了对比,其结果见图7。

图6 标准圆柱体水泥环试样FLAC3D数值模型示意图Fig.6 Schematic diagram of FLAC3D numerical model for standard cylindrical cement ring sample
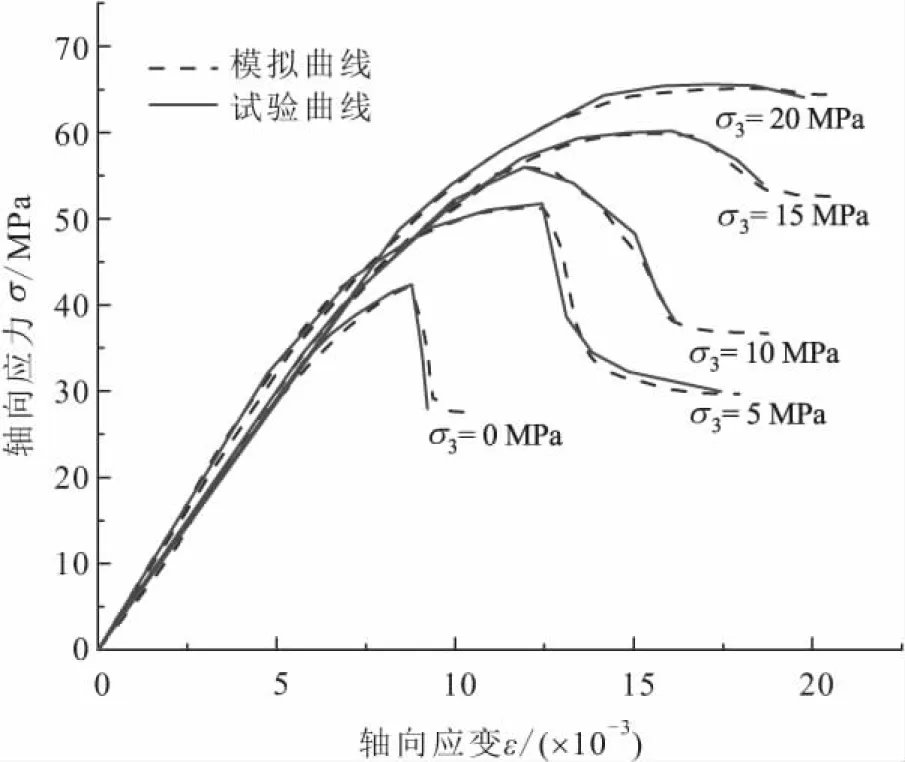
图7 不同围压下水泥环三轴压缩试验应力-应变曲线 与数值模拟曲线的对比Fig.7 Comparison between stress-strain curves of cement ring triaxial compression test and numerical simula- tion curves under different confining pressures
由图7可知:采用水泥环应变软化模型计算得到的水泥环应力-应变模拟曲线经历了弹性变形阶段、峰前硬化阶段、峰后软化阶段和残余阶段,随着围压的增大,水泥环峰值强度不断增加,模拟曲线变化趋势与试验曲线基本一致;模拟曲线弹性阶段在初始屈服点结束,初始屈服点与原点连线的斜率对应于水泥环发生屈服前的弹性模量,这与本文假设相符;此外,对于低围压下水泥环应力-应变曲线,至峰值强度后,水泥环应力跌落,以残余强度维持一定形态,而在高围压下水泥环应力-应变曲线经历了峰值强度,也不会出现急剧的应力跌落现象,而是表现为延性,其强度缓慢降低。
文献[20]指出边坡岩土体剪应变增量最大处相对于其他位置最容易发生破坏变形。因此,可以通过岩石最大剪应变增量的变化情况来判断模型对应力作用的敏感程度。为了确定围压对水泥环试样破坏程度的影响,采用莫尔-库仑本构模型和应变软化本构模型,经相同的位移加载计算得到的试样最大剪应变增量变化曲线,如图8所示。

图8 不同围压下水泥环试样内部各点最大剪应变增量变化曲线Fig.8 Curves of maximum shear strain increment at each point inside the cement ring sample under different confining pressures
由图8可知:采用应变软化模型计算得到的水泥环试样最大剪应变增量均大于采用莫尔-库仑模型计算值,这是因为采用应变软化模型时,水泥环试样对应力作用更敏感,更易发生破坏;通过对比两组曲线的峰值发现,在同等的加载条件下,采用两种本构模型计算得到的水泥环试样最大剪应变增量的差值随围压的增加而减少,这主要是由于采用应变软化模型时水泥环试样产生的最大剪应变增量减小,并在围压的作用下,水泥环试样的强度弱化速度减慢,抵抗变形的能力增强。由此可见,对地下储气库井筒水泥环完整性进行评价采用应变软化模型更为合适。
3 地下储气库井筒水泥环完整性分析
3.1 数值模型建立
本研究先使用ANSYS软件建立地下储气库井筒模型并进行网格划分,模型长、宽和高分别为1 m、1 m和0.05 m,模型单元为60 420个、节点为73 338个;然后将所建立的地下储气库井筒模型通过软件接口导入FLAC3D软件中,生成FLAC3D井筒网格模型,如图9(a)所示,其中内部第一个圆环表示套管,最外层表示地层,套管与地层之间的圆环部分为水泥环。对构成井筒的套管赋予线弹性模型,地层设为泥岩且采用莫尔-库仑模型[21],并分别采用莫尔-库仑模型和应变软化模型对水泥环的最大剪应变增量、最大主应力和内部位移进行了模拟计算与分析,模型材料参数见表3。水泥环与套管和井筒之间的接触面采用FLAC3D软件提供的分界面单元模拟[22],分界面刚度10倍于周边单元体的最大等效刚度,其计算公式如下:

表3 模型材料参数
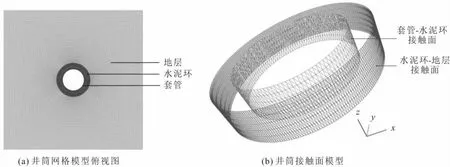
图9 地下储气库井筒网格模型示意图Fig.9 Wellbore grid model of underground gas storage
(12)
式中:Kn为分界面法向刚度(GPa);Ks为分界面切向刚度(GPa);K为体积模量(GPa);G为剪切模量(GPa);ΔZmin为法向上与分界面单元体相接触的网格最小宽度(m)。
套管-水泥环和水泥环-地层的接触面参数见表4,所建立的井筒接触面模型见图9(b)。

表4 水泥环接触面参数
模型边界条件设置如下:
1) 套管、水泥环、地层的下表面及地层四周固定三向位移。
2) 根据上覆岩层的平均容重和深度,对前后左右四个面分别施加20 MPa的垂直应力以代表水平地应力,对顶面施加21 MPa的垂直应力代表上覆岩层重力[19]。
3) 对套管内表面施加一个通过FISH函数添加的使用正弦函数作为返回值的呈周期变化的法向应力来作为套管循环载荷。
在模拟计算时,首先考虑到岩层自重应力的影响,进行初始地应力的平衡;然后用空模型开挖出井筒;最后计算在套管内压循环荷载作用下,水泥环位移、应力场的变化。
在地下储气库注采循环作业中,井筒内部会受到交替的高压和低压作用。在注气阶段,水泥环受到的应力增大并且产生变形;而在采气阶段,水泥环受到的应力减小但仅有弹性变形恢复,即水泥环经加载后再卸载有塑性变形存在[23],并且在持续交替压力下,水泥环累积塑性变形不断增加。因此,水泥环最大剪应变增量、最大主应力和径向位移会随地下盐穴储气库注采作业次数发生变化,其中:
1) 最大剪应变增量集中处反映水泥环发生剪切破坏的可能位置,FLAC3D软件中定义应变增量张量是与节点位移相关的物理量,在一个无限小的时间dt内,单元应变增量计算公式为[20]
(13)
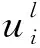
2) FLAC3D软件中正值表示拉应力,最大主应力反映水泥环受拉情况,单元最大主应力计算公式为[22]
(14)
式中:J2为偏应力张量第二不变量;θσ为应力洛德角(°);σm为平均应力(MPa)。
3) 水泥环径向位移反映水泥环内部发生形变的程度,为水泥环径向各点在受力产生形变后所在位置与原始位置坐标点的差值。
3.2 模拟计算结果与分析
地下盐穴储气库寿命一般为30~50年[24],为了衡量地下储气库整个寿命周期内井筒水泥环的完整性,将井筒注采气次数设为15、30、45和60次。
3.2.1 水泥环最大剪应变增量分析
本研究分别采用莫尔-库仑本构模型和应变软化本构模型模拟计算得到不同井筒注采气次数下水泥环的最大剪应变增量云图,见图10和图11所示。
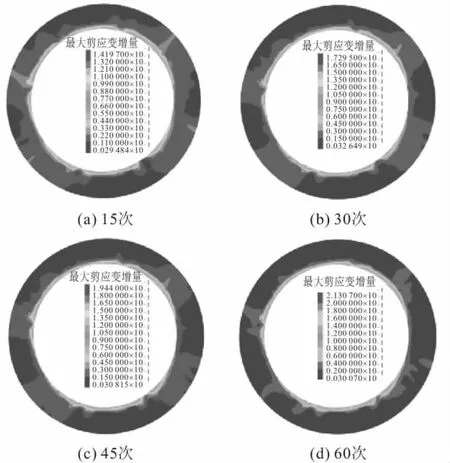
图10 不同井筒注采气次数下水泥环最大剪应变增量 云图(莫尔-库仑本构模型)Fig.10 Contour of maximum shear strain increment of cement sheath under different gas injection and production times (Mohr-Coulomb constitutive model)

图11 不同井筒注采气次数下水泥环最大剪应变增量 云图(应变软化本构模型)Fig.11 Contour of maximum shear strain increment of cement sheath under different gas injection and production times (strain softening constitutive model)
由图10和图11可知:
1) 随着注采次数的增加,水泥环内侧发生的最大剪应变增量呈增加趋势。
2) 井筒注采次数相同时,采用莫尔-库仑本构模型模拟计算得到的水泥环最大剪应变增量小于采用应变软化本构模型的计算值;在经历15次注采循环后,采用上述两种本构模型计算得到的水泥环最大剪应变增量分别为0.146和0.194;在经历60次注采循环后,采用上述两种本构模型计算得到的水泥环最大剪应变增量分别为0.217和0.263。
3.2.2 水泥环最大主应力分析
本研究采用莫尔-库仑本构模型和应变软化本构模型计算得到的不同注采气次数下水泥环模拟最大主应力云图,见图12和图13。
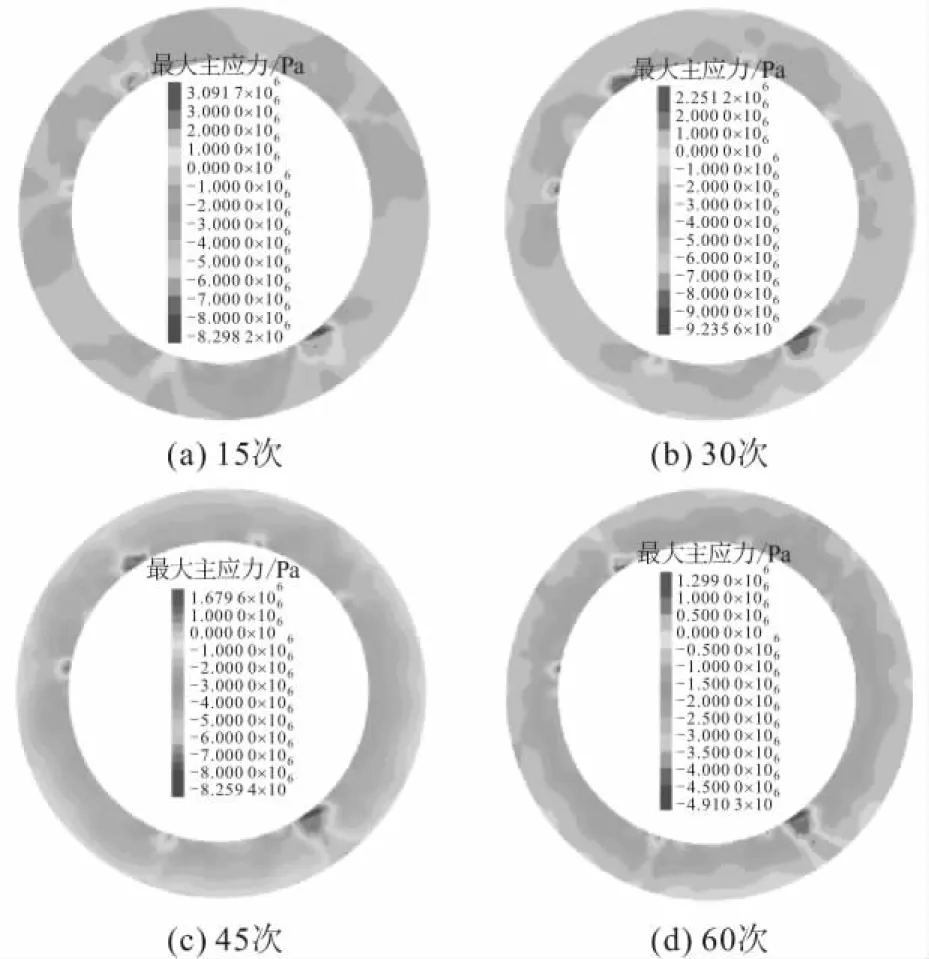
图12 不同井筒注采气次数下水泥环最大主应力云图 (莫尔-库仑本构模型)Fig.12 Contour of maximum principal stress of cement sheath under different gas injection and production times (Mohr-Coulomb constitutive model)
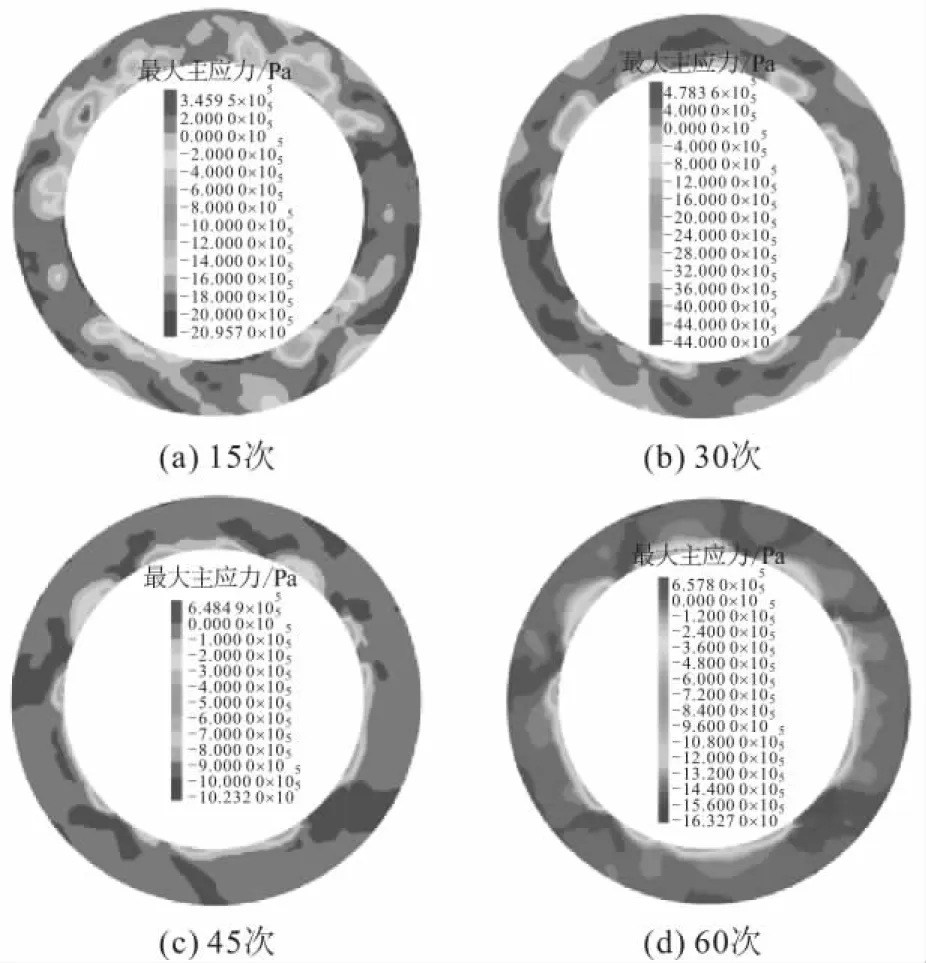
图13 不同井筒注采气次数下水泥环最大主应力云图 (应变软化本构模型)Fig.13 Contour of maximum principal stress of cement sheath under different gas injection and production times (strain softening constitutive model)
由图12和图13可知:
1) 对于两种本构模型的计算结果,最大主应力的最大值位置均在水泥环内侧,且均为压应力。
2) 水泥环内侧有拉应力集中现象,拉应力集中区域主要呈两点分布且随着循环加卸载次数的增加而扩大,但均小于水泥环的抗拉强度(图12),即此时水泥环不会出现径向裂隙。
3) 最大主应力集中区域呈多点状均匀分布在水泥环内侧,随着循环加卸载次数的增加,该区域逐渐扩大并有连结成环的趋势,且有最大主应力集中区域的应力值大于水泥环的抗拉强度(图13),对于井筒则会出现套管-水泥环分离现象,进而使水泥环密封失效。
3.2.3 水泥环径向水平位移分析
在完成30次注采气循环后,水泥环径向不同位置处的水平位移图,见图14。
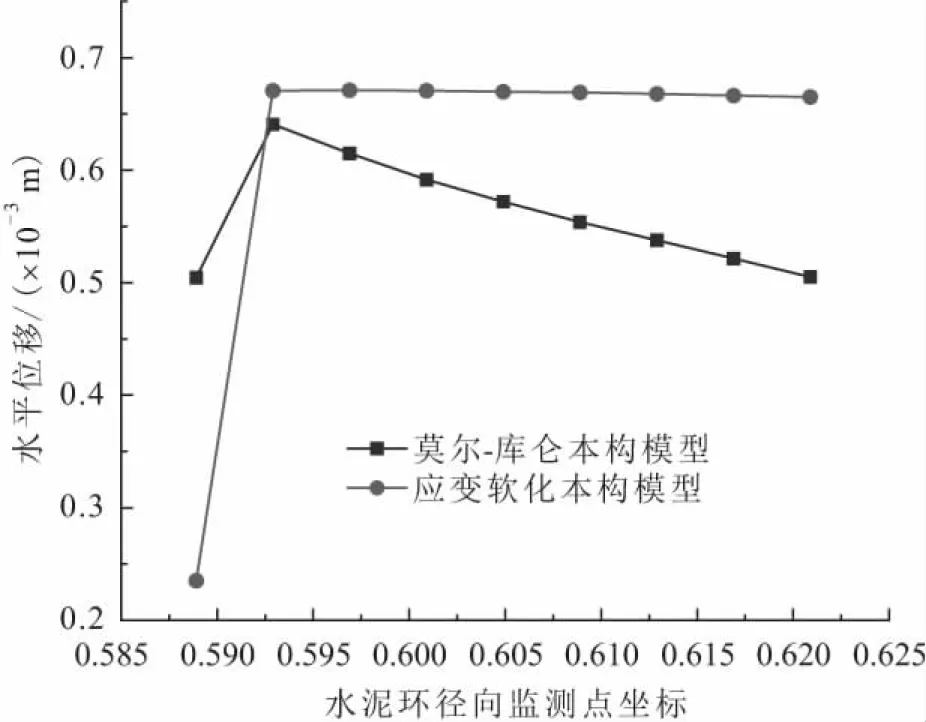
图14 水泥环径向不同位置处的水平位移Fig.14 Radial horizontal displacement of cement sheath
由图14可以看出:在同等条件下,采用应变软化本构模型计算得到的水泥环径向水平位移普遍大于采用莫尔-库仑本构模型的计算值,且采用应变软化本构模型计算得到的水泥环径向水平位移在增加至峰值后维持在一定水平,其变化细微,而采用莫尔-库仑本构模型计算得到的水泥环径向水平位移增加至峰值后逐渐减小;此外,首个水泥环径向监测点位于套管与水泥环交界面,该监测点与其邻近监测点水泥环径向水平位移差值明显大于其他相邻监测点差值。
4 结 论
1) 本文基于莫尔-库仑强度准则,考虑峰前硬化阶段和峰后软化阶段对水泥环应变软化的影响,选取轴向塑性应变为软化参数,获取了水泥环黏聚力随轴向塑性应变的变化规律,以此建立了水泥环应变软化本构模型,模拟结果表明:运用该模型模拟得到的水泥环应力-应变曲线与试验曲线一致程度较高,能准确描述水泥环峰前硬化阶段和峰后软化阶段的力学行为。
2) 对水泥环试样发生最大剪应力增量的分析结果表明:水泥环的抗压强度受围压的影响,相比于莫尔-库仑本构模型,应变软化本构模型更能表达出水泥环的强度参数随应力增加而发生软化的特性。
3) 建立了套管-水泥环-地层组合体数值模型,对水泥环赋予莫尔-库仑本构模型和应变软化本构模型,模拟分析了地下储气库井筒水泥环的完整性,结果表明:相比于采用莫尔-库仑本构模型的计算结果,采用应变软化本构模型时,水泥环内部产生的径向水平位移较大,水泥环所受的应力也更大,此时水泥环更易发生塑性变形,产生微环隙。

