基于模型融合的装饰过程造价预测研究
孙传志
(大连财经学院 管理学院,辽宁 大连116000)
近年来,随着信息科学技术的不断发展,建筑工程行业也逐渐走上信息化的道路,模型融合、岭回归、随机森林以及XGBoost等算法在工程造价领域被广泛应用[1]。社会经济的发展加快了建筑工程行业的进步,也对建筑有了更多的要求,人们除了关注建筑的实用性、观赏性以及经济性之外,还越来越关注建筑装饰过程的工程质量[2]。造价预测对于每个装饰工程来说都是必不可少的流程,是装饰工程项目前期准备阶段的首要任务[3]。传统的预测方式具有耗时长、内容复杂以及收集数据量庞大等局限性,使得企业难以在短时间内获得准确的造价预测分析结果[4]。在装饰工程项目的前期准备阶段,如果未得到准确的造价预测结果,那么在项目实施阶段就很难进行成本的控制。集成学习是由多个学习模型构建组合成的一个学习模型,该模型集合了多个学习模型的优势,因此,在机器学习领域中备受关注。单一的预测模型因其算法自身的理论差异,无法满足实际工程造价预测的精度和效率要求。模型融合算法可以很好地平衡各个算法之间的性能,在充分发挥各算法优势的同时避免各算法的不足[5]。在这一背景下,本文研究基于模型融合的装饰过程造价预测模型,以期为得到更高的造价预测效率和精度提供参考。
一、基于模型融合的装饰过程造价预测模型
(一)基于优化Stacking算法的模型融合
模型融合算法不是指具体的某一个算法,而是将多个弱模型融合为一个强模型的算法,因此也被称为集成学习[6]。模型融合算法包含了Stacking堆叠法、平均法、排序法、Blending混合法和投票法等四种类型,其中Stacking堆叠法是相对高级的模型融合法[7]。Stacking堆叠法是在原始数据的基础上构建多层模型并用来训练出多个基学习器,再将基于学习器的预测结果进行拟合预测,从而训练出新的学习器[8]。Stacking算法分为单层Stacking和多层Stacking。单层Stacking是最为常见的Stacking结构,是指在基学习器上只堆叠了一层元学习器,而多层Stacking是指堆叠了两层及以上的元学习器。Stacking算法的集成学习原理如图1所示。
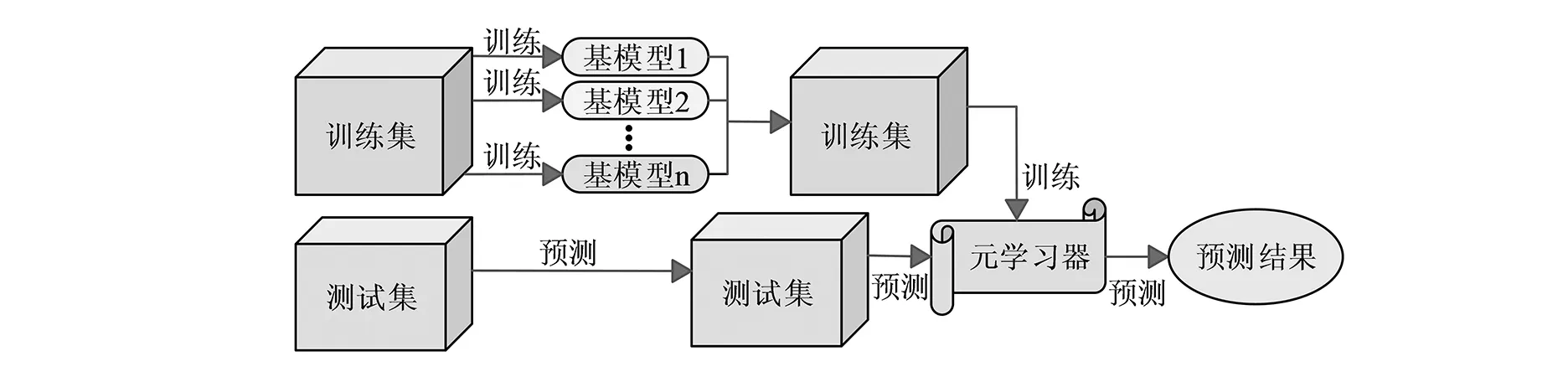
图1 Stacking算法的集成学习原理
由图1可以看出,Stacking算法的集成学习原理框架分为两层,第一层是由多个基模型学习器组成,第二层是由元学习器组成[9]。(1)将数据集分为训练集和测试集,将部分训练集的数据输入到基模型中进行训练,训练后的基模型分别在剩下的训练集和测试集上再次进行预测和训练,从而分别得到预测和测试标签;(2)进入第二层元学习器中再次进行训练并预测,得出预测结果。数据集的表达式如式1所示。
D={(yn,xn),n=1,2,...,N}
(式1)
式1中,D表示数据集,N表示样本总数量,yn表示第n个样本经过训练后的输出值,xn表示第n个样本的特征向量。将数据集等分为M个子集,设置第一层的基学习器数量为K,那么,学习器Lk的取值范围为[1,2,3,...,K]。使用第m个算法对训练集进行建模,得到的新数据集如式2所示。
Dnew={(yn,z1n,...,zmn),n=1,2,...,N}
(式2)
式2中,zmn表示学习器Lk对该测试集的预测值,第二层元学习器Lnew使用线性算法作为训练模型,能够减少第一层输出结果的误差,从而提升模型精度。Stacking算法性能易受到学习器和属性的影响,虽然Stacking算法具有输出结果以概率分布的优点,但算法也存在运行时间长、分类性能不高等缺点。为了提高Stacking算法的性能,可以在该算法的基础上降低特征维数并增加一层初级层进行优化。单层Stacking算法只包含两层,即由多个学习器组成的初级学习层和元学习层,优化后的Stacking算法属于多层Stacking,包含了两层初级学习层和一层元学习层。第二层学习器的训练集如式3所示。
(式3)
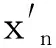
H(x1,x2)=‖P(x1)-P(x2)‖2
(式4)
式4中,P(x1)和P(x2)都表示元学习层中的输入向量,当基分类器的数量增加时用T′表示,此时输入向量之间的欧式距离如式5所示。
H′(x1,x2)=‖P′(x1)-P′(x2)‖2
(式5)
式5中,H′(x1,x2)>H(x1,x2),可以看出,随着基分类器数量的增加,数据的分布越稀疏,从而导致学习器的维度也随之增加。而维度的增加会导致数据处理更为复杂从而增加运行时间。优化后的算法中第一层学习层和第二层学习层的分类器输入属性不同。第二层分类器输入属性的表达式如式6所示。
{(xn,yn,znt),n=1,2,...,N;t=1,2,...,T}
(式6)
式6中,znt表示第n个样本上第t个分类器的类概率向量预测值。第二层分类算法的训练集表达式如式7所示。
{(z1n,z2n,...,znt,yn),n=1,2,...,N}
(式7)
式7中,向量xn的维数大小用|xn|表示,所以第二层训练集的数据、属性大小保持不变。优化后的多层Stacking算法既保留了分类器的预测精度,又控制了计算成本从而缩短了运行时间,具有更高的性能。
(二)基于Stacking算法的模型融合装饰过程造价预测模型
每种算法都有其各自的优缺点,因此单一算法的预测模型因算法自身的理论差异,无法得出最优解[10]。模型融合算法可以平衡各算法之间的优缺点,在避免各算法因自身缺点导致的不足之外,还可以充分地发挥各算法的优势[11]。在工程造价预测领域常使用岭回归预测模型、随机森林预测模型以及XGBoost预测模型等进行造价预测分析。考虑数据结构的差异性,将这三种预测模型与Stacking模型相融合,以期提高装饰过程造价预测精度[12]。岭回归预测模型本质上是利用惩罚多元线性回归参数对损失函数添加正则化惩罚项,从而使参数更为平滑[13]。岭回归预测模型目标函数表达式如式8所示。
(式8)
Z=XTY(δI+XTX)-1
(式9)
式9中,(δI+XTX)表示满秩矩阵,回归参数的性能随着岭参数δ的变化而变化。随机森林预测模型属于经典的Bagging模型,是以多个弱学习器为决策树组合而成[14]。随机森林预测模型首先在原始数据的基础上随机抽样来生成不同的样本特征和样本数量,然后根据生成的样本构成不同的决策树模型,最后依据决策树模型的平均值得出最终结果[15]。随机森林预测模型如式10所示。
(式10)
式10中,A表示决策树数量,fa(x)表示第a棵决策树。随机森林预测模型的工作原理如图2所示。
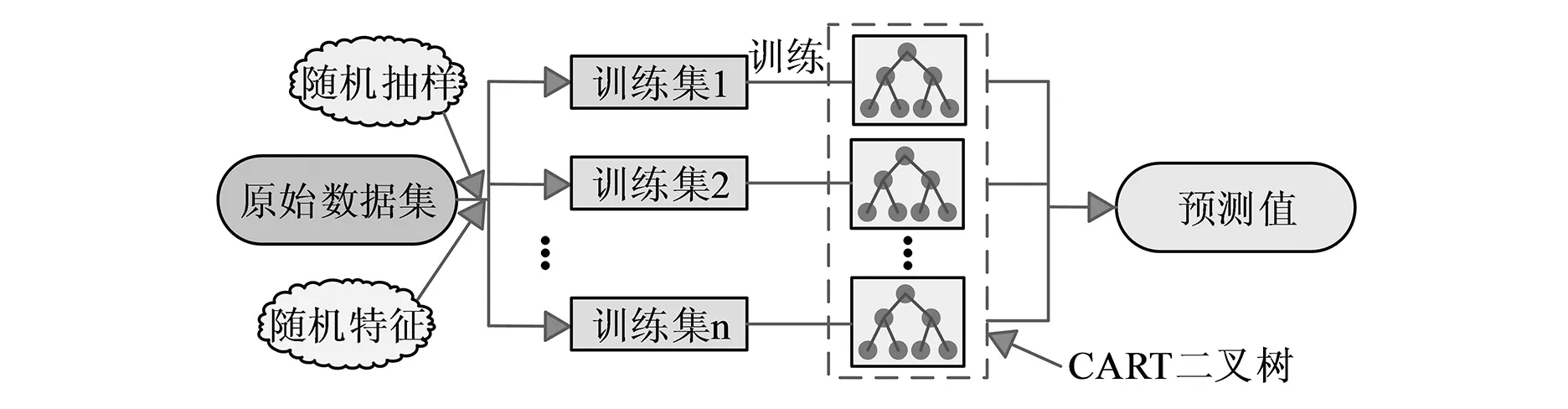
图2 随机森林预测模型的工作原理
由图2可以看出,影响随机森林预测模型性能的是决策树数量A和随机选择的特征数量max_features这两个参数。决策树的数量会影响预测模型的预测效果,当决策树数量太少时,会出现模型过拟合的现象,导致模型预测的效果不明显。而随机特征数量max_features的值越小,随机森林生成的决策树差异性就越大。与单独的决策树模型相比,随机森林预测模型含有的两个参数具有随机性,使得随机森林泛化能力更强且不容易出现过拟合现象,预测结果更为准确。XGBoost预测模型是由Boosting算法结合多个决策树的可拓展Tree boosting算法模型,其本质上是输入数据经过迭代训练生成新的决策树模型。在进行迭代训练中,每一次的迭代都会弥补上一轮的不足,因此得到的最终结果是经过数次迭代后的累加结果,该结果具有准确性高和运行速度快等优点。XGBoost预测模型如式11所示。
(式11)
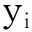
(式12)
式12中,Gj=∑i∈Ijgj表示样本的一阶导数,Hj=∑i∈Ijhi表示样本的二阶导数。影响XGBoost预测模型性能的是决策树数量B和决策树最大深度max_depth这两个参数,决策树最大深度max_depth的值越大,模型越容易出现过拟合现象,所以在参数设置时一般设置默认参数max_depth=6。结合以上三种预测模型的优点与Stacking算法模型相融合,基于Stacking算法模型融合如图3所示。
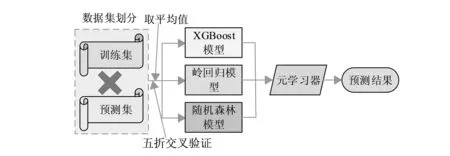
图3 基于Stacking算法模型融合
由图3可以看出,基于Stacking算法融合模型输入的数据集经过五折交叉验证得出新的训练集和预测集,模型融合的第一层即经过五折交叉验证的岭回归、随机森林以及XGBoost等算法的训练和预测结果,第二层是Stacking模型融合的元学习器,结合第一层的训练和预测结果,计算获得最终的预测结果。
二、基于模型融合的装饰过程造价预测模型验证
为了验证基于模型融合的装饰过程造价预测模型性能,将Stacking融合模型与单一的岭回归预测模型、随机森林预测模型以及XGBoost预测模型进行对比验证。设置岭回归模型的岭参数δ=0.62,随机森林决策树数量参数A=200,特征数量参数max_features为随机,XGBoost预测模型决策树数量参数B=7,决策树最大深度参数为默认参数max_depth=6,仿真计算出各模型的平均绝对百分误差MAPE和均方根误差RMSE 值并进行对比分析,各模型的MAPE和RMSE 对比如图4所示。
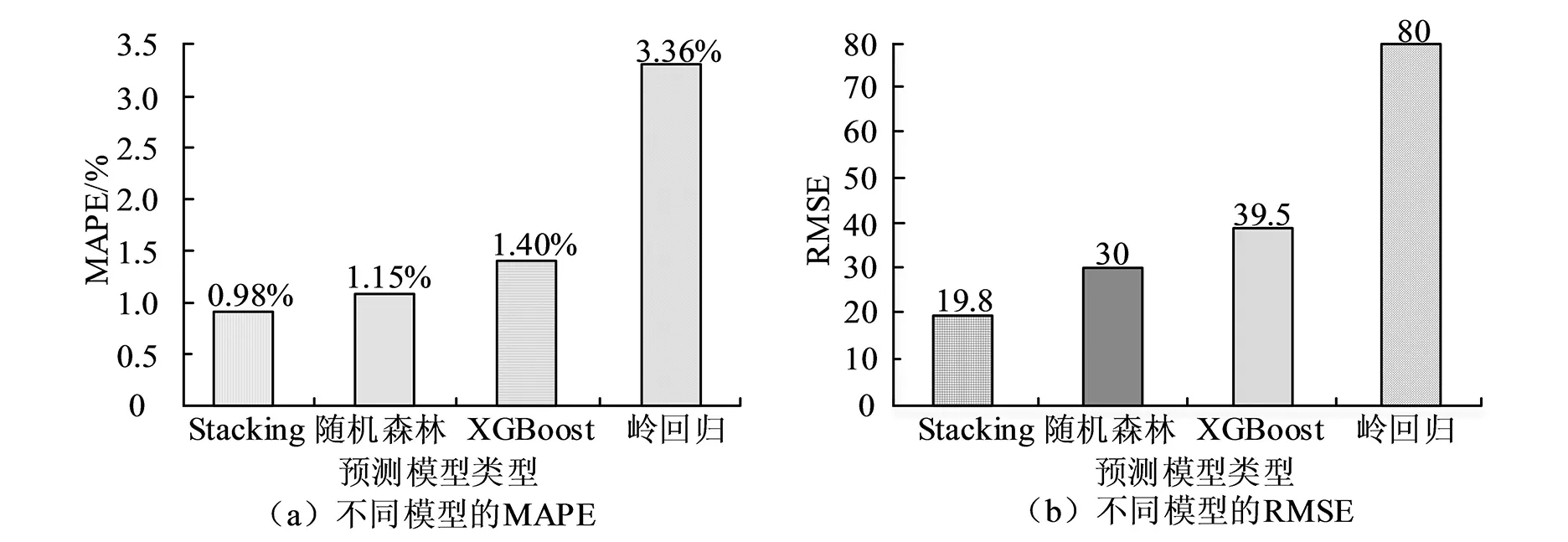
图4 各模型的MAPE和RMSE 对比
从图4(a)可以看出,Stacking融合模型的平均绝对百分误差MAPE值为0.98%,与其他三个预测模型的MAPE值相比是最低的,其中比岭回归预测模型的MAPE值3.36%低2.38%,比XGBoost预测模型的MAPE值1.4%低0.42%,比随机森林预测模型的MAPE值1.15%低0.17%,说明Stacking融合模型的预测准确性高于其他三种单一的预测模型。从图4(b)可以看出,Stacking融合模型的均方根误差RMSE 值为19.8,与其他三个预测模型的RMSE 值相比是最低的,其中比岭回归预测模型的RMSE值低60.2,比XGBoost预测模型的RMSE 值低19.7,比随机森林预测模型的RMSE 值低10.2,说明Stacking融合模型的预测精度高于其他三种单一的预测模型。 在实际装饰过程造价预测中,除了要考虑预测精度外,还需要考虑预测效率,将Stacking融合模型与其他三个单一的预测模型在5个测试样本中的预测运行时间进行对比验证。各模型的运行时间对比如图5所示。
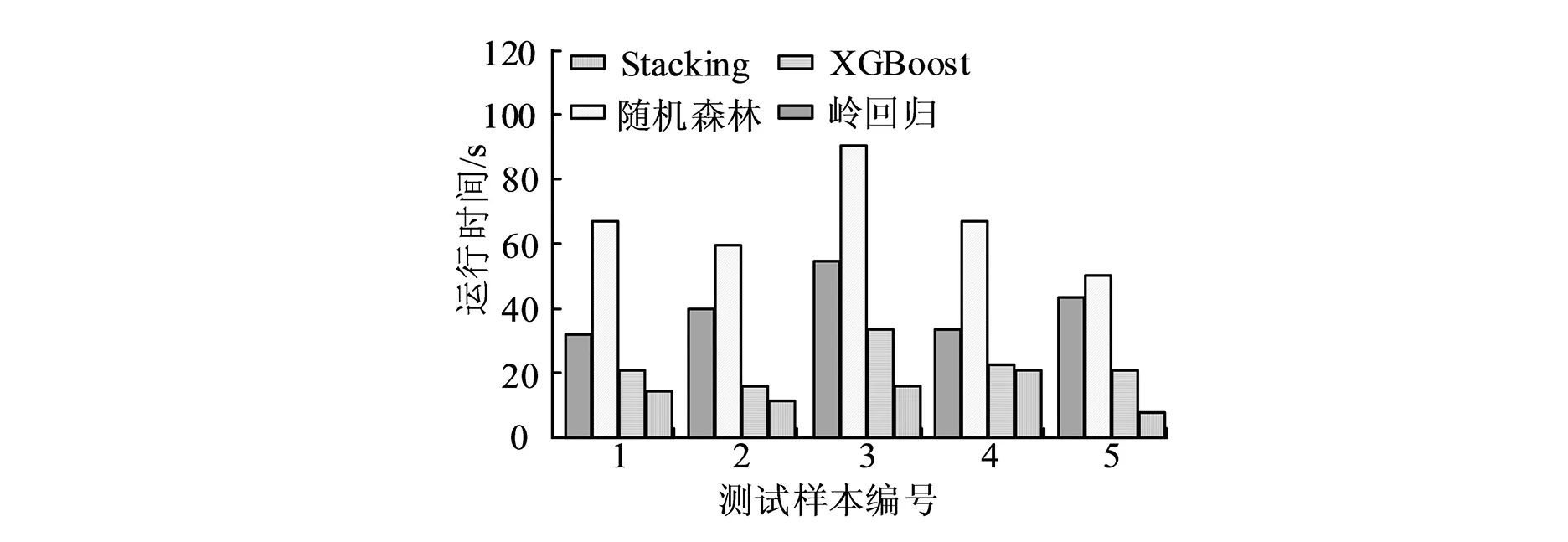
图5 各模型的运行时间对比
从图5可以看出,Stacking融合模型的预测运行时间明显少于其他三种预测模型,其中样本编号5的运行时间最短,为8s,比XGBoost预测模型的运行时间20s低12s,比随机森林预测模型的运行时间50s低42s,比岭回归预测模型的运行时间42s低34s。Stacking融合模型在样本编号4中的运行时间最长,为20s,比XGBoost预测模型的运行时间21s低1s,比随机森林预测模型的运行时间67s低47s,比岭回归预测模型的运行时间36s低16s。也就是说,Stacking融合模型的预测效率高于其他三个预测模型。
为了更直观地观测Stacking融合模型的性能,从测试样本中随机抽取原始数据绘制出Stacking融合模型的真实值与预测值并进行对比分析。Stacking融合模型的预测对比如图6所示。
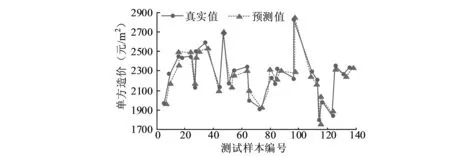
图6 Stacking融合模型的预测对比
从图6可以看出,Stacking融合模型的真实值与预测值走势几乎一致,说明真实值与预测值之间的绝对误差值较小,该模型的拟合能力较强。其中样本编号为63的绝对误差最大,此时预测值的单方造价为2100元/m2,真实值的单方造价为2000元/m2,真实值与预测值之间的绝对误差为100元/m2,此时的相对误差为5%。相对误差的值越低,说明预测精度越高,工程造价预测值的相对误差一般要求在10%以内。以上表明,Stacking融合模型的相对误差最大值为5%,说明该预测模型的预测精度较高,能够满足装饰过程造价预测的精度要求。
三、结论
为了能得到更高的装饰过程造价预测的效率和精度,研究基于模型融合的装饰过程造价预测模型,该模型利用Stacking融合模型融合了岭回归、随机森林以及XGBoost等算法,并在Stacking算法的基础上减少特征维数并增加一层初级层进行优化。仿真结果显示,研究的基于模型融合的装饰过程造价预测模型的预测精度和效率较高,满足装饰过程造价预测要求。但实验使用的样本数据较少,实验结果不够全面,这一方面还有待进一步完善。

