基于密度峰值算法的三支聚类

姜冬勤,王平心,杨习贝

(1.江苏科技大学 计算机学院, 镇江 212100)

(2.江苏科技大学 理学院, 镇江 212100)

传统聚类算法大多属于二支聚类,即类簇之间有着清晰的边界,但在实际应用中常常会遇到信息不充分的情况,如果将信息不充分的数据对象强行划分到某一类簇,会造成误分类的概率增加,导致聚类精度降低.针对传统聚类方法的不足,文献[1]将三支决策的思想引入到聚类分析中并提出了三支聚类算法[2-3].不同于传统的硬聚类,三支聚类用核心域和边界域来描述一个簇,能够更加精确的描述类簇的结构特征.基于这一框架,近年来,三支聚类研究也取得了大量的成果[4-8].文献[9]提出了密度峰值聚类(clustering by fast search and find of density peaks, DPC)[9],可以识别任意一个形状的类簇,而且可以自动地确定每个类簇的质心,克服了DBSCAN面临的不同类簇的密度差别大、邻域范围难以确定等问题.但DPC算法存在以下不足:① 截断距离dc需要人工设置,具有随机性;② 假如一个样本分配错误,就会带来后面一系列的分配错误.

为了对DPC算法的优化,文献[10]提出利用k-近邻来定义局部密度,且给了两种新的分配策略;文献[11]计算点到它的k-最近邻点的距离作为局部密度,并使用k最近邻点和模糊加权k-最近邻点依次将剩余的点进行分配;文献[12]将k-最近邻引入局部密度计算中并提出了新的分配策略,提高了聚类准确度;文献[13]提出基于共享最近邻的DPC(SNN-DPC)算法,该算法结合共享最近邻,不仅消除了截断距离对DPC算法的影响,也避免了连带分配错误,但其算法需要人工选择k值,不可以做到自适应.

基于上述问题,文中引入了自然最近邻算法,使得每个数据点的邻居数不再依赖于手动设置的参数,而是自适应的根据每个点的自然最近邻获取邻居个数,以此来确定每个点的局部密度和距离,通过决策图选取聚类中心,再融合三支决策思想,满足论文中所给判定条件归入核心域,再将剩余点分配到边界域中,最终得到三支聚类的结果,数据集上的实验结果验证了算法的综合性能.

1 相关工作

1.1 密度峰值聚类算法

密度峰值算法的核心思想是聚类中心满足以下两点:① 聚类中心被密度比它低的近邻点包围;② 聚类中心之间的距离大.选取局部密度大、距最近的较大密度点的距离都很大的数据点作为聚类中心.因此DPC算法有两个待计算量为局部密度ρi和数据点距离δi.

第i个数据点的局部密度ρi为:

(1)

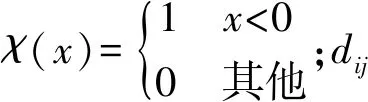
第i个数据点距离是指数据点的局部密度大于ρi,且与第i个数据点最近的点与该数据点之间的相对距离:

(2)

具体密度峰值算法流程如下:

算法1 DPC算法输入:数据集.输出:每个数据点的所属类簇.1: 初始化参数:截断距离dc.2: ① 计算任意两个数据点之间的距离;② 根据截断距离算出任意数据点的局部密度ρi;③ 对于任意数据点计算出其距离δi;④ 以ρi为横轴,以δi为纵轴构造出决策图;⑤ 利用决策图,选取ρi和δi都相对较大的值标记为聚类中心,选取ρi低但δi相对较高的点标记为噪声点;⑥ 将剩下的点划分到密度比它大且离它最近的数据点所属的簇.3: 输出:聚类结果.

1.2 自然最近邻居

最近邻算法中比较常用的是k-最近邻和ε-最近邻.k-最近邻是人为给定参数k,再找k个距离最小的样本点.ε-最近邻是人为给定半径ε,再找出每个样本点在其半径ε内的邻居个数.但这两种算法需要人工设定参数,人为因素直接影响结果,而自然最近邻很好的解决了这个问题.自然最近邻居[14](natural nearest neighbor, NNN)不需要设定任何参数,依靠数据集自身特点搜索得到,在密度较大的区域的点的邻居多,反之则邻居少.该算法可以很好地反映数据集的分布特征.

定义1(最近邻)NNr(xi)代表样本点xi的r最近邻,其中r由自然最近邻搜索算法自动生成.

定义2(逆近邻)RNNr(xi)表示样本点xi的r逆最近邻:

RNNr(xi)={xj∈X|xi∈NNr(xj),i≠j}

(3)

定义3(自然最近邻)NNN(xi)表示样本点xi的自然最近邻:

NNN(xi)={xj∈X|xi∈NNr(xj),xj∈RNNr(xi)}

(4)

定义4(自然邻居特征值supk)当所有的样本点都有逆近邻或者当样本中逆近邻个数为0的样本点个数不变时,自然近邻搜索过程到达自然稳定状态,此时的搜索次数称为自然特征值,记为:

supk={r|∀x∃y(y≠x∩x∈NNr(y))}

(5)

自然最近邻算法如下:

1.3 三支聚类

2010年,文献[15]提出三支决策理论,其核心思想是将研究对象分为POS(C)(正域)、NEG(C)(边界域)、BND(C)(负域),分别对应3种决策规则:接受、不承诺以及拒绝规则.

在三支聚类中类簇用Co(C)、Fr(C)、Tr(C)3个集合来表示,即为核心域、边界域和琐碎域.其中Co(C)中的样本点一定属于类C,Fr(C)中的样本点无法确定是不是属于类C,Tr(C)中的数据对象一定不属于类C[7].

在三支聚类过程中,琐碎域可通过Tr(Ci)=U-Co(Ci)-Fr(Ci)进行表示,并且在实际聚类中,划分出一定不属于某类簇的数据对象没有意义,对于一定属于某类簇的数据对象或者可能属于某类簇的数据对象,才是类簇划分与表示中的研究重点,文中划分只提供核心域与边界域的表示,表示结果:CS={{Co(C1),Fr(C1)},…,{Co(Ck),Fr(Ck)}},该式中集合满足如下性质:

(1)Co(Ci)≠∅i=1,2,…,k

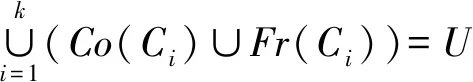
(3)Co(Ci)∪Fr(Ci)∪Tr(Ci)=U

性质(1)表明集合Co(C)不为空集,即每个类的核心域中至少要有一个对象.

性质(2)确保集合U中每个对象至少被划分到一个类中.

性质(3)要求任何一个类簇3个集合的并集为U.

2 基于密度峰值算法的三支聚类

2.1 基于密度峰值算法的三支聚类

基于SNN-DPC算法[13],引入自然最近邻算法,重新计算了局部密度和距离函数,消除邻域大小对聚类算法的影响.SNN-DPC中的SNN的实现依赖KNN算法,需要人为指定k值,选取的k值直接决定了算法结果的好坏,具有随机性.文中选择自然最近邻算法计算共享近邻,避免了参数选择的随机性,在此基础上融入三支决策思想,将传统的硬聚类转换成三支聚类,进一步提升了聚类的质量,由于三支聚类的特性,使得本算法更加贴合实际生活场景.所提算法即基于密度峰值聚类算法的三支聚类,简称3W-DPC.

定义5(共享近邻SNN)点i和j是数据集D中的任意两个点,点i和点j的自然最近邻集合分别为NNN(i)和NNN(j),那么它们的SNN为各自近邻集合的交集,记为:

SNN(i,j)=NNN(i)∩NNN(j)

(6)

定义6[16](共享近邻相似度Sim)点i和j是数据集D中的任意两个点,p是共享邻居集合里的点,Sim定义为:

(7)

式中:|SNN(i,j)|为点i和点j的共享邻居的数量,用|SNN(i,j)|除以点i和点j到所有共享邻居的距离之和可以视为这两点周围的密度,同时利用共享邻居数量和密度来定义相似度,得到的结果也更准确.仅当它们都位于彼此的自然最近邻中,才会计算两者的共享近邻相似度,否则相似度为0.

定义7(SNN局部密度)点i是数据集中的任一点,L(i)={x1,x2,...,xsupk}是与点i具有最相似的点的集合,点ρi的局部密度为L(i)内所有点相似度的和,记为:

(8)

如果自然最近邻域中的数据点分布较密时,该点密度就较大,反之较小.

定义8(数据点距离δi)点i是数据集中的任一点,j是局部密度比i高的点,p为点i的自然最近邻域集合中的点,q为点j自然最近邻域集合中的点:

(9)

对于密度最高的点,则可以取:

δi=max(δj)

(10)

很多数据集上的数据点分布并不均匀,通过上述计算方法,在数据点集中的区域缩短了数据点的距离δi,在数据点稀疏的区域放大了数据点之间的距离δi,考虑了每个点的邻居信息.

得到每个点的ρi和δi值后,生成决策图,并在图中选取ρi和δi都大的值作为聚类中心.

定义9设xi∈CI,CI为类簇中心集合,xj∈NNNnb(xi)(xi),如果满足下式,则归入核心域:

|NNNnb(xi)(xi)∩NNNnb(xj)(xj)|≥|NNN(xj)|/3

(11)

选择出聚类中心后,设聚类中心点xi有m个自然最近邻居,样本点xj是样本点xi的自然最近邻居之一且未被划分到核心类簇,样本点xj的自然最近邻居个数为n,如果此时样本点xj和样本点xi的共享自然邻居个数大于等于xj点自然最近邻居个数的1/3,则将xj归入聚类中心xi所属类簇的核心域,反之将样本点xj归为边界域.

经过上述处理得到核心域和边界域,针对边界域中的数据对象的处理策略是:将其划分到和该点最近的点xi在的类簇的边界域中.原则上,此类数据点是属于所属类簇的边界域,但是在计算聚类质量时,将同一类簇的核心域中数据点和边界域中数据点合并作为最终聚类结果,并在此结果集上评价聚类质量.由于边界域中的数据点存在更高概率的误分类,按照这样的计算标准,更加能证明所提出算法的优越性.

基于密度峰值算法的三支聚类算法如下:

算法3 基于密度峰值算法的三支聚类输入:数据集输出:数据点xi的所属类簇1:初始化参数:无2:① 计算任意两个数据点之间的距离; ② 计算每个数据点的自然邻居NNN(xi)以及该点邻居个数nb(xi); ③ 根据式(8)算出任意数据点xi的局部密度ρi; ④ 根据式(9)和式(10)得到任意数据点xi距离δi; ⑤ 以ρi为横轴,以δi为纵轴构造出决策图; ⑥ 构建决策图,选取ρi和δi都大的值标记为聚类中心CI={Co(C1),…,Co(Ck)}; ⑦ 取xi∈CI,xj∈NNNnb(xi)(xi),满足式(11),则xj归入xi所在类簇的核心域Co(xi); ⑧ 剩下的点归类到是它的最近邻并且密度大于它的数据点在的簇的边界域.3:输出:数据点xi的所属类簇.

2.2 算法分析

使用自然最近邻算法对DPC算法进行改进,将改进后的算法与三支聚类相结合,聚类的质量得到了进一步的保证,但三支聚类仅提供了一种进行软聚类的策略,即可以通过制定相对应的规则来规定不同数据簇的核心区域和边界区域,具体的规则实现各有不同,但都不可避免地要进行相关阈值参数选取.由专家经验可得,此阈值参数一般可设置为1/2、1/3或1/4.文中选取1/3作为三支聚类的阈值,在人工数据集Aggregation上验证不同阈值的聚类质量,以证明该参数的合理性及鲁棒性.图1显示不同阈值下的聚类结果,表1则对应着不同阈值下的性能评价结果,包括准确率(accuracy,ACC) 、调整兰德指数(adjusted rand index,ARI)、调整互信息(adjusted mutual information,AMI)和FM指数(fowlkes and mallows index, FMI).

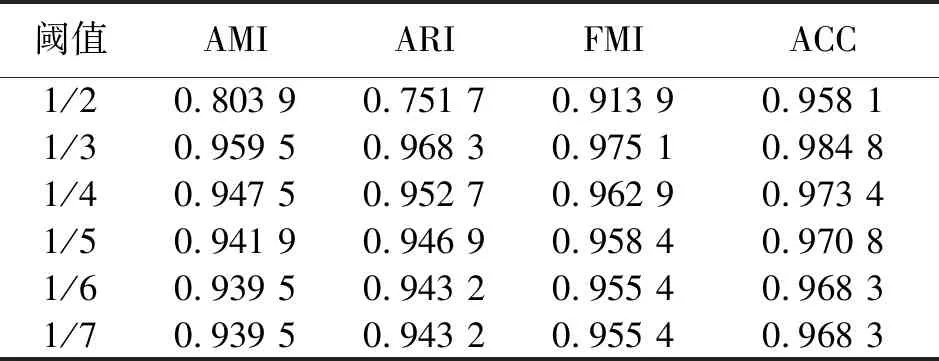
表1 不同阈值聚类结果

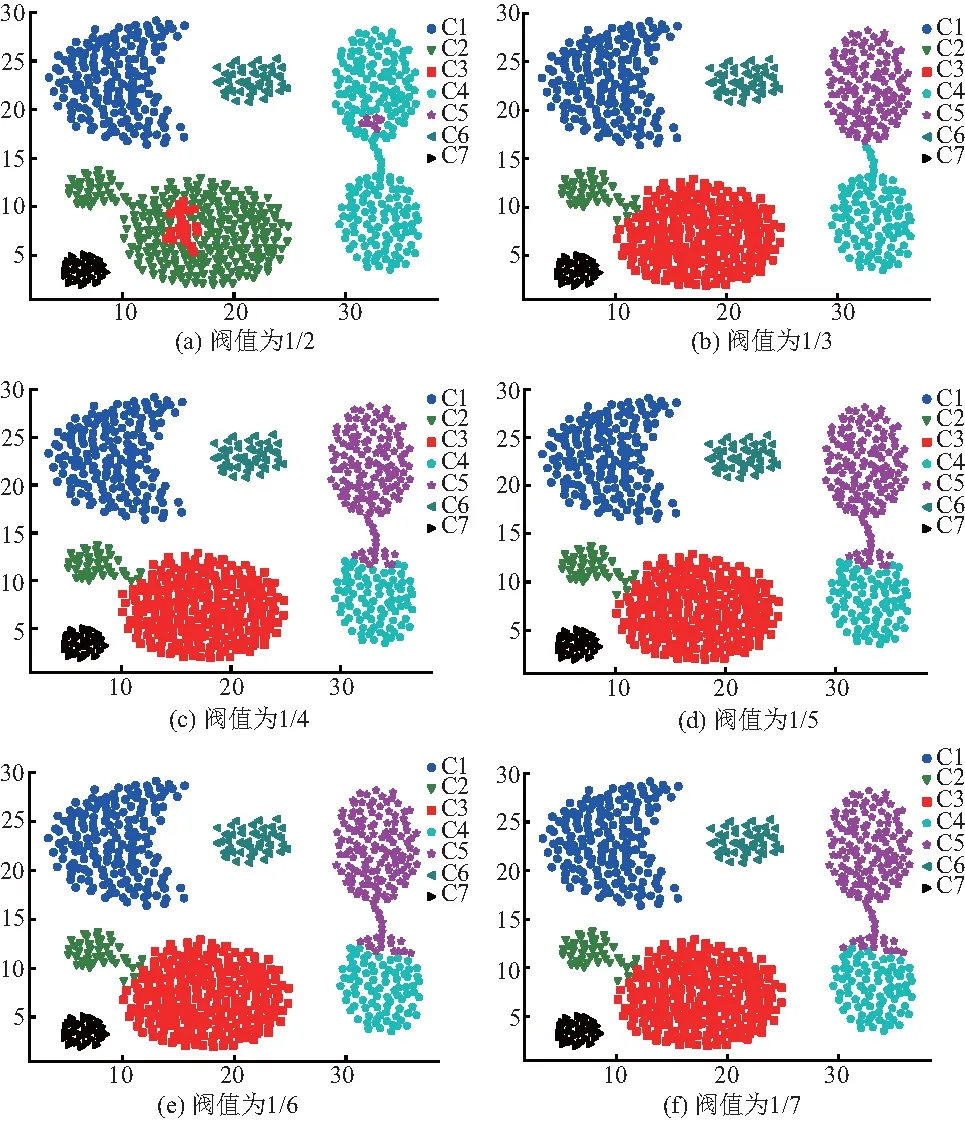
图1 不同三支阈值下3W-DPC在Aggregation上结果

从图1中的6个子图中可以看出,当阈值由1/2减小为1/7时,聚类的效果由差到好再到差,即存在一个聚类效果峰值,这个峰值对应的阈值恰好为1/3.由图1(a)可以看出原本属于C3的数据对象被错误地分配到了C2,同样地,C5和C6也存在这样的问题;观察图1(b)、(c)和(d),着眼于C3,图1(b)的聚类结果要稍逊于图1(c),因为其在C3存在3个数据对象的误判,但在C4上,图1(b)的聚类结果要明显好于图1(c),图1(c)在C4上存在15个点左右的误判,图1(d)相较于图1(c),在C3上多了3个数据对象的误判,综合看来,三者之中图1(b)更加优秀;同样地,可以看出图1(b)要优于图1(e)和(f).

由表1可以看出,当阈值选取为1/3时,各项指标表现最为优异,与图1分析一致.且仔细观察可知,当阈值选取小于1/6时,各项性能指标不会随着阈值的减小而变化.分析式(11)可得,阈值与因子NNN(xj)相乘作为判定的条件,当两者相乘的结果小于1,便不会对数据集区分出粒度,式(11)的效果也就等价于如果xj与核心点xi存在交集,则将xj归入核心点xi所属类簇,虽然这样也属于是三支聚类的一种策略,但是设置的区分粒度太大,聚类效果可能不好,通过分析,结合自然邻居的特性可知,当阈值小于1/Max(nb(xi)),便不会产生区分粒度的变化.由专家经验可得这个阈值在1/2至1/Max(nb(xi))产生,通过实验证明选取1/3作为阈值具有一定的优越性和鲁棒性.

2.3 复杂度分析

2.3.1 空间复杂度分析

每个数据对象到所有数据对象(包括自身)的空间复杂度,即存储距离矩阵为O(N2),其中N为数据对象总个数,存储每个数据对象的自然邻居个数的空间复杂度为O(N*supk),supk为稳定状态时的搜索次数.所以3W-DPC算法空间复杂度为O(N2),和原始密度峰值算法一样.

2.3.2 时间复杂度分析

3W-DPC算法时间复杂度主要取决于:

(1) 每个数据对象的距离矩阵,其时间复杂度为O(N2);

(2) 每个数据对象的自然邻居,因为将数据放入k-d树,使用了k-d进行搜索,搜索i的第r个近邻时间复杂度为O(log(N)),因此时间复杂度为O(supk*N*log(N));

(3) 局部密度ρ,由自然最近邻集合可知时间复杂度为O(supk*N);

(4) 数据点距离δ,时间复杂度为O(N2)找到中心点并将剩余点分配到其属于的类簇,时间复杂度为O(N2),所以总的时间复杂度为O(N2),与未该改进前的DPC算法相同.

3 实验仿真

选用2组Synthetic数据集、5组UCI数据集和4组Shape(人工)数据集[17]进行实验.数据集如表2～4.

表2 Synthetic数据集

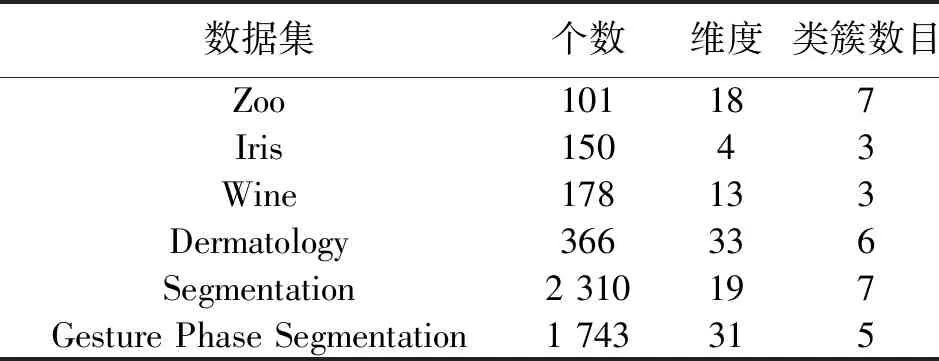
表3 UCI数据集

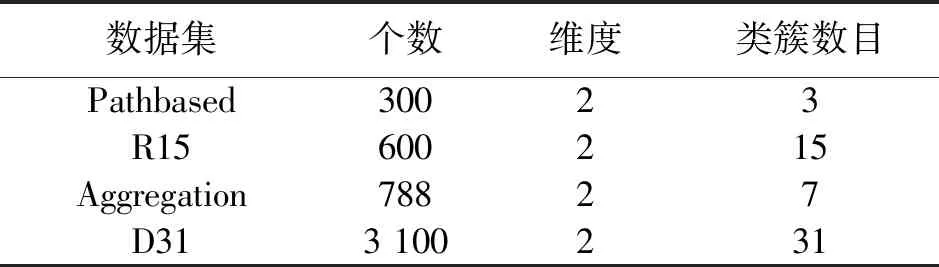
表4 Shape数据集

不同的数据集有不同预处理方式,对于UCI数据集,由于该数据集中会出现不是数字或者为空的属性,也就是类别型属性,这类属性往往存在离散值问题,既想保留尽可能多的数据信息,同时也要考虑到字符数据的离散程度,所以需要将不是数字的属性进行One-hot编码,然后,进行归一化处理,使得每个维度所占比重相同.对于Shape数据集和Synthetic数据集,由于不会出现不是数字的属性,所以只进行归一化处理.

4 实验结果

3W-DPC算法与传统DPC,SNN-DPC算法在数据集上进行实验对比,实验结果如表5～7.

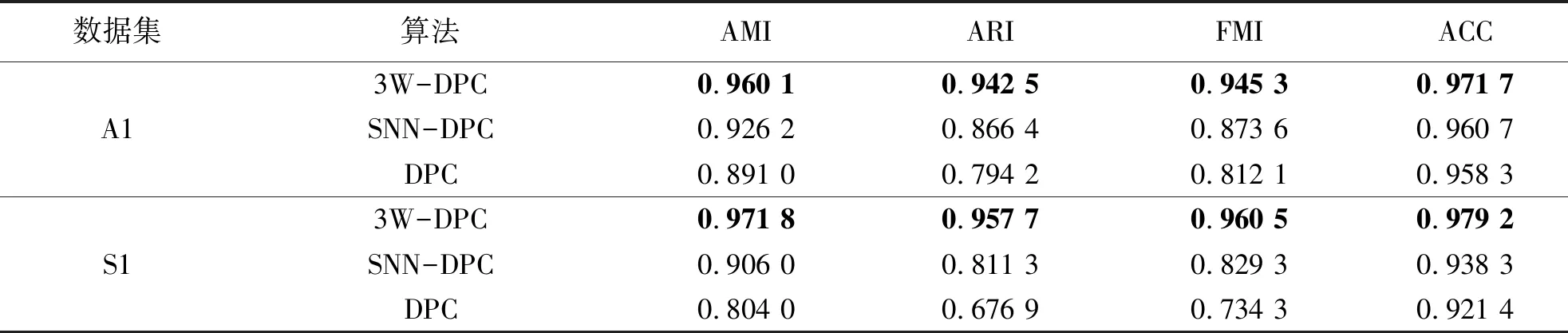
表5 Synthetic数据集上的实验结果

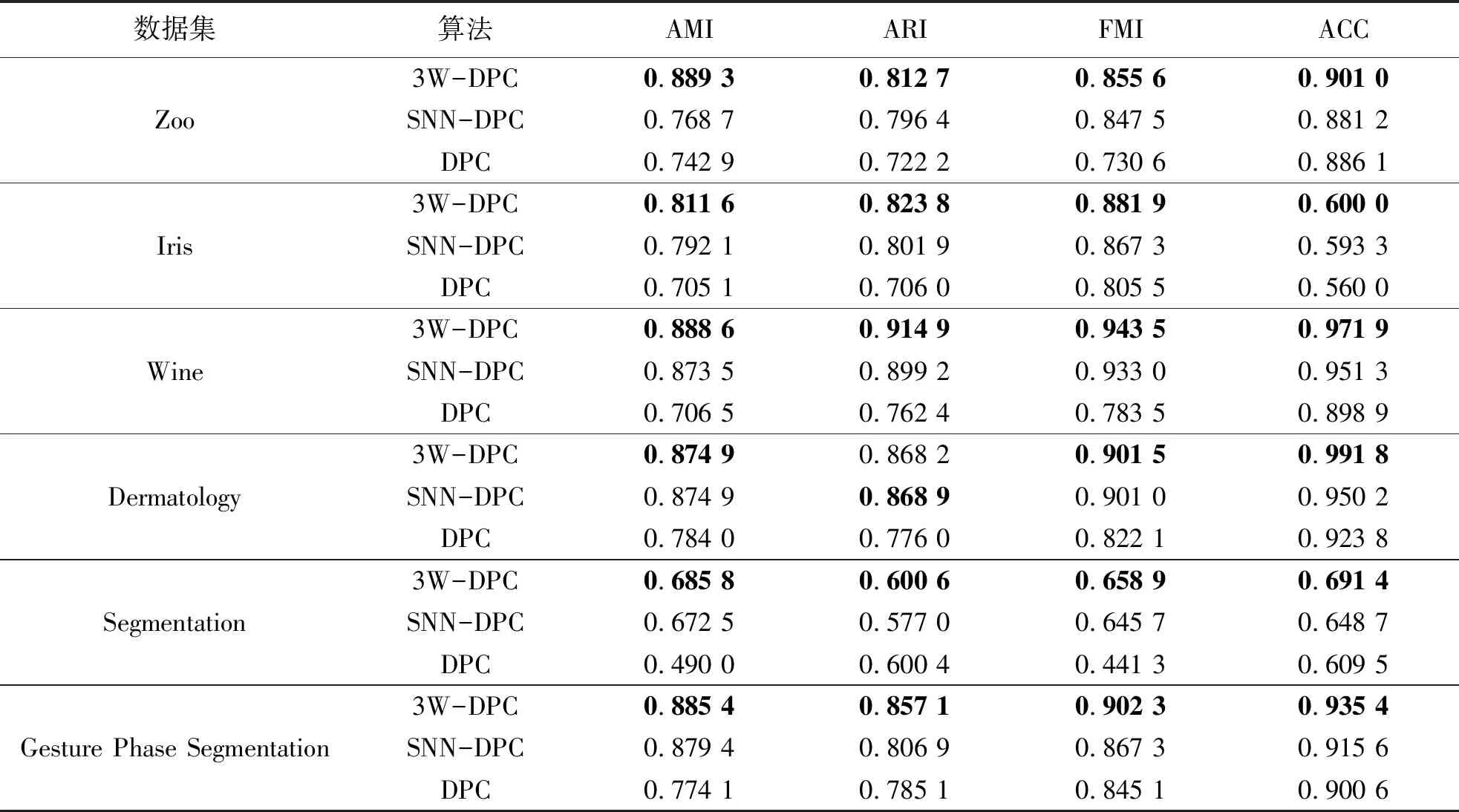
表6 UCI数据集上的实验结果

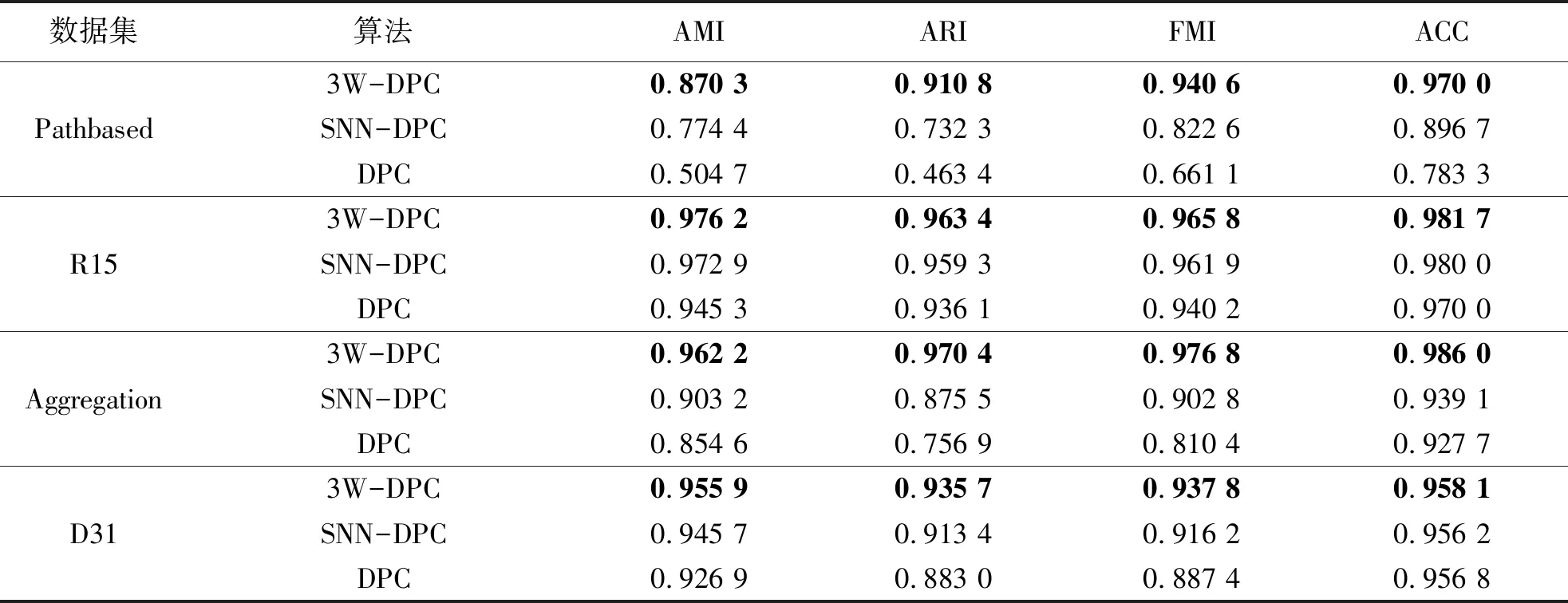
表7 Shape数据集上的实验结果

从表5～7中的实验结果可以看出,在AMI、FMI、ACC指标上,提出的3W-DPC算法相比于SNN-DPC、DPC算法明显优秀很多.在ARI指标上,也只有Dermatology数据集,SNN-DPC比SNN-DPC结果稍好,其余数据集上3W-DPC算法都是比3W-DPC、DPC算法优秀.3W-DPC算法与SNN-DPC、DPC算法的聚类结果相比,有效提升了算法性能.

5 结论

(1) 借助自然最近邻算法提出了一种基于改进的DPC算法的三支聚类.该算法首先利用自然最近邻定义共享邻居,确定DPC算法的两个待计算量:局部密度βi和数据点距离δi,通过决策图得到密度峰值点,即聚类中心,解决了需要人为指定k值的不足.

(2) 算法融合了三支聚类,通过阈值将确定的元素划分到核心域,将不确定的元素划分到边界域延迟决策,在多组数据集上进行了实验验证,并与SNN-DPC、DPC算法进行比较,实验结果表明此方法可以提高聚类的精度以及提升算法的性能表现.

(3) 自然最近邻是一个新兴的邻居概念,有关定义以及应用有待完善,在后续工作中,将讨论如何利用自然最近邻更贴切的定义DPC算法的两个计算量,以及对不确定元素进行更巧妙的分配.