通货膨胀对经济增速放缓福利成本的影响研究

赵鑫铖

(云南大学 经济学院, 昆明 650091)

事实上,推动经济增长和保持物价稳定都有助于社会福利水平的提升:经济增长提高了消费者的收入,进而直接提高了消费者的福利水平;而保持物价稳定则由于消除了通货膨胀带来的扭曲效应、再分配效应等对消费者福利负面影响,从而提高了消费者的福利水平。从理论上讲,政府应该同时实现这两个目标来促进社会福利的提高。但在实际中这两者总是矛盾的。那么,在我国经济进入中高速增长的新时期,经济增长速度的放缓必然带来居民福利的损失,也就是经济增长放缓存在福利成本,通货膨胀对这一福利成本将产生什么样的影响?是否能通过稳定通货膨胀进而降低这一福利成本?回答这两个问题,对准确把握和处理我国“保增长”和“防通胀”之间的关系,实现我国经济高质量发展具有重要的理论和现实意义。

1 文献综述

学术界对经济增长福利成本的定量研究起步较晚,主要原因在于学界普遍认为经济增长对社会福利的影响非常大,一个百分点增长率差别经过较长时间的作用将会引起巨大的福利差别。Lucas[1]建立了利用客观指标来间接计算经济周期与降低经济增长福利成本的基本模型,开创了通过运用宏观经济模型测算福利效应的先河。其所用方法被归纳为“消费等价补偿”,如经济增长的福利收益可描述为,对于消费者来说,在初始消费相同的情况下,当面临零增长和一定数值增长的两种消费路径时,偏好后者,因此必须对零增长的消费路径进行补偿以使消费者对两者感觉无差异,这一补偿的比例就是经济增长的福利收益。Lucas运用美国数据的实证分析表明,消除经济周期的福利收益为0.32%,而经济增长降低一个百分点的福利成本为20%,进而得出了经济增长远比消除经济波动重要的观点。在Lucas分析框架的基础上,陈彦斌[2]、饶晓辉和廖进球[3]运用CRRA效用函数研究我国经济增速放缓的福利成本,结论表明中国经济增速放缓一个百分点的福利成本非常大,且大于美国的水平。陈太明[4]基于CRRA效用函数的经济增速放缓福利成本测算模型,运用全国城乡、省级、省级城乡居民消费数据评估经济增速放缓给异质居民带来的差异化福利影响。Okubo和Masakatsu[5]指出,经济增速放缓的福利成本非常大,且这一成本随着经济增长速度的提高而降低,也就是说当经济增长速度由7%降低为6%的福利成本小于由3%降低为2%的福利成本。

关于通货膨胀福利成本的研究相对较多,从测度方法来看,可以分为以下几类:一是均衡模型,Bailey和Martin[6]基于货币市场均衡提出了消费者均衡模型来度量通货膨胀的福利成本,信用货币体制下货币的生产成本基本可以忽略,因此货币的福利成本可以用货币需求曲线下方的面积度量,设定货币需求函数为双对数型和半对数型的情况下,名义利率为6%时美国通货膨胀的福利成本分别为消费水平的1%和0.3%。二是新古典宏观经济学一般均衡模型,具体包括内含货币效用(money-in-the-utility function,MIU)模型、购物时间模型、现金优先(cash-in-advance,CIA)模型、货币搜寻模型、不完全市场模型、家庭异质性模型等。三是基于幸福经济学的模型研究,何强[7]在经典货币效用模型中引入幸福经济学中的习惯形成效应拓展消费者效用函数,建立了通货膨胀的福利成本理论测度模型。陈刚[8]另辟蹊径采用2006年中国综合社会调查的微观调查数据,从幸福经济学的角度,测度了通货膨胀率变动对居民幸福感的影响程度,发现通货膨胀率每提高1个百分点,将会使国民幸福感降低约1.13个百分点,相应地需要GDP增长率提高2个百分点才能弥补幸福感降低的缺口。

当前关于经济增长福利成本和通货膨胀福利成本的单独研究俯拾皆是,但由于经济增长主要关注经济的长期方面而通货膨胀则关注经济的短期方面,将二者放在同一理论框架下进行比较研究并不容易,国内鲜有学者进行研究。肖争艳和姚一旻[9]运用Lucas消费等价补偿方法比较了我国通货膨胀再分配效应导致的福利成本和经济增长放缓的福利成本,但由于其采用数据的原因,该方法并不具备推广的可能性。李强[10]通过数值模拟得出在考虑通货膨胀后经济增长率下降所产生的社会福利损失,利用中国的实际宏观数据分析不同经济发展情形下的社会福利变化。

本文从福利视角来研究通货膨胀对经济增速放缓福利成本的影响,进而为我国的宏观经济政策提供决策参考。

2 理论模型

遵循Lucas模型逻辑,假定具有无限生命的代表性消费者最大化其一生期望效用水平为

(1)

式中:E为期望算子;ct为t期的实际消费;θ为消费者的相对风险规避系数;β为贴现因子,反映代表性消费者对未来的耐心程度。

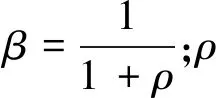
(2)

消费者的消费流服从如下随机过程:

ct=A(1+g)te-0.5σ2zt

(3)

式中:zt是一个独立同分布的随机过程,服从均值为0、方差为σ2的对数正态分布,即有lnzt～N(0,σ2);g为消费增长率;A为常数在这些假设条件下,有E(e-0.5σ2zt)=1。因此,E(ct)=Aegt。

(4)

λ(g0,g1)为如下方程的解:

(5)

求解式(5),得

(6)

Lucas给出了相对风险回避系数θ等于1时的经济增长速度变化的福利成本为

(7)

由式(6)可知,经济增速放缓的福利成本λ(g0,g1)不仅与变化前后的经济增长率有关,而且与相对风险回避系数θ和通货膨胀率π0有关。求福利成本关于通货膨胀的偏导数,得

(8)

此外,相对风险规避系数θ越大,经济增长的福利成本越小。也就是说,经济增长的福利成本随相对风险回避系数增加而降低,这只是一个推导结果,其经济学机理是什么?由于相对风险回避系数衡量的是消费者对待风险的态度,而经济增长与消费者对风险的态度并无直接关系,且从风险角度不容易将经济增长的福利成本与代表性消费者的相对风险回避系数关系讲清楚,且使用的是CRRA效用函数,在CRRA效用函数设定下,消费者的相对风险回避系数与跨期替代弹性互为倒数,即有ϑ=1/θ。因此,从替代弹性的角度讨论相对风险回避系数对通货膨胀和经济增长福利的影响。考虑消费者跨期替代弹性(相对风险回避系数)对经济增长福利成本的影响。当消费者的跨期替代弹性ϑ较小(相对风险回避系数θ较大时),消费者不愿意牺牲当前消费来换取更多的未来消费,从而使得通过减少当前消费换取未来收入增长进而消费增长的福利成本较小;反之,当消费者的跨期替代弹性ϑ较大(相对风险回避系数θ较小时),消费者愿意延迟消费来换取更多的未来消费,从而使得通过减少当前消费换取未来收入增长进而消费增长的福利成本较大。

3 通货膨胀对经济增长福利成本影响的实证研究

3.1 数据来源及参数校准

要测算经济增长福利成本,根据式(6)、式(7),需要获得经济增长率g、通货膨胀率π、相对风险回避系数θ、实际利率r等数据和参数。

3.1.1 经济增长率的估计

理论模型中,经济增长率用消费增长率进行衡量,实证分析部分也运用消费增长率来代替经济增长率,这主要基于几个方面的考虑:首先,消费者的效用函数直接定义在消费水平之上,因此使用消费比使用人均GDP等收入指标更加直接也更加方便;其次,从收入与消费的实证研究结果来看,两者之间存在较为稳定的线性关系,因此理论上用消费增长率来代替GDP增长率在本质上是相同的;再次,在动态一般均衡模型中,在经济的稳态上,消费增长率等于产出(经济)增长率;最后,由于主题是福利分析,消费水平比收入水平更能代表福利水平。人均消费数据是《中国统计年鉴2019》国民经济核算部分的居民消费水平,运用居民消费价格指数转换为以1978年为基期的实际数据。依据模型对消费的假设,对式(3)两边取自然对数,进而得到对数消费的一元线性回归模型:lnct=(lnA-0.5σ2)+gt+lnzt,时间趋势项t的系数即为消费的增长率。出于对经济发展阶段性的考虑,选取1978—1992年、1992—2018年和1978—2018年3个样本区间比较经济增速放缓的福利成本和消除通货膨胀的福利收益。两个样本区间消费增长率的估计值如表1所示。

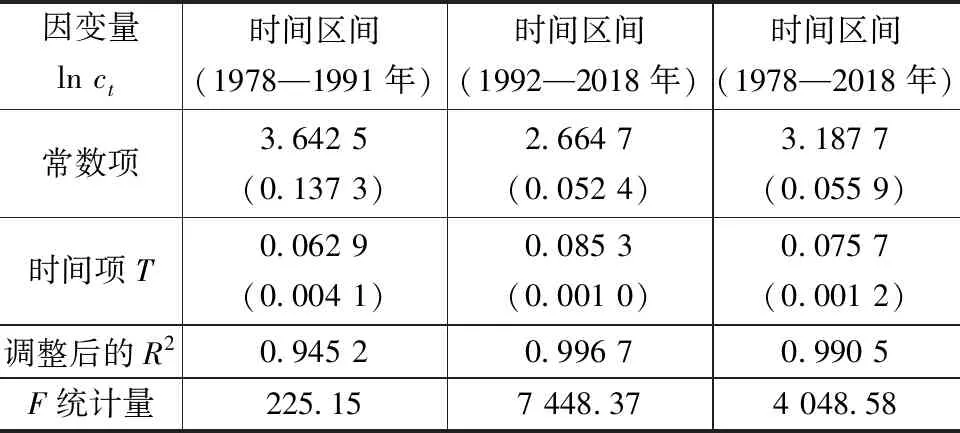
表1 样本区间消费增长率的估计

3.1.2 其他参数的校准

对于实际利率r,从均衡利率和自然利率两个角度来考虑其校准问题。贺聪等[12]构建了一个包括家庭、企业、银行和中央银行的四部门DSGE模型测算我国的均衡利率,测算结果表明,截至2012年第3季度我国的均衡利率为2.57%。姚翔等[13]构建了一个具有永久性趋势冲击和风险偏好冲击的动态随机一般均衡模型测算我国的自然利率水平,得出在2010—2018年的自然利率均值为2.55%。因此,将实际利率校准为2.50%。

对于通货膨胀率π,将《中国统计年鉴2019》中居民消费价格指数转换为1978年为基期的价格指数,1978—1991年、1992—2018年、1978—2018年3个样本区间的平均通货膨胀率分别为6.40%、4.02%和4.87%。

对于相对风险回避系数θ。虽然在理论模型中,经济增长与通货膨胀福利成本的影响分析中,运用跨期替代弹性ϑ进行阐述,但出于与同类研究进行比较的考虑,仍然相对风险回避系数θ来进行校准,取1、5、10、20等4个数值。

3.2 经济增长速度降低的福利成本

根据上述参数校准和式(6)、式(7),可以计算出经济增速放缓1个百分点的福利成本(表2)。由于在1978—1991年、1992—2018年和1978—2018年样本区间有不同的通货膨胀率和经济增长率,因此在相对风险回避系数取值相同的情况下,各阶段经济增速放缓1个百分点的福利成本λ(g0,g0-1%)体现出一定的差异性。首先,在其他参数给定的情况下,经济增速放缓一个百分点的福利成本随着相对风险回避系数θ的提高而下降,以1992—2018年为例,当通货膨胀为4.02%和其他参数为校准基准值的情况下,相对风险回避系数从1分别上升到5、10和20时,经济增长速度从8.53%下降到7.53%(即下降1个百分点)的福利成本从15.25%分别下降到2.08%、0.82%和0.26%;其次,在通货膨胀和其他参数给定的条件下,相对风险回避系数取其较为合理的中间值θ=5时,中国经济增长速度下降1个百分点的福利成本在1978—1991年、1992—2018年和1978—2018年分别为2.64%、2.08%、2.30%,也就是说,需要将代表性消费者的消费水平永久性地分别提高2.64个百分点、2.08个百分点、2.30个百分点才能使其愿意接受在1978—1991年、1992—2018年和1978—2018年消费增长率分别下降1个百分点。最后,在考虑通货膨胀影响条件下,测算了我国经济增长速度下降1个百分点的福利成本,其数值与国内其他学者的分析基本一致[2,4],其范围为[2.08%,2.64%]。

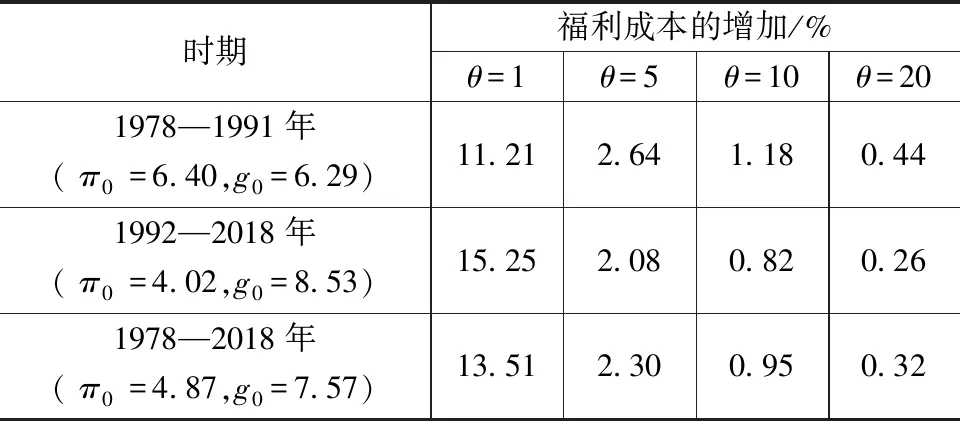
表2 经济增速放缓1个百分点的福利成本λ(g0,g0-1%)

模型分析部分已证明,经济增速放缓1个百分点的福利成本与通货膨胀率呈负相关关系,表3给出了通货膨胀率与经济增速放缓1个百分点(由8%降低到7%)的福利成本的数值模拟结果。一方面,证实了经济增速放缓福利成本与通货膨胀率之间的负相关关系,例如当θ=5时,通货膨胀率分别为1%、5%和10%对应的经济增长速度降低1个百分点(由8%下降为7%)的福利成本分别为2.47%、2.16%和1.87%;另一方面,通货膨胀对经济增速放缓1个百分点(由8%降低到7%)的福利成本负向影响随着相对风险回避系数的提高而减小,如通货膨胀率从5%提高到10%时,θ=1经济增速放缓1个百分点的福利成本由13.21%下降到7.73%,θ=10经济增速放缓一个百分点的福利成本由0.88%下降到0.81%。

表3 通货膨胀与初始经济增长率对经济增速放缓1个百分点的福利成本的影响

另外,表3也模拟了不同的初始经济增长率对经济增速下降1个百分点的福利成本的影响。结果表明,在其他参数取值相同的情况下,初始经济增长率越低,经济增速放缓1个百分点的福利成本越大,如当θ=5时,给定初始经济增长率分别为1%、5%、10%,经济增速下降1个百分点的福利成本分别为11.04%、3.46%和1.69%。

随着我国经济进入新常态,经济增长从高速向中高速转变,经济的这一转变将使得中国居民消费增长率下降近2个百分点,这将对我国居民的福利产生重要的影响。为了评估新常态导致的经济增长率下降对居民福利的影响,假定居民消费增长率从1978—2018年的7.57%下降2个百分点为5.57%,经济进入新常态后中国通货膨胀率保持在较为温和的3%水平,将实际利率校准为2.50%。根据式(6)、式(7)得新常态经济增速放缓2个百分点的福利成本(表4)。

表4 新常态经济增速放缓2个百分点的福利成本λ(g0,g0-2%)

经济增速下降2个百分点的福利成本随相对风险回避系数的递增而减少,其取值范围为[0.75%,40.67%]。实证研究中,相对风险回避的合理取值范围为[1,5]。考虑当θ=5时,新常态下经济增速放缓2个百分点导致的福利成本为5.38%,也就是说需要将代表性消费者的消费水平永久性地提高5.38个百分点才能使他愿意接受消费增长率下降2个百分点,按2018年我国居民的消费水平为25 002元衡量,这意味着由于消费增长率下降2个百分点需要永远给每个消费者补偿1 345元才能使其福利水平保持不变。

4 结论与启示

4.1 结论

第一,通货膨胀通过影响代表性消费者的贴现行为而对增速放缓福利成本产生影响。

第二,经济增速放缓的福利成本随着通货膨胀的提高而降低,其直观解释为,较高的通货膨胀使得由经济增长的引致消费者实际消费大幅减少,从而用消费比例衡量的福利成本就相对较低。

第三,经济增速放缓的福利成本随着相对风险回避系数的提高而减少,从替代弹性的角度进行了阐述:当消费者的跨期替代弹性ϑ较小(相对风险回避系数θ较大时),消费者不愿意牺牲当前消费来换取更多的未来消费,从而使得通过减少当前消费换取未来收入增长进而消费增长的福利成本较小。

第四,实证研究证实了理论推导中得出的经济增速放缓的福利成本随通货膨胀和相对风险回避系数的提高而降低,在通货膨胀和其他参数给定的条件下,相对风险回避系数取其较为合理的中间值θ=5时,中国经济增长速度下降1个百分点的福利成本在1978—1991年、1992—2018年和1978—2018年分别为2.64%、2.08%、2.30%。

第五,测算了新常态经济增长由高速向中高速转变的经济影响,新常态下经济增速放缓导致的福利成本为5.38%,也就是说需要将代表性消费者的消费水平永久性地提高5.38个百分点才能使他愿意接受消费增长率下降2个百分点。

4.2 建议

第一,在经济发展过程中尽可能稳定通货膨胀和通货膨胀预期。由于通货膨胀能够影响代表性消费者的行为,进而影响经济增速放缓的福利成本:低通胀带来较高的增速放缓福利成本,高通胀带来较低的增速放缓福利成本。

第二,在采取措施“保增长”的同时也要重视“防通胀”,进而使得经济增速变化和通货膨胀对消费者福利影响保持稳定。

第三,在经济进入新常态导致经济增长率下降的背景下,采取措施阻止居民收入水平从而消费增长率的下降,使居民福利水平不至于大幅度下降。提高居民的收入水平,使居民“能消费”;改善消费环境,使居民“敢消费”;稳定消费预期,使居民“愿消费”。