数据信托下平台数据安全的演化博弈仿真研究
邓 可
(上海政法学院 经济管理学院, 上海 201701)
随着大数据时代的到来,数据安全的重要性日益凸显。互联网平台作为最主要的数据载体,过度收集和滥用用户数据的事件时有发生,不仅侵犯公民的个人信息权益,还对国家安全造成威胁[1-2]。郑婷一等[3]认为平台采用“服务换取数据”的模式,与普通用户力量不对等,形成一种“生态垄断”;丁凤玲[4]认为传统的公民“赋权-维权”模式无法有效约束平台数据权力滥用的行为;范玉吉和张潇[5]、马海群和张涛[6]梳理了我国数据安全治理的特征和行为逻辑,认为构建敏捷的多元治理结构有利于我国数据安全的有序治理。席月民[7]认为数据信托作为一种创新的多方治理模式,在数据安全保护上具有比较优势,越来越多地引起学界的关注。
冉从敬等[8]从制度创新的角度分析,认为数据信托在互联网平台与信托机构之间建立起协作关系,能够在实现多方利益诉求的同时获得数据安全保护的结果;凌超[9]认为理解数据信托有数据治理和数据资产化的双重视角,数据治理是基础,数据资产化是发展方向,无论哪种视角提升数据安全是必要条件;夏义堃等[10]从数据信托的内涵出发,认为数据信托不仅是从法律的角度打破不平衡的权力关系,并且从交易角度解决数据权属、定价、利益分配等问题;黄京磊等[11]研究发现,数据信托最重要的特征是参与者之间的风险隔离,从而使数据信托成为一种可信的数据流通模式;孙宏臣[12]对数据信托的英美两种模式进行了比较分析,指出英美模式在治理结构上的缺陷,并提出数据信托应以“数据出口”规制为重点,建立数据控制人为委托人,信托公司为受托人,数据财产权为标的,第三方专业机构负责生产数据产品的新框架。综上所述,学者们一致认为数据信托兼有个人数据保护和释放数据价值两个方面的功能,并对数据信托的内涵、生成逻辑与实现路径进行了详细阐述,同时有关数据信托的实践研究还处在探索阶段,特别是针对多方治理逻辑下参与各方的协作研究还比较少。邓可[13-14]以博弈论为工具,探讨了数据信托参与者的静态均衡、合作条件和利益分配等问题,具有一定理论价值,但动态条件下的协作研究没有展开讨论。在政府监管环境下,以数据信托为依托规制平台数据安全行为,可以看作一个动态演化过程。平台与信托双方通过不断适应和学习,选择较优的策略,逐步达到系统演化稳定状态。由于决策者的有限理性和决策环境的不确定性,平台以高标准履行数据安全保障义务能否成为信托参与治理下的演化结果非常值得研究。因此,本文探讨数据信托下平台与信托之间的数据安全治理合作问题,同时考虑政府在其中的作用,通过构建演化博弈模型分析双方的动态行为策略,采用MATLAB仿真探究平台与信托履行数据安全保障义务的条件,并提出针对性的建议。
1 演化博弈模型构建
1.1 信托运行原理
在数据信托场景下,所涉及的参与者包括用户、平台、信托、投资人和政府。其运行机制可以表述如下:第一,平台通过其提供的软件服务获得用户数据,并对数据进行脱敏和不可逆处理形成匿名数据,平台则作为实际上的委托人;第二,数据信托项目作为一种专门投资于数据资产的信托产品由信托机构设计并发行,信托机构作为数据信托产品的受托人,代表用户对个人数据的使用进行监督;第三,数据信托的委托人同时也是受益人,收益主要来自项目运营或数据交易,参照公募基金的管理办法,收益的大部分将用于分红;第四,投资人将资金投资于数据信托产品,并根据其投资额参与信托产品的收益分配;第五,政府拥有审核、准入、奖惩、监督、跟踪追溯等权力。由此形成基于数据信托的数据安全保护与治理体系(图1)。
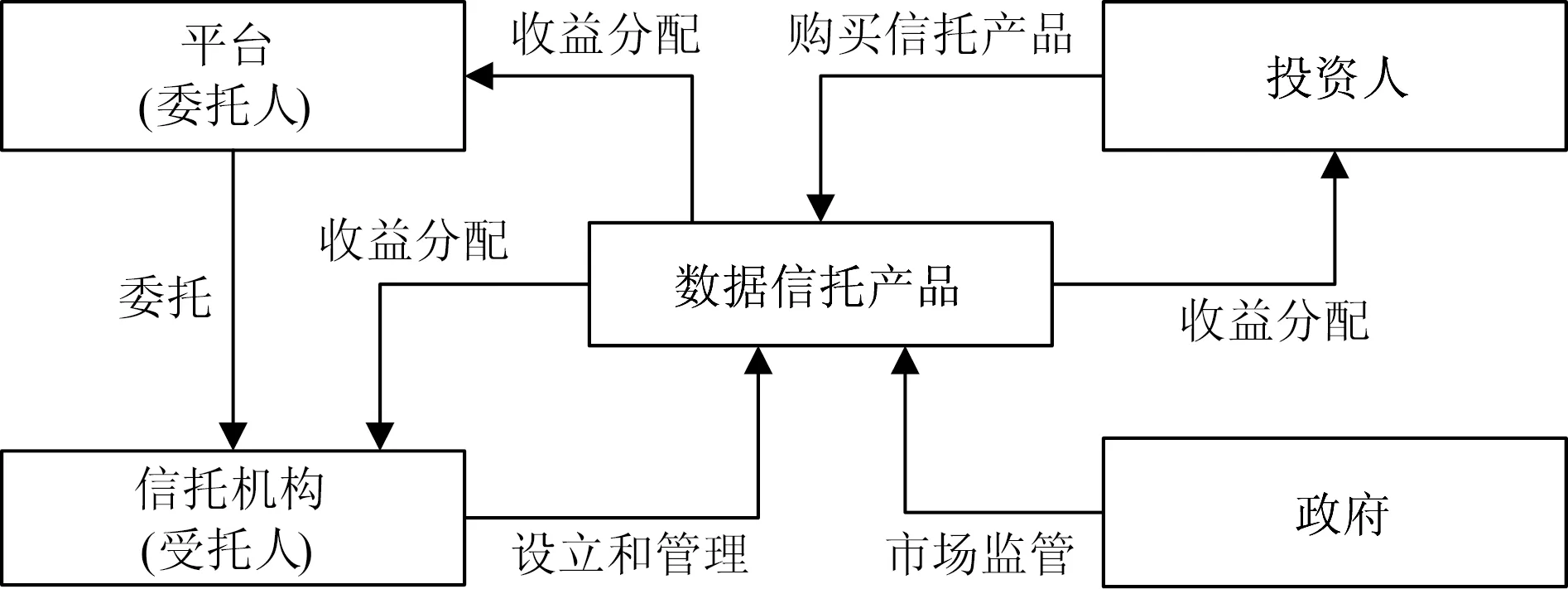
图1 数据信托的运行机制
1.2 模型基本假设
根据数据信托的运行机制,进一步探讨各参与主体的行为。由于一般用户或投资人对于数据安全的作用比较小,不作为研究对象,重点分析平台和信托在履行数据安全保障义务方面的投入行为,同时考虑政府的参与调节功能。模型基本假设如下。
假设1:该演化博弈的参与者分别为信托F和平台E,其策略空间为(遵循高安全标准,遵循低安全标准),博弈双方遵循有限理性原则。在群体F中,选择遵循高安全标准的比例为x;在群体E中,选择遵循高安全标准的比例为y。信托对数据安全投资If,获得数据安全投资收益(Rf-If)。平台对数据安全投资Ie,获得数据安全投资收益(Re-Ie)。
假设2:政府主要利用政策工具调节数据信托项目的安全保护力度。信托和平台遵循高安全标准的情况下,政府对信托的税收优惠为ω(ω≥0),政府对企业的补贴为φ(φ≥0)。信托和平台遵循低安全标准的情况下,政府对信托和平台的罚款基准为L(L≥0),可以根据实际情况调整处罚强度,设定信托的惩罚系数为α(0≤α≤1),平台的惩罚系数为β(0≤β≤1)。
假设3:数据信托项目由信托与平台“收益共享、投资共担”。设定信托对于平台的收入让渡比例为λ(0≤λ≤1),平台对于信托的投资分担比例为μ(0≤μ≤1),则有(Re=λRf,Ie=μIf)。
假设4:在一方遵循高安全标准,另一方遵循低安全标准的情况下,存在溢出效应,设定信托的溢出系数为η(0≤η≤1),平台的溢出系数为θ(0≤θ≤1)。当平台选择低安全标准时,信托需要增加额外的安全投入Ih,而信托选择低安全标准时,平台无法获得信托的收入让渡Re(Re=λRf)。
基于上述假设,建立双方静态博弈的支付矩阵如表1所示。

表1 静态博弈的支付矩阵
1.3 复制者动态方程
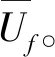
Uf1=y(Rf-If+ω)+(1-y)×
(Rf-If-Ih+ω)
(1)
Uf2=y(ηRf-αL)+(1-y)(-αL)
(2)
(3)
由此构建信托的复制者动态方程F(x),其中Gf(y)为群体策略比例y的函数,且当Gf(y)=0时,y=y*。
x(1-x)(Uf1-Uf2)=x(1-x)Gf(y)
(4)
Gf(y)=y(1-η)Rf-If-(1-y)Ih+ω+αL
(5)

Ue1=x(Re-Ie+φ)+(1-x)(-Ie+φ)
(6)
Ue2=x(θRe-βL)+(1-x)(-βL)
(7)
(8)
平台的复制者动态方程F(y),其中Ge(x)为群体策略比例x的函数,且当Ge(x)=0时,x=x*。
y(1-y)(Ue1-Ue2)=y(1-y)Ge(x)
(9)
Ge(x)=x(1-θ)Re-Ie+φ+βL
(10)
令F(x)=0,F(y)=0,求解该动态演化博弈的局部驻点,得到5个驻点,分别为O(0,0)、U(0,1)、V(1,0)、W(1,1)、S(x*,y*)。
1.4 均衡稳定性分析
根据微分方程的稳定性定理,利用雅克比矩阵进行演化博弈的稳定策略(ESS)分析,对微分方程分别求x和y的偏导数,得到雅克比矩阵为J。将5个驻点代入雅克比矩阵,如果满足行列式detJ为正,行列式的迹trJ为负,则是稳定点。
(11)
首先讨论Gf(0)、Gf(1)、Ge(0)、Ge(1)的正负性。根据式(5),Gf(0)=-If-Ih+ω+αL,由于政府的奖惩激励不能替代信托的投资,否则信托机构会产生投机行为使得政府调节失灵,因此需要满足ω+αL≤If,所以Gf(0)≤0。Gf(1)=(1-η)Rf-If+ω+αL;由于溢出效应需要小于正常投资收益,否则“搭便车”将成为每家信托机构的最优选择,因此需要满足ηRf≤Rf-If,所以Gf(1)≥0。
同理,Ge(0)=-Ie+φ+βL,为避免平台的投机行为,有φ+βL≤Ie,则Ge(0)≤0。Ge(1)=(1-θ)Re-Ie+φ+βL,为避免平台的“搭便车”行为,有θRe≤Re-Ie,则Ge(1)≥0。
在此基础上进行演化博弈稳定状态分析,判断结果如表2所示。
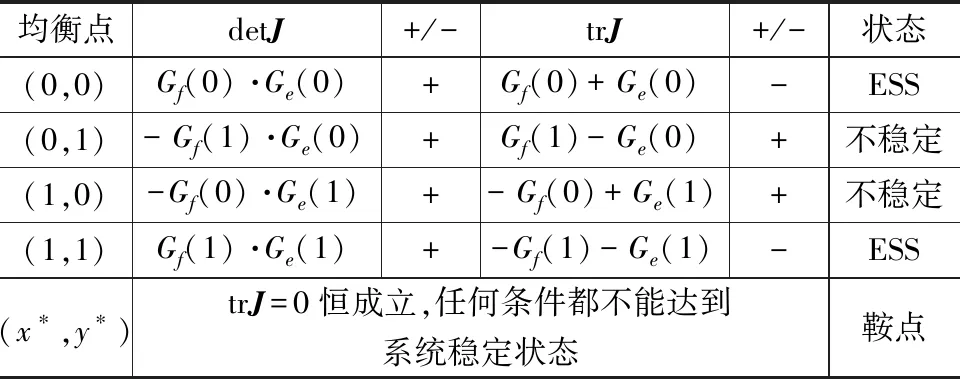
表2 演化博弈稳定状态分析
2 演化博弈系统仿真
为讨论方便且不失一般性,采用参数形式重写复制者动态方程。设定信托安全投资收益率为rf,则Rf=(1+rf)If,信托以百分比rh增加额外的安全投入Ih=rhIf,设定If=L=1。由此,复制者动态方程的参数形式可以表示为
Fn(x)=x(1-x)[y(1-η)(1+rf)-
(1-y)rh+ω+α-1]
(12)
Fn(y)=y(1-y)[x(1-θ)(1+rf)λ-μ+φ+β]
(13)
可得驻点S(x*,y*)有
(14)
满足约束条件:
φ+β≤μ≤(1-θ)(1+rf)λ+φ+β;
ω+α≤1≤(1-η)(1+rf);
ω 进一步采用MATLAB仿真对模型进行分析,在满足约束条件下,各个参数的初值设定如表3所示。 表3 参数初值及含义 根据表3的参数,可以计算演化博弈的鞍点S(x*,y*)=(0.370,0.531),由此初始的群体策略选择比例可以参照该点设置。如果设定值更靠近(1,1),演化博弈趋向于双方(高标准,高标准)的稳定结果;如果设定值更靠近(0,0),演化博弈趋向于双方(低标准,低标准)的稳定结果。此外,信托相对于平台更快收敛于ESS点(图2)。 图2 仿真试验结果分析1 当将(x*,y*) 的初始值固定于(0.370,0.531)时,改变初始参数的设定,将得到不同的仿真试验结果。考虑参数的5种效应对仿真结果的影响,分别是投资效应(rf、rh)、分担效应(μ、λ)、奖励效应(ω、φ)、惩罚效应(α、β)和溢出效应(η、θ)。 如图3所示,投资收益率对系统收敛结果有直接影响,如果项目投资能带来比较高的回报(如rf=0.6),对信托和平台的安全投入有很好的激励作用,博弈双方趋向于选择高安全标准。相对收益率,额外的投资系数提高(如rh=0.3),信托机构会跟从平台选择低安全标准。此外,安全收入的让渡比例以及投资的共担比例,将对平台的安全控制意愿产生重大影响。当让渡比例不变、分担比例提高时,如μ=0.3且λ=0.1,由于过重的投资负担平台将逐渐失去安全控制的意愿,选择高安全标准的平台比例急速下降;相反,当分担比例不变、让渡比例提高时,如μ=0.25且λ=0.2,平台以较快的速度实现理想稳定状态。 图3 仿真试验结果分析2 如图4所示,政府监管对平台和信托有调节作用,加大奖惩力度能够使系统以更快的速度收敛于理想的演化稳定状态,并且惩罚的作用影响更大,对信托进行奖励、对平台进行惩罚能够加快收敛速度。当溢出效应较强时,如η=0.2且θ=0.2,群体存在“搭便车”的行为,系统将收敛于双方均采纳低安全标准的不良状态,而随着溢出效应减弱,双方的投入意愿增强,收敛于良好状态的可能性增加。 图4 仿真试验结果分析3 大数据时代数据产业化发展势在必行,平台数据安全不仅关系到个人隐私保护,同时也是数据要素流通的前提。本文探讨基于数据信托项目构建可行的多方治理路径,促进平台数据安全保护。 数据信托作为一种多方参与的数据治理模式对平台数据安全有积极作用。数据信托引入信托第三方与平台合作,形成数据安全投资“收益共享、投资共担”的局面,能够以市场的方式改变平台对用户数据一家独大的垄断地位,增加平台的数据安全投入和更好地履行数据安全保护责任。 平台在数据安全建设方面投入动力不足的原因在于,数据产权不清,数据安全所需的投资额度较大,缺乏获得投资回报的途径。数据信托将信托机制与数据治理相互结合,利用信托制度的双重所有权结构,将个人数据作为资产的复合权利情形,解决了数据资产的授权使用问题。并且,数据信托产品可以在数据要素市场内流通,吸收投资人的资金解决资金短缺的问题,好的数据信托项目必然能够获得丰厚的投资收益。 平台与信托之间的相互作用至关重要。仿真结果表明,当信托的利益让渡比例增加,平台的安全投入积极性将得到极大鼓励;反之,当平台的投资共担比例提高,其安全投入的意愿将降低。纵然在短期内由于数据安全的相对收益率增加,信托选择高安全标准的比例有所上升,但长期来看由于选择高安全标准的平台比例下滑,额外投资将造成更多的信托选择低安全标准策略。因此,加强平台与信托的共生性合作,通过公平的利益分配和投资共担机制,维护平台的优质数据产品供给意愿,能够有效推动双方达到理想均衡。 市场环境下,平台与信托在初始条件下选择高安全标准的比例越高,将对演化博弈最终到达良性的稳定状态产生重大影响。因此,转换政府的职能非常重要。政府由平台数据安全的直接监管者转型为市场的“守门人”,监管由单一治理模式转型为综合治理模式,通过营造健康公平的市场环境,加强数据信托项目安全生产方面的教育,并且合理利用政策工具,督促平台与信托切实履行数据安全责任。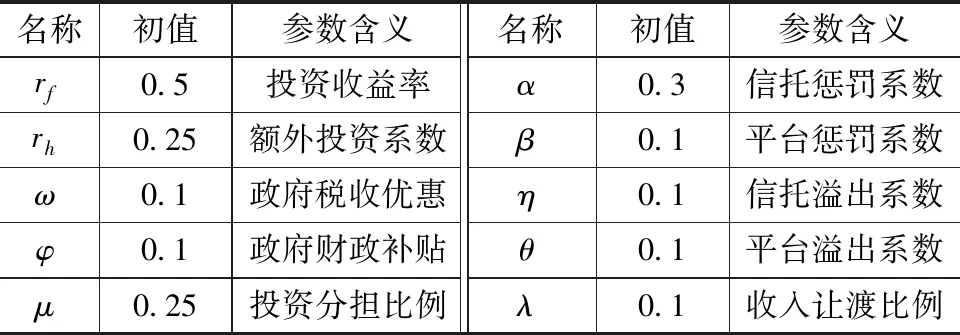
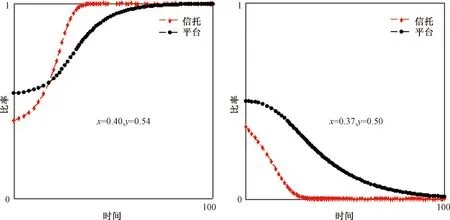
3 结论

