土体液塑限联合测定法及界限含水率相关性分析

高明亮，杨义辉

(1.北京九通衢检测技术股份有限公司，北京 100071；2.重庆公共运输职业学院，重庆 402247 )

1 引言

液塑限是公路土工试验中的一项基本试验， 根据所测的含水率、液限、塑限等界限含水率，计算塑性指数，并根据塑性图利用塑性指数和液限分类对细粒土进行定名[1]。国内外学者关于液塑限试验的研究取得了很多成果，如蒋佰坤等[2]通过试验说明了利用联合测定法的先进性；曹学禹[3]研究了圆锥入土深度在不同材料土体中液塑限的相关性不同；杨婷等[4]运用将最小二乘数法引入液、塑限计算；薛凯喜等[5]研究了竖向渗透分层取样条件下干密度与液塑限的关系；郑德平[6]基于高液限土界限含水率的测定，掺砂改良了路基填料；陈晋[7]通过全自动水分测定仪研究了取样量对测定结果的影响； 陈玉燕等[8]运用数值模拟研究了界限含水率与温度场的相关性；郝志宁[9]将液塑限试验用在了填料选择中， 实现了其在工程施工中的应用。

为深入研究液塑限测定方法及含水率、液限、塑限等之间的相关关系，本文以成资渝高速公路TJ2 标项目为背景，在液塑限联合测试试验的基础上， 对界限含水率的相关性进行研究，拓宽了其在工程领域中的应用。

2 试验原理

液塑限联合测定法，在我国工程建设领域应用较广泛。 根据极限平衡理论，当土中含水率达到液限时，土体处于从黏滞液体状态过渡到黏滞塑性状态的临界点， 试样达到最小抗剪强度[10]。 试锥进入土体深度如图1所示。

图1 液塑限联合测定仪试锥入土示意图

土样接触面与试锥的极限剪应力τ 为：

由式（1）和式（2）得：

将式（3）写成对数形式，则得：

土的无侧限抗压强度与含水率w 的双对数关系，即：

由式（4）和式（6）得：

可见，锥体入土深度与含水率呈对数线性关系。 因此，可根据式（7）求出土样对应的锥体下沉时的界限含水率。

3 工程试验

3.1 试验方案

土样选自于成资渝高速公路TJ2 标项目K61+126～K67+500 段，包含黏土、淤泥质黏土、淤泥质壤土3 类，其中淤泥质土层含水率较高，土质不均匀。

试验仪器为LP-100D 数显式土壤液塑限联合测定仪，试锥质量100 g，锥角30°。盛土杯直径50 mm，高度40 mm，电子天平最大量程500 g， 最小感量0.01 g。 试验严格按照JTG E40—2007 《公路土工试验规程》（本项目建设期为2018—2020 年）中的相关规定进行。

3.2 试验结果

液塑限界限含水率的确定方法主要包括回归法、作图法、最小二乘法、解析法等。运用液塑限联合测定仪，采用100 g 试锥时，根据规范中含水率与锥入深度的双对数坐标，查出试锥入土深度h=20 mm 所对应的含水率即为液限；液限与塑限入土深度关系图中，查找塑限。 本试验所测20 组土体液塑限，结果如表1 所示。

表1 液塑限联合测定试验结果

4 相关性分析

4.1 天然含水率与液限相关性、天然含水率与塑限相关性

为进一步分析天然含水率与液限、塑限相关性，选取表1试验结果中的20 组作为样本，运用EXCEL 函数进行拟合。结果显示，含水率与液限、塑限相关性较好，可拟合为一次函数以及二次函数，如图2 和图3 所示。

图2 含水率与液限、塑限一次函数拟合

图3 含水率与液限、塑限二次函数拟合

4.2 液限与塑限相关性

同样选取表1 试验结果中的20 组作为样本，以液限作为横坐标、塑限作为纵坐标，运用EXCEL 函数进行拟合，得到液限与塑限的拟合函数如图4 所示。

图4 液限与塑限线性关系拟合

4.3 拟合函数检验及误差分析

为验证比较采用含水率与液限、塑限拟合函数的精确度，别取10 组土样验证，分别测试，并用图2、图3 所示函数关系进行计算，用作对比，结果如表2 所示。

表2 液塑限联合测定试验与拟合计算对比

从表2 的计算结果，可以看出，土的含水率与液限、塑限呈现一次函数关系和二次函数关系，难以确定，因此需要进行误差分析。 即分析拟合计算结果与实测值的相对误差的绝对值。 如表3 所示。

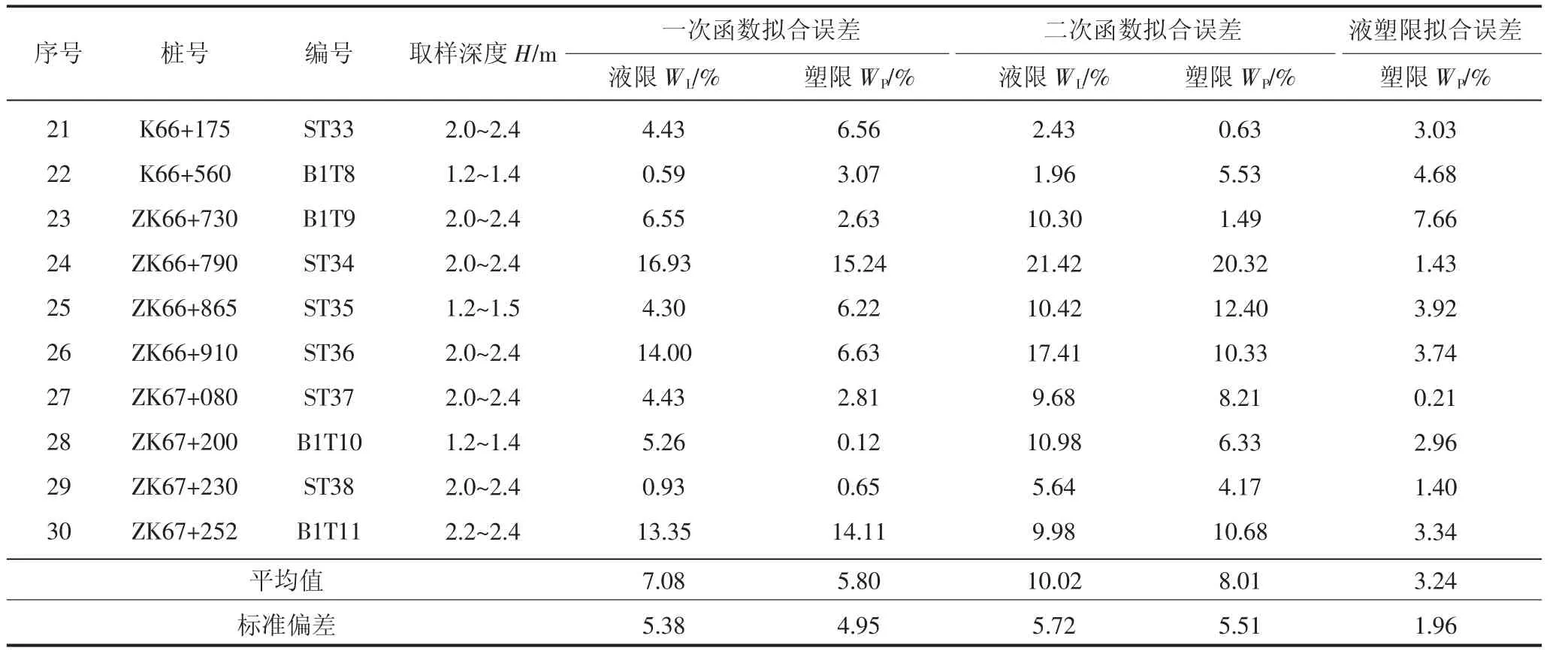
表3 液塑限联合测定试验与拟合计算误差分析表

从误差分析表可以看出，对于土的含水率与液限、塑限之间的相关性拟合为一次函数其误差平均值和标准偏差更小，10 组验证土样的误差分布如图5 所示。 该研究结论与一些学者的研究结论相吻合，与实际更为接近。

图5 用于验证的10 组土样拟合函数相对误差分布图

土的含水率与液限的函数关系式为：WL=0.732 7W+23.268，与液限的函数关系式为：WL=0.309 9W+15.575。 液限与塑限的函数关系式为：WP=0.379 3WL+7.515 7。

5 结论

本文研究了液塑限联合测定法的试验原理， 依托工程项目， 基于液塑限联合测定法对不同测点入土深度范围的液塑限进行了测试， 并根据测试结果对各界限含水率之间的相关性进行了分析，得到如下结论：

1）对液、塑限联合测定法试验原理进行了研究，得出了锥体入土深度与其含水率呈对数线性相关的结论。

2）所选工程项目土体的含水率与液限之间可拟合为一次函数，相关系数为：R2=0.580 2；亦可拟合为二次函数，相关系数为：R2=0.704 4。 含水率与塑限之间可拟合为一次函数，相关系数为：R2=0.565 2；亦可拟合为二次函数，相关系数为：R2=0.793 5。

3）液限塑限之间同样具有较好的相关性，可拟合为一次函数，相关系数为：R2=0.783 6。

4）从误差分析表可以看出，对于土的含水率与液限、塑限之间的相关性拟合为一次函数其误差平均值和标准偏差更小，与实际更为接近。