广义(2+1)维Zakharov-Kuznetsov方程的精确解

华 瑞，王振立，孙亮吉

(枣庄学院 数学与统计学院，山东 枣庄 277160)

0 引言

在数学、物理、光纤孤子通信以及计算机工程技术等领域中经常会涉及到许多非线性现象，这些现象大多可用非线性发展方程来描述。一直以来，非线性发展方程的求解问题都是数学和物理学家研究的重要课题之一，特别是研究非线性发展方程的精确解，其研究成果对解释许多物理现象及工程应用起着重要的指导意义。为了得到非线性发展方程的精确解，许多有效方法，如经典和非经典的李群方法[1-6]、雅可比椭圆函数方法[7-9]、广义的tanh函数法[10-11]、广义的代数法[12]等已经被提出。其中广义代数法是最重要的方法之一，本文是利用广义代数法考虑广义(2+1)维Zakharov-Kuznetsov(简称ZK)方程[13]的精确解，在文献[14]中运用了扩展的(G′/G)方法求得ZK方程的精确解，本文是在此基础上将精确解进一步推广。

ut+aux+bupux+cuxxx+euxyy=0，p>0

(1)

式中：a、b、c、e是任意非零常数。当p=1时，方程(1)就化为(2+1)维Zakharov-Kuznetsov方程。20世纪80年代末，Zakharov和Kuznetsov在描述磁化等离子体德尔演化过程中首次导出该模型，也就是说ZK方程是最早描述非线性离子声波的模型，ZK方程是著名的KdV方程在二维空间的推广形式，是应用渐进多尺度技术在磁场中发现的一种磁等离子波，在物理领域内有着广泛的应用。

1 广义代数法概述

考虑如下偏微分方程

F(u，ux，ut，uxx，uxt，utt，……)=0，

(2)

u(x，t)是未知函数，F是关于u及其偏导数的已知多项式。广义代数法的应用步骤包括：

第1步，作行波变换。令u(x，t)=u(ξ)，ξ=kx+lt则式(1)就变为一个关于u=u(ξ)的常微分方程，

p(u，ku′，lu″，k2u″，klu″，l2u″，……)=0。

(3)

第2步，假设式(3)有下述形式的解：

u(ξ)=amφm+am-1φm-1+……+a0，am≠0，

(4)

关于φ的项共有m+1项，这里的φ满足：

(5)

由方程(5)可以得到：φ′、φ″、φ‴、…的表达式，平衡式(3)中的最高阶导数项与最高阶非线性项的次数确定m的值。

第3步，确定超定方程组。把φ′、φ″、φ‴、…的表达式代入到式(3)中，令φ各项的系数为零，得到关于ai的代数方程组P=0。

第4步，确定精确解，求解代数方程组P=0，得到式(3)的行波解。

2 广义(2+1)维Zakharov-Kuznetsov方程的精确解

作行波变换，u(x，t)=u(ξ)，其中ξ=x+ky+lt，带入方程(1)得到

(a+l)u′+bupu′+(c+ek2)u‴=0，

(6)

其中：k和l是任意常数。平衡upu′和u‴，得到pn+n+1=n+3，故有n=2/p。

令

(7)

把式(7)带入方程(6)得

(8)

即

(a+l)p2f2f′+bp2f4f′+(c+ek2)[2(p2+3p-2)f′3-

p(3p-6)ff′f″+p2f2f‴]=0。

(9)

显然，方程(9)是一个常微分方程，求解方程(9)要比求解方程(1)简单的多。

在方程(9)中，平衡f2f‴和f4f′，得到m=1。假设方程(9)有如下形式的解

f(ξ)=q1φ(ξ)+q0，q1≠0，

(10)

其中：qi(i=0，1)是需要确定的常数。φ(ξ)满足下面的常微分方程

(11)

其中：ε=±1，hj(j=0，1，…，n)是任意常数。取n=4，由方程(11)得

(12)

由方程(12)得到

φ′2=h0+h1φ+h2φ2+h3φ3+h4φ4，

(13)

(14)

φ‴=φ′(h2+3h3φ+6h4φ2)，

(15)

φ′3=φ′(h0+h1φ+h2φ2+h3φ3+h4φ4)。

(16)

把方程(13～16)和方程(10)代入方程(9)得到一个关于φ的代数的代数方程组，令相同次幂的φ的系数为0，得到一系列代数方程组，解得：

其中：p是任意正常数。h0，h2和h4取不同的值，可以得到方程(9)的大量的解，结合式(7)可以得到方程(1)解如下：

情况1：有理函数解

当h0=h2=0时，得到方程(1)的有理函数解：

情况2：雅可比椭圆函数解和混合椭圆函数解

当h2=-(1+m2)时，得到方程(1)的四个椭圆函数解：

当h2=1-2m2/2时，得到方程(1)的五个混合椭圆函数解：

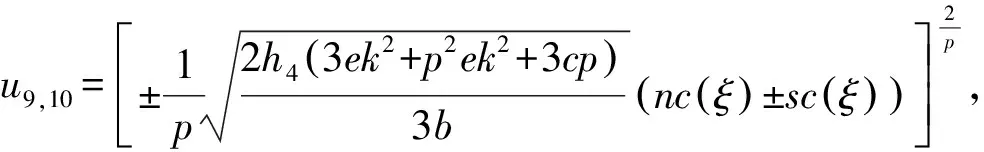
为了直观地显示精确解的性质，绘出有理函数解的参数值分别为h4=1、c=a=b=e=k=1、t=0和雅可比椭圆函数解的参数值分别为h0=0、h4=1/4、c=a=b=e=k=1、t=0的三维空间波形图，如图1、2所示。

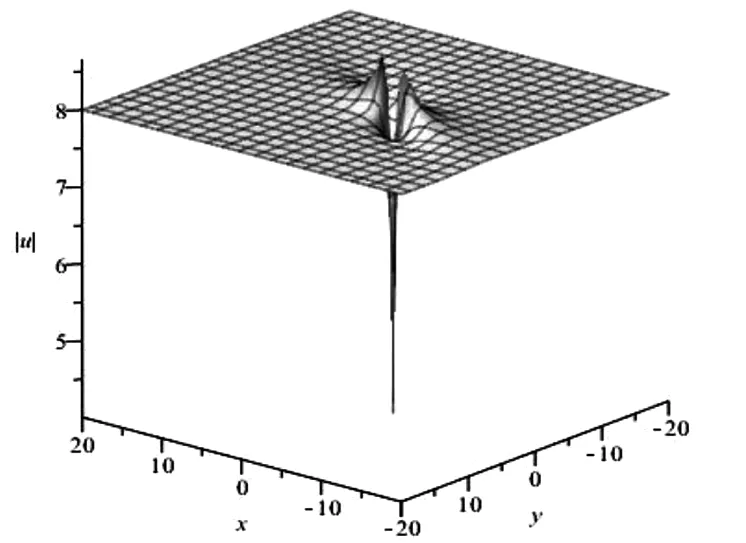
图1 有理函数解的波形图

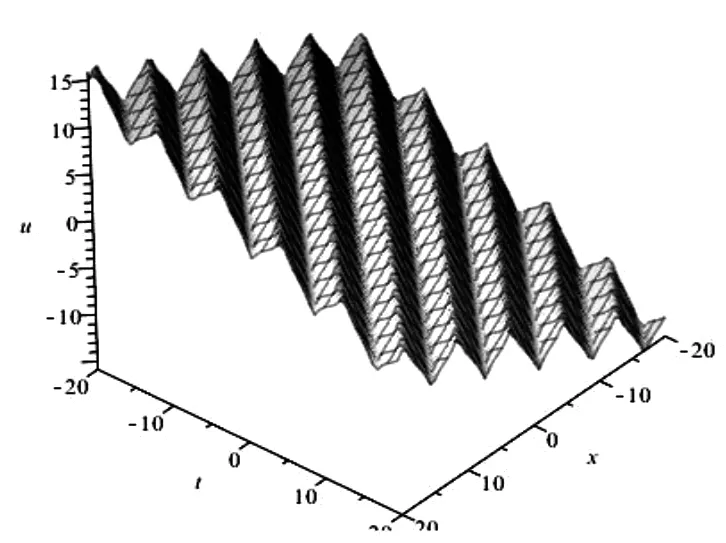
图2 雅可比椭圆函数解的波形图

情况3：扭结解

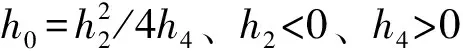
情况4：奇异解

当h0=0、h2>0、h4>0时，得到方程(1)的一个奇异解：

为了直观地显示精确解的性质，给出了扭结解的参数值分别为h2=-1、h4=1、c=a=b=e=k=1、t=0和奇异解的参数值分别为h2=h4=c=a=b=e=k=1、t=0的三维空间波形图，如图3、4所示。

图3 扭结解的波形图

图4 奇异解的波形图

情况5：三角函数解

当h0=0、h2<0、h4>0时，得到方程(1)的两个三角函数解：

为了直观地显示精确解的性质，绘出了三角函数解的参数值分别为h2=-4、h4=1、c=a=b=e=k=1、t=0的三维空间波形图，如图5所示。

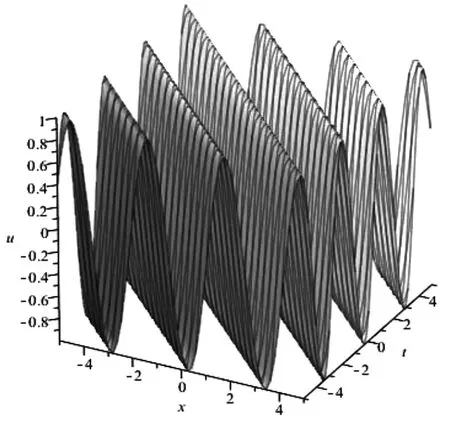
图5 三角函数解的波形图

注：解u1～u6在文献[14～16]中均有出现；但是u7～u15都是新的精确解，是前面求的解u1～u6的推广；

3 结论

本文利用广义代数法，研究广义(2+1)维Zakharov-Kuznetsov方程，得到了该方程的新的精确解，这些解包括有理函数解、雅可比椭圆函数解、混合椭圆函数解、扭结解、奇异解、三角函数解等。通过绘出精确解三维空间波形图更能直观地了解该精确解的性质，这些精确解对解释复杂的物理现象(含有冷离子和热等温电子的磁化等离子体中的平面波的传播)有重要的作用，同时广义代数法也适用于其它类型的非线性发展方程，对于求解变系数方程也有较好的应用。