基于深度范围选取的单光子激光雷达高效率图像重建算法
孟凡星,张同意,康岩,薛瑞凯,王晓芳,李薇薇,李力飞
(1 中国科学院西安光学精密机械研究所 瞬态光学与光子技术国家重点实验室,西安 710119)
(2 中国科学院大学,北京 100049)
0 引言
主动光学成像系统凭借自身的照明可在夜晚、水下、浓雾等低照度环境下实现目标探测,更重要的是其可获得目标的距离信息,譬如三维成像激光雷达。相比于被动成像系统具有更强的鲁棒性和全天时成像能力,广泛应用于遥感测绘、生物医学成像、城市建模等领域[1-5]。光子计数激光雷达三维成像技术是一种新型主动成像激光雷达技术,具有单光子的探测灵敏度,与时间相关单光子计数(Time-correlated Single-photon Counting,TCSPC)技术结合能实现皮秒的高时间分辨率,从而进行高距离分辨率三维成像[6-11]。时间相关单光子计数激光雷达的传统工作方式是通过向目标重复发射激光脉冲,探测每个激光脉冲反射回来的光子并进行计数累积。当目标的每个像素点都累积成千上万回波光子后,可以抑制背景噪声光子和探测器暗计数的不利影响,降低光子飞行时间抖动带来的距离不确定性,测距精度可达毫米甚至微米,从而获得远距离目标的高分辨三维图像。但这种传统的重复测量工作方式需要很长的数据采集时间,限制了其在城市建模、动态目标遥感等的实际应用。在没有足够长的数据采集时间,只获得极少回波光子数据的情况下,如何从低信噪比、极少回波光子的数据重建高精度三维图像成为时间相关单光子计数激光雷达当前亟待解决的问题。
为解决上述问题,2014 年,美国麻省理工学院的KIRMANI A 等[12]提出了首光子成像方法,该方法用激光脉冲逐像素照射目标,每个像素只记录第一个光子计数事件,通过建立首光子的探测概率模型,利用每个像素探测到首个光子前系统所发射的激光脉冲个数,以及所探测光子的飞行时间来重构目标反射率和距离图像,并利用场景相邻像素距离和反射率相近的空间相关性先验知识进行图像降噪与图像平滑处理。首光子成像在每个像素仅仅检测到一个光子的情况下实现了三维成像,相比于通常每个像素需要几十、几百甚至成千上万光子才能成清晰的图像,光子的利用效率大大提升。但首光子成像方式每个像素所需的数据采集时间是不确定的且不同像素所需的时间也不相同,使得该成像算法无法直接应用于采用阵列单光子探测器的系统,因为对于阵列探测器,所有像素的光子收集时间是相同的,但每个像素上的光子计数数目却不同。2015 年SHIN D 等[13]通过修改首光子成像的探测模型,采用逐像素等时扫描工作方式,实现了平均每像素一个光子的高光子效率目标三维重建,并在2016 年实现了基于阵列探测器的平均每像素一个光子的目标三维重建[14]。但首光子三维成像及改进的高光子效率三维成像都仅适用于信噪比不是太低的环境,在信噪比低于1 的情况下对噪声的滤除效果不显著,获得的三维图像质量会较差。针对信噪比低于1 的工作情况,2017 年美国波士顿大学的RAPP J 等[15]提出利用噪声光子到达时间的均匀性和信号光子到达时间的聚集性,通过逐像素自适应设置局域门控的方法进行信号光子和噪声光子分离,并对空缺像素进行邻域像素均值填充,在信噪比低至0.04、平均每像素2 个信号光子的低信噪比少光子条件下重建了目标场景的三维图像。但该算法因为要进行逐像素自适应局域时间窗计算,计算量非常大,图像重构时间太长,难以满足快速成像的要求。
为了进一步提高对低信噪比、极少量回波光子的场景重建效果和速度,提出一种基于全局多深度范围选取的高光子效率重建算法。该方法首先选取场景信号的范围,剔除信号范围外的噪声数据。相较于传统的设置全局单一门控的方法,此过程可以更准确地确定信号范围,尤其适用于探测场景中存在多个不同深度目标的情况;而传统的全局单一门控对于多个不同深度目标的情况必须把不同深度目标全部包含进来,目标之间距离间隔对应的时间段内的背景噪声光子数据也会包含进来,不仅增加了噪声带来的距离估计精度降低,而且无效数据的扩充会增加图像重构的计算时间。然后针对少量回波光子造成的像素空缺问题,自适应地进行邻域补充,相较于固定邻域补充能更好地解决光子稀少的问题。最后,使用总变分(Totalvariation,TV)正则化来去除信号范围内的残余噪声,进一步改善图像质量。仿真和实验验证了所提算法可用于低信噪比、极少量回波光子环境下的三维图像重建。
1 算法原理
图1 为单光子计数激光雷达的工作原理示意。激光器向目标重复发射激光脉冲,从目标表面返回的光子利用光电探测器探测,TCSPC 模块将探测周期等间隔划分为若干个时间片(Time Bin)。根据返回光子到达时刻其统计到不同的时间片内,经过一段重复探测时间后对时间片内的光子个数进行统计,形成光子达到时间分布直方图。通过解算算法从光子达到时间分布直方图获得光子的飞行时间,从而确定系统和目标之间的距离。通过单点扫描或阵列探测方式对每个像素都这样进行大量回波光子累积,获取每个像素的光子飞行时间分布直方图[16-18],进而得到场景每个像素的深度信息,完成场景三维重建。
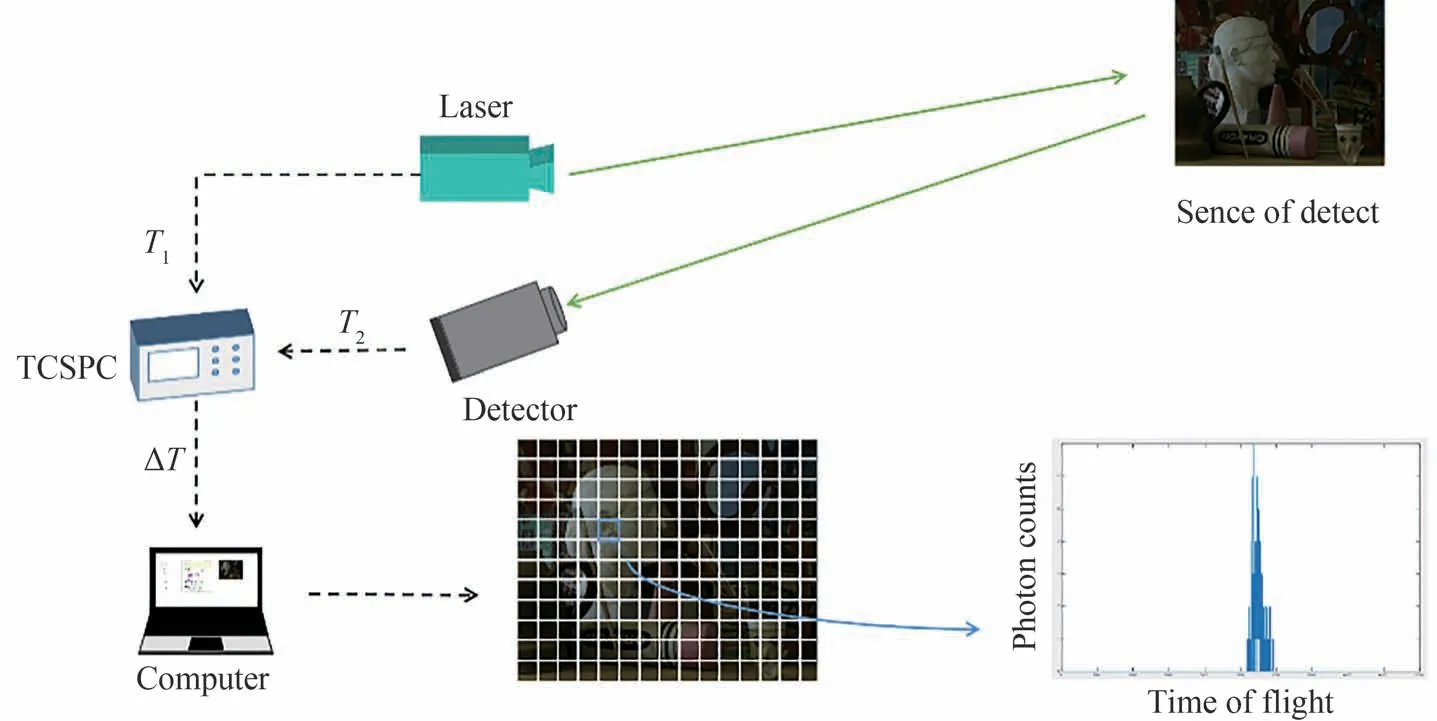
图1 单光子激光雷达成像系统示意Fig. 1 Schematic of a single-photon lidar imaging system
从光子达到时间分布直方图获得光子飞行时间的传统解算方法是将光子到达时间直方图与系统仪器响应函数(Instrument Response Function,IRF)进行互相关计算,也称为匹配滤波算法[19]。但该算法只适用于背景噪声光子较少且回波信号光子充分累积的情况,对于只收集到较少回波光子的情形无法精确重建场景的距离图像。在极少量回波光子和低信噪比的情形下,单个像素典型的光子到达时间直方图如图2,只稀疏地在不同的时间片中存在几个光子探测事件,且有可能这些光子探测事件并非目标的回波光子,而是背景噪声光子引起的。单个像素的光子到达直方图信号聚集性和噪声均匀性不够明显,在这种情况下逐像素进行直方图与IRF 的互相关计算会导致获取的深度信息很不可靠,因而需要研究针对这种情况下的高光子效率图像重构算法。

图2 极少回波光子情形下单个像素典型的光子到达时间直方图Fig. 2 Typical histogram of photon arrival time of single pixel in the case of very few echo photons
为此提出一种基于全局多深度范围选取的高光子效率重建算法。首先把所有像素的光子到达时间数据归并在一起,依靠全部数据形成一个总的光子飞行时间直方图;然后对总直方图进行信号全局距离范围的选取,删除各个像素点中距离范围外的噪声光子,并采用自适应邻域来补充空缺像素及光子较少像素的光子计数;最后使用TV 正则化来平滑残余噪声形成目标的距离和反射率图像。整体算法流程如图3。

图3 整体算法流程Fig. 3 Flowchart of overall algorithm
接着结合一组低信噪比、不同量级回波光子的仿真数据[20]对所提算法进行详细说明,重建效果及与SHIN D[13-14]和RAPP J[15]这两种最新技术处理结果的对比分析在第2 节实验结果部分给出。
1.1 回波光子模型
研究表明弱回波条件下目标回波光子分布满足泊松分布[21-23],用Pi,j(k)表示第(i,j)个像素中一个探测周期T内回波光子数为k的概率,即
式中,λi,j为一个探测周期T内探测器的平均响应数,表示为
式中,η为探测器的量子效率,αi,j为第(i,j)个像素的反射率,f(t)为仪器响应函数,Sν、Sd分别为像素(i,j)中环境光在光学操作频率ν下引起的光通量和探测器暗计数引起的光通量。由于单光子探测器SPAD 存在死时间,对于反射回波脉冲多于一个光子的情况,SPAD 记录到一个光子后,对后续到达的另外几个光子会没有记录。在一个探测周期内,一个有效光电子探测和多个有效光电子探测都只能记录一个脉冲事件,因此在一个探测周期内记录有光子触发事件的概率表示为
这造成了光子的到达概率与光子的探测概率不一致。光子到达时间直方图会向较早时刻偏移,形成所谓的堆积变形,影响距离估计的准确度。为了避免探测器死时间的影响,TCSPC 通常设置成极低通量工作模式,经验法则是使得每发射一个脉冲,记录到光子探测事件的概率低于5%[18,24],即在一个探测周期内检测到一个光子的概率远小于1。因此很多脉冲周期内实际上没有回波光子,偶尔一个脉冲会探测到一个回波光子,而具有一个以上光子的概率几乎为零,低到可以忽略。本文关注的极少量信号回波光子的应用场景正是这种情况,故可不考虑探测器死时间对探测概率的影响,假定光子探测概率与光子到达概率都遵从式(1)的泊松分布。
1.2 深度范围选取
噪声光子具有均匀分布性,偏差较大的噪声直接通过TV 正则化处理会使图像过于平滑。因此,首先进行全局多深度范围选取,把目标场景所占据的一段或几段深度范围选定出来,把这些范围之外所对应的时间片中的光子计数数据删除掉,可在后续处理过程中不被偏差较大的噪声所影响。图4 为深度范围选取的流程,包括所有像素光子探测数据合并形成总直方图,直方图峰值搜索,潜在深度区间确定,深度区间审查,确定有效深度范围五个步骤。
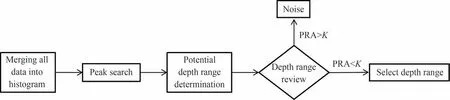
图4 深度范围选取的流程Fig. 4 Flowchart of depth range selection
步骤1:全局总直方图形成。
如前所述,极少回波光子情形下单个像素典型的光子探测事件只稀疏地在不同的时间片中,且有可能这些光子探测事件并非目标的回波光子,而是背景噪声光子引起的。因此不能逐像素单独处理,为此,把所有像素的光子探测事件合并在一起,形成一个全局光子飞行时间的总直方图。由于目标占据有限几段空间,全局累积的结果,可以形成一个多峰的直方图,如图5(a)。
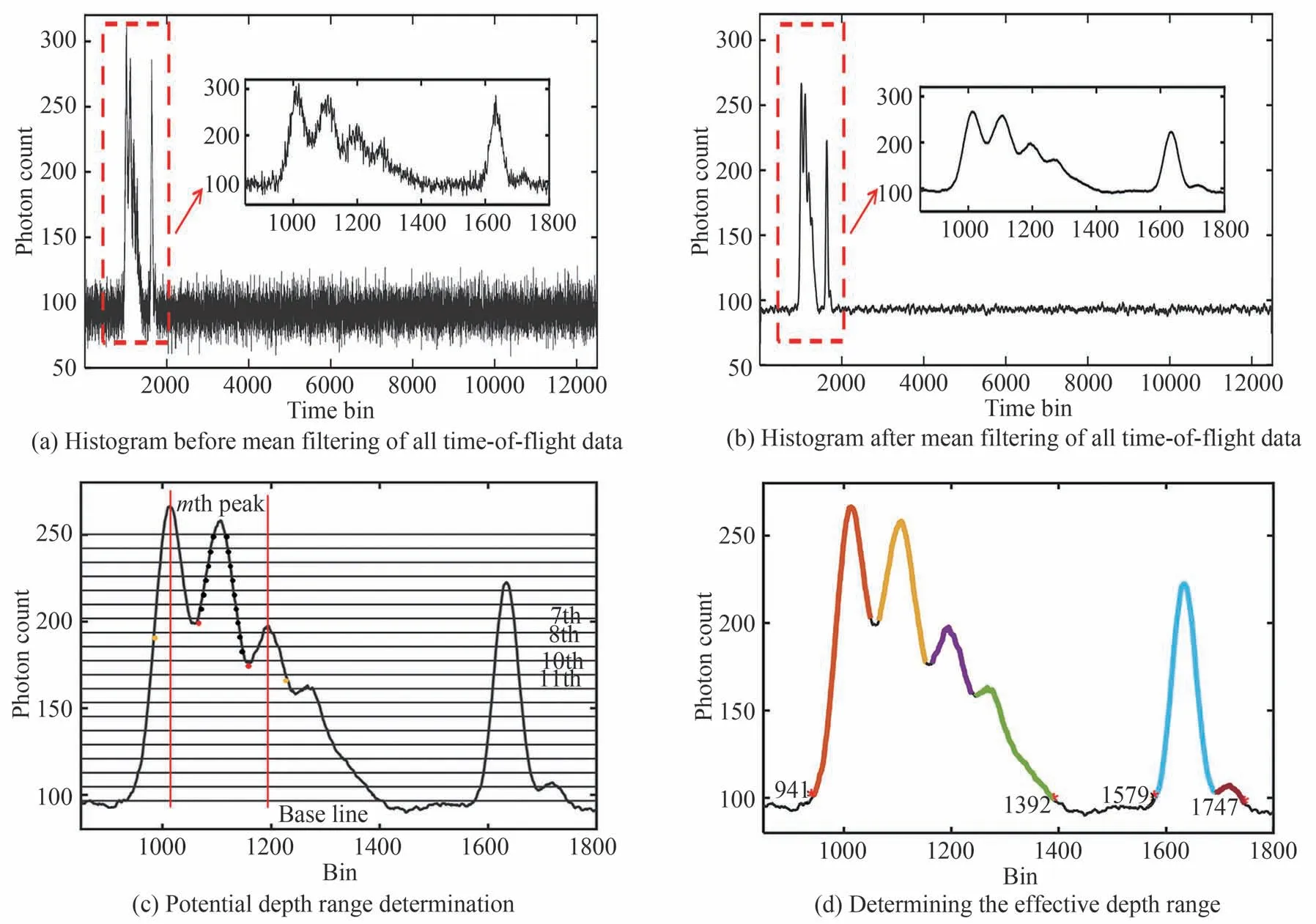
图5 目标场景深度范围选取原理Fig. 5 Schematic of the depth range selection of the target scene
步骤2:直方图峰值搜索。
深度范围需要联合目标的直方图峰值区间来获得,因此首先进行直方图峰值及峰值区间提取。全部数据直方图具有明显波动,为便于提取峰值位置,对直方图进行均值滤波,这可以很大程度上减小直方图波动,但不会造成峰值位置偏移。均值滤波前后对比如图5(a)、(b)。在处理后的直方图上提取M个极值作为峰值点,这是由目标、噪声及内反射等引起的。
步骤3:潜在深度区间确定。
逐个确定每个峰值区间的过程如图5(c)。以第m(m>1)个峰值区间的左界限判断过程为例,第m个峰值与基线之间的高度被N+1 等分(图5(c)中N=19),基线高度通过对直方图求均值获得。从上往下依次寻找小于第n个等分线、分布在峰值左侧,最近的一个点的时间bin 位置,并将这个bin 位置记为sn1。若满足判定条件:第m-1 个峰值在(sn1,binm)区间内,则第m个峰值左界限Lm被确定为上一等分线确定的sn1*。此过程及边界条件由下方的伪代码给出,右界限Rm的判定同理。

步骤4:深度区间审查。
用同样的方法获得以此M个峰值为中心确定的潜在信号区间右界限,为了去掉由噪声(内反射作为噪声处理,但内反射仅在实验数据中存在)引起的峰值以获得目标的深度范围,对M个峰值进行审查。设置参数PRA,定义为所属峰值区间内光子位置标准差(用STD 表示)与所属峰值区间内光子数目NO 的比值,即
对飞行时间数据进行匹配滤波,根据匹配滤波结果计算审查参数。目标区域,STD 和NO 成正比,PRA也较小;噪声均匀分布在整个场景内,STD 大,NO 小,所以PRA 大。因此,通过PRA 可以将噪声和信号有效地区分。对0.04 信噪比、0.3 平均信号光子(Signal Photon Per Pixel, SPPP)的保龄球模拟数据[20]进行参数审查之后可得到表1。其中,NAN 代表STD 为0,即小的噪声波动。SPPP 定义为
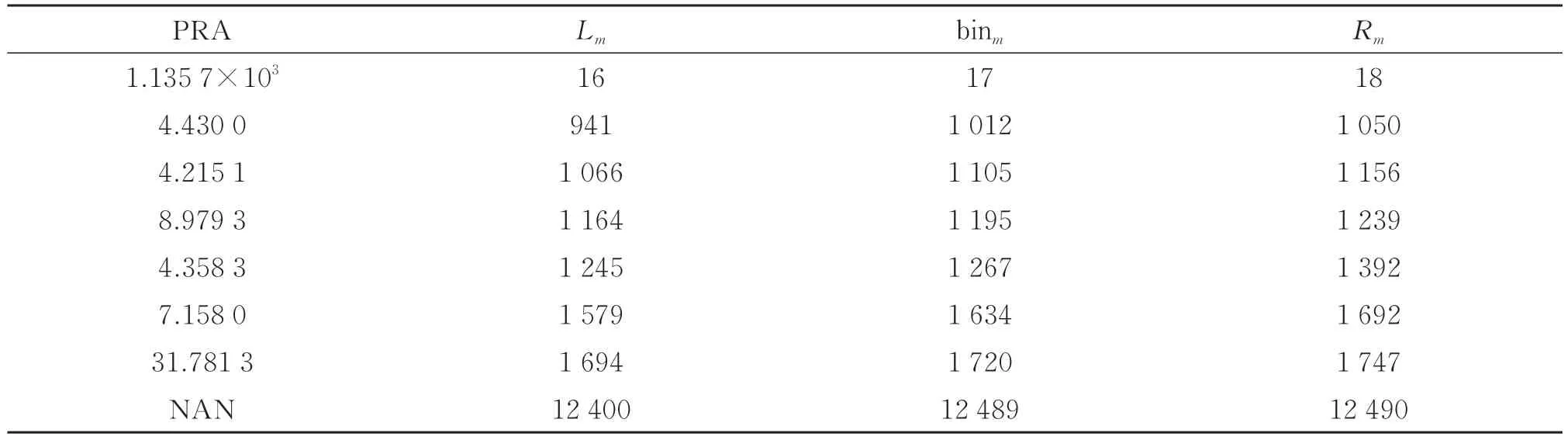
表1 审查参数表Table 1 Review parameter table
式中,Ci,j表示第(i,j)个像素中信号光子的个数,Nr、Nc分别表示图像像素的行数和列数。
步骤5:确定有效深度范围。
对符合要求的峰值区间(表1 中第二行到第七行数据)进行连接,若前一个峰右界限与后一个峰左界限的距离小于阈值,则将两个峰值区间连接起来。否则,不进行连接。最终,获得深度范围如图5(d)。获得深度范围之后,将每个位置的飞行时间数据进行筛选,去除不属于深度范围内的光子,完成光子筛选过程。
1.3 空缺像素自适应补充与图像正则化重建
针对于极少量回波光子环境中存在大面积空白像素,对筛查范围后的飞行时间数据进行自适应邻域补充。如果光子数小于等于X,则不断扩大邻域补充光子,直到邻域光子数大于X。X的值根据经验确定。一般来说,X越大,重建效果越好。然而,当X超过某一阈值时,重建效果将不再改变。仿真数据X取10,实验场景1 中X取40,实验场景2 中X取20。自适应邻域补充的流程如图6,对于像素(i,j),首先进行光子计数,记为Ni,j。如果Ni,j>X,则不进行邻域补充,否则,扩大邻域范围并将以(i,j)为中心的(2ω+1)2个像素的光子作为像素(i,j)的光子,其中,ω=1,2,3,…为扩大邻域的次数。重复此过程,直至(i,j)内的光子计数满足Ni,j>X。传统的局部邻域补充在极少光子环境下仍会存在很多空白像素,因此自适应邻域补充非常必要。
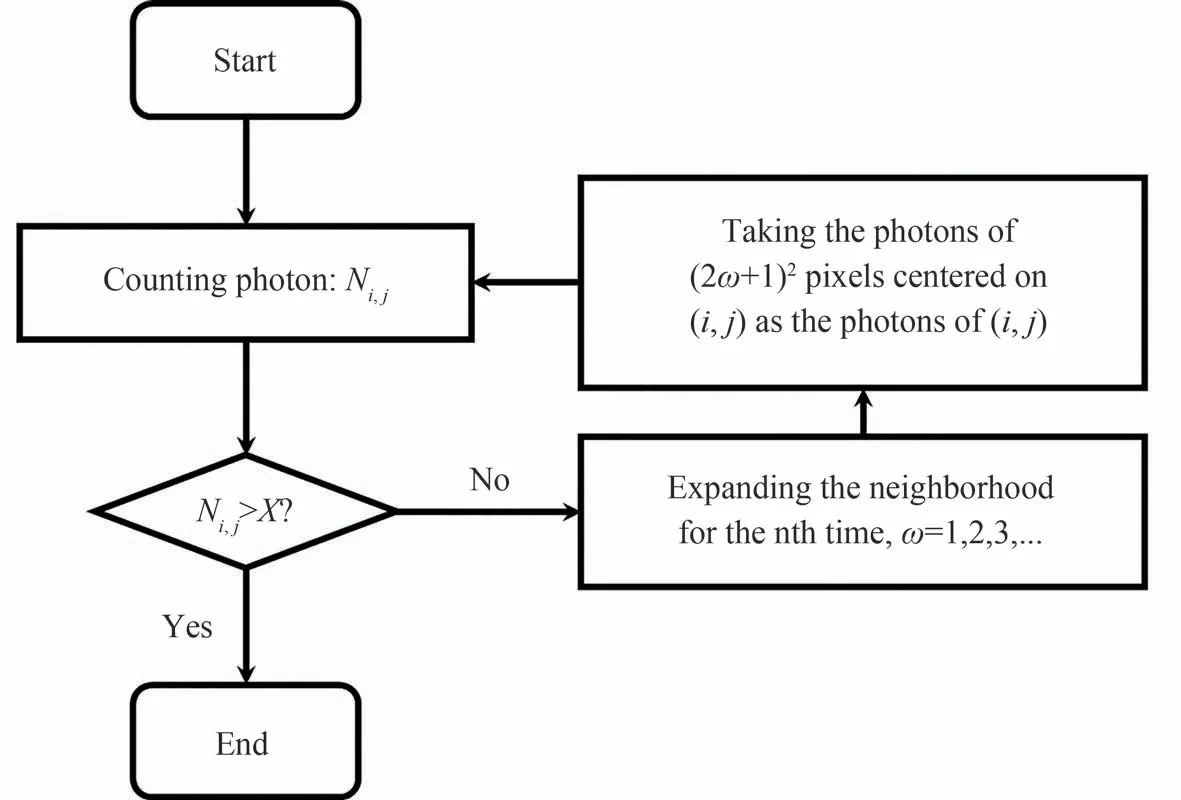
图6 空缺、少光子像素进行自适应邻域光子补充流程Fig. 6 Flowchart of adaptive neighborhood photon supplementation for vacant and few photon pixels
完成空缺像素自适应补充后,通过TV 正则化图像重构过程可以进一步去除残留深度范围内的噪声。带TV 正则项的最小化问题求解表达式为[13]
2 实验结果
2.1 仿真数据验证
为验证所提算法的三维重建能力,通过仿真数据[20]进行了低信噪比、不同量级回波光子的重建,并与SHIN D 等[14]提出的高光子效率算法、RAPP J 等[15]提出的Unmixing 方法进行了对比。将经过所提方法预处理的数据输入到Unmixing 方法中进行处理(Preprocess-unmixing, PP-Unmixing),以验证深度范围选取这一过程的贡献,预处理仅包括深度范围选取。采用信噪比说明仿真条件,信噪比的定义为
即γ个重复探测周期T内探测器对信号的平均响应数与噪声的平均响应数之比。实验中信噪比的测量可如下进行:先关闭照明激光光源,由TCSPC 获得背景光子和探测器暗计数引起的背景噪声计数;然后打开照明激光光源,由TCSPC 获得信号光子与背景噪声计数之和的总光子计数,信号计数由总计数减去噪声计数得出;最后,SBR 用信号计数与背景噪声计数之比给出。用均方根误差(Root Mean Square Error , RMSE)表征重建图像的质量, RMSE 的表达式为
式中,Zi,j是重建后的深度值,Truthi,j是目标真实深度值。表2 为这些重建结果的均方根误差RMSE 和消耗时间。图7 是四种方法在信噪比为0.04 时,对不同SPPP 数据的重建结果。图7 和表2 仅展示部分SPPP 情况下的重建效果。
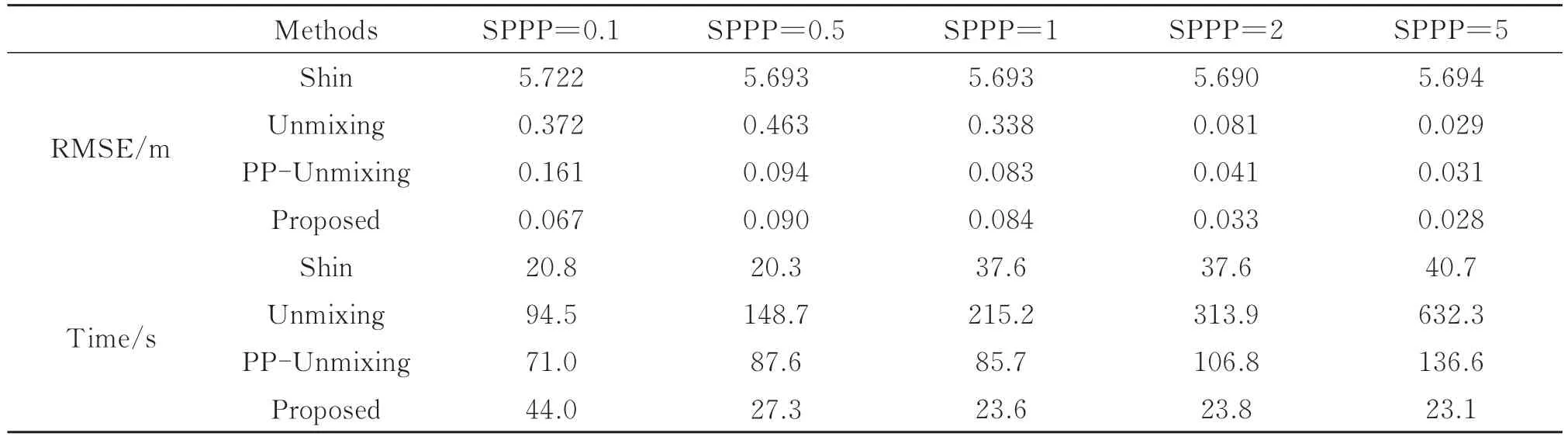
表2 信噪比为0.04 时,四种方法的重建结果随SPPP 变化的均方根误差和消耗时间Table 2 The RMSE and consumption time of the reconstruction results of the four methods vary with various SPPP at SBR=0.04
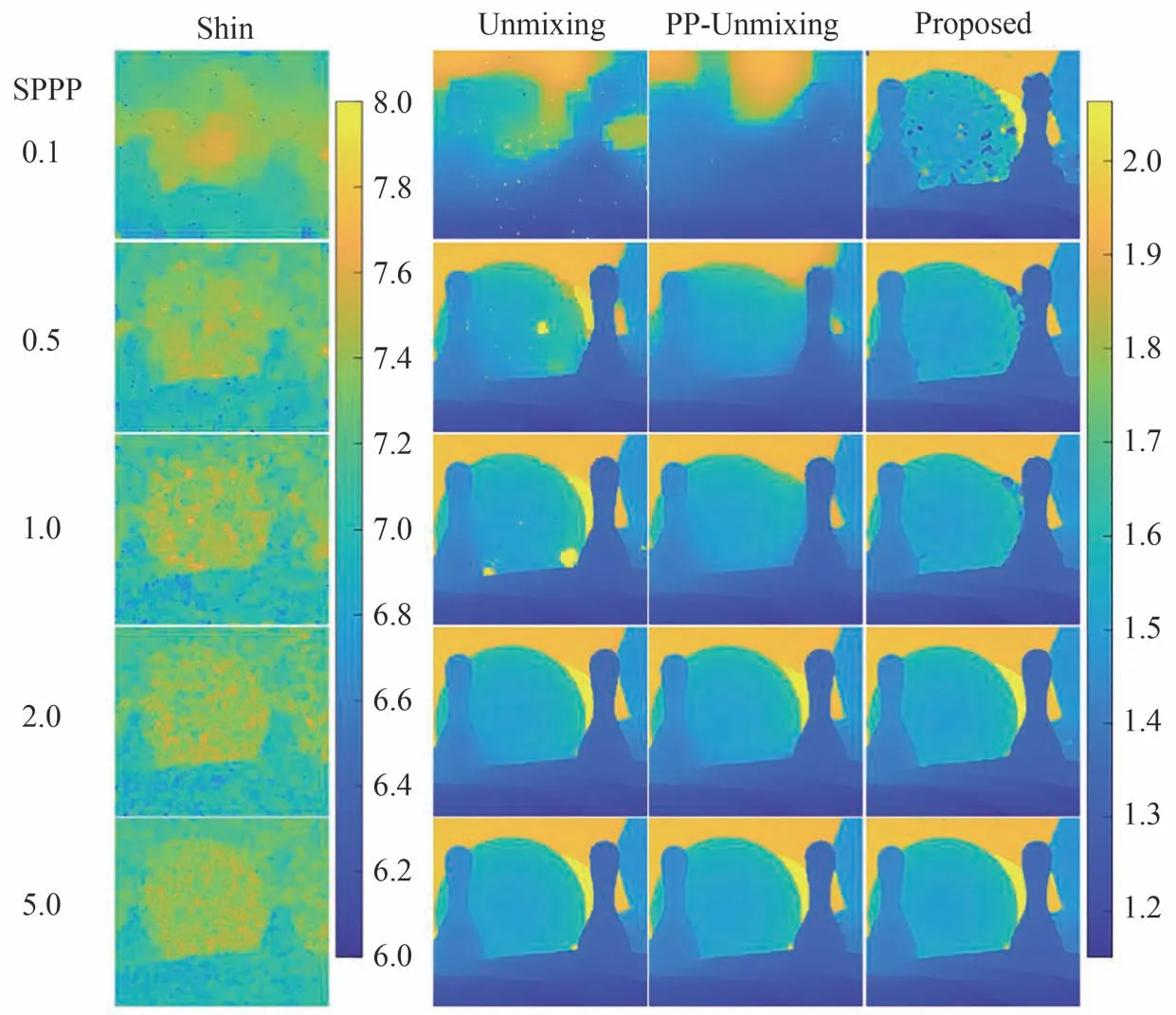
图7 信噪比为0.04 时,四种方法对于SPPP 为0.1、0.5、1、2、5 的保龄球数据的重建结果Fig. 7 When SBR=0.04, the reconstruction results of the four methods for bowling data with SPPP of 0.1, 0.5, 1, 2, and 5
由图7 和表2 可知,在信噪比为0.04 的强噪声环境中,SHIN D 提出的方法虽然运算速度很快,但对深度范围的估计具有较大偏差,因此场景一直淹没在噪声中,RMSE 也维持在米量级。Unmixing 方法对噪声的抵抗能力较强,但在SPPP 小于2 时仍会有一些残余噪点没有被消除。在SPPP 为0.1 的极端环境中,Unmixing 方法的处理结果已经不能分辨出场景信息。且该方法运算速度与SPPP 成反比,当SPPP 为5 时,耗时达到632.3 s。PP-Unmixing 方法相较于Unmixing 方法,无论在重建效果还是运算速度方面都有提升,证明了深度范围选取的必要性。但在SPPP 为0.1 时不能分辨场景信息。相比之下,本文所提方法在任何一种情况中都可分辨出场景边缘,且对噪点的处理优于其他三种方法。另外,方法平均耗时(全部数据)仅为25.1 s。该方法更适用于低信噪比和少光子环境,同时也是一种快速重建方法。
2.2 实验数据验证
除仿真验证之外还开展了实验验证。实验系统如图8(a),照明光源是波长为532 nm、脉宽为70 ps 的脉冲激光器,型号LDH-D-TA-530(德国PicoQuant 公司)。32×32 的SPAD 阵列PF32 探测器用来接收回波光子,阵列尺寸是1.6 mm×1.6 mm,探测器每个像素自带独立的时间数字转换器(Time to Digital, TDC),计时分辨率为55 ps。

图8 实验系统与目标场景Fig. 8 Experimental system and target scene
目标场景为如图8(b)所示的倾斜街景模型,从目标到探测器SPAD 阵列距离约为3.04 m,激光脉冲重复频率为20 MHz。在开灯环境下采集飞行时间数据,信噪比约为0.09。在此环境下,开展了多组数据的重建,这些数据的SPPP 在0.47~18.73 不等。实验中,仅对比SHIN D 的方法、Unmixing 方法及所提的方法。部分对比结果如图9。三种方法处理结果的RMSE 和耗时随SPPP 的变化情况如表3。

表3 信噪比为0.09 时,三种方法的重建结果随SPPP 变化的均方根误差和消耗时间Table 3 The RMSE and consumption time of the reconstruction results of the three methods vary with various SPPP at SBR=0.09
由图9 可知,SHIN D 的方法不能准确估计深度范围,导致重建深度图具有较大偏差。但由表3 可知其运算速度仍然迅速。Unmixing 方法在重建效果上优于SHIN D 的方法,但场景不够完整且对噪声处理不够彻底,在SPPP 为0.47 和0.94 时,不能分辨场景细节信息。且其运行速度很慢,最短耗时也达到81.0 s。相比之下,所提方法即使在SPPP 最小的情况下依然能够分辨场景,且能保持0.032 m 的RMSE,最长耗时也仅为37.2 s。
除了街景场景,还对另一实验目标场景进行了重建,目标场景及其深度参考真值如图10(a),包含模拟街景:房屋、花、树、墙四部分,以A、B、C、D 表示,从左至右两两间距分别为7 cm、3 cm、6 cm。目标场景距离成像系统约3 m,成像区域大小为10 cm×10 cm,所获取的飞行时间数据信噪比约为0.3,其他具体实验细节参考本课题组之前的工作[26]。

图10 目标场景、深度参考真值及三种方法对SPPP 为0.7、 2.3、 4.4、 10.7、21.6、 108.0 的飞行时间数据的重建结果Fig. 10 Target scene, depth reference ground truth and reconstruction results of time-of-flight data with SPPP of 0.7, 2.3, 4.4,10.7, 21.6 and 108.0 by three methods
同样地,实验中仅对比SHIN D 的方法、Unmixing 方法及所提方法。对比结果如图10(b)。三种方法处理结果的RMSE 和耗时随SPPP 的变化情况如表4。可以看出,相较于其他两种方法,在SPPP 大于2 时,所提方法可以将树木和花的轮廓清晰地呈现出来,且细节信息更加丰富,在SPPP 大于4 时,房子的轮廓及细节信息也逐渐完善。在SPPP 为0.7 的少光子环境下,所提方法虽然没有将场景完整地重建出来,但相较于另外两种方法在目标的完整度和重建分辨率方面仍具有明显的优势。除此之外,从RMSE 和消耗时间的结果来看,SHIN D 的方法仍然保持着最快的重建速度,但RMSE 仍是最大的,Unmixing 方法的RMSE 与所提方法不相上下,但重建速度仍是最慢的。因此,总体来看所提方法在各种光子环境下的重建效果都优于其他两种方法。
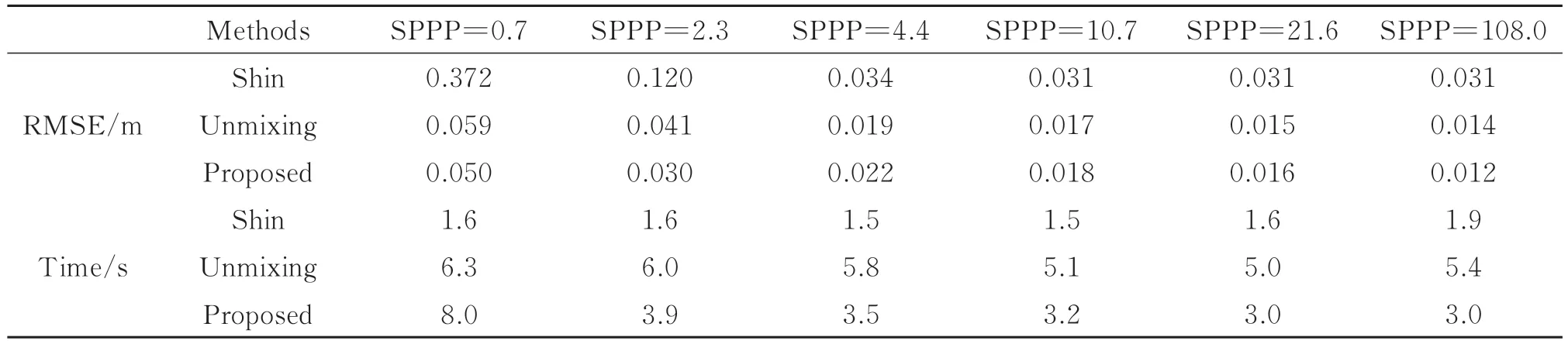
表4 三种方法的重建结果随SPPP 变化的均方根误差和消耗时间Table 4 The RMSE and consumption time of the reconstruction results of the three methods vary with various SPPP
综上,所提方法无论对仿真数据还是实验数据的重建均具有显著效果,证明该方法可用于低信噪比、各种光子水平的情况,在运算速度上也表现良好。
3 结论
本文提出并验证了基于深度范围选取的高光子效率重建算法。通过目标深度区间选取、空缺像素自适应补充与图像正则化重建两个步骤实现了对噪声的强抵抗能力,并提高了光子利用效率。其中,基于场景深度范围选取的光子筛选可以有效地去除大部分噪声,为后续处理过程提供较高质量的数据。自适应邻域补充提高了光子利用效率,解决了极少量回波光子像素空缺问题。最后,TV 正则化过程去除了残余噪声,进一步提高图像质量。通过仿真与实验数据测试,该方法可以在低信噪比、极少光子环境下进行目标精确三维重建,此外所提方法对场景内存在多个深度目标的情况有较好的适用性。

