考虑原子亚稳态的镥金属蒸发过程模拟研究
赖赣平 张晓卫
1) (清华大学工程物理系,北京 100084)
2) (粒子输运与富集技术国防科技重点实验室,天津 300180)
镥-177 是目前全球医用同位素的研究热点之一,可使用通过电子束物理气相沉积技术(EB-PVD)辅助生产和加工的镥-176 经由反应堆辐照制得.金属蒸发过程是EB-PVD 的重要一环,金属原子蒸气的各宏观特征量分布将直接影响后续的沉积镀膜过程.本文基于直接模拟蒙特卡罗方法,将原子亚稳态引入碰撞假设,建立了金属蒸发过程的二维和三维模型,对是否考虑镥原子亚稳态的金属蒸发过程中各宏观特征量进行分析比较,并对中心处宏观特征量随狭缝开口大小和蒸发源表面温度的变化特点进行讨论.研究结果表明,原子亚稳态会导致经过束流装置的金属原子蒸气数密度降低、运动速度和速度的离散程度上升,同时狭缝开口大小和蒸发源表面温度均会引发金属原子蒸气宏观特征量分布的变化.在二维模型基础上进行的三维模拟结果与其变化一致,本工作可为电子束金属蒸发过程的实验研究提供参考和指导.
1 引言
金属元素镥具有多种同位素,其中镥-177 是目前全球医用同位素的研究热点之一.镥-177 的半衰期为6.64 d,其发射的β 射线可应用于肿瘤的放射性靶向治疗,同时伴随发射的γ射线可应用于SPECT 显像[1].随着镥-177 药物的快速研发和临床研究,镥-177 的市场需求量逐年上升,掌握镥-177 的制取工艺是目前相关领域的重点研究目标[2-4].镥-177 可通过反应堆辐照镥-176 制得[5],镥-176 则可使用电子束物理气相沉积技术(electron beam physical vapor deposition,EB-PVD)进行辅助生产和加工.EB-PVD 是目前制备和加工高熔点金属和非金属材料的重要方法之一,具有蒸发温度高、镀膜纯度高、热效率高、精密易控等优点,被广泛应用于航空航天、国防军工等领域,如钢带表面镀膜、热障涂层制备等[6-9].金属蒸发过程的目的是将固态金属转变为金属原子蒸气,一般将其划分为金属在坩埚内的熔化流动和液态金属表面的蒸发膨胀两部分.金属蒸发过程是EB-PVD 的重要环节之一,金属原子蒸气的热布居分布、密度分布、速度分布、温度分布等各项物理特性分布对于之后的沉积镀膜过程具有一定的影响,同时与金属蒸气原子的利用率等相互关联[10].
目前,国内外已有众多相关学者针对金属蒸发过程进行了大量的理论和实验研究,包括坩埚内金属熔池和蒸发空间内的金属原子蒸气的各项物性研究.就金属原子蒸气而言,熔池表面温度与表面面积、熔池表面金属原子蒸气的Knudsen 数、电子枪的功率和束宽[11,12]、背景气体[13]和束流装置[14-17]等因素都会对金属原子蒸气的密度、温度、运动速度等宏观物理量产生影响.Fan 等[18]利用元素周期表外推金属蒸气输运系数,对钇蒸气使用直接模拟蒙特卡罗方法(direct simulation Monte Carlo,DSMC)进行模拟,得到与实验数据相符合的结果.在现有的理论研究中,金属原子通常被认为均处于基态,不考虑其余能级的作用.然而金属蒸发过程通常需要在较高的温度下进行,此时由于热布居分布有相当比例的原子处于更高的亚稳态上,因此研究原子亚稳态对于金属蒸发的影响是十分必要的,对镥而言更是如此.Balakrishnan 等[19]研究了电子能级对钛气相沉积的影响,模拟结果与实验结果较为相符.谢国锋等[20]曾对二维平面蒸发的亚稳态原子退激过程进行理论模拟,得到原子蒸气密度分布、速度分布、温度分布等数据,但其并未对原子的亚稳态分布进行细致分析讨论,得到的结果较为粗略.
本文基于DSMC 方法[21],引入考虑原子亚稳态的碰撞假设,建立金属蒸发过程的二维和三维模型.基于此模型,首先考察是否考虑原子亚稳态对金属蒸发过程各项宏观特征量分布的影响,然后讨论中心位置处金属蒸气各项宏观特征量针对关键参数的变化特点,最后在二维模拟结果基础上进行三维模拟,为后续针对金属蒸发过程的研究和实际生产过程起到一定的借鉴和参考作用.
2 物理模型
2.1 蒸发装置与金属蒸发过程简介
蒸发装置主要由坩埚、束流装置、蒸发区域和基底几部分组成.固态金属放置于坩埚之中,电子束轰击加热固态金属使之熔化形成液态金属熔池,熔池表面的金属原子则继续受热蒸发膨胀成为蒸气原子.金属蒸气原子进入上方蒸发区域后发生剧烈碰撞,其中一部分原子返回液态金属表面被重新吸收,另一部分原子则远离蒸发源进一步蒸发膨胀形成金属原子蒸气.金属原子蒸气通过束流装置的狭缝口形成原子蒸气束流进入蒸发区域,最终运动到基底或蒸发装置侧壁处发生冷凝并附着于其上.
2.2 碰撞假设
在金属蒸发过程中,金属原子从液态金属熔池表面进入上方蒸发区域形成金属原子蒸气.在一定的温度之下,蒸气原子将会依照Boltzmann 分布确定其热布居状态,即在各能级的分布比例.Boltzmann 分布如下式所示[22]:
其中,Ni,gi和Ei与Nj,gj和Ej分别为 处于第i激发态和第j激发态的原子数、能级简并度和能级能量,k为Boltzmann 常数,T为金属原子蒸气的温度.
镥的熔点为1936 K,沸点为3668 K.镥前5 个能级在2000–3000 K 温度下的热布居分布比例如图1 所示,各能级使用能级1–5 进行编号,其中能级3 和能级4 的热布居分布比例扩大了10 倍,能级5 的热布居分布比例扩大了1000 倍.

图1 镥前5 个能级的热布居分布比例Fig.1.Thermal population distribution proportion of lutetium’s first five energy levels.
从图1 可见,镥能级5 的热布居分布比例与前4 个能级相差2–3 个数量级,因此在实际计算模拟时只需考虑镥的前4 个能级即可.
亚稳态能级的寿命也是需要考察的因素.通常而言,原子的亚稳态能级寿命为毫秒量级.如果原子两次碰撞的平均时间间隔远短于原子的亚稳态能级寿命,则可不考虑其影响;如果两者相近,则需对此着重考虑;如果远大于能级寿命,则考虑亚稳态能级已无实际意义.结合实际工况的具体讨论见3.2 节.
两个原子的非弹性碰撞满足动量守恒和能量守恒,二维非弹性碰撞的能量变化示意图如图2 所示.在质心坐标系中,存在如下的能量守恒关系:
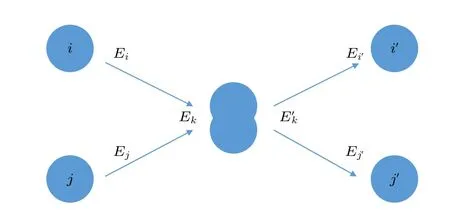
图2 二维非弹性碰撞的能量变化示意图Fig.2.Schematic diagram of the energy change in a twodimensional inelastic collision.
其中,i,j与i′,j′分别为两原子碰撞前后各自的能级,Ei,Ej与,分别为各能级的能量,Ek和分别为两原子碰撞前后相对于质心系的总动能.
碰撞后两原子所处的新能级不确定,可视作为一个概率事件.为确保两原子碰撞后相对于质心系的总动能非负,使碰撞过程具有实际物理意义,需要对碰撞后两原子所处的能级i′和j′进行限制.碰撞后两原子所处的能级i′和j′的概率P(i′,j′) 可以通过下式进行计算:
利用(3)式进行随机抽样,即可确定碰撞后两原子所处的能级i′和j′.之后再利用(2)式,即可得到两原子碰撞后相对于质心系的总动能,进而可求出两原子碰撞后的相对速度大小.最后对空间进行各向同性分布抽样,即可确定相对速度的方向.
2.3 宏观特征量的计算方法
本文主要考察的宏观特征量包括金属原子蒸气的数密度n、总运动速度的离散程度T和x,y,z方向平均速度ux,uy,uz.三者可分别反映金属原子蒸气的空间分布状态、热运动状态和平动状态.具体计算公式[23]分别为
其中,M为每个模拟分子所代表的真实蒸气原子数,N为采样得到的总模拟分子数,f为采样次数,V为空间体积,m为金属蒸气原子质量,vi=(vxi,vyi,vzi) 为第i个模拟分子的运动速度.为便于后续分析与讨论,进行归一化处理,得到
其中,nS,TS和vS分别 为蒸发源表面的模拟分子数密度、温度和模拟分子正方向平均速度.为方便叙述,后文统一将归一化符号“*”略去.
3 模拟结果
3.1 金属蒸发模型参数
二维模型可以清晰展现出各宏观特征量的空间分布情况和关键参数对金属原子蒸气的影响,得到定性的分析结果.在此基础之上搭建的三维模型可为后续电子束金属蒸发过程的实验研究提供理论支持.
二维和三维模型示意图如图3 所示.由于整个二维模型为轴对称结构,因此实际的模拟区域为右半部分,另一半区域的模拟结果通过镜像得到.蒸发装置下方为坩埚,坩埚上表面中央设置有一个长度为a的蒸发源.以蒸发源的尺寸a作为基准,整体的蒸发装置模拟蒸发区域为一个宽度和高度分别为 20a和 40a的矩形.蒸发源上方设置有一个宽度和高度均为 10a的矩形束流装置,束流装置分为侧壁和上壁两部分,并将面对蒸发源的一侧定义为内侧,另一侧定义为外侧.束流装置上方设置有一个宽度为a的狭缝.三维模型则是在二维模型的基础之上沿y轴正方向进行延展,整个模型基于x轴和y轴对称,因此实际的模拟区域为整个区域的1/4,其余区域的模拟结果通过镜像得到.此时,蒸发源为一个长度和宽度分别为a和 0.4a的矩形,狭缝为一个长度和宽度分别为 8a和a的矩形.在y轴正方向上,蒸发装置尺寸为 20a,束流装置尺寸为10a.与蒸发源表面蒸气原子的平均自由程相比,a大致相当于1000 倍的平均自由程长度.
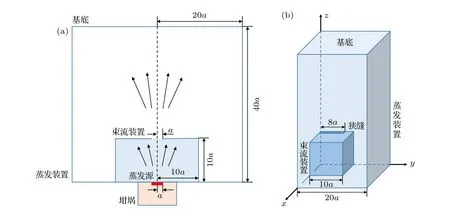
图3 二维和三维模型示意图 (a) 二维模型;(b) 三维模型Fig.3.Schematic diagram of two-dimensional and three-dimensional models: (a) Two-dimensional model;(b) three-dimensional model.
二维模拟计算分为考虑镥元素原子亚稳态和不考虑镥元素原子亚稳态两种工况.蒸发源的表面温度为TS,蒸发源表面的蒸气原子速度分布使用方向为远离蒸发源表面、温度为TS的半边Maxwell分布[24],蒸发装置和束流装置壁面温度均为 0.5TS,蒸发装置内壁和束流装置外侧壁面均为完全吸收边界,束流装置内侧壁面和底面的吸收率为0.8.本文使用的蒸气原子碰撞模型为变径硬球(variable hard sphere,VHS)模型.二维模型总网格数为20000,三维模型总网格数为2000000,时间步长为5×10-8s,模拟原子蒸气于第40000 步达到稳定并开始采样,二维模型总模拟步数为200000,三维模型总模拟步数为300000.模拟原子蒸气达到稳定时,二维模型总宏粒子数为40000–50000,三维模型总宏粒子数约为120000.
3.2 二维模拟结果
在二维模型两种工况之下,金属原子蒸气的数密度n、总运动速度的离散程度T,x方向平均速度ux和z方向平均速度uz的空间分布如图4 所示.为便于进行比较,每张图的左半部分为不考虑镥原子亚稳态的模拟结果,右半部分为考虑镥原子亚稳态的模拟结果.

图4 金属原子蒸气各宏观特征量的二维空间分布(左为不考虑原子亚稳态,右为考虑原子亚稳态) (a) 数密度 n ;(b) 总运动速度的离散程度 T ;(c) x 方向平均速度 ux ;(d) z 方向平均速度uzFig.4.Two-dimensional spatial distribution of macroscopic characteristic quantities of metal atomic vapor (left is not considering atomic metastable states,right is considering atomic metastable states): (a) Number density n ;(b) the discrete degree of total motion velocity T ;(c) average velocity ux in the x -direction;(d) average velocity uz in the z -direction.
从图4 可以观察到金属原子蒸气在蒸发装置中的运动具有明显的特征.当蒸发源达到一定温度之后,大量金属原子脱离液态金属表面形成金属原子蒸气,此处的原子蒸气具有极高的数密度.原子蒸气在蒸发源上方发生剧烈碰撞,其中一部分原子蒸气返回液态金属表面被重新吸收,另一部分则远离蒸发源并进一步膨胀,导致原子蒸气的运动速度增大,同时原子蒸气的数密度减小.此时原子蒸气的平动动能主要由内能转化而来,因此原子蒸气的速度离散程度也逐渐下降.由于束流装置阻挡,狭缝附近的束流装置内侧有较多的蒸气原子囤积,导致原子蒸气数密度升高.原子蒸气被束流装置阻挡之后,一部分原子蒸气被束流装置吸收,其余原子蒸气则被反射回束流装置腔内.这部分被反射的原子蒸气与其他原子蒸气发生碰撞,使得原子蒸气的运动速度发生剧烈变化,导致原子蒸气的速度离散程度明显升高.束流装置的侧壁和上壁分别对原子蒸气x和z方向平均速度产生了较大的约束作用.当金属原子蒸气通过狭缝之后,金属原子蒸气的宏观特征量如速度、数密度、速度的离散程度等变化逐渐减小,形成稳定的金属原子蒸气束流,并最终运动到基底或蒸发装置内壁发生冷凝附着于其表面.
可以看出,在考虑原子亚稳态之后,蒸发源处竖直方向上数密度的值明显降低;原子蒸气在中心束流处速度的离散程度明显升高,同时其在竖直方向上的变化幅度明显大于水平方向;原子蒸气x和z方向平均速度均有一定程度的提升,后者的提升更为显著.出现该现象的原因是,原先处于高能级的蒸气原子经过大量的碰撞,能级能量逐渐转换为原子蒸气的平动动能和热运动动能,这体现为原子蒸气平动速度的提升和热运动的加剧.是否考虑亚稳态并不会影响从蒸发源处进入的蒸气原子数目,而考虑原子亚稳态之后更高的z方向平均速度导致原子蒸气在竖直方向上的数密度减小.束流装置内侧附近的速度离散程度在考虑能级亚稳态之后出现了一定程度的降低,这是因为有部分原子蒸气的平动动能转化为蒸气原子的能级能量而不是原子蒸气的热运动动能.
在蒸发源表面温度为TS时,镥考虑原子亚稳态的能级占比分布图如图5 所示.从图5 可以看出,在蒸发区域内,绝大部分蒸气原子处于能级1即基态,各亚稳态主要出现于蒸发源表面和束流装置上壁及侧壁内侧,尤其在束流装置拐角处具有较高的占比.这是因为,蒸发源表面的高能态原子主要来源于出射原子热布居分布比例符合Boltzmann分布的蒸发源,随着碰撞的发生高激发态的蒸气原子逐渐退回基态,蒸气原子的亚稳态能级能量转化为原子蒸气的平动动能和热运动动能;束流装置内侧的高能态原子则来源于被束流装置阻挡反射的原子蒸气,这部分原子蒸气与未反射原子蒸气相比具有较大的相对运动速度,导致碰撞之后蒸气原子具有足够的能量激发到高能态,此时能量由原子蒸气的动能重新转化为蒸气原子的亚稳态能级能量.

图5 各能级占比分布图 (a) 能级1;(b) 能级2;(c) 能级3;(d) 能级4Fig.5.Layout of the proportion of each energy level: (a) Energy level 1;(b) energy level 2;(c) energy level 3;(d) energy level 4.
根据(2)式可知,蒸气原子的能级能量和原子蒸气的相对运动动能可以随着碰撞发生转移,在碰撞越剧烈的区域能量转移得越充分.在经过大量的碰撞以及束流装置的整流之后,原子蒸气转变为各物理参数相近的金属原子蒸气束流.由于原子蒸气之间的相对速度减小,相对运动动能将不足以支撑蒸气原子跃迁到高能级,使得越来越多的蒸气原子处于基态能级.
束流装置上壁外侧区域的蒸气原子则主要来源于被束流装置阻挡反射的原子蒸气,其有相当比例处于亚稳态能级上,这部分蒸气原子被中心的蒸气束流带动从而沿着狭缝口边缘逸出.之后中心原子蒸气束流在狭缝开口处发生剧烈碰撞.这部分蒸气原子中向束流方向运动的参与到碰撞之中逐渐回归基态;向侧向运动的蒸气原子则由于侧向位置的数密度较低,发生碰撞较少,得以能够保持住亚稳态能级继续向侧向运动,这在图5 中表现为处于亚稳态能级的蒸气原子向侧向运动.
最后,在此对亚稳态能级寿命对模拟结果的影响进行评估.本文所讨论的工况在不同位置处的平均自由程有较大差异.在蒸发源表面,蒸气原子的平均自由程约为10-5m,在狭缝开口上方约为10-3m,原子蒸气的运动速度数量级约为102m/s,因此蒸气原子两次碰撞的平均时间间隔为10-4–10-2ms,这一般短于亚稳态能级寿命.因此,在束流装置内部以及中心蒸气束流处可不考虑亚稳态能级寿命对蒸气原子碰撞的影响.而在侧面数密度较低的区域,可能会出现蒸气原子运动时间间隔超出亚稳态能级寿命的情况,但此区域对本文的重点研究内容关系较低,因此本模拟可不考虑亚稳态能级寿命的影响.
3.3 狭缝开口大小对原子蒸气宏观特征量的影响
根据金属真空蒸发的特点可知,在蒸发源中心位置处沿着垂直于蒸发源表面方向上的宏观特征量变化最为显著.为讨论狭缝开口大小对原子蒸气宏观特征量的影响,取蒸发源表面温度为TS,设置狭缝开口大小分别为a,1.5a和 2a,以及是否考虑原子亚稳态共6 种工况.中心处的金属原子蒸气在6 种工况之下的数密度n、总运动速度的离散程度T和z方向平均速度uz如图6 所示.图中虚线为狭缝所在位置.

图6 金属原子蒸气在蒸发源中心位置处的宏观特征量变化曲线(不同狭缝开口大小) (a) 数密度 n ;(b) 总运动速度的离散程度 T ;(c) z 方向平均速度uzFig.6.Variation curves of macroscopic characteristic quantities of metal atomic vapor at the center of the evaporation source (different slit opening sizes): (a) Number density n ;(b) the discrete degree of total motion velocity T;(c) average velocity uz in the z -direction.
从图6 可以看出,各宏观特征量受到原子亚稳态影响的变化特点与前文的结果一致,即数密度降低、总运动速度的离散程度和z方向平均速度升高.在束流装置内部,仅狭缝开口大小不同的金属原子蒸气的各项宏观特征量基本一致;而在通过狭缝之后,这几个宏观特征量出现了反常的突起现象,突起随着狭缝开口的收窄而逐渐向狭缝位置靠近并越发明显,并且在考虑原子亚稳态之后突起程度有所降低;当狭缝开口大于 2a后,反常突起基本消失.这是因为当狭缝开口较小时,将有大量的原子蒸气受到阻挡反射而沿着狭缝边沿飞出,这些原子蒸气的运动方向偏向于中心位置收束,导致在通过狭缝之后原子蒸气的数密度上升.同时随着狭缝开口的收窄,这些原子蒸气的运动方向偏转也逐渐增大,导致突起部位越发靠近狭缝位置.随着金属原子蒸气的数密度增大,原子蒸气之间的碰撞更加频繁,使得原子蒸气的运动更加无序,这体现在突起部位原子蒸气的总运动速度的离散程度的上升和z方向平均速度的下降[25].而在考虑原子亚稳态之后,在突起部位部分发生碰撞的原子蒸气的动能转化为蒸气原子的亚稳态能级能量,因此突起程度均有所削减.
3.4 蒸发源表面温度对原子蒸气宏观特征量的影响
为讨论蒸发源表面温度对原子蒸气宏观特征量的影响,取狭缝开口大小为a,设置蒸发源表面温度分别为TS,1.125TS和 1.25TS,以及是否考 虑原子亚稳态共6 种工况.中心处的金属原子蒸气在6 种工况之下的数密度n、总运动速度的离散程度T和z方向平均速度uz如图7 所示.图中虚线为狭缝所在位置.

图7 金属原子蒸气在蒸发源中心位置处的宏观特征量变化曲线(不同蒸发源表面温度) (a) 数密度 n ;(b) 总运动速度的离散程度 T ;(c) z 方向平均速度uzFig.7.Variation curves of macroscopic characteristic quantities of metal atomic vapor at the center of the evaporation source (different surface temperatures of evaporation source): (a) Number density n ;(b) the discrete degree of total motion velocity T ;(c) average velocity uz in the z -direction.
从图7 可以看出,随着蒸发源表面温度的上升,金属原子蒸气的数密度下降速度减缓,总运动速度的离散程度升高,z方向平均速度降低,同时在通过狭缝之后反常突起逐渐减弱.出现该现象的原因是,蒸发源表面温度的上升意味着蒸发速率的增大和蒸气原子在亚稳态能级上布居分布比例的提升.蒸发源温度升高后,相同时间有更多的蒸气原子从蒸发源表面进入蒸发源上方中心位置处,同时伴随有更多被束流装置阻挡反射后的原子蒸气回到中心位置,因此在此区域原子蒸气的数密度能够比温度升高之前下降速度减缓;同时由于反射的原子蒸气与其余原子蒸气的混合碰撞更为剧烈,导致原子蒸气总运动速度的离散程度升高以及z方向平均速度降低.狭缝开口处的异常突起是由于原子蒸气束流受到狭缝约束被迫收窄,导致在狭缝开口处蒸气束流的数密度上升、碰撞加剧进而导致局部出现z方向平均速度下降以及总运动速度的离散程度上升.当蒸发源温度升高后,在蒸发源上方原子蒸气碰撞加剧,原子蒸气的数密度分布更为集中,分析数密度分布数据可以发现在狭缝开口处大部分原子蒸气更加贴近中心位置,被阻挡改变运动方向的原子蒸气比例降低,狭缝约束作用减弱,蒸气束流得以维持原有状态,这即体现为异常突起逐渐消解.
3.5 三维模型结果
在三维模型工况之下,金属原子蒸气的数密度n、总运动速度的离散程度T和x,y,z方向平均速度ux,uy,uz的空间分布如图8 所示.

图8 金属原子蒸气各宏观特征量的三维空间分布 (a) 数密度 n ;(b) 总运动速度的离散程度 T ;(c) x 方向平均速度 ux ;(d)y方向平均速度 uy ;(e) z 方向平均速度uzFig.8.Three-dimensional spatial distribution of macroscopic characteristic quantities of metal atomic vapor: (a) Number density n ;(b) the discrete degree of total motion velocity T ;(c) average velocity ux in the x -direction;(d) average velocity uy in the y -direction;(e) average velocity uz in the z -direction.
从图8 可以看出,由于三维模型狭缝开口为长度为 8a,宽度为a的矩形,因此在x方向和y方向上各宏观特征量的空间分布特点具有显著差异,在x方向上各宏观特征量主要集中于中心束流,而在y方向上则更加逸散.这是因为,在x方向上,窄狭缝口使得原子蒸气束流更为收紧,大部分蒸气原子在束流内以相近的运动状态向上方运动,导致各宏观特征量空间分布相对集中.狭缝x方向开口与二维模拟尺寸相当,因此在这个方向上各宏观特征量的分布特征与之前的模拟结果相近.而在y方向上,极宽的狭缝开口几乎已经无法对向上运动的原子蒸气产生明显影响,具有侧向速度的原子蒸气可以较少受到狭缝约束而继续侧向运动,这与直接不添加束流装置的空间分布十分接近.在3.3 节中已经讨论过狭缝开口大小对宏观特征量的影响,当狭缝开口大于 2a后,反常突起现象近乎消失,束流装置约束作用将大打折扣.
与二维模拟的结果相比,三维模拟结果的数据分布数量级和空间分布形态均呈现出一致的变化规律.三维模型可为金属原子蒸发的后续研究和实际实验和生产过程提供参考和指导.
4 结论
本文基于DSMC 方法,就金属镥蒸发过程中各宏观特征量受到原子亚稳态的影响进行数值模拟.本文将原子亚稳态纳入原子碰撞假设之中,构建了镥原子蒸气蒸发过程的二维和三维模型,计算模拟了考虑原子亚稳态条件下的金属蒸发过程,得出结论如下: 考虑原子亚稳态之后,在束流装置上方金属原子蒸气的数密度降低、运动速度和速度的离散程度上升,同时金属原子蒸气宏观特征量分布与狭缝开口大小和蒸发源表面温度均有关联.在此基础之上建立的三维模拟的结果与二维模型呈现出一致的变化规律,为电子束金属蒸发过程的实验研究提供了一定的参考和指导.

