利用整帧翻转的SRAM型FPGA故障注入加速算法*

孙鹏跃,吕晟莱,毛二坤,张书政,陈 雷,周 欢,黄仰博,楼生强

(国防科技大学 电子科学学院, 湖南 长沙 410073)

静态随机存取存储器(static random access memory,SRAM)型现场可编程门阵列(field programmable gate array,FPGA)凭借其高性能、低成本、低功耗、可重配置等优点,以及随着其集成度的不断提高,逐渐开始应用于航空航天领域[1-3]。但是由于SRAM型FPGA的结构特点,以及空间中强辐射环境的作用,SRAM型FPGA容易受到外太空中的高能粒子作用而发生单粒子效应,其主要表现为单粒子翻转(single event upset, SEU)[4-6]。2007年至2010年我国航天器单粒子效应故障的统计表明,单粒子效应在空间环境辐射效应中占据主导地位,对航天器的危害日益严重。

当前针对SRAM型FPGA中单粒子效应的评估方法主要由四种:一是利用航天器搭载FPGA进行高辐射试验,该方法虽然准确性高,但是成本高,周期长[7-8];二是利用高能粒子辐射,该方法虽是目前业界公认的权威方法,但其不能实现准确注入,试验机时十分紧张,且对器件存在一定的损伤[9-10];三是使用特定工具生成脉冲激光进行单粒子效应模拟,但其成本较高,且试验技术复杂[11-12];四是基于故障注入的单粒子效应模拟方法,其成本低、周期短、可控性高、复杂性低[13-15],能够实现卫星载荷抗辐照加固设计的快速迭代和优化。

目前故障注入方法主要是通过人为改变FPGA配置存储器内容的方式来实现故障注入。传统逐位翻转故障注入方法的优点是能精准全面定位敏感位(sensitive bit, SB),找到可恢复异常比特位(recoverable-SB,R-SB)和不可恢复异常比特位(unrecoverable-SB,UR-SB)[16-17]。但由于SRAM型FPGA配置数据比特位数量庞大,逐位翻转耗时太长,效率低,无法在设计前期快速迭代。大量逐位翻转试验结果表明,造成整个设计功能异常的大多是R-SB,这类异常可通过刷新修复,不会造成持续性的功能异常;只有少量的异常比特位会造成持续性的功能异常,必须通过在轨重加载恢复,这类异常的影响极大,会造成在轨服务的长时间中断。工程中更加关注会造成持续异常的情况,即UR-SB,但由于UR-SB占比很少,若采用传统逐位翻转的测试方法,耗时太长,不利于抗辐照设计优化快速迭代,因此,必须设计一种快速发现UR-SB的加速故障测试方法。

为了解决UR-SB的快速定位问题,本文提出一种基于整帧翻转的SRAM型FPGA的故障注入加速试验方法,该方法不再采用传统逐位翻转的思路,而是对配置文件进行整帧注错,刷新修复后验证整个设计的功能异常,以快速模拟故障注入,缩短试验耗时,快速定位UR-SB精确位置。

1 传统逐位翻转故障注入算法

建立故障注入试验模型,其中包含被测单元(unit under test, UUT)、参考单元(reference unit, RU)、刷新单元(scrub unit, SU)以及控制单元(control unit,CU)组成。其中:UUT运行待测试配置项,并接受控制单元的故障注入;RU运行与被测单元功能相同的配置项,作为功能参考标准;SU通过动态局部刷新实现对UUT的故障注入,并完成对UUT和RU等的全局加载;CU完成对UUT和RU的配置,并负责结果比对、记录和整个故障注入过程的控制。整个模型设计如图1所示。

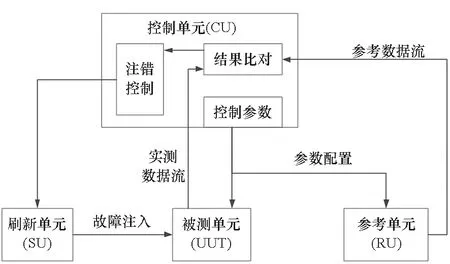
图1 故障注入试验模型Fig.1 Test model of fault injection

传统逐位翻转故障注入算法流程简述如下:

Step1:配置初始化。完成对整个故障注入平台的加载和功能配置。

Step2:UUT逐位翻转。当未达到最大比特数时,SU逐比特对UUT配置数据进行取反,实现故障注入,否则执行Step 5。

Step3:结果判定。CU对UUT和RU的数据流进行比对并记录,若正确,则返回Step 2,否则执行Step 4。

Step4:刷新后再验证。SU修复当前注入的错误比特,再次判定比对结果并记录,若正确,则返回Step 2,否则,记录当前注错位置,返回Step 1。

Step5:统计结果,完成测试。

从上面的逐位翻转故障注入测试过程可知,其能全面、精准定位所有敏感位,发现R-SB和UR-SB。但FPGA配置数据比特位数量庞大,逐位翻转耗时太长。卫星载荷在轨运行情况表明,UR-SB无法通过定时刷新修复,必须通过在轨重新加载恢复,会造成在轨服务的长时间中断。而大量故障注入结果表明,UR-SB仅占整个SB中的极少部分,若采用传统逐位翻转的测试方法,效率极低。

2 基于整帧翻转的UR-SB快速定位算法

基于整帧翻转和二分法的UR-SB快速定位算法的整体思路为:首先对UUT配置数据进行整帧翻转;然后通过SU修复之前的整帧翻转操作;最后由CU比对数据流,若正确,则直接跳转到下一帧,否则,通过二分法对当前帧进行UR-SB定位。具体算法流程如图2所示。

图2 基于整帧翻转的故障注入加速算法流程Fig.2 Algorithm flow of fault injection based on the whole frame upset

基于整帧翻转的故障注入加速算法步骤如下:

Step1:配置初始化。

Step2:UUT整帧翻转。当未达到最后1帧时,SU依次对UUT进行整帧翻转,实现整帧故障注入。

Step3:刷新后验证。SU修复当前帧的整帧翻转,由CU对UUT和RU的数据流进行比对;若正确,则说明当前帧不存在UR-SB,返回Step 2,否则执行Step 4。

Step4:二分法精确定位UR-SB。执行配置初始化,采用二分法重新对当前帧进行故障注入。当第m次采用二分法时,对每段1/2m帧的所有配置数据进行翻转,返回Step 3比对结果,若正确,则说明该段1/2m帧不存在UR-SB,否则,说明该段存在UR-SB。如此反复,当二分后每段范围足够小时,直接采用传统逐位翻转故障注入,即可精确定位UR-SB位置。当前帧测试完成后记录结果,并返回Step 1,继续下一帧测试。

Step5:统计结果,完成测试。

可以看到,上述算法流程在整帧翻转后并没有马上比对UUT和RU结果,故无法发现R-SB,且整帧翻转大概率会造成UUT功能异常。相比于传统逐位翻转的故障注入方法,本文提出的基于整帧翻转的故障注入快速算法的有效性分析如下:

假设SRAM型FPGA配置文件总比特数为M,UR-SB总数为N,配置文件总帧数为L,每一帧有K比特,异常帧采用m次二分法。由于不同卫星载荷FPGA设计差异明显,难以分析SB在整个配置文件中的具体分析,故本文设定相对最优和较差的两种情况,以测试流程中的比对次数为指标,分别分析整帧翻转算法的有效性。

假设最优情况下,所有UR-SB均位于同一帧的同一段内,则这种情况下的测试次数为:

(1)

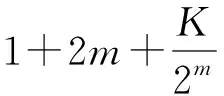
对于假定的一种较差情况,假设配置文件中每一帧都恰好包含有1 bit UR-SB,则测试次数为:

(2)

式中,N为配置文件总帧数。

对于传统逐位翻转测试方法而言,其总测试次数为M,则本文方法的测试效率相比传统方法的提升倍数P可计算为:

(3)

以目前在轨载荷应用最为广泛的XQR2V3000器件为例,其配置文件总比特数为9 582 848,总帧数为1 804,每帧有5 312 bit,假设每帧采用5次二分法。上文分析的最优情况的测试次数为1 980,较差情况的测试次数为319 308。因此,相比传统逐位翻转测试方法,本文所提算法在XQR2V3000平台上的测试效率提升倍数P为:

30≤P≤4 839.8

(4)

可以看到,本文算法的测试效率提升明显,尽管假设的较差情况和最优情况在工程实际中出现的概率均不大,但即使在较差情况下,也提升了30倍,这充分证明了本文算法的有效性。

3 试验验证

前面对本文算法在假定条件下的性能进行了理论分析,但毫无疑问,二分法次数m、配置文件总比特数M等参数必然会对算法的性能产生影响。因此,本节首先对不同参数在假定较差条件下的性能进行仿真分析,以确定在实际测试环境下的最优参数选择;在此基础上,针对本单位在轨运行的信号生成载荷的故障注入测试结果进行分析,以实测结果进一步验证算法的有效性。

针对卫星载荷在轨常用的Xilinx公司XQR2V1000、XQR2V3000、XQR2V6000型,以及目前国产化的XQR4VSX55和JFM7K325T型共5种FPGA,分析不同二分法次数m对式(3)所示的较差情况下加速测试相比于传统逐位翻转测试提升倍速的影响,如图3所示。

图3 不同FPGA注错测试加速效率Fig.3 Accelerated efficiency of different FPGAs in fault injection results

可以看到,5型FPGA的加速效率均有显著提升,特别是随着二分法次数的增加,测试效率提升倍数也越来越高。尽管这主要是由于本文假定每一帧仅有1 bit错误,但实测情况下,UR-SB本来就相对极少,且二分次数不可能太高,针对分析的5款器件,最大二分次数仅为11,即使因为二分操作会增加一部分试验次数,但这相比于百万甚至千万量级的总比特数,可忽略不计。故在实际工程中,建议选取最大的二分法次数。目前在轨载荷最常用的XQR2V3000型FPGA最大提升倍数为207,这意味着对于动辄需要几个月的逐位翻转试验,若采用本文所述的基于整帧翻转的加速注错方法,可在几天之内完成所有UR-SB的精确定位,这在卫星载荷研制初期,对于载荷配置项的抗辐照加固设计评估和提升具有重要意义。

结合针对在轨信号生成载荷的故障注入试验测试结果,进一步分析本方法在实际工程中的有效性。该载荷采用XQR2V3000器件,故障注入试验平台设计如图4所示,主要包含:被测FPGA、参考FPGA、测试FPGA、刷新控制器以及上位机组成。其中被测FPGA由1片SRAM型FPGA实现,运行被测试设计的三模加固配置项,提供实际运行场景;参考FPGA由1片SRAM型FPGA实现,运行被测试设计的单模配置项,作为功能参考标准;测试FPGA由1片SRAM型FPGA实现,负责比对被测FPGA和参考FPGA的数据流是否一致;刷新控制器由1片SRAM型FPGA实现,负责通过SelectMAP接口对被测FPGA、参考FPGA、测试FPGA进行全局加载,并实现对被测FPGA的动态局部刷新;上位机(处理器)由1片数字信号处理(digital signal process, DSP)芯片实现,与FPGA通过总线交互,所有的寄存器均可通过DSP处理器访问,控制被测FPGA、参考FPGA输出数据流,获取数据流比对结果,控制整个故障注入试验过程。

图4 XQR2V3000 FPGA故障注入试验平台Fig.4 Fault injection test system based on XQR2V3000 FPGA

在上述试验平台上对信号生成载荷逐位翻转测试方法的测试结果如下:共测试1 420帧(BRAM的对应384帧一般不进行故障注入测试),共7 543 040 bit,最终定位292个UR-SB。分析UR-SB分布情况发现,大部分帧不存在UR-SB,部分帧存在1 bit UR-SB,少数帧中存在多个UR-SB。采用本文所述的整帧翻转加速方法后,5次二分法和10次二分法的总试验次数分别为46 522和7 948,总试验次数相比传统逐位翻转测试方法的7 543 040次显著下降,不同方法的测试结果对比如表1所示。

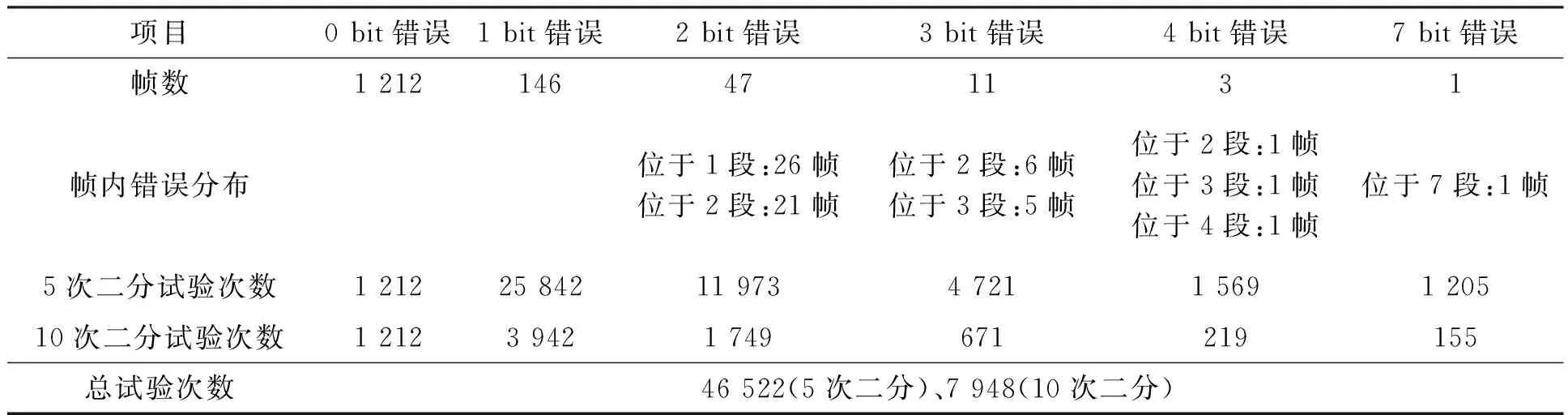
表1 实测结果分析Tab.1 Analysis of the experiment results

实测结果表明:85.3%(1 212帧)的整帧不存在UR-SB,这表明采用本文整帧翻转加速算法必然能大幅提升测试效率。当采用5次二分法时,测试次数共为46 522,是传统逐位翻转测试法的1/162,即约加速了162倍,而当采用10次二分法时,该加速倍数增加949倍,上述结果充分证明了本文基于整帧翻转测试方法的有效性。

4 结论

卫星载荷在轨发生不可恢复的SEU是目前影响在轨服务连续性的最大因素,尽管传统逐位翻转能够更加全面地定位在轨设计的敏感位分布情况,但其测试效率太低,特别是针对UR-SB的定位。本文提出了基于整帧翻转的加速故障注入算法,并采用二分法对存在UR-SB的配置帧进行快速搜索,仿真和实测结果表明,该方法能够显著提升故障测试效率。然而,整帧翻转算法无法定位R-SB,评估结果不够全面,需要根据工程应用的实际需求,与传统故障注入算法结合运用,以支撑卫星载荷在轨抗空间辐照可靠性设计。