CFO条件下的OFDM子载波调制样式识别方法*

朱立为,王 翔,王 垚,王丰华,黄知涛,2

(1.国防科技大学 电子科学学院, 湖南 长沙 410073; 2. 国防科技大学 电子对抗学院, 安徽 合肥 230037)

正交频分复用(orthogonal frequency division multiplexing, OFDM)信号作为一种多载波传输方案,以其高效率的频带利用率和频率可选择性的优点,被广泛应用于军、民用领域。技术便利也给电磁频谱空间的合理合法利用带来不少的挑战。如近些年来,在民用安全防护领域,为了对无人机非法使用的管控,催生了以无人机测控数传信号为目标的非合作接收技术研究,包括信号的检测识别、参数估计、解调及测角定位等技术问题。为了更好地完成频谱管理以及相关非法取证工作,非合作接收系统须完成对OFDM信号各子载波的解调任务。然而完成解调的前提条件是要已知子载波的调制样式,因此研究OFDM子载波的调制样式具有重要意义。

针对通信信号调制样式的识别已经有大量学者进行过研究。如文献[1-2]中,采用深度学习的方法来识别OFDM信号子载波调制,但深度学习方法比较依赖训练数据的质量,且对信号环境的范化能力也有待提高。文献[3]中采用高阶累积量的调制识别方法,用两个四阶累积量的C40和C42的比值作为特征参数F来识别单载波信号的调制样式。但对多载波OFDM信号,特征参数F并不满足其分布规律,因而无法适用。文献[4]也提出四阶累积量和六阶累积量之间的比值参数特征F来分类识别OFDM子载波调制样式,仿真发现,当存在载波偏差时,特征F的分布规律变化较大,因而失效。文献[5]将信号的多次方谱与深度学习相结合的方法来识别数字调制信号的调制样式,该方法用信号多次方谱作为训练和识别的输入,但四阶相移键控(quadrature phase shift keying, QPSK)与16阶正交幅度调制(16th order quadrature amplitude modulation, 16QAM)的多次方谱特征十分的接近,易导致错误识别,因此不太适用于OFDM信号子载波调制样式的识别。而文献[6]基于解调星座图的方法,识别时需要估计信号星座图,在未知信号调制样式的情况下去获得星座图,往往十分困难。

本文采用OFDM正交解调抽取后的基带波形的幅度分布特征和多次方谱线特征,结合统计差分的方法完成子载波调制样式的识别。该方法只采用基带波形的幅度分布特征,并不需要解调星座图,因此也不需要精确的载波同步,同样本方法也可以适应用单载波信号。本文针对OFMD子载波两簇常用调制样式展开分析识别,即相移键控(phase shift keying, PSK)系列二阶相移键控(binary phase shift keying, BPSK)、四阶相移键控、八阶相移键控(8th order phase shift Keying, 8PSK)调制,及正交幅度调制(quadrature amplitude modulation, QAM)系列的8阶正交幅度调制(8th order quadrature amplitude modulation, 8QAM)、16QAM。

1 信号模型

OFDM作为另一种多载波传输方案,与一般多载波传输(frequency multiple transmission, FMT)方案最大不同就是正交子载波频谱相互重叠带的带宽效率的提升,而子载波的正交性是由正反傅里叶变换来实现的[7-8]。

原始信息的符号流经串/并转换后,生成N个并行符号流,被不同的子载波调制后,利用反傅里叶变换实现OFDM传输,变换到指定的信号射频,经过发射机发送出去。令Xl(k)表示在第k个子载波上的第l个OFDM发送符号,l=0,1,2,…,L-1;k=0,1,2,…,N-1。由于串/并转换,N个符号的传输时间扩展为NTs,Ts表示符号X(k)的周期,它是单个OFDM符号的持续时间Tsym,即Tsym=NTs。令ψl,k(t)表示在第k个子载波上的第l个OFDM信号[9-10]。

(1)

得到基带时间连续的OFDM信号表达式:

(2)

对式(2)OFDM基带信号进行采样,令t=lTsym+nTs,Ts=Tsym/N,fk=k/Tsym,可以得到OFDM符号的离散时间表达式:

(3)

易得基带OFDM接收符号表达式为:

(4)

考虑信道的带限情况,则有Xl(k)=al,kga(t-lTs)其中,ga(t-lTs)为信号脉冲形状[10]。

因此,在加性高斯白噪声条件下的,多载波OFDM信号接收模型表达式为:

r(t)=s(t)+n(t)

(5)

OFDM信号的接收过程如图1所示。

图1 OFDM接收框图Fig.1 OFDM receiving block diagram

2 OFDM子载波基带幅相特征

由上一节的OFDM信号基带接收模型分析可知,对于OFDM子载波调制识别的输入为并/串转换后的基带信号。而由于PSK和QAM原理可知[11-12],PSK基带调制的幅度基本恒定在某一个值,其调制信息主要体现在相位的变化上;而对于QAM基带,其调制信息不但体现在相位变化上,也体现在幅度变化上。所以下面对OFDM信号子载波幅相特征进行详细分析。

2.1 子载波幅度特征分析

本文假设所有OFDM子载波已经过反傅里叶变换正交解调和并/串转换,同时也不关注信道均衡等。

并/串转换后OFDM信号所有子载波基带为:

R(k)=X(k)+W(k)

(6)

式中:n=0,1,2,…,N-1,其中N为逆离散傅里叶变换(inverse discrete Fourier transform,IDFT)点数,也等于OFDM基带子载波个数;al,k为第k个子载波的第l个符号的基带波形;ga为码元成形函数;a为基带码元幅度。同时,fd为残留载波,W(k)为高斯白噪声[13]。如果考虑定时同步时信号时延引起的相位偏差φ,则式(6)可以改为式(7)[14]。

(7)

假设OFDM的子载波调制为PSK或QAM类调制,则sl(k)中任意数据子载波s(k)可定义为[15]:

(8)

其中:n′取值在[0,nm-1]之间,跟传输的信息有关,n′=0,…,nm-1(m=0,…,M-1),M为基带信号幅度值的个数,nm为具有相同幅度值Am(复信号的模,或者说复平面上信号点到原点的距离)的符号个数;各个符号的相位不同θm,同时存在由载波残留引起的相差θd和定时同步时信号时延相位偏差φ。

子载波调制样式为16QAM时,M=3,n0=4,n1=8,n2=4,理论上具有三个标称幅度值R0,R1,R2,具有以下关系:

(9)

其他QAM调制方式以此类推。而PSK类的调制,由于只调相,所以其基带幅度只有一个值R。

2.2 子载波基带信号多次方谱分析

前面已经推导了OFDM子载波的幅度特征,下面简要分析其相位特征。

先假设只传输单用户信息的情况,即一路原始信息串并转换之后,经多路子载波传输的方式。

由上一节OFDM基带模型分析可知,其子载波基带相位可以表示为式(10)的形式[16]。

(10)

式中:m=0,1,…,M-1;θd、φ为相位偏差,对于OFDM信号一帧时间内,fd、φ可以近似固定。因此子载波基带信号的多次谱可以表示为式(11)的形式[17-18]。

当x=M时,则有:

(12)

因此,对于多阶相移键控(multi phase shift keying, MPSK)调制的OFDM子载波基带信号,在其阶数M次方谱上会出现冲激谱线。对于多阶正交幅度调制(multi quadrature amplitude modulation, MQAM)调制子载波基带信号的谱线特征,其推导过程类似,但几次方谱中出现的冲激谱线与MPSK有区别,后续仿真会验证。

3 调制样式识别的前提条件与识别策略

通过总结上一节对OFDM子载波基带信号幅度和多次方特征分析,初步确定了识别算法的方案,即用幅度分布实现调制大类的区别,结合多次谱实现调制阶数的识别。首先对本算法的前提条件做相关必要说明。

1)假设已经完成了OFDM的帧同步和定时,获取到了OFDM单个帧基带信号。

2)单个OFDM帧时间范围内,接收机载波频率偏差(carrier frequency offset, CFO)为均匀分布。

OFDM子载波调制样式识别策略的流程如图2所示。

图2 OFDM子载波调制样式识别流程图Fig.2 Flow chart of OFDM subcarrier modulation pattern recognition

1)以OFDM子载波基带信号作为识别算法的输入,对信号幅度进行直方图统计。

2)对信号幅度统计结果进行卡尔曼滤波,去除部分噪声引起的偏离;对幅度统计结果曲线进行插值,然后进行差分求导,检测其差分曲线变化来判别其幅度值的数量。

3)根据幅度数量进行PSK和QAM两大类调制的识别。

4)在PSK调制类内部,利用多次方谱特征实现调制阶数的识别。

5)在QAM调制类内部,综合利用幅度统计分布情况与多次方谱特征实现调制阶数的识别。

因此,本文通过统计基带信号的幅度分布特征和多次方谱线特征来识别OFDM子载波调制。

4 仿真分析

为了验证本文识别策略的可行性及算法时间复杂度,仿真分析设置了四个仿真实验:实验1用来验证频率偏差条件下OFDM子载波基带信号幅度分布特征和多次方谱特征是否可以作为调制识别的依据;实验2用来验证本文算法的调制识别正确率;仿真实验3为频率偏差适应能力对比分析;仿真实验4为时间复杂度对比分析。

4.1 仿真实验1:OFDM子载波幅度与谱特征分析

设接收机采样率fs=10 MHz,接收机中频频率Fc=0 MHz,符号速率Rb=1 000 kHz,信号采样点数L=1 048 576,加入的高斯白噪声信噪比变化范围为0～20 dB;子载波数为64,数据载波数为48,码片时长为0.5 μs,子载波脉冲成形g(t)采用平方根升余弦,滚降系数α=0.5,子载波调制样式分别为BPSK、QPSK、8PSK、8QAM、16QAM,产生多载波OFDM中频采样信号。

在信号接收端,正交解调后的OFDM子载波基带信号中加入归一化频偏fd/fs=0.01,子载波基带信号的幅度分布特征和多次方谱特征如仿真图3～7所示。从仿真图3～5上可以发现,对于OFDM子载波基带数字调制相(PSK)信号,幅度在理论值周围成正态分布;从图6和图7上可知,正交幅度调制(QAM)基带信号幅度会在多个理论值周围成正态分布;因此,可以提取这个特征以实现PSK与QAM信号的分类。

(a) BPSK无频偏星座图(a) BPSK no-CFO constellation graph

(b) BPSK归一化频偏0.01星座图(b) BPSK normalized CFO is 0.01 constellation graph

(c) BPSK幅度分布(c) BPSK amplitude distribution

(d) BPSK二次方谱(d) BPSK square spectrum图3 载波频率偏差条件下BPSK信号幅度分布特征和多次方谱特征仿真图Fig.3 Simulation diagram of amplitude distribution characteristics and multiple square spectrum characteristics of BPSK signal under carrier frequency deviation

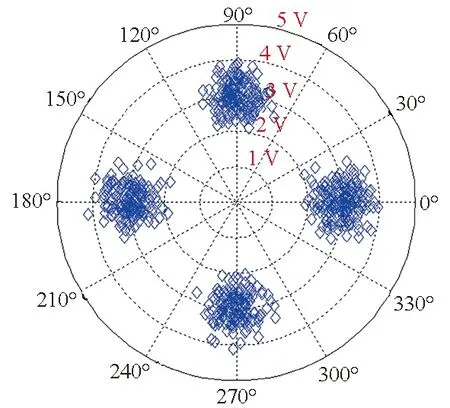
(a) QPSK无频偏星座图(a) QPSK no-CFO constellation graph

(b) QPSK归一化频偏0.01星座图(b) QPSK normalized CFO is 0.01 constellation graph

(d) QPSK四次方谱(d) QPSK quartic spectrum图4 载波频率偏差条件下QPSK信号幅度分布特征和多次方谱特征仿真图Fig.4 Simulation diagram of amplitude distribution characteristics and multiple square spectrum characteristics of QPSK signal under carrier frequency deviation

(b) 8PSK归一化频偏0.01星座图(b) 8PSK normalized CFO is 0.01 constellation graph

(c) 8PSK幅度分布(c) 8PSK amplitude distribution

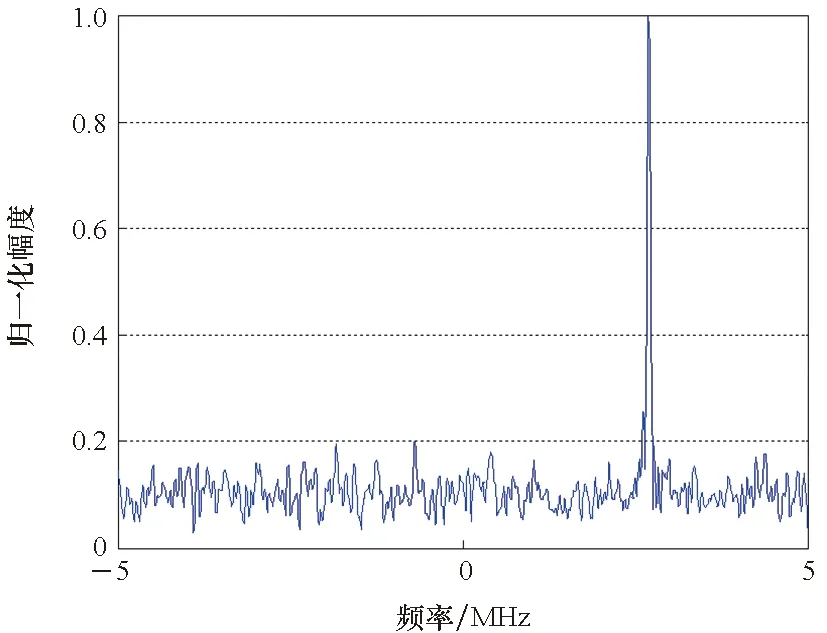
(d) 8PSK八次方谱(d) 8PSK 8th power spectrum图5 载波频率偏差条件下8PSK信号幅度分布特征和多次方谱特征仿真图Fig.5 Simulation diagram of amplitude distribution characteristics and multiple square spectrum characteristics of 8PSK signal under carrier frequency deviation

(a) 8QAM无频偏星座图(a) 8QAM no-CFO constellation graph

(b) 8QAM归一化频偏0.01星座图(b) 8QAM normalized CFO is 0.01 constellation graph

(c) 8QAM幅度分布(c) 8QAM amplitude distribution

(a) 16QAM无频偏星座图(a) 16QAM no-CFO constellation graph

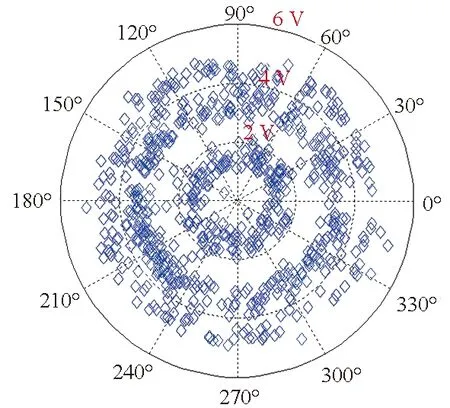
(b) 16QAM归一化频偏0.01星座图(b) 16QAM normalized CFO is 0.01 constellation graph

(c) 16QAM幅度分布(c) 16QAM amplitude distribution

(d) 16QAM二次方谱(d) 16QAM square spectrum图7 载波频率偏差条件下16QAM信号幅度分布特征和多次方谱特征仿真图Fig.7 Simulation diagram of amplitude distribution characteristics and multiple square spectrum characteristics of 16QAM signal under carrier frequency deviation

另外,PSK调制类内部的调制阶数M与其对应的M次方谱具有的相关性,在仿真图中也得到了验证,所以可以依据这个特征识别其调制阶数M。

对于QAM类内部调制阶数M,除了与其幅度分布情况有对应关系,还与其对应的多次方谱特征具有的相关性,以此可识别QAM信号的调制阶数。

4.2 仿真实验2:调制识别率对比仿真分析

仿真参数与仿真实验1相关设置一致。

将中频数据的每一帧基带信号加入归一化频偏0.01后,作为识别算法的输入。每帧单独识别其调制,每仿真一次计算它们的识别率,每种调制进行500次蒙特卡罗仿真,每一次仿真数据中大约包含157个完整数据帧。算法各调制样式的识别率如图8所示。从图8可以看出,本文识别方法在有CFO条件下,信噪比≥5 dB时,对各调制样式的识别率基本在90%以上,由于8PSK调制用到八次方谱,所以对信噪比的适应能力稍差一些。

图8 载波频率偏差条件下本文算法对各调制的识别率Fig.8 Recognition rate of the paper algorithm with CFO

统计本文算法对PSK类信号的平均识别率,并与文献[19]用基于高阶累积量的方法以及文献[20]基于循环平稳特性识别方法进行对比,如图9～10所示。从图9和图10可以看出,本文算法在无载波偏差和有载波偏差条件下,识别率都要优于高阶累积量和循环平稳特性方法。

(a) 无载波频率偏差(a) Without CFO

(b) 有载波频率偏差(b) With CFO图9 无载波频率偏差和载波频率偏差条件下PSK识别算法对比情况Fig.9 Comparison of PSK recognition algorithms without CFO and with CFO

(a) 无载波频率偏差(a) Without CFO

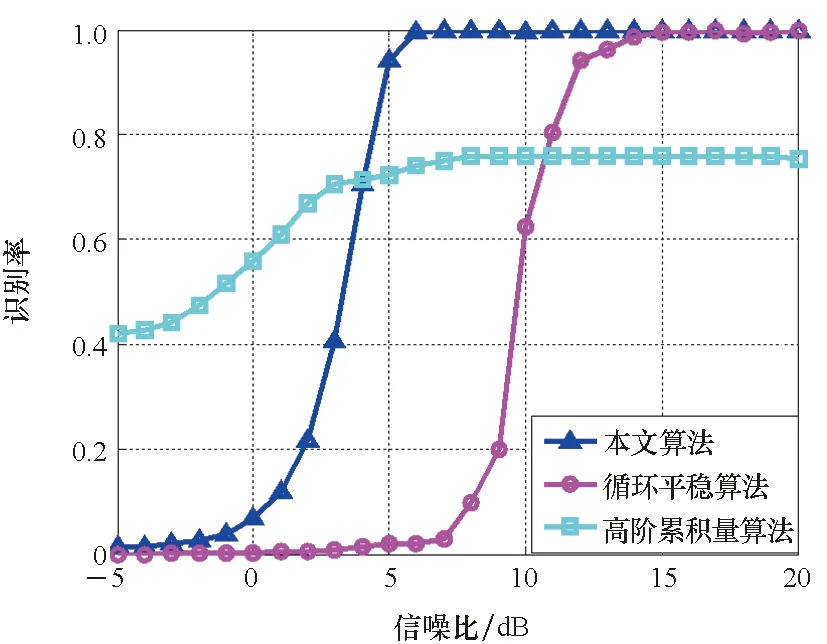
(b) 有载波频率偏差(b) With CFO图10 无载波频率偏差和有载波频率偏差条件下QAM识别算法对比情况Fig.10 Comparison of QAM recognition algorithms without CFO and with CFO

4.3 仿真实验3:CFO适应性对比仿真分析

为了验证算法对CFO的适应能力,设置了如下仿真条件:归一化频率偏差变化范围为0～0.02,间隔0.002,其他参数设置参照仿真实验1。算法识别率随载波频率偏差变化曲线如图11所示,从图11可以看出,当CFO小于0.01时,三种算法的识别率都在90%以上,当CFO逐渐增加至0.02时,循环平稳方法和高阶积量方法识别率出现较大恶化,而本文算法依然保持较好的识别率。

图11 算法识别率随载波频率偏差变化曲线Fig.11 Variation curve of algorithm recognition rate with CFO

4.4 仿真实验4:算法时间复杂度仿真分析

为了分析算法的时间复杂度,设置了如下仿真条件:信号的码片数范围为100～2 100,间隔200,其他参数设置参照仿真实验1。算法时间复杂度随码片数变化曲线如图12所示,从图12可以看出,随着码片的增加,本文算法与高阶累积量算法的时间复杂度基本保持一致,而循环平稳算法的时间复杂度会显著增加。

图12 算法时间复杂度随码片数变化曲线Fig.12 Variation curve of algorithm time complexity with chip number

5 结论

针对多载波OFDM信号子载波调制识别问题,本文提出了一种基于信号幅度分布特征和多次方谱线特征相结合的调制样式识别算法。该算法通过直方图统计幅度分布,并采用卡尔曼滤波对分布曲线去噪,提高了对信噪比的适应能力。通过仿真证明了本文提出的识别算法相比高阶累积量的算法具有较好的抗载波频率偏差能力,在CFO条件下,提高了调制识别率;相比循环平稳算法具有更好的噪声适应能力,相同的识别率下,能适应更低的信噪比。