RCS特性辅助的CMIMO雷达功率资源分配方法*

杨庆伟,蒋李兵,郑舒予,丁 瑞,王 壮

(国防科技大学 电子科学学院 ATR重点实验室, 湖南 长沙 410073)

近年来,空中探测环境日趋复杂,为应对雷达探测突防,各型作战目标层出不穷,这对防空预警雷达的多目标跟踪能力提出严峻挑战[1]。集中式多输入多输出(collocated multiple input multiple output,CMIMO)雷达作为一种新体制雷达[2-4],通过发射波形分集的手段,使不同发射波束指向多个目标,能够实现空中目标的同时多波束探测,其克服了传统相控阵雷达分时跟踪的缺点,在多目标检测跟踪、参数估计及抗干扰等领域应用广泛。现代雷达目标跟踪环境复杂多变,雷达系统设计愈发复杂,雷达跟踪资源分配问题已然成为一个非常有实际应用价值的研究课题。目标雷达散射截面(radar cross section, RCS)是雷达对目标探测与跟踪的重要参数之一[1],如何有效利用目标先验散射特性信息,实现雷达有限发射资源的精准分配,对合理配置雷达资源,提升CMIMO雷达多目标跟踪性能与精度具有重要的研究价值。

现阶段,在雷达资源调度方面已经形成一些研究成果。Garcia团队[5-6]针对多目标探测跟踪情形,开展了多输入多输出(multiple-input multiple-output,MIMO)雷达参数的选择优化问题研究。严俊坤等[7-8]基于克拉美罗下界(Cramer-Rao lower bound, CRLB)理论建立了基于贝叶斯克拉美罗下界[9]的代价函数,利用梯度投影算法,得到了在不同运动参数下雷达系统对多目标跟踪的功率最优分配结果[7-9]。Zhang等[10-11]针对分布式MIMO雷达与集中式MIMO雷达两种体制构型,分别研究了面向空中目标跟踪的资源分配方法,以多批目标跟踪的后验克拉美罗下界(posterior Cramer-Rao lower bound, PCRLB)之和为依据,实现雷达功率分配。在PCRLB理论[12]基础上,易伟团队[13-14]针对MIMO雷达多目标跟踪资源分配问题,研究了可供差异化的跟踪资源调度方案,综合考虑系统约束与外部因素,提出了联合功率波束分配方法,实现了全局目标函数设计与求解[12-14]。李正杰等[15-16]分别针对RCS非起伏场景与RCS起伏模型研究了CMIMO雷达的功率分配方案,验证了功率优化分配算法有效性。然而上述研究与算法仍然存在局限性,绝大部分成果只是把目标当成RCS非起伏模型或者给予简单的时变特征,仅重点考虑了目标运动参数对跟踪精度的影响。

在实际的雷达系统探测跟踪场景中,雷达观测视线角度对目标RCS特性影响甚大。具体表现为,在整个跟踪过程中,目标的多帧RCS数据呈现高动态起伏特征[17-19]。但是现有的雷达跟踪资源调度并没有将目标的动态RCS特性考虑在内,这就导致以往的雷达资源分配方案并不能完全适配于实际的探测场景,最终出现跟踪发散甚至失跟现象。另外,对于雷达系统而言,往往会不断地构建并扩大目标信息库,目的是利用目标信息库对不同的目标采用有针对性的信息处理方案,这就指导分配过程需要将目标特性考虑到实际的目标跟踪过程当中,以此形成更加适配于实际跟踪过程的雷达资源分配方案。

受此启发,提出了一种基于目标高动态RCS特性的CMIMO雷达功率自适应分配算法,目的是在多目标高动态RCS探测跟踪场景中合理分配CMIMO雷达有限的功率资源。

1 空中目标观测系统建模

1.1 目标运动模型

图1为CMIMO雷达对空中目标的同时多波束观测示意图,雷达在可观测范围内对目标进行持续探测跟踪。

图1 雷达同时多波束观测示意图Fig.1 Radar simultaneous multi-beam observation

假设在场景中存在Q个彼此分离的跟踪目标,并假定它们做匀速直线运动,则第k时刻第q个目标的运动模型可以被定义为:

(1)

(2)

(3)

⊗表示Kronecker积;ΔT表示相邻跟踪时刻的帧间时间间隔;I2表示二阶单位矩阵。

(4)

其中,eq是用来控制过程噪声协方差大小的过程噪声系数。

1.2 CMIMO雷达量测模型

设探测雷达体制为CMIMO雷达,其坐标为(x0,y0),将雷达的全部回波信号进行脉冲压缩、动目标检测等预处理后,形成一系列雷达量测。在k时刻,雷达对Q个彼此独立的目标进行跟踪,第q个目标的观测向量和目标状态向量的关系为

(5)

其中,vq,k～N(0,Ξq,k)为系统的量测噪声,hq,k(·)为目标q在k时刻其状态信息从目标状态空间到雷达量测空间的映射过程,包含目标距离、速度与角度信息,其向量形式为

hq,k(·)=[Rq,k(·),fq,k(·),φq,k(·)]T

(6)

其中,系统的三维量测分别表示为

(7)

其中,λ为雷达工作波长。

系统量测噪声vq,k～N(0,Ξq,k)的协方差矩阵表示如下

(8)

(9)

在雷达发射资源有限的情况下,研究不同目标RCS特性情况下的雷达功率需求机制,将多目标散射截面动态序列作为先验加入目标实时跟踪场景,显然能够提升最终雷达功率分配方案与实际跟踪场景适配性,对有效提升CMIMO雷达的多目标跟踪精度与效能具有核心支撑作用。

1.3 雷达观测下的静态RCS数据库构建与动态RCS数据序列映射

在目标动态RCS序列映射之前,首先需要采用物理光学(physics optics,PO)法获取目标全方位静态RCS数据库。利用电磁计算软件对跟踪场景中的多个目标完成建模,并在全空域范围内得到误差较小、相对合理的RCS值,从而完成对典型目标静态RCS数据库的建立。考虑到大多数目标均为对称结构,约定俗成地规定雷达入射方位角的取值范围为0°～180°,方位角为0°表示机头方向,方位角为180°则表示机尾方向。

图2为典型目标全方位RCS与雷达观测几何关系示意图。

图中给出雷达站心直角坐标系、目标坐标系的定义以及雷达视线(line of sight, LOS)。雷达站心坐标系XOY固定于雷达之上,其坐标原点位于雷达位置,X轴指向水平面正东方向,Y轴则指向当地水平面正北方向。目标坐标系XTOTYT则固定于目标之上,以目标中心为坐标原点,其YT轴平行于机身轴线并指向目标航向,XT轴垂直于YT轴。雷达指向目标中心的方向即为雷达视线LOS。

在此基础上,本节说明了坐标系间的转换关系,获得静态RCS数据库、雷达视线与动态RCS序列的映射关系,从而在实际作战中通过获取的动态RCS序列指导雷达多目标功率分配,提升多目标跟踪精度。

(10)

β=180°-α

(11)

α与β的取值范围均为[0°,180°],β角即可确定雷达在跟踪过程中目标相对入射角与动态RCS序列的数据映射过程。

于是,在实际跟踪过程中目标动态RCS序列映射流程如图3所示。

图3 目标动态RCS序列映射流程Fig.3 Dynamic RCS sequence mapping process

2 多目标跟踪PCRLB递推式

考虑到实际的目标探测过程中,雷达发射总功率受限,不同运动目标会处于监视区域的不同位置,随着目标到雷达的距离以及其他诸如角度不同导致的目标RCS变化,雷达对目标的探测性能也随之改变。根据实时跟踪环境与目标运动状态对多目标跟踪环境进行精确感知与合理的资源调度,能充分发挥雷达系统的多目标跟踪性能。

用所建立量测模型的量测值对目标状态向量进行估计时,其无偏估计量与目标状态向量之间须满足

(12)

(13)

(14)

(15)

(16)

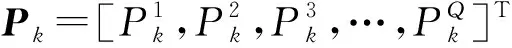
3 功率分配优化算法

3.1 功率分配优化模型

当前观测系统的非线性程度较高,传统的卡尔曼滤波与扩展的卡尔曼滤波算法无法有效消除滤波跟踪的发散问题,因此采用无迹卡尔曼滤波算法进行处理,能够很好地平衡非线性估计过程中的精度问题与工程实现的问题。由第2节可知,目标跟踪精度的理论下界PCRLB受雷达发射功率以及目标RCS变化的影响。算法采用最小化最大PCRLB(Min-Max PCRLB)优化准则,讨论在CMIMO雷达发射功率受限以及目标动态RCS序列可预测情况下,对各个目标发射波束的功率分配问题,从而合理规划CMIMO雷达功率分配数值,优化多目标跟踪精度。

Min-Max PCRLB优化模型可以建模为

(17)

3.2 优化模型求解

3.1节的优化问题旨在CMIMO雷达功率存在约束条件、多目标RCS呈现高动态变化的情况下尽可能地提升系统的多目标跟踪精度。可以看出,上述优化问题是典型的多元函数有约束极值优化问题,其不等式约束构成可行域空间,利用内点算法构造内点惩罚函数,通过启发式算法实现RCS极化方式选取,即可利用序列迭代点在可行域内不断趋于符合约束的最优点。其完整的流程图如图4所示。

图4 基于动态RCS的雷达功率自适应分配流程图Fig.4 Radar power adaptive allocation flow chart based on dynamic RCS

总的来说,功率分配算法表述为:分配中心根据k-1时刻的目标运动状态,利用一步预测估计雷达对目标观测视线,选取合适的极化方式进行探测,利用内点法计算出k时刻各个目标的功率分配情况并进行反馈,从而自适应地调节各目标分配功率,完整算法如算法1所示。

4 仿真实验与分析

4.1 仿真实验参数

为验证基于动态RCS的CMIMO雷达功率分配算法的有效性,并进一步分析雷达发射参数与目标RCS对功率分配的影响,对二维空间中三个匀速运动的目标进行功率分配仿真实验。为直观体现所提算法能够有效解决功率分配方案与实际场景失配的问题,后续实验针对跟踪过程中目标RCS存在高动态起伏场景,对比动态RCS序列与传统RCS模型下跟踪实验结果,最后根据跟踪误差衡量不同功率分配方案的跟踪精度与效能。仿真实验设定雷达位置与基本参数如表1所示。

表1 雷达位置与基本参数Tab.1 Radar position and basic parameters

雷达对三个目标同时进行多波束跟踪,三个目标的初始运动参数如表2所示。在利用无迹卡尔曼滤波对三个目标分别进行跟踪的过程中,选定N=60帧数据进行仿真实验,雷达观测数据率为1 s,蒙特卡罗实验次数为100次。为直观地对比不同情况下雷达的多目标跟踪性能,并定量衡量各个目标的跟踪精度,通过计算各目标跟踪过程中的位置均方根误差(root mean square error, RMSE)数值与速度RMSE数值进行跟踪效果对比,对应公式分别为

表2 目标运动参数Tab.2 Target motion parameters

4.2 空中目标全静态RCS数据库

为得到一个相对完善的目标静态RCS数据库,对三个运动目标进行建模,并进行RCS数据仿真,考虑到一般雷达系统的同极化增益要远远大于交叉极化增益,因此对于每个目标分别采用水平同极化(horizontal-horizontal,HH)与垂直同极化(vertical-vertical,VV)的方式进行RCS仿真,结果如图5所示。

(a) 目标1静态RCS数据库(a) Static RCS database of target 1

(b) 目标2静态RCS数据库(b) Static RCS database of target 2

(c) 目标3静态RCS数据库(c) Static RCS database of target 3图5 多目标静态RCS数据库Fig.5 Static RCS database of multi-target

为了更加直观地对比三个目标分别在HH与VV两种探测方式下RCS的数值区别,本节构建了图6所示所有目标的RCS静态数据库,从图中能够明显看出,对于不同目标,其仿真RCS具有明显差异,且由于目标外形以及材料的差异,其RCS峰值区域也具有明显的角度分集特征。另外,对于同一目标,两种同极化方式下的RCS也存在一定差异,因此在目标跟踪的过程中,可以选取RCS较大的同极化方式,对目标进行跟踪处理。

图6 所有目标静态RCS可视化Fig.6 Visual results of all target static RCS

4.3 雷达多目标跟踪仿真实验

利用所提方法对三个目标进行了同时多波束跟踪处理,对应的跟踪预测结果如图7所示。根据探测雷达与目标相对运动过程中探测视角的变化,可以得到图8所示的动态RCS数据抽取结果。图9为跟踪期间三个目标对应的雷达极化方式的选择结果。可以看到,所提算法根据跟踪过程中的雷达视线实时变化,选取了RCS更大的极化方式进行跟踪。三个目标对应的动态RCS变化曲线如图10所示。

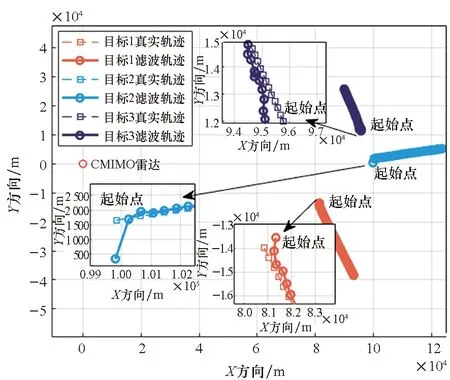
图7 三个目标跟踪结果Fig.7 Tracking results of three targets

图8 动态RCS序列对应观测方向角Fig.8 Dynamic RCS sequence corresponding to observation direction angles

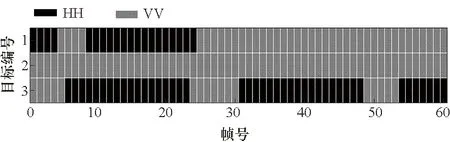
图9 极化方式选择结果Fig.9 Polarization selection results

图10 动态RCS数据变化曲线Fig.10 Dynamic RCS data changing curve

从图10可以看出,在整个跟踪过程中,不同目标的动态RCS具有明显差异。目标1与目标3的动态RCS变化范围较为接近,在整个跟踪过程中,目标1与目标3的动态RCS相互交错,而目标2的RCS则大于目标1与目标3的动态RCS。为了有效利用目标特性信息,需要结合跟踪过程中的实时动态RCS数据进行功率调度。

图11为整个跟踪过程中三个目标与探测雷达的距离变化曲线。从图中可以看出,在整个目标跟踪过程中,目标1与目标2沿着背离雷达的方向运动,其与雷达的距离随着观测时间的增大而增大;而目标3与雷达之间的距离则越来越小,在跟踪第31帧时,目标1与目标3距离雷达的距离接近。

图11 目标跟踪实时距离Fig.11 Dynamic range of targets tracking process

算法采用Min-Max PCRLB准则对三个目标进行功率动态分配。Min-Max PCRLB准则的目的为优化跟踪精度最差的目标,因此,三个目标的跟踪结果将越来越接近,在跟踪后期趋于一致。仿真实验所得功率分配理论值如图12所示。可以看出,雷达对目标的跟踪过程中,由于目标2与雷达的距离随着时间越来越大,且三个目标中目标2距离雷达最远,因此在跟踪后期分配给目标2的雷达功率最多。而由于目标1在跟踪前期对应RCS最小,为保证目标1跟踪精度,算法在跟踪前期分配给目标1的波束能量最大。另外,在第35帧左右,由于目标1、目标3与雷达的距离接近,而目标3的RCS动态数值小于目标1的RCS动态数值,此时雷达的功率分配趋势更趋向于目标3,相较于目标1而言,目标3所得功率短暂增加。可以看出,目标距离雷达远近与实时的动态RCS均为影响功率分配结果的重要因素。

图12 所提算法的功率分配结果Fig.12 Power allocation results of the proposed algorithm

图13与图14分别为三个目标跟踪过程中位置与速度的RMSE与PCRLB随跟踪帧号的变化曲线图。

图13 Min-Max PCRLB准则位置估计误差RMSE曲线Fig.13 RMSE curve of Min-Max PCRLB position estimation error

从图13可知,在雷达同时多波束目标跟踪过程中,当跟踪至第10帧数据时,三个目标的位置跟踪理论PCRLB数值明显下降。由于目标2的动态RCS最大,因此其理论PCRLB数值最小。由于目标3的动态RCS最小,其跟踪误差最大,但是由于算法采用Min-Max PCRLB准则进行多目标功率分配,因此目标3的跟踪精度并没有明显低于其余两个目标,三个目标的跟踪RMSE均逐渐收敛到PCRLB曲线,趋向于理论估计最优。

4.4 传统RCS起伏模型实验结果比较

为了对比不同RCS模型下的多目标跟踪精度,对Min-Max PCRLB优化准则下传统RCS起伏模型跟踪结果(文献[16]方法)与所提高动态RCS自适应功率分配的多目标跟踪结果进行比较。传统的RCS模型并没有结合雷达观测视线与目标运动信息,通过给予RCS较小的动态变化,模拟跟踪过程中多目标RCS起伏特性。图15为传统多目标RCS起伏模型。

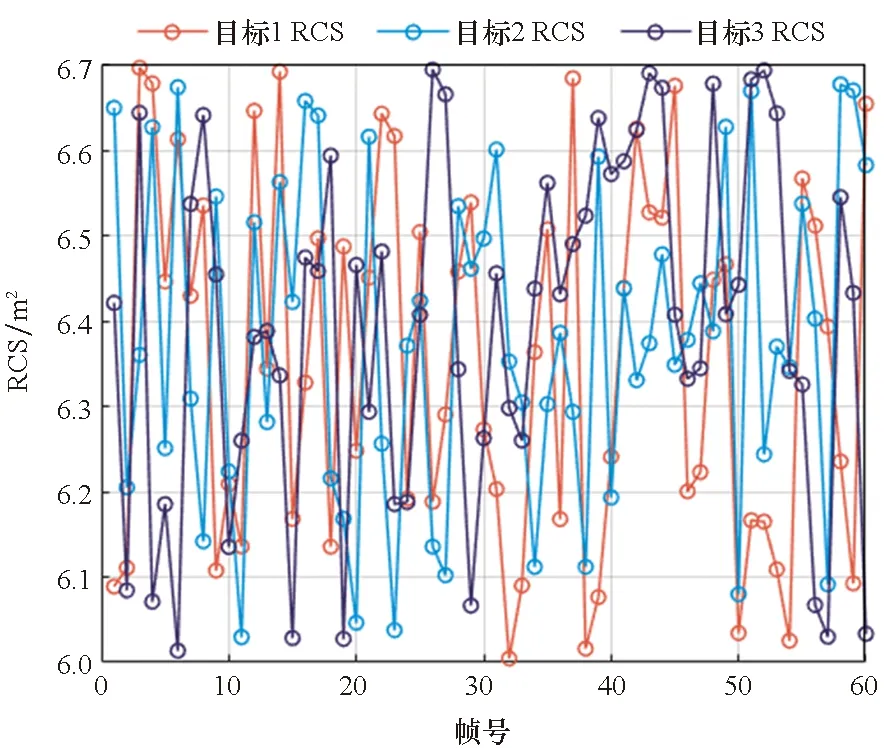
图15 传统RCS起伏模型曲线Fig.15 Traditional RCS fluctuation curve

图16为传统RCS起伏模型情况下三个目标跟踪过程中的功率分配结果。从图中可以看出,分配给三个目标的功率值自由度较差,在不同跟踪时刻,单个目标所得功率没有明显差异,这将导致在目标运动过程中,其跟踪误差出现发散甚至目标失跟的现象发生。

图16 传统RCS起伏模型的功率分配结果Fig.16 Power allocation results of traditional RCS fluctuation model

图17与图18分别为传统RCS起伏模型情况下三个目标跟踪过程中位置与速度的RMSE与PCRLB随跟踪时刻的变化曲线图。从图中可以明显看出,由于分配给目标2的雷达波束能量较低,在跟踪第5帧开始,其位置RMSE出现发散的现象,在跟踪后期,目标2距离雷达的距离最远,导致了雷达系统对目标2的跟踪性能较其余两个目标最差,且其速度RMSE收敛很慢,继续观测甚至会出现目标2失跟现象。可以看出,传统的RCS模型并不能有效结合多目标RCS动态变化过程,得到雷达功率的最优分配。

图17 起伏模型位置估计误差RMSE曲线Fig.17 RMSE curve of position estimation error of fluctuating model

图18 起伏模型速度估计误差RMSE曲线Fig.18 RMSE curve of velocity estimation error of fluctuating model

为了更加直观地展示所提算法效能,给出在动态RCS与传统RCS情况下多目标跟踪结果曲线对比图,其位置估计RMSE与速度RMSE分别如图19与图20所示。从图19中可以看出,所提算法中目标3的位置估计RMSE最大,在第59帧时,其位置RMSE数值为135.768 m,而传统RCS模型情况下,目标2与目标3的位置跟踪误差接近,对应RMSE为195.509 m。另外,还可以看出,在整个跟踪阶段,所提算法跟踪精度最差的目标位置RMSE始终小于传统算法,位置估计精度提升约30.77%。从图20可以看出,传统RCS模型算法中目标2的速度估计RMSE最大,在跟踪后期第51帧时,其数值为5.198 56 m/s。所提算法在跟踪前期目标2的速度估计RMSE最大,第35帧开始,三个目标的速度估计RMSE趋于一致,对应数值约为3.033 9 m/s。同样地,所提算法跟踪精度最差的目标速度RMSE始终小于传统算法,速度估计精度提升约42.31%。所提算法能够有效结合跟踪过程中多目标实时RCS动态特征,一定程度上提升了雷达系统的多目标跟踪性能。

图19 不同RCS模型下位置RMSE对比Fig.19 Comparison of position RMSE under different RCS model

图20 不同RCS模型下速度RMSE对比Fig.20 Comparison of velocity RMSE under different RCS model

4.5 算法实时性检验

所提算法优化问题等式约束与不等式约束共m=2个,优化变量为n=3个,完整算法的时间复杂度可以表示为:Ο(Ν(mn3+m2n2+m3+n3))。为检验所提算法实时性,本文开展了100次蒙特卡罗仿真实验,各帧优化时间结果如图21所示。可以看到,绝大多数跟踪帧的优化求解时间在0.05 s上下浮动,满足跟踪资源分配的实时性要求。

图21 各帧优化时长Fig.21 Optimization duration of each frame

5 结论

本文基于CMIMO雷达系统,提出一种符合实际多目标探测场景下目标高动态RCS的雷达功率自适应分配算法。通过雷达探测视线与多目标预测运动方向,获取不同极化方式下多目标的动态RCS,结合目标运动状态,联合指导CMIMO雷达功率分配。仿真表明,所提算法能够有效结合多目标RCS动态散射特性实现功率的有效分配,相比于传统RCS模型情况下的跟踪结果,通过构建RCS数据库能够有效结合目标运动特性与RCS散射特性,并进一步实现极化方式优选,提升了CMIMO雷达的多目标跟踪性能。需要指出的是,所提算法仅针对单雷达多目标探测场景,而在实际观测中,多部雷达组成的雷达组网情况有待进一步研究。