助数学思维发展 促核心素养提升
——以GGB在问题解决中的应用为例
浙江省湖州市南浔高级中学 (313009) 刘太杰 刘定勇
《普通高中数学课程标准(2017年版)》强调“信息技术是学生学习和教师教学的重要辅助手段,为师生交流、生生交流、人机交流搭建了平台,教师应注重信息技术与数学课程的深度融合,实现传统教学手段难以达到的效果.”.GeoGebra(简称GGB)作为一款集代数运算、几何作图、数据处理等于一体的动态数学软件在演绎思维的发展过程,助推思维的可感知、可发散、可视化,促进了核心素养的提升等方面发挥着日益重要的作用.
1 化繁为简让思维可感
案例1 已知函数f(x)=(|x-a|+b)·ln|x+a|,a,b∈R,若f(x)≥0在定义域上恒成立,则a-2b的值是( ).
A.-1 B.0 C.1 D.2
本题初看是含参恒成立问题,但由于参数较多,函数形式复杂,参变无法分离,但如果将函数f(x)分解为两个函数之积,分别考查它们的图像特征,便会豁然开朗.
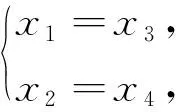
几何推演:GGB实验探究
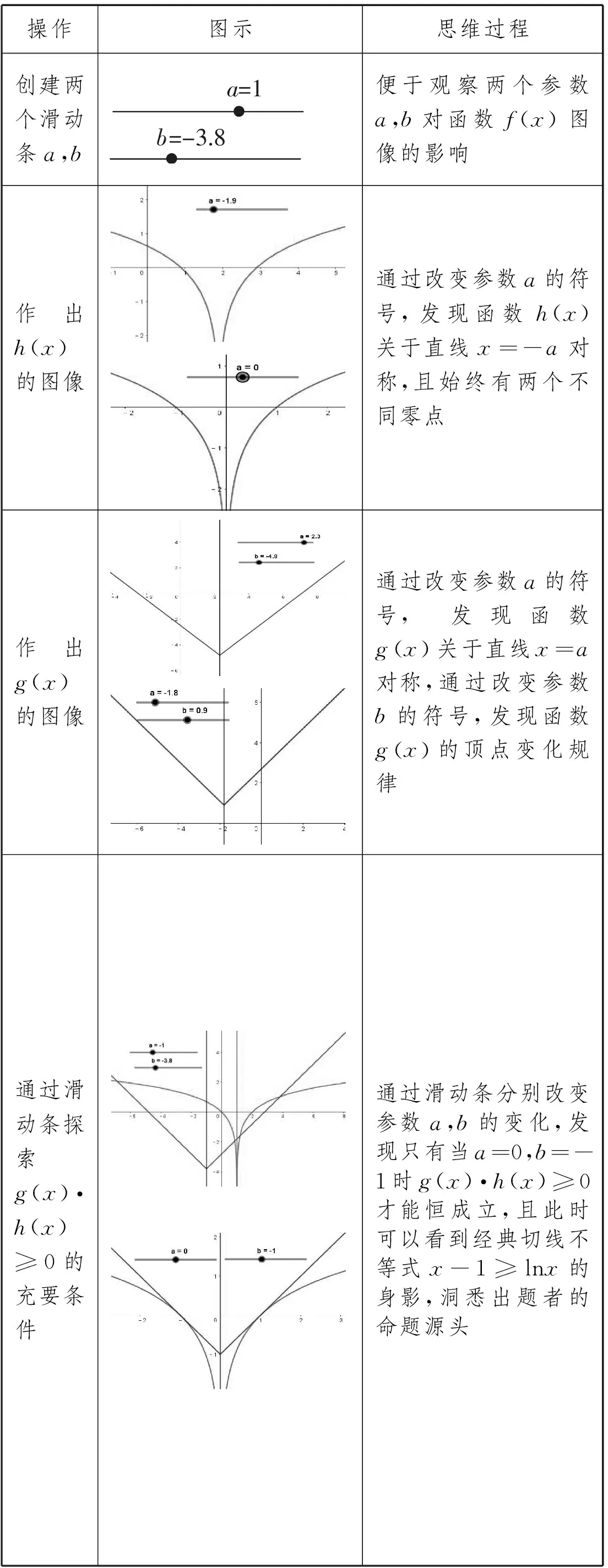
操作图示思维过程创建两个滑动条a,ba=1b=-3.8便于观察两个参数a,b对函数f(x)图像的影响作出h(x)的图像通过改变参数a的符号,发现函数h(x)关于直线x=-a对称,且始终有两个不同零点作出g(x)的图像通过改变参数a的符号,发现函数gx 关于直线x=a对称,通过改变参数b的符号,发现函数gx 的顶点变化规律通过滑动条探索g(x)·h(x)≥0的充要条件通过滑动条分别改变参数a,b的变化,发现只有当a=0,b=-1时g(x)·h(x)≥0才能恒成立,且此时可以看到经典切线不等式x-1≥lnx的身影,洞悉出题者的命题源头
类题演练:已知f(x)=(|x|+a2-1)·ln|x+a|,a,b∈R,若f(x)≥0在定义域上恒成立,则a+b的值是________.
反思品味:对于上述复杂的含参函数恒成立问题,GGB展示了它在探索思路、展示图像、发现源头、让思维可感知等方面发挥的巨大作用,让抽象的函数问题变得形象起来,让学生感知到思维的发展过程,为问题的解决指明了捷径,提升了建模、推理、分析等素养.
2 另辟蹊径促思维发散
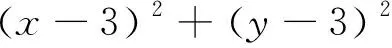
思路探求:易知点P不但在圆C上,而且在以AB为直径的圆上,于是可以联想到两圆的位置关系求解,此外,我们还可以从圆的参数方程、直线与圆的位置关系、GGB作图分析临界位置等方面入手处理.
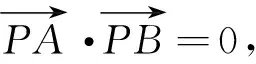
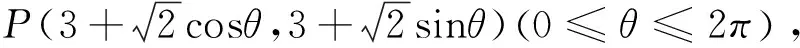
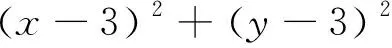
几何推演:GGB实验探究
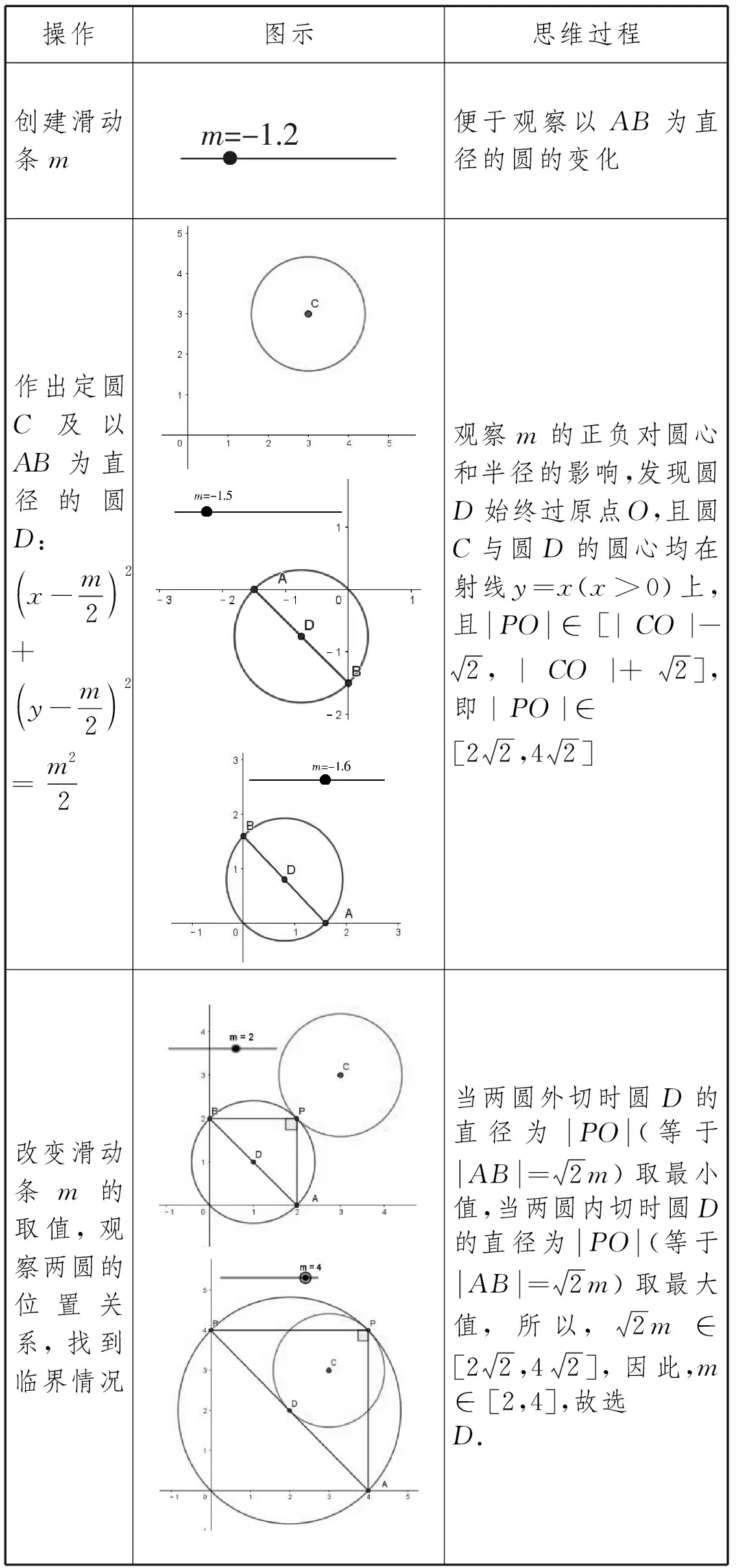
操作图示思维过程创建滑动条mm=-1.2便于观察以AB为直径的圆的变化作出定圆C及以AB为直径的圆D:x-m2 2+y-m2 2=m22观察m的正负对圆心和半径的影响,发现圆D始终过原点O,且圆C与圆D的圆心均在射线y=x(x>0)上,且PO∈[|CO|-2,|CO|+2],即|PO|∈[22,42]改变滑动条m的取值,观察两圆的位置关系,找到临界情况当两圆外切时圆D的直径为PO(等于AB=2m)取最小值,当两圆内切时圆D的直径为PO(等于AB=2m)取最大值,所以,2m∈[22,42],因此,m∈[2,4],故选D.
类题演练:(多选题)已知点A(u+2,0),B(-u,0),若圆C:(x-4)2+(y-4)2=9上存在唯一的点P,使得PA⊥PB,则u的值可能为( ).
A.-9 B.-5 C.1 D.7
3 绘形绘色助思维可视
案例3 球体在工业领域有广泛的应用,某零件由两个球体构成,球O1的半径为10,P,Q为球O1表面上两动点,PQ=16,M为线段PQ的中点.半径为2的球O2在球O1的内壁滚动,点A,B,C在球O2表面上,点O2在截面ABC上的投影H恰为AC的中点,若O2H=1,则三棱锥M-ABC体积的最大值是________.
分析:本题的难点在于空间图形的位置理解与条件转化,通过GGB的3D作图功能可以将抽象的问题具体化、形象化,有助于加深对问题的认识与理解.
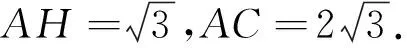
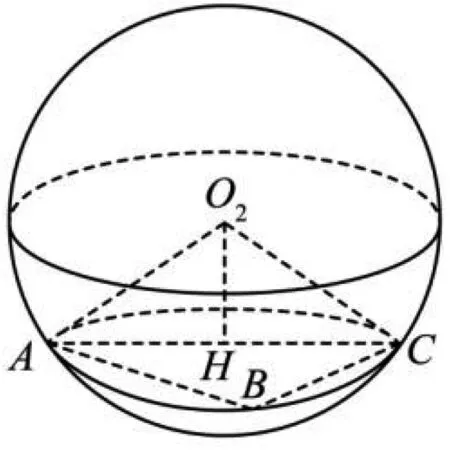
图1
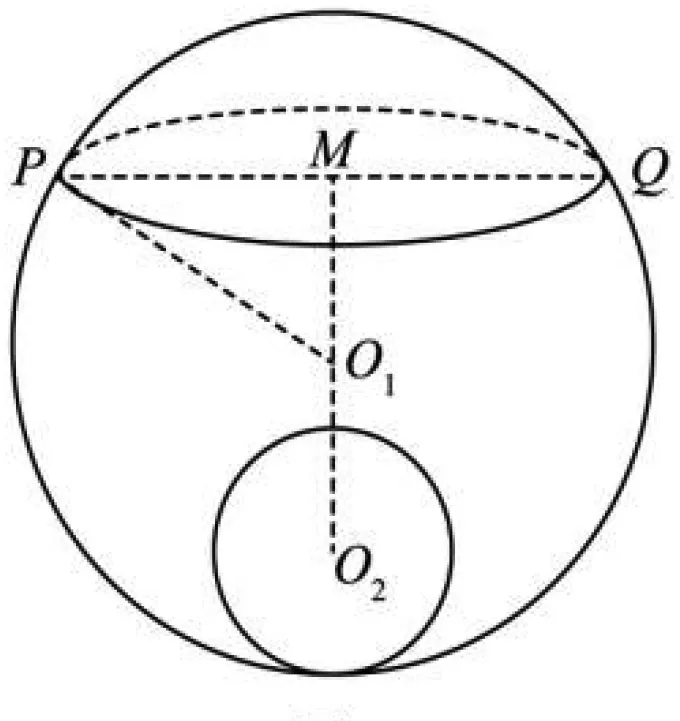
图2
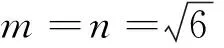
GGB实验:(动态立体演示)
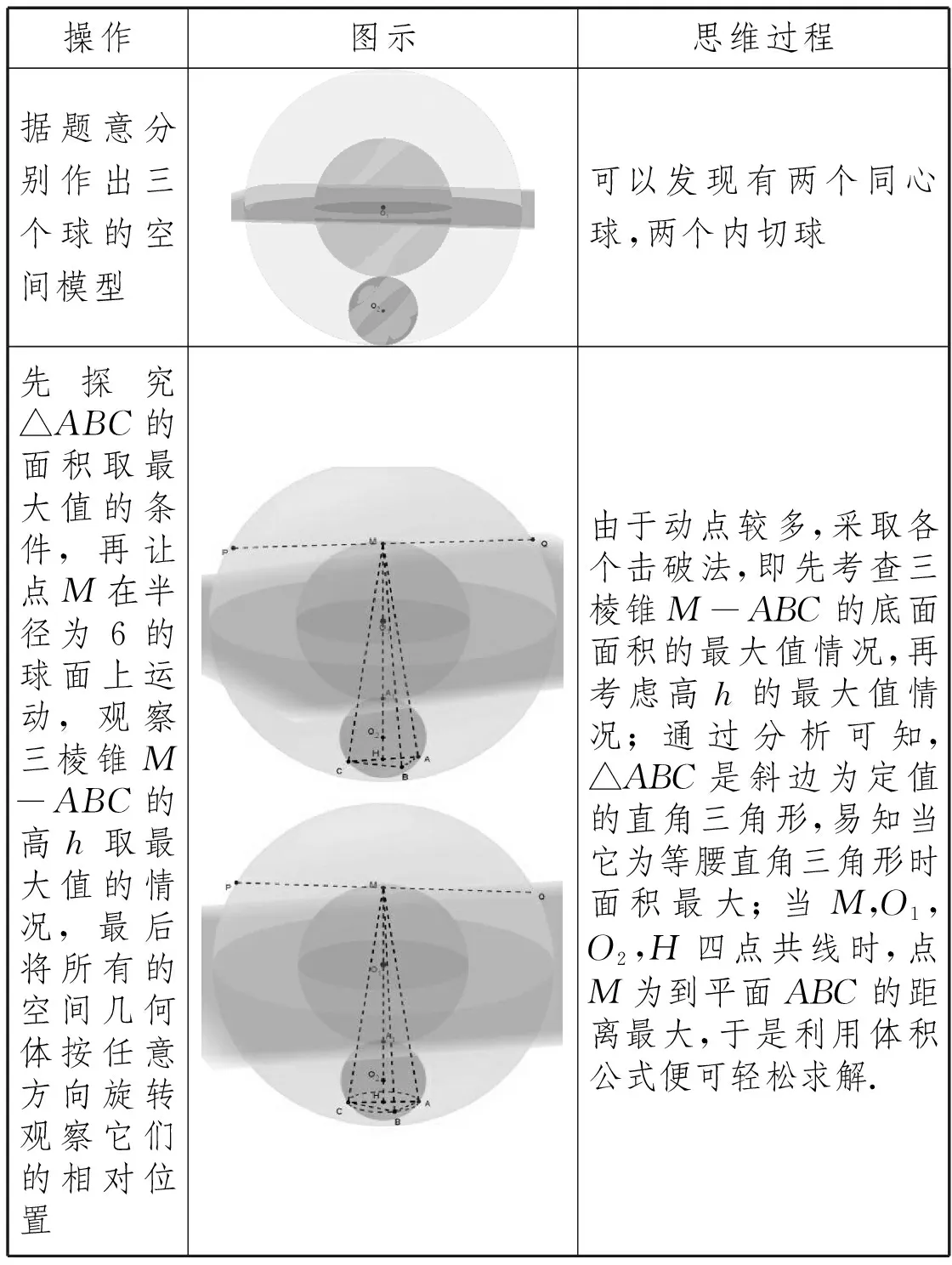
操作图示思维过程据题意分别作出三个球的空间模型可以发现有两个同心球,两个内切球先探究△ABC的面积取最大值的条件,再让点M在半径为6的球面上运动,观察三棱锥M-ABC的高h取最大值的情况,最后将所有的空间几何体按任意方向旋转观察它们的相对位置由于动点较多,采取各个击破法,即先考查三棱锥M-ABC的底面面积的最大值情况,再考虑高h的最大值情况;通过分析可知,△ABC是斜边为定值的直角三角形,易知当它为等腰直角三角形时面积最大;当M,O1,O2,H四点共线时,点M为到平面ABC的距离最大,于是利用体积公式便可轻松求解.
4 反思与展望
本文以GGB在问题解决中的应用为例,从可感知、可发散、可视化等方面探索了它在演绎思维的过程、助推思维的发展、促进核心素养的提升等方面发挥的重大作用.
GGB在教学与科研中的应用日益广泛,在辅助日常教学时能够启发学生思维、简化运算过程、增加课堂灵动性.

