基于傅里叶级数的钢筋桁架楼承板振动控制方法
陈俊言,姚伟豪,王立欢,符修育,林贵鹏
(1.中建二局第一建筑工程有限公司,北京 100000;2.中国建筑第二工程局有限公司,北京 100000)
1 引言
傅里叶级数是一种特殊的三角级数, 其在任意一个数值周期内的函数关系都可以表示为正弦或余弦函数, 且无穷级数指标之间的基函数正交关系也始终不会发生变化。 根据欧拉公式推导原则可知, 三角函数可以被直接转化为指数表达式,所以,傅里叶级数也是一种符合数值变化规律的指数级数条件[1]。 在函数值附属区域内,傅里叶级数指标的求解要求两个不同向量的内积结果必须等于零, 这就意味着除了空间相交关系外,这两个向量参数之间没有其他相关性。
钢筋桁架楼承板是指由钢筋桁架和底板组合而成的承重板结构,为保证结构体系的抗压能力,底板与钢筋桁架之间主要通过电阻点焊的方式进行连接。 钢筋部分包括上弦、下弦、腹杆,其中,上弦是指最上端各节点之间的连接杆件;下弦则是指最下端各节点之间的连接杆件;腹杆是指存在于上弦、下弦部件之间的过渡杆件结构。 随着楼层高度的不断增加,钢筋桁架楼承板所负担的力学载荷作用也在不断增大, 这就会导致楼承板出现形变量, 并最终造成楼体坍塌。 为解决上述问题, 本文针对基于傅里叶级数的钢筋桁架楼承板振动控制方法展开研究。
2 钢筋桁架楼承板的载荷模型
对于钢筋桁架楼承板载荷模型的求解是实现对其振动行为有效控制的基础环节,本文将在傅里叶级数指标的支持下,建立非齐次波动方程, 再联合其他参数向量确定具体的载荷动力条件。
2.1 傅里叶级数指标
求解傅里叶级数指标需要分别定义获取的数据样本的值域与频域特征,并根据数据级数展开条件,判断当前求解结果是否符合实际应用需求[2]。 对于钢筋桁架楼承板结构,傅里叶级数指标可以作为判别振动特征是否具有可控性特征的基本数值条件,因此,为实现对其振动行为的有效控制,应精准定义傅里叶级数指标的具体取值范围。
设α为一个随机选取的数据样本参量,且α>1 的不等式取值条件恒成立;i为级数展开条件的最小取值结果;为数据样本的值域特征;为数据样本的频域特征;β为频域判别参数,联立上述物理量,可将傅里叶级数指标计算结果pα表示为:
若所选择数据样本参量具有明显对称性, 则表示傅里叶级数指标计算结果也具有明显对称性, 若求解所得参数只保持单向性特征, 则表示当前求解原则不能适应傅里叶级数指标的构建原则。
2.2 非齐次波动方程
非齐次波动方程是以傅里叶级数指标为基础建立的方程参考条件。 求解钢筋桁架楼承板力学载荷作用时,非齐次波动方程表达式既决定了参与计算指标参量的取值范围, 也对载荷模型的有效性提出了更高的要求。 所谓非齐次,是指参数指标的取值可以不属于同一数值区间, 将其对应在钢筋桁架楼承板载荷模型中, 则可以理解为载荷向量可以不属于同一受力平面, 即相同或不相同平面内的载荷系数只要满足同一傅里叶级数指标求解原则, 都可以被同一个非齐次波动方程定义[3]。设φ为基于傅里叶级数指标求解原则的力学载荷向量取值参数;q'为非齐次参考项;为所选力学载荷向量的波动特征。 在上述物理量的支持下,联立公式(1),推导基于傅里叶级数的力学载荷系数非齐次波动方程W表达式为:
在实际应用过程中, 钢筋桁架楼承板结构所承担的力学载荷作用强度不可能为零, 故而非齐次波动方程的求解结果也就不可能等于零, 这就是楼承板结构在较小压力形变情况下不会发生变形的主要原因。
2.3 载荷动力条件
载荷动力条件就是指能够导致楼承板出现形变的压力作用条件,一般来说,在默认不发生明显形变量的情况下,可以认为载荷动力条件的取值越大,表示钢筋桁架楼承板所承担的力学负载量越大。 对于钢筋桁架楼承板结构而言,施加在某一固定位置处的力学作用具有明显可传导的能力, 这就表示随着力学负载作用行为发生变化, 楼承板表面可能会出现载荷分布不均匀的情况, 而载荷动力条件的存在恰好解决了上述问题, 该项应用条件规定一定程度内的载荷不均匀分布只会影响力学负载的作用能力, 并不会造成明显的楼承板形变问题[4]。因此,在控制由形变作用引起的楼承板振动行为时,只要求力学负载作用数值处于可控范围内, 就可以根据傅里叶级数指标与非齐次波动方程之间的关联特性, 完成对实际载荷数值的精准求解。
3 振动行为控制
在傅里叶级数载荷模型的基础上, 计算钢筋桁架楼承板的调谐质量阻尼器(TMD)参数、深度系数与广度系数,就可以实现对楼承板结构振动行为的有效控制。
3.1 TMD参数
TMD 参数描述了钢筋桁架楼承板结构在外部载荷作用下所表现出的弹性力学振动能力。 对于弹性力学作用的理解,可以类比为一个悬挂在固定结构之上的弹簧元件, 随着力学作用等级的增大,弹簧元件虽然会出现形变量,但由于其自身具有回弹能力,所以,只要表现时间足够长,已发生形变的弹簧会再次恢复至初始状态[5]。钢筋桁架楼承板的弹性形变能力就是指随着外部载荷作用强度的增大, 楼承板结构所表现出的形变量虽然会增大, 但这种形变量却提供了一定的减振作用, 而这种减振效果也可以在一定程度上抵消外部所施加的负载作用, 进而实现减小振动响应的目的。 对于TMD 参数r的求解公式为:
式中,φ为弹性形变参数;k为抗力行为向量;g为承力行为向量。 钢筋桁架楼承板结构所具有的弹性复原能力有限,所以,TMD 参数指标的计算结果也可能无限大。
3.2 深度系数
深度参数是指钢筋桁架楼承板结构受力作用在纵深方向上的表现能力,其取值越大,表示力学载荷在纵深方向上的作用能力越强。 从宏观角度来看,纵深方向上力学作用会导致钢筋桁架楼承板结构出现横向断裂行为, 由于外部负载力的作用强度会随着楼承板厚度的增加而不断减小,所以,确保深度系数指标的取值足够小, 才有可能对钢筋桁架楼承板的振动表现行为进行有效控制[6]。设γ为钢筋桁架楼承板结构的横向断裂系数,f为力学负载作用在纵深方向上的物理分量。 在上述物理量的支持下,联立公式(3),推导深度参数d计算式为:
如果钢筋桁架楼承板的纵深断裂行为在到达某一深度水平后不再向下延伸, 则表示当前情况下外部载荷的力学作用得到完全发挥。
3.3 广度系数
广度系数是指钢筋桁架楼承板结构受力作用在水平方向上的表现能力,其取值越大,表示力学载荷在水平方向上的作用能力越强。 水平方向上的力学作用可以同时导致钢筋桁架楼承板的纵向与横向断裂行为,但前者的表现能力更强。 与纵深方向上的外部负载力作用不同, 水平负载力作用能力不会随着楼承板直径的增大而减小,所以,只要保持广度系数处于既定数值范围之内, 就有可能实现对钢筋桁架楼承板振动表现行为的有效控制。 求解广度系数l的公式如下:
式中,h为力学负载作用在水平方向上的物理分量;X为楼承板受力面的宽度数值。 为解决因力学载荷作用过大造成的楼承板振动问题,应同时参考TMD 参数、深度参数与广度系数。
4 实例分析
单位面积上的力学载荷作用会导致楼承板出现物理形变, 而这种形变量就是造成钢筋桁架楼承板出现振动行为的主要原因。 本次实验以屈服强度在330~380 MPa 的楼承板作为实验材料,在材料密度较为均匀的区域内,截取一块面积为1 m2的板材结构作为实验对象,分别施加1.0×109N、2.0×109N、3.0×109N、4.0×109N、5.0×109N 五种不同的作用力,记录在不同作用力情况下楼承板的具体形变量(规定形变量不超过5×10-5mm,力学载荷作用都不会导致楼承板结构出现明显振动行为),如图1 所示。
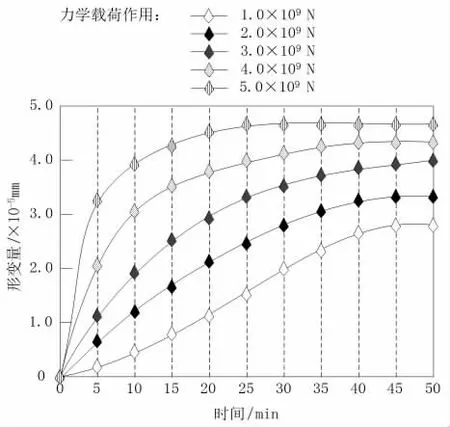
图1 钢筋桁架楼承板形变量
分析图1 可知,随着力学载荷作用强度的增大,钢筋桁架楼承板形变量均值会出现不断增大的变化态势, 但其最大值始终没有达到5×10-5mm,表示本次实验所选择的力学载荷作用强度不会导致楼承板结构出现明显振动行为。
5 结语
基于傅里叶级数的钢筋桁架楼承板振动控制方法利用非齐次波动方程,推导载荷动力条件,又根据TMD 参数、深度参数、广度系数的取值范围,对楼承板结构在力学载荷作用下表现出来的振动行为进行有限控制。 随着这种新型控制方法的应用,楼承板结构在力学载荷作用达到5.0×109N 的情况下也不会出现明显形变, 能够较好地解决因力学载荷作用过大造成的楼承板振动问题,符合实际应用需求。 未来相关组织机构可以针对傅里叶级数指标进行继续改进, 在提升钢筋桁架楼承板结构承力稳定性的同时,避免板材振动的出现,从而最大化提升楼承板的应用安全性。

