平抛运动解题方法谈

赵小勇

【摘要】高考考查中，常将平抛运动与体育运动、生活实际密切结合，结合三则例题，分析解决这一类问题的方法，以提高学生的解题能力.

【关键词】平抛运动；等时性；对称性；可逆性

平抛运动与我们的生活息息相关.高考考查中，常将其与体育运动、生活实际密切结合，以下结合例题对解决这一类问题的主要方法进行分析探讨.

1 利用平抛运动的特点

将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动，利用运动的等时性比较初速度大小、水平位移大小和竖直位移大小[1].

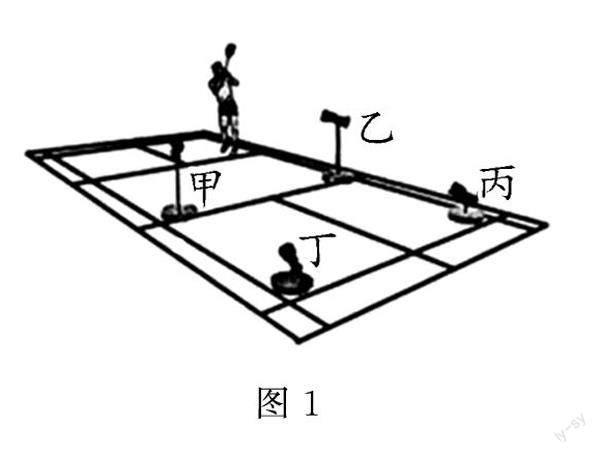
例1 林丹曾在一综艺节目中玩羽毛球定点击鼓游戏.如图1是林丹表演的场地，图中有甲和乙两个鼓，其高度相同.图中还有丙和丁两个鼓，其高度相同但相对较低，假设林丹每次所发的羽毛球的位置不变，且都做平抛运动，那么下面说法正确的有（）

（A）可以击中甲、乙两鼓的羽毛球的初速度关系为v甲=v乙.

（B）可以击中甲、乙两鼓的羽毛球的初速度关系为v甲>v乙.

（C）如果某次所发出的羽毛球能够击中甲鼓，则用相同的速度发出的羽毛球也可以击中丁鼓.

（D）能够击中四个鼓的羽毛球中击中丙鼓的羽毛球初速度最大.

分析 由于甲鼓和乙鼓的高度一样，则击中它们的羽毛球飞行时间相同.由于林丹到鼓的距离不同导致击中甲鼓的羽毛球飞行水平距离较大.由v=x/t得，击中甲鼓和乙鼓的两羽毛球的初速度关系为v甲>v乙，则（A）选项错误，（B）选项正确；从图中可知，林丹和甲鼓、丁鼓并不在一条直线上，因而使用相同的速度发球，不可能击中丁鼓，（C）选项错误；丁鼓和丙鼓的高度相同，从图中可以分析出，丁鼓到林丹的水平距离是最大的，因而击中丁鼓的羽毛球的初速度大于击中丙鼓的羽毛球的初速度，（D）选项错误.

点评 把该物理情境转化为平抛运动模型，利用竖直运动求时间，利用水平运动求初速度，结合具体情境，即可比较初速度关系.

2 利用平抛运动的对称性

由于碰撞导致运动本身具有对称性.结合对称性，运用平抛运动的相关规律可以实现对问题的求解[2].

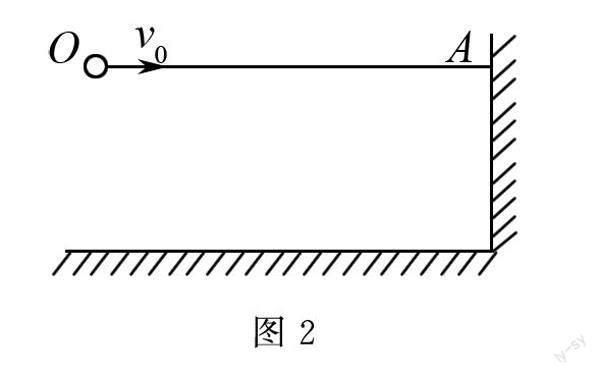
例2 如图2，小明将一个篮球（篮球可视为质点）以速度v0从水平面上方的O点水平抛出，篮球与水平面发生一次碰撞后，正好击中竖直墙壁上的A点，O点和A点的位置一样高.假设小球在碰撞过程中竖直分速度大小不变、方向正好反向，而水平分速度不变.现在仅改变初速度的大小，保证小球仍然能够击中A点，那么初速度的大小可能是（）

（A）2v0. （B）3v0. （C）v0/2. （D）v0/3.

分析 設竖直高度为h，小球以v0的速度平抛时与地面碰撞一次，反弹后与A点碰撞，在竖直方向先加速后减速，水平方向的速度保持不变.由对称性分析可知，这个过程的总时间是平抛运动时间的两倍，为t=22h/g.水平的位移则为OA=v0t=2v02h/g.假设平抛运动的初速度是v′0，小球与地面发生n次碰撞后反弹仍然与A点发生碰撞，那么它的运动时间是t′=n·22h/g，水平方向的位移不变，则有v′0=OA/，解得v′0=v0/n（n = 1，2，3……），故当n=2时v′0=v0/2；当n=3时v′0=v0/3，故（A）（B）错误，（C）（D）正确.

点评 本题是平抛运动的多解问题，结合对称性，挖掘多解条件，利用水平方向和竖直方向的等时性求解初速度的可能大小.

3 斜抛运动到最高点的逆过程为平抛运动

根据逆向思维，将斜抛运动到最高点可视作平抛运动，然后，利用匀变速直线运动的相关规律求解，是解决实际平抛运动的重要技巧[3].

例3 如图3，一名杂技演员正在表演飞刀，他从O点先后抛出三把飞刀，三把飞刀完全一样.一个木板竖直地放置在地面上，三把飞刀分别垂直地打在了木板上的M，N，P三个位置.假如O，M，N，P四个位置到地面的高度分别是h，4h，3h，2h.则下面选项正确的是（）

（A）三把飞刀打在M，N，P三点时的速度相同.

（B）三把飞刀飞行的时间比值是1∶ /2∶ /3.

（C）在三把飞刀抛出时，它们的竖直分速度比是3∶2∶1.

（D）如果三把飞刀抛出时的速度和水平方向的夹角分别是θ1，θ2，θ3，则θ1>θ2>θ3.

分析 可以逆向观察，将飞刀的斜抛运动当成平抛运动来处理.则飞刀击中三个位置时的速度看成反向平抛运动的初速度.竖直位移不一样，运动时间不一样，而水平位移一样，则初速度大小不一样.因此，选项（A）错误.采用逆向思维后，飞刀在竖直方向上做自由落体运动，飞行的时间分别为t1=6h/g，t2=4h/g，t3=2h/g，则飞行时间之比为3∶2∶1.因此选项（B）错误.三把飞刀在抛出时的竖直速度分量为反向平抛运动末速度的竖直分速度，根据vy=2gh，得竖直分速度比为3∶2∶1，因此选项（C）错误.飞刀抛出时的速度对应了反向平抛运动的末速度，与水平方向的夹角的正切值为tanθ=vy/vx=2gh/xg/2h=2h/x.可以得到，θ1>θ2>θ3，因此选项（D）正确.

点评 本题利用逆向思维，利用自由落体的比例法求解.在比较相关物理量时，写出解析式，看所求物理量随变量如何变化是解决该类问题的通用方法.

4 结语

平抛运动可以单独命题，也可和其他知识综合命题，掌握解决这类问题的方法尤为必要，复习中，学生应予以重视.

参考文献：

[1]李维兵.物理教材资源的融合与开发——以人教版“曲线运动”一节为例[J].教学与管理，2018（31）：44-46.

[2]林钱冰.高考试题中的物理模型分析与教学策略研究[D].福州：福建师范大学，2020.

[3]吴强.平抛运动及其应用[J].物理教学，2009，31（03）：59-61.