基于UWB辅助的多无人机惯导定位误差校正方法
马振华,张鹏飞,何 印,刘磊磊,郭伟峰
(1.中北大学 航空宇航学院,太原 030051;2.中北大学 智能武器研究院,太原 030051)
0 引言
无人机是利用无线电遥控设备和自备的程序控制装置操纵的不载人飞行器,一经研发出来就受到各领域的广泛关注。在民用领域使用无人机可以节省大量人力的同时还可以执行相对危险复杂的任务,不受环境限制。在军用领域使用无人机可以凭借其飞行高度低、体积小的特点从而难以被敌方雷达发现,让我方掌握战场的主动权,而且还可以减少我方士兵的伤亡。随着近几十年我国军工和民用领域技术的迅速发展,许多学者在多智能体控制、信息融合和无线通信等技术领域开展了大量的研究,使得无人机技术在军事和民用中的应用也日趋成熟[1]。与此同时,需要无人机执行任务的环境越来越复杂,如战场、搜索救援、海面漏油清理等空间广阔的任务环境,单一无人机由于覆盖面积小、负重量少等缺点,不能满足任务要求。受自然界生物集群的启发,多无人机又称为无人机集群出现在人们视野中。无人机集群在农业、军事、搜索救援、漏油清理、无人地带探索等方面应用广泛[2-4],多无人机联合执行任务的方式受到极大重视。相较于单架无人机,多无人机可以发挥数量优势,通过成员之间的协作,不仅可以扩大覆盖面积,更因为信息共享可以发挥“1+1>2”的执行任务效率,大大减少执行任务的时间,同时还可以增加信息感知范围,任务完成的可靠性得到提高[5-7]。
在多无人机编队执行任务过程中,作为无人机的眼睛,导航技术贯穿任务始终,高精度的位置导航信息是可靠完美执行任务的关键所在,但是多个无人机都搭载高精度导航设备涉及到成本问题,而且在卫星导航拒止的环境下定位变得异常艰难。惯性导航系统(inertial navigation system,INS)是目前应用普遍,不可缺少的一种隐蔽的自主导航系统[8],其无需任何外来信息,通过陀螺仪和加速度计测量飞行器自身角速度和加速度信息从而获得位置、速度以及姿态,具有短时精度高、更新率高、自主性强等特点,是编队飞行的各无人机成员的最佳导航方式。但是惯导最大的缺陷就是定位误差随时间而积累,需要利用其他导航定位信息不断对其校正。针对无人机集群的协同化编队飞行,若能利用无人机之间的相对距离信息来修正惯导误差,不仅能节省安装其他辅助导航系统的成本,而且定位精度高,鲁棒性也更强[9-10]。
目前国内外学者一般采用GPS接收机、视觉传感器等设备来校正惯导误差。文献[11]分析了捷联惯导系统的主要误差源对系统的影响及误差特性,通过卡尔曼滤波将GPS与捷联惯导系统组合,用GPS的导航信息对捷联惯导系统的误差进行了有效校正,这是目前常用的组合导航方法,但是在卫星导航拒止的环境下,卫星对无人机的定位信息丢失,惯导误差会迅速发散。文献[12]提出一种双伪卫星辅助的惯导误差校正新方法,在伪卫星数目只有两颗时,该方法仍可利用伪卫星的伪距测量序列将惯导的位置误差和接收机钟差估计出来,但是在探测不到伪卫星信号时同样面临方法失效的问题。文献[13]描述了一种基于视觉的相对导航和控制策略,使用视觉惯性系统检测未知和非合作的空间物体,用视觉导航设备获取载体间的相对视线矢量,校正相对惯导信息,但是视觉在室外易受环境变化和光线的影响,而且利用视觉往往会延时,不利于实时定位。文献[14]提出了利用地标的图像信息来校正惯导系统误差,通过光电平台摄取在飞行区域预设地理位置已知的地标图像信息和距离信息,对比对应的模板图像得出飞机位置信息,再结合惯导输出的位置信息,进而校正惯导误差。这种方法适用于已知区域,在未知的环境并不适用。文献[15]利用机载数据链的测距信息结合惯导信息建立机间相对定位模型,一定程度上减缓了惯导定位误差的发散速度,提高了定位精度。相较于其他传感器,本文所用的超宽带(ultra wide band,UWB)模块具有数据传输速度快、多径分辨能力和抗干扰性能强、易携带、测距准确且安全性高的特点[16-17],在多无人机惯导定位误差校正方面,测量的相对距离信息实时性和准确性都能得到保障,使得惯导误差校正效果更好。
本文给出一种运用UWB测距信息辅助的惯导误差校正方法,该方法突破以往的单一物体定位,利用UWB的测距信息实现多个无人机惯导定位误差的校正,来满足无人机编队在卫星拒止环境下的定位需求。文中首先给出UWB测距原理和惯导相对距离算法模型,其次给出惯导误差模型,并且设计出用UWB的测距信息校正惯导误差的扩展卡尔曼滤波器,最后通过仿真验证了方法的可行性。
1 无人机编队相对距离算法
计算不同位置的无人机之间的相对距离时,一般以无人机的机体坐标系为基准坐标系,如图1所示。无人机的机体坐标系是固定在无人机的遵循右手法则的直角坐标系,其原点位于无人机的质心,OY轴平行于机身轴线指向机头方向,OX轴垂直于对称面指向无人机右方,OZ轴在无人机对称面内,垂直于XOY平面指向无人机上方,构成右手坐标系。

图1 相对距离观测原理图

图2 双边双向测距原理图
无人机的相对距离是指某一架无人机在另一架无人机机体坐标系下距离坐标系原点的之间的距离,简单来说就是两个机体坐标系原点的距离,只不过需要其中某一个机体坐标系作为参考基准。相对距离可以将多无人机编队飞行时之间的距离变化直观地表现出来,这也是为什么在机体坐标系下测距的原因。无论是利用惯导解算出的位置信息还是UWB测得的距离信息都需统一转换到机体坐标系下进行相对距离的解算,这样才便于二者信息的融合。
1.1 UWB无人机间测距原理
UWB是一种无线载波通信技术,它不采用正弦载波,而是利用纳秒级的非正弦波窄脉冲传输数据,传输速率非常高。UWB测距原理是使用时间戳差值法计算电磁波飞行时间,从而计算距离。简单来说,无人机搭载的UWB模块主要是利用信号在两个异步收发机之间的飞行时间来测量无人机之间的距离,这种简单的单向双边测距如果两个设备时钟不同步会引入较大的测量误差,所以本文采用双边双向测距法[18-19],原理图如2所示。
图中Tprop是消息传播时间,Tround1和Tround2是从发出消息到接收到消息的时间间隔,Treply1和Treply2是从接受到消息到发出消息的延时时间,单边双向测距整个测距过程就是模块A在TX时刻向模块B发出消息,在经过Tprop时间后B模块接收到消息,然后B模块经过Treply的短暂延时后再向A发出消息,再经过Tprop的时间,A接收到消息。而双边双向测距是在单向双边测距的基础上再增加一次通讯,两次通讯的时间可以相互弥补因为时钟偏移而引入的误差。从而提高测距精度。利用双边双向测距法的信号传播时间计算公式为:
(1)
计算出电磁波传播在无人机之间的传播时间Tprop后,已知电磁波通讯的速度为光速,则无人机1和2之间的机体坐标系下的距离计算公式为:
(2)
式中,c是光速。
1.2 惯导相对距离解算模型
惯性导航系统利用陀螺和加速度计分别测量运载体的角运动信息和线运动信息,机载计算机根据这些测量信息解算出无人机的航向、姿态、速度及位置。无人机主要搭载的是惯性导航系统中的捷联式惯性导航系统,其原理如图3所示。

图3 捷联惯导原理图

图4 扩展卡尔曼滤波计算流程图
从图3可以看出,在使用捷联惯导时必须已知载体的初始速度、位置和姿态矩阵,结合捷联惯导陀螺仪和加速度计测得的信息进行速度、位置和姿态矩阵的更新计算。在计算姿态矩阵时,将陀螺仪测得的角速度减去根据导航坐标系和位置速度计算得到的角速度,得到的差值用来更新姿态矩阵[8]。在解算出姿态矩阵后,就便于将加速度计测得的机体坐标系下的比例值转换到导航坐标系中用于速度和位置的更新计算。此外,利用姿态矩阵和姿态角的关系,还可以计算得到姿态角。本节核心内容主要是给出捷联惯导的位置详细解算过程,从而建立基于惯导的无人机之间相对距离的解算模型。
设惯导的速度和位置的采样更新周期T为:
T=tm-tm-1
(3)
式中,tm和tm-1分别代表tm时刻和tm-1时刻。
选取东北天坐标系为惯性导航坐标系n,根据惯导的比力方程可得无人机的速度方程为:
(4)
解算出速度后无人机的纬度L、经度λ、高度h的微分方程为:
(5)

(6)
(7)
(8)
则有:
(9)
将式(9)在一个周期T积分可得:
(10)
即tm时刻运载体的位置为:
(11)
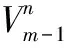
(12)

(13)
2 基于UWB测距辅助的惯导误差校正模型
UWB的测距速度快、精度非常高,能达到厘米级,利用UWB模块测量的无人机之间的距离可看作是真实距离。无人机各自搭载的惯导设备测得的位置信息相减之后转换到机体坐标系下同样能够获取无人机之间的距离。使用扩展卡尔曼滤波将UWB测得的真实距离和惯导信息融合构建惯导误差校正模型,使用真实距离来校正惯导误差。构建惯导误差模型之前需要分析惯导误差,从而确定滤波器的参数。
2.1 惯导误差模型
惯性导航的误差随着时间不断积累,在速度、位置、姿态三方面都会产生误差,不能长时间用于导航定位。为了建立准确的惯导误差校正模型,分析惯导在速度、位置以及姿态的误差影响源显得尤为关键。本文通过建立捷联惯导的误差模型[20],明确影响误差的各种变量,为建立惯导误差校正模型奠定基础。
2.1.1 姿态误差方程
惯导姿态误差方程为:
(14)
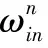
2.1.2 速度误差方程
根据式(4)可得惯导速度误差方程为:
(15)
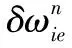
2.1.3 位置误差方程
选取地理坐标系为惯性导航坐标系,对式(5)的位置微分方程求偏差,考虑到式子中的RM和RN在短时间内变化很小,看作常值,可得在经度、纬度和高度误差方程:
(16)
式中,δL表示纬度误差,δλ表示经度误差,δh表示高度误差,记惯导在惯性导航坐标系下的速度分量为Vn=[VEVNVU]T,速度误差分量为δVn=[δVEδVNδVU]T。
2.2 惯导误差校正模型
2.2.1 状态方程
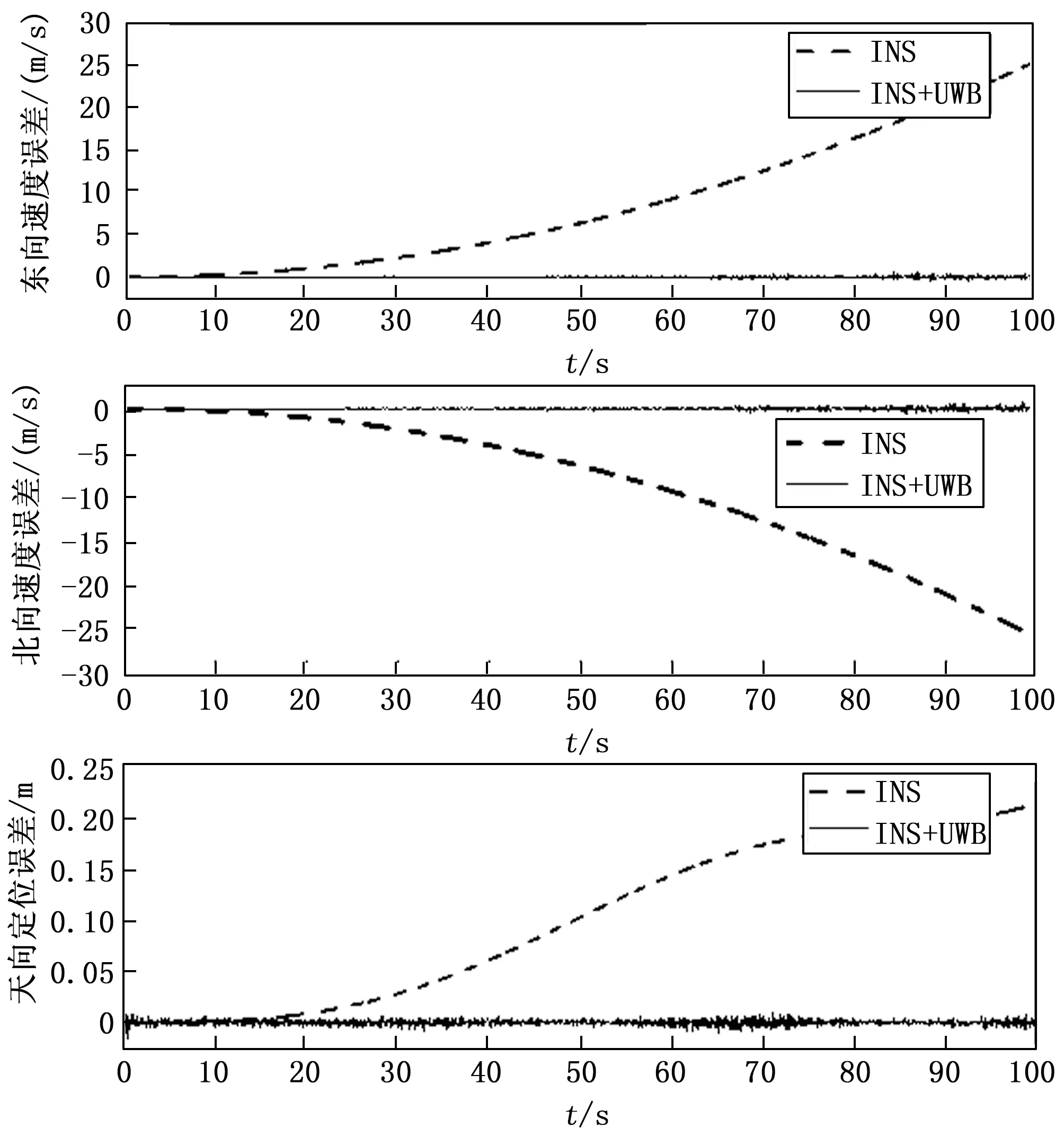
设共有k架无人机,以惯导误差作为状态量,则第i(0 (17) (18) wi(t)是零均值的白噪声序列,Gi(t)为系统的误差系数矩阵,Fi(t)为状态矩阵: (19) (20) 2.2.2 量测方程 以UWB的测距信息作为观测量,由于本文假定UWB在安装过程中经过标定,已经和无人机机体坐标系重合,因此无人机i获取的与无人机j的相对距离可表达为: (21) (22) 式中,Hi(t)是第i架无人机的量测矩阵,Vi是第i架无人机量测噪声序列,这里看作是零均值的白噪声序列。 2.2.3 扩展卡尔曼滤波模型 构建完状态方程(17)和量测方程(22)后利用扩展卡尔曼滤波进行更新计算,其中将状态方程和量测方程离散化得: Xk=Φk,k-1Xk-1+Γk-1Wk-1 (23) Zk=HKXk+Vk (24) 进一步可得扩展卡尔曼滤波公式为: (25) (26) (28) (29) (30) 式中,Φk,k-1为离散化的状态转移矩阵,R和Q为量测噪声和系统噪声的协方差矩阵,P为估计协方差矩阵。具体算法流程图如4所示。 设定两架无人机编队飞行,分别为无人机1和2,都搭载相同的捷联惯导系统、通信设备和UWB模块,无人机2伴随无人机1飞行,两架无人机除了起始位置不同,飞行轨迹完全相同,通过UWB测量无人机间的相对距离来相互校正惯导定位误差。仿真过程中考虑UWB测距噪声为高斯噪声。仿真参数如表1所示。 表1 仿真参数设置 通过对两架无人机编队飞行只依赖惯导定位和搭载UWB辅助惯导定位的两种不同情况进行仿真。无人机1和无人机2的100 s内纯惯导定位和UWB辅助惯导定位速度误差曲线走势图如图5和图6所示,并结合速度误差仿真数据给出了校正前后的速度均方根误差值如表2和表3所示。 表2 无人机1速度误差校正前后对比 表3 无人机2速度误差校正前后对比 图5 无人机1速度误差校正前后对比图 图6 无人机2速度误差校正前后对比图 从图5可以看出在卫星拒止环境下,无人机1只依赖惯导定位时,初始速度误差比较小,但随着定位时间的增加,速度误差也在不断地增加,在100 s时东向和北向速度误差达到0.5 m/s,在天向速度误差虽然在波动,但是误差同样有所增加,总的来说速度误差呈现发散的情况。而无人机1利用UWB测距辅助惯导定位时三个方向的速度误差都围绕0 m/s上下微小的波动,初始速度误差相较于纯惯导会大一些,这主要和滤波器参数设置有关,但这微小的误差在可接受范围之内,且随着定位时间的增加误差迅速收敛,而且结合表2可以直观地看出利用UWB辅助校正惯导速度误差的收敛情况与可行性。 从图6可以看出在拒止环境下,无人机2只依赖惯导定位面临着和无人机1同样的问题,东向和北向速度误差随着定位时间的增加越来越大,天向速度误差在0 s到70 s内先增加后减小,在70 s到100 s时速度误差又在不断增加,相较于UWB辅助惯导定位而言可认为其在发散。同时结合表三速度均方根误差值可证明利用UWB的测距信息可以有效抑制无人机惯导速度误差发散,提升定位中的速度计算精度。 无人机1和无人机2的100 s以内的纯惯导定位和UWB辅助惯导定位的三个方向的位置误差曲线走势如图7和图8所示,并结合仿真数据给出校正前后的波动峰值如表4和表5所示。 表4 无人机1位置误差校正前后波动峰值 表5 无人机2位置误差校正前后波动峰值 图7 无人机1位置误差校正前后对比图 图8 无人机2位置误差校正前后对比图 从图7可以看出无人机1只依赖惯导定位时在东向和北向初始10 s的误差比较小,但是在10 s之后定位误差开始发散,随着定位时间的增加误差也在不断增大。天向定位误差在15 s前比较小,但在15 s之后同样开始发散,只依赖惯导无法胜任无人机1的导航定位任务。反观UWB测距辅助惯导定位三个方向在100 s以内的定位误差都在0 m上下微小波动,结合表4来看,只依赖惯导定位时,东向和北向的波动峰值都超过了25 m,在天向达到了0.21 m,UWB辅助惯导定位的各方向位置误差则不超过1 m,校正结果显著,惯导的定位误差得到有效抑制。 从图8可以看出无人机2只依赖惯导定位时的各方向定位误差曲线走势与无人机1基本一致,这是因为在仿真时设置的二者搭载相同的惯导系统且轨迹相同,同样位置误差随着定位时间的增加在不断增加。通过UWB测量的无人机间的相对距离同样能够校正无人机2的惯导定位误差,误差曲线走势平稳,定位精度高。根据表5的峰值数据可以直观的看到校正前的东向和北向的定位误差在100 s的时间内超过了25 m,在天向波动峰值为0.21 m,校正后的各方向定位误差不超过1 m。 上述内容对仿真结果中速度和位置误差的校正前后曲线图以及表中数据进行了详细分析,可以说明本文利用UWB辅助惯导定位的方法对于校正惯导定位误差、提升惯导定位精度的可行性与有效性。 本文利用扩展卡尔曼滤波算法将UWB测量的无人机之间的相对距离信息和惯导信息融合,进而校正惯导的速度和位置误差。该方法主要存在以下几点优势: 1)UWB利用纳秒级的非正弦波窄脉冲传输数据,具有多径分辨能力强和抗干扰性能强的特点,采用双边双向测距消除了设备时钟不同步引入的测距误差,进一步提升了测距精度,经过标定和无人机机体坐标系重合后可以精确测量无人机机体坐标系下的相对距离,保证了相对距离数据来源的可靠性。 2)UWB仅用来测距,不参与定位,只需考虑测距过程的白噪声误差,使得扩展卡尔曼滤波融合算法实现相对简单,能够快速收敛,提升了算法的运行速度,保证了定位的实时性。 本文以在卫星导航拒止的环境下,多个无人机只依赖惯导无法长时间的编队飞行为背景,提出了一种利用UWB辅助的惯导定位误差校正方法,该方法融合了UWB测距信息和惯导信息,可利用无人机间相对距离校正参与测距的无人机惯导的速度和位置误差,抑制惯导误差的发散,结合仿真结果验证了方法的可行性与有效性,为多无人机编队在卫星拒止环境下的定位提供技术参考。但文章所用的扩展卡尔曼滤波算法会引入线性化误差,还可以针对这一点进行改进,进一步提升定位精度。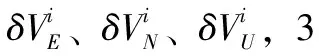
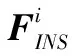
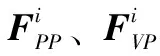

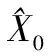
3 仿真分析
3.1 仿真初始条件
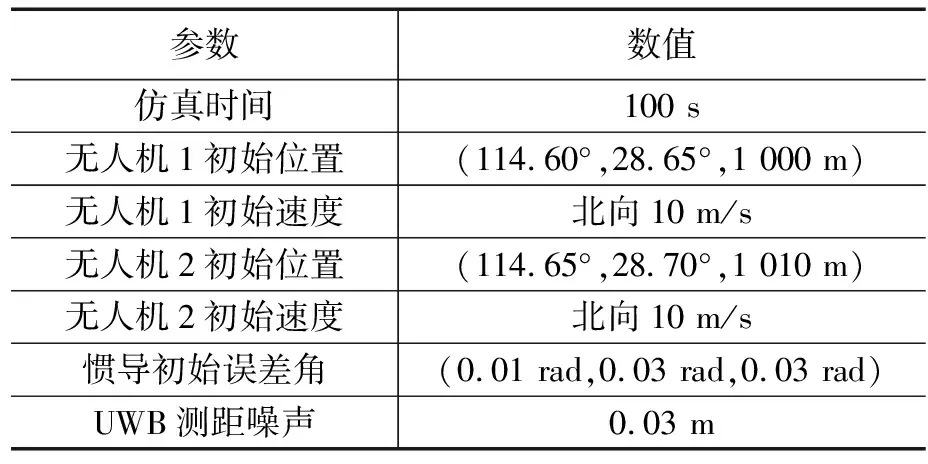
3.2 仿真结果及分析







4 结束语

