基于粒子群算法改进BP 神经网络PID 垃圾焚烧控制研究
罗佃斌,杨成慧,周德,马婉秋
(西北民族大学 电气工程学院,甘肃兰州,730030)
0 引言
自改革开放政策实施以来,尤其是进入二十一世纪,我国国民经济得到了迅猛发展,人民生活水平得到了显著提高,城乡规模不断得到扩大,城市人口不断增多膨胀,但生活垃圾的不断增多却成为目前世界上污染环境的一个重要原因之一。就目前生活垃圾处理情况来看,我国的生活垃圾废物主要处理手段可分为三种:填埋、焚烧和堆肥。垃圾焚烧发电是当今世界上垃圾无害化处理与资源合理利用最有效的方式[2]。
传统的PID 控制算法凭借其控制效果稳定性好、控制结构原理简单、易于实现、适用性和鲁棒性强等优点成为工业控制领域的主要技术之一,在工业领域中占据90%以上的地位,但传统的PID 控制算法在生活垃圾焚烧控制系统正常工作运行开始后参数是固定的,即参数不能在系统正常运行过程中自适应进行调整,故无法应对温度大范围变化、高复杂性这类被控对象。故提出了一种基于粒子群算法改进BP 神经网络PID 控制算法,将BP 神经网络与PID 算法结合,利用BP 神经网络自学习和自适应能力强等特点调整网络权值和阈值,并且BP 神经网络在一定条件下可以逼近任意非线性函数,然后再用PSO 算法对其进行改进,使其在全局训练得到最优值,防止其陷入局部最优值,进而对PID控制器的三个参数进行在线调整。
1 垃圾焚烧控制系统工艺流程
垃圾焚烧控制系统主要由垃圾进料系统、垃圾焚烧系统、蒸汽发电系统、烟气净化系统、除尘除渣系统6 大部分组成,其中整个控制系统的核心是垃圾焚烧系统。生活垃圾焚烧流程为:首先垃圾运输车将生活垃圾从城市的各地运到垃圾焚烧厂,生活垃圾在垃圾废池进行发酵烘干从而等待进一步处理。然后垃圾废物由垃圾机械吊抓斗抓取并送入垃圾料斗仓,再由推料机械手臂将垃圾推入焚烧炉内,依次完成发酵烘干、初次燃烧,充分燃烧、燃尽冷却的4 大过程,垃圾焚烧产生的有害烟气送入烟气净化系统处理,废渣送入除尘除渣系统处理,废水污水送入污水净化处理系统,废气废水经过处理后达到国家要求的标准再进行排放。
生活垃圾焚烧炉是一个具有强耦合性、大滞后性以及复杂、动态、不确定的非线性等特点的复杂控制系统,如果对垃圾焚烧时,焚烧炉温度过高,这样虽然提高了汽轮机发电效率,但是会使得钢坯表面造成耗损;如果焚烧的温度较低,则不仅影响发电的质量和稳定性,而且如果垃圾焚烧不充分,还有可能产生剧毒性气体二噁英[2],故需要对垃圾焚烧控制系统进行优化,保证垃圾焚烧温度的响应速度与稳定精度,最终实现垃圾的稳定燃烧。
2 BP 神经网络PID 控制
■2.1 传统PID 控制原理
传统PID 控制算法又称为比例-积分-微分控制,它是由比例(P)、积分(I)和微分(D)三个环节组成,再使得三个单独环节相互并联相加之后得到控制量,再和系统中的被控对象串联,从而对被控对象进行有效的控制,根据以上各环节相互连接所构成的这种控制器称为PID 控制器。和其他控制方法相比,传统的PID 控制算法凭借其结构原理简单、工作稳定可靠、适应性和鲁棒性强、使用方便等优点在工业控制领域中占据着独一无二的主导地位,目前PID 控制器在运动控制、航空航天、军事科技及其他过程控制中仍然占据90%以上。
PID 控制器的控制原理为:基于误差而生成消除误差的控制方法。控制系统通过比较反馈值和输入值的大小得到系统误差值,误差值经过控制器中比例项(P)、积分项(I)和微分项(D)的计算后,各项相加得到系统控制量,并作为对象输入量用于对被控对象进行调整。PID 控制结构图如图1 所示。
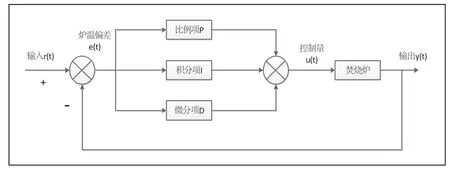
图1 PID 控制器结构图
PID 控制器的控制规律为:
式中:e(t)是垃圾焚烧炉炉温偏差,u(t)是控制量,Ti是积分时间常数,Td是微分时间常数,Kp是比例系数,Ki是积分系数,Kd是微分系数。
离散形式的增量式PID 控制规律:
其中:k是PID 控制器的采样序号,e(k)为第k次采样的偏差,e(k-1)为第k-1 次的采样偏差,u(k)为第k次采样的控制输出。
■2.2 BP 神经网络PID 控制器的设计
BP 神经网络算法是一种误差反向传播的前馈型神经网络模型,它是一种模拟人脑信息处理方法的大规模并行处理的自学习和自组织的非线性模拟系统,能够以任意精度逼近任意的连续非线性函数,对于不确定的复杂问题具有很强的自适应能力和自学习训练能力。
由于生活垃圾焚烧炉内各种垃圾焚烧温度变化的不稳定性与不确定性以及外界干扰的高度复杂性,严重影响了垃圾焚烧炉的温度控制精度、稳定性和响应速度。垃圾焚烧控制系统受较多参数的影响导致其抗外界干扰能力弱、稳定性比较差、控制精度低等,从而导致垃圾焚烧控制系统控制效果不理想,故传统PID 控制算法由于其结构简单、参数固定即不能在线实时调整等特点已不能满足其控制要求。近些年随着经济以及科技的快速发展,人工智能、机器学习以及深度学习逐渐受到人们的重视且得到了快速发展,模糊控制、神经网络、遗传算法、专家系统以及模拟退火等智能算法也因此应运而生,采用传统PID 控制算法与BP 神经网络相结合的方式,BP 神经网络可以根据其自学习与自适应能力在线实时整定PID 控制器的三个参数,从而在更大程度上发挥PID 控制的优点克服其缺点,从而使得控制系统具有更好的鲁棒自适应能力。BP 神经网络结合传统PID 控制系统结构图如图2 所示。
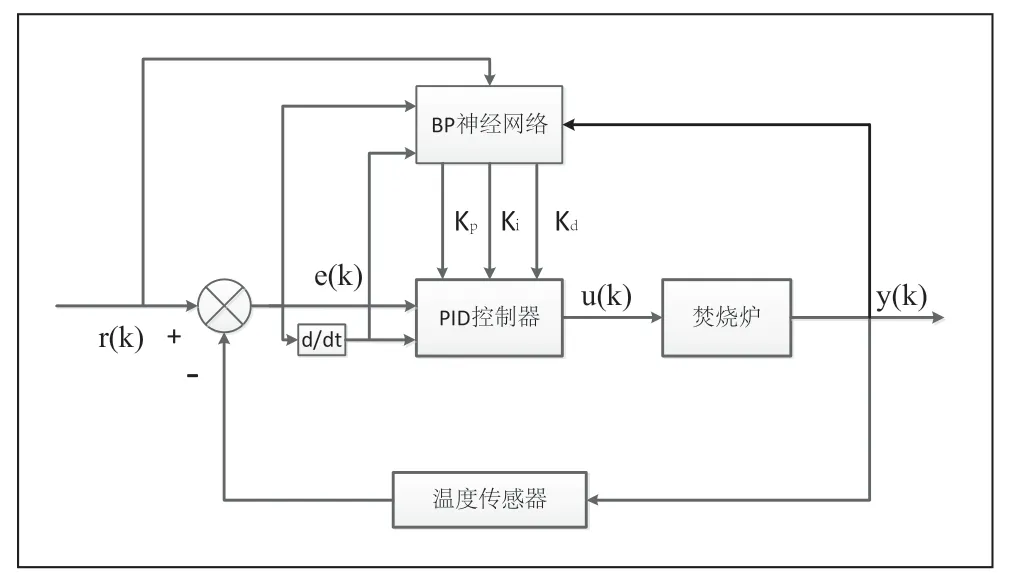
图2 BP 神经网络PID 控制系统结构图
BP 神经网络采用三层神经元结构来对PID 三个参数进行调整,三层分别为输入层、隐含层和输出层,各层神经元个数分别为:输入层神经元4 个、隐含层神经元5 个、输出层神经元3 个。BP 神经网络结构图如图3 所示。

图3 BP 神经网络结构图
(1)BP 神经网络正向传播过程:
输入层:设置输入层神经元个数为4 个,输入层神经元对应的4 个输入分别为焚烧控制系统温度期望目标值r(k)、控制系统温度实际输出值y(k)、系统温度偏差e(k)以及温度偏差变化率 ∆e(k),即输入层神经元的输入为:
输入层神经元的输出为:
隐含层:设置隐含层神经元个数为5 个,如果神经网络中隐含层神经元个数选取很少有可能产生的结果是网络根本无法进行学习训练或者网络学习训练性能非常差,从而影响整个神经网络的学习效果,神经元个数太多的结果虽然可能使神经网络系统误差减小,但这样会使网络训练时间延长,也会使学习训练陷入局部极小点而得不到全局最优点。隐含层神经元的激活函数选择S 型正切函数,。隐含层神经元的输入为:
隐含层神经元的输出为:
输出层:设置输出层神经元为3 个,输出层神经元的输出对应垃圾焚烧控制系统的三个参数Kp、Ki和Kd。由于PID 控制器的三个参数不能为负,故输出层神经元的激活函数选择非负的Sigmoid 函数[5],。输出层神经元的输入为:
输出层神经元的输出为:
PID 控制器三个参数为:
(2)BP 神经网络反向传播过程:
BP 神经网络期望输出与实际输出的偏差为:
取神经元输出的均方差为网络的目标函数:
利用负梯度下降法由输出层经过隐含层向输入层逐层调整各层神经元的权值,沿着误差E 的负梯度方向求解目标函数极小值时的权值。隐含层至输出层的连接权值修正量为:
其中:η 是学习速率,α为惯性系数。
输入层至隐含层的连接权值修正量为:
3 PSO 改进BP 神经网络PID 控制
■3.1 粒子群优化算法
粒子群优化算法(PSO)是一种进化计算技术,在1995 年由Eberhart 和Kennedy 提出[5],该算法是受到飞鸟群体觅食等活动的规律性启发,基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。
PSO 算法基本原理是在一个N 维搜索空间中有M 个没有质量和体积的粒子,每个粒子都具有一定的位置和速度矢量,粒子通过跟踪两个最优解pbest和gbest来更新粒子自己本身的速度和位置,然后通过多次迭代找到最终的最优解。粒子i 在N 维搜索空间中的位置表示为矢量:
第i 个粒子速度表示为矢量:
在每一维度下,粒子都有一个最大限制速度Vmax,在计算过程之中若某一维的速度超过最大限制速度Vmax则将做出合理化调整。
第i 个粒子局部最优解表示为:
粒子群全局最优解表示为:
第i 个粒子位置和速度更新公式:
其中:k为迭代次数;ω为惯性权重因子,ω越大全局寻优能力强,ω越小局部寻优能力强;c1和c2是加速度学习参数,通常取c1=c2=2;r1和r2是为了跳出局部最优的随机数,介于0 到1 之间;M 是粒子群体规模。
■3.2 PSO-BP-PID 控制器设计
BP神经网络在学习训练的过程中既有优点又存在缺点,其缺点是容易陷入局部极小点,而且有时也会因为初始权值与阈值随机选取不佳和学习速率大小选择不当而导致收敛速度过慢。粒子群优化算法(PSO)是一种全局寻优算法,其收敛速度很快,算法简单易于实现,将粒子群算法与BP神经网络结合,用粒子群优化算法来优化神经网络的连接权值和阈值,这样结合不仅可以发挥BP 神经网络的优势,又能克服BP 神经网络容易陷入局部极小值和学习训练速度过慢的缺陷[9],从而在一定意义上提高神经网络的收敛速度和学习训练能力。
将BP 神经网络中每一层的连接权值都作为粒子群中的一个粒子的某一维度,再将BP 神经网络的目标函数作为粒子群算法的适应度函数,然后通过多次迭代找到最优解。PSO 优化BP 神经网络步骤:(1)确定神经网络结构和PSO 算法参数。(2)将BP 神经网络的每一个连接权值作为粒子群的一个粒子一个粒子的某一维度并进行权值初始化。(3)根据适应度函数计算每个粒子的适应度。(4)对于每个粒子将其适应值与自己经过的最好位置pbest和粒子群最好位置gbest作比较,根据比较结果作出相应调整。(5)根据粒子群算法位置与速度更新公式调整速度和位置。(6)迭代终止条件一般选为最大迭代次数或最优位置满足预定最小适应阈值,不满足结束条件则转步骤(3)。
4 仿真及结论
由于焚烧炉是一个具有强耦合、大滞后以及非线性等特点的高度复杂控制系统,故垃圾焚烧炉其精确的数学模型很难建立。本文通过阅读大量文献,将垃圾焚烧炉被控对象的传递函数用二阶惯性环节加滞后延时环节来描述[9]。其传递函数[10]为:
其中:K是放大增益,τ是滞后时间,s是复变量。
设置单位阶跃信号为1,取c1=c2=2,ω=0.8,学习速率η=0.2,惯性系数α=0.2。传统PID 控制、BP 神经网络PID 控制以及基于粒子群算法改进的BP 神经网络PID控制系统仿真结果如图4 所示。

图4 仿真结果图
通过图4 仿真结果比较可知,基于粒子群优化算法改进的BP 神经网络PID 控制相比于传统PID 控制以及BP 神经网络PID 控制有更快的响应速度,上升时间更短,超调量更小,稳定性更高。通过比较可以看出PSO-BP-PID 控制相比于其他两种控制方式有明显更好的控制效果。

