一种长航时惯导定位误差评估的新方法

郭正东, 杨小康, 王小海, 戴建国

(1. 海军潜艇学院航海观通系, 山东 青岛 266199;2. 西北工业大学自动化学院, 西安 710072;3. 中国人民解放军92330部队, 山东 青岛 266102)

0 引言

近年来惯性导航技术突飞猛进,光学技术、量子技术、材料及精密加工技术等推动了惯性传感器技术,如量子陀螺、静电陀螺、光学陀螺、半球谐振陀螺等惯性仪器仪表的精度及性能得到大幅提升[1-3]。与此同时,信息技术从另一方面推动了导航系统应用技术的发展,采用平台旋转调制、虚拟平台监控、惯性元器件温度补偿等新方法后[4-6],一些原理性导航误差得到了有效抑制,使得导航定位解算的精度也不断提升。受两方面因素影响,惯性导航系统定位性能大幅提高、设备类型明显增多、更新速度加快,这给用户掌握装备性能造成一定困惑。特别是在军事应用领域中,长航时自主惯性导航系统的精度评估将对武器系统的作战性能产生重大的影响[7],比如潜艇自主定位精度的准确性和可用性,以及危险圆半径是潜艇海上避让危险物的重要参数[8-9];再比如在传递对准武器发射中的主惯导导航参数精度,以及主惯的姿态、速度和定位误差均会直接影响武器子惯导的相应参数,进而影响武器的命中精度[10]。

自主惯性导航系统的定位误差理论上是随时间而振荡发散的。在舰船等运载体低速航行的情况下,对高精度惯导而言,其纬度误差可以保持幅值有界的振荡,但经度误差总会不断累积变大,后者主要是由于受天向陀螺漂移的影响。虽然陀螺常值漂移可以通过采用双轴调制等技术手段减弱,但是随机漂移引起的定位误差是累积型的[11]。

为了从总体上降低长航时导航误差,部分厂商会根据低速运载体的运动特点,采取类似于内阻的技术[12-13]。但是这类技术破坏了惯导误差传播规律,使得惯导误差可能跟载体运动状态相关,具有较大的不确定性,片面影响了惯导使用者对惯导设备性能的认识,进而影响惯导实际应用效果。论文将提出一种新的惯导长航时定位误差评定方法,试图降低不确定误差的影响,对惯导系统是否符合惯导误差传播规律进行有效评估。

论文首先介绍了传统的导航定位误差评价方法,指出了将其应用于自主长航时导航的缺陷。接着,给出了一种基于惯导误差传播函数拟合的定位性能评价方法,对其进行仿真分析,并应用于实测数据对比分析,给出了合理的使用建议。

1 传统的位置偏差评价法

在航海学理论中,危险圆半径是海上避让危险物的唯一参数,据此采用位置偏差法作为惯性导航系统的关键评价指标,能够满足航海安全的保障需求[8-9]。从惯性导航系统技术的发展实际情况看,有关位置偏差的评价方法和评价形式也在不断发生变化,先后出现了圆概率误差(circular error probable,CEP)、均方根误差(mean square error,MSE)和最大值误差(MAX)等3种不同的评价方法[14-15]。每一次评价方法的调整和改进,都能推动惯性导航系统的技术进步。

下面以多次舰载导航实测实验结果中比较典型的一组测试数据对位置偏差法进行具体分析。

图1给出了5套某新型惯性导航系统舰载长航时自主导航位置误差的测试结果,并根据位置偏差法中的最大值评价方式,按照性能优劣判定结果,自上而下进行排序,最大误差不断增大。图1中,横坐标为时间,单位是天,取值范围[0,30];纵坐标是位置偏差,数值进行了归一化处理,无单位,但不同惯导之间可作相对大小比较。其中,前4幅小图取值范围[0,5];而第5幅小图取值范围[0,20],其精度稍差些。

图1 5套新型惯导位置偏差比较Fig.1 Comparison of position deviation of five new inertial navigation systems

从图1可以看出,5套惯导系统的定位误差随时间不断变化,且误差总体上都有较明显的周期性振荡和累积性等特点。按照最大值位置误差评价法,能将这5套惯导在某一时段内定位误差的极值准确表达出来。因此,当用户将其与危险圆半径进行关联后,采取该评价方法得出的性能指标可用于保障水下航行器的航行安全。此外,若采用一点校、两点校等校正手段[12-13],当水下航行器某次浮起使用外界定位时,对于该时刻获取的位置偏差观测结果,有些惯导(如1号惯导)难以反映出其定位规律,致使用户难以根据定位误差规律实现精确校准。

随着导航信息融合技术的快速发展,不少研究者开始在惯导装备技术层面采取误差补偿措施,对系统输出的导航结果进行优化。但是,若因某些信息技术的不当引入,继续采用位置偏差法对惯性导航系统进行评价时,评价结果除了符合惯性导航系统评价本身的要求外,不能科学反映出其内核技术性能有无实质性提升。

通过对图1中前2幅小图进行的比较可看出,1号惯导在第5 d时,位置误差已达最大值,整个30天航程中误差随时间累积的规律不是非常明显;2号惯导在导航后期位置误差才达到极值,且误差随时间累积的趋势非常明显。3号惯导精度中等,4号惯导舒拉振荡误差尤为明显,而5号惯导精度性能较差。下面主要针对1号和2号惯导作对比分析。1号惯导和2号惯导的位置误差在后期都有地球周期性振荡误差,从其振幅上看,1号惯导明显大于2号惯导。因存在以上两处矛盾,大部分行业专家开始倾向于2号惯导定位性能优于1号惯导的评估结论,并敏锐地认识到,仅采取位置偏差法,难以科学评价惯性导航系统的长航时定位性能,缺少对系统是否符合惯导误差传播规律的评价。

2 新的基于误差函数拟合的评价法

从惯性导航原理上看,惯导系统基于陀螺仪输出角速度和加速度计输出比力的积分不断递推得出姿态、速度和位置信息。由于在惯导解算过程中,惯导系统导航误差主要来自陀螺仪和加速度计的器件误差以及导航结果的初始误差,并按照惯导误差微分方程随时间变化,所以惯导系统误差会表现出很强的规律。

重新将前述1号和2号惯导系统的东向位置误差随时间变化图绘制出来,如图2所示。从图2中可以看出,1号惯导系统在前半段0～15 d的位置误差规律明显具有幅值较大的随机性,误差传播过程不太符合惯导误差方程表示的误差传递规律。而2号惯导系统在0～15 d中的位置误差规律,有更明显的周期性,并且误差随时间增加而缓慢增长。结合图1位置误差的变化情况来看,2号惯导系统的误差特性基本符合惯导原理解算过程导航误差变化,而从1号惯导系统的误差变化曲线中难以看出惯导系统误差变化的特点。从水下航行器运载系统保障和组合导航应用潜力两方面对比分析两惯导系统时,2号惯导系统表现更好,其误差特性更加符合惯导规律,误差变化更接近惯导系统误差模型。

图2 东向位置误差比较Fig.2 Comparison of eastwards position errors

为了能够弥补位置偏差法的不足,并准确且完整地分析惯导系统长航时定位性能,必须从惯导系统误差传播规律角度设计一种合适的评价方法。

通常高精度惯导系统的误差会比较严格地按照理论误差方程进行传播,对实际系统的误差进行长时间观测,其统计结果必然符合惯导误差方程的规律,根据惯导误差方程得到误差随时间变化的函数,然后进行曲线拟合,就可以找到实际惯导系统误差规律。拟合误差越小则说明惯导误差特性越明显,更有利于实际使用的优化和维护,而拟合误差越大则表明系统可能并不是进行纯惯导解算或者惯导稳定性较差,难以进行实际应用、误差预测评估和校正。

首先,给出惯导系统误差方程,姿态、速度和位置误差微分方程分别为

(1)

其中,各符号含义可参见文献[11]。根据误差方程可以推算出惯导系统误差变化规律,如果惯导系统利用惯性传感器数据进行惯导解算,其结果也必然符合误差规律,通过判断误差是否在分析的误差范围内,就可以判断出系统特性是否符合惯导系统内在特性。

长航时导航过程中,位置误差出现明显的周期项,包含舒拉振荡、傅科振荡和地球振荡。如果惯导系统进行纯惯导解算,其位置误差必然包含这三个周期项,即可用包含此周期项的函数对惯导位置误差数据进行曲线拟合。若惯导解算结果符合纯惯导解算规律,则拟合误差应当较小,若惯导解算结果不符合纯惯导解算规律,则拟合误差可能会较大。论文根据拟合误差定义的“惯导系统惯导误差规律契合度”,可用于惯导系统的定位性能评价。

根据捷联惯导误差方程式(1),定义用于拟合北向位置误差的简化模型如下

δp(t)=k1cos(ωiet)+k2+k3t+
k4cos(ωietsinL)cos(ωst)

(2)

式中,k1,k2,k3和k4为模型参数,L为纬度,ωie为地球自转角速度,ωs为傅科振荡角频率。如果以位置误差估计偏差的方差最小准则使用最小二乘算法可以完成式(2)的函数拟合,那么函数拟合的误差可以反映出惯导系统和纯惯导解算规律的契合程度,进而实现相同测试条件下,比较不同惯导系统输出误差与理论误差传播规律的契合度。

虽然式(2)中的模型是对于捷联惯导系统的近似描述,但是已经可以实现惯导位置误差拟合,并用于分析惯导系统输出和导航误差规律的契合程度。进一步增加模型参数、优化模型准确度等改进措施不但不能改善分析误差契合度和评估惯导系统的效果,而且会影响实测导航数据的拟合效果。

定义tk时刻实际惯导位置误差与拟合位置误差之间的偏差量为

(3)

L=∑l(tk)

(4)

最后,定义惯导系统的惯导误差契合度如下

(5)

式(5)中,T为导航解算时长。

惯导误差契合度λ可以用来表示惯导解算误差与惯导误差模型的契合程度:如果λ越小,则表示惯导解算结果越符合惯导误差模型,惯导系统特性越明显,越有利于惯导运载系统的保障和组合导航的应用;反之,如果λ越大,则结论相反。后文将通过仿真和实测数据分析对该结论进行验证。

3 仿真与试验数据验证分析

3.1 仿真验证分析

为了验证基于误差函数拟合的评价方法,先进行24 h的惯导解算仿真,得到导航误差数据。仿真中的惯导误差参数如表1所列。将北向位置误差的前一半数据加入随机游走误差,使该一半数据不符合惯导误差规律。两组位置误差数据如图3所示,第1组(sim.1)为完整的惯导北向位置误差,第2组(sim.2)为修改过的北向位置误差数据,两组数据均经过归一化处理,无单位。

表1 仿真惯导参数表

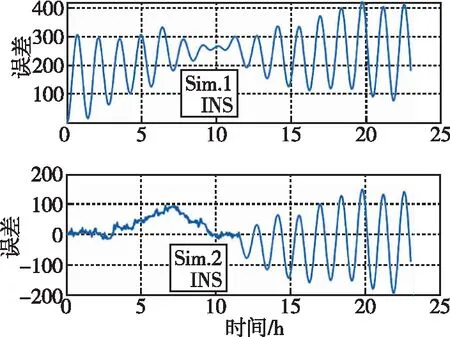
图3 两组惯导位置误差仿真Fig.3 Simulation of two sets of INS position errors

用第2章中提出的评价方法处理图3的两组位置误差数据,得到的位置误差与位置误差拟合函数的对比如图4和图5所示。两组位置误差数据的惯导误差规律契合度计算结果参见表2。

图4 第1组误差数据拟合结果Fig.4 Fitting result of group 1 error data

从图4中可以看出,北向位置误差拟合结果与实际位置误差曲线非常接近,两者拥有相同的周期性误差,说明实际的北向位置误差变化符合惯导系统北向位置误差规律。从图5中的结果可以看出位置误差数据的后半段符合惯导误差规律,这段数据与拟合得到位置误差变化曲线有相同的周期性,但是前半段数据形态与拟合的位置误差函数基本不同。

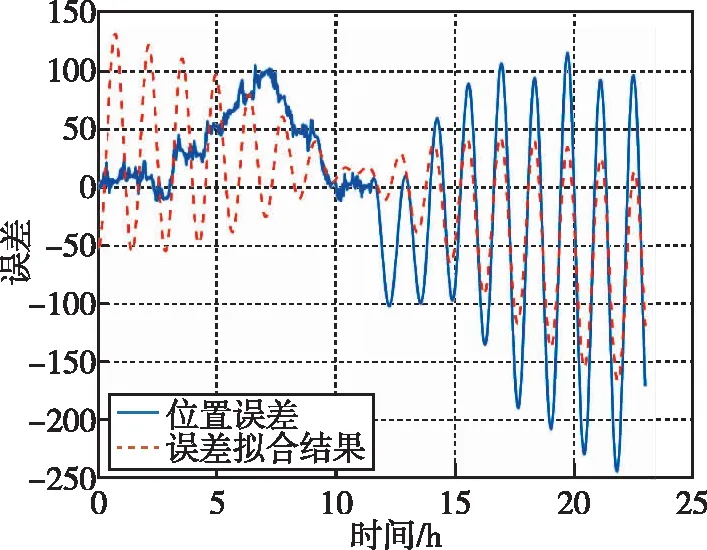
图5 第2组误差数据拟合结果Fig.5 Fitting result of group 2 error data

表2中给出了两组数据的惯导误差规律契合度参数,第1组数据的参数λ小于第2组数据。这主要是由于第2组数据前半段与惯导位置误差规律不符合,实际数据与拟合函数的结果相差过大造成的。根据参数λ的大小,可以判定第1组惯导系统的结果更加接近惯导系统的误差模型。

表2 两组误差的惯导误差规律契合度

根据仿真结果可以判定第1组惯导的惯导特性更加明显,采用第1组惯导有利于惯导运载系统保障和组合导航应用,该结论与仿真条件一致。因此使用惯导误差规律契合度进行惯导系统性能判定是可行的。

3.2 试验数据分析

为了进一步检验文中提出的基于契合度的惯导系统性能判定方法,使用图1中的1～5号惯导系统实测位置误差数据进行分析。

将1～5号惯导数据代入式(2)表示的误差模型,得到拟合后的惯导误差函数,比较拟合函数与实际误差数据的差异,根据惯导误差规律契合度的定义计算参数λ,量化计算实际数据与误差拟合函数之间的差异。比较两组数据的参数λ的大小,并以此对两套惯导系统进行性能评估对比。

1～5号惯导系统的北向位置误差与北向位置误差拟合函数的对比如图6所示;系统位置误差数据的惯导误差规律契合度计算结果如表3所列。

图6 1～5号惯导系统的误差数据拟合结果Fig.6 Fitting result of error data for INS No.1～5

从图6的结果对比可以看出:

1) 1号惯导系统的北向位置误差前半段数据中没有明显的地球周期误差项,与惯导误差模型相差较大;2) 2号惯导系统北向位置误差呈现出周期性,误差变化趋势与惯导北向位置误差拟合函数相近;3) 3～5号惯导的结果说明提出的评估方法可以适用于不同的惯导系统,各个惯导系统的位置误差变化虽然不同,但是其规律在试验全过程中保持一致,且可以用式(2)中的函数完成拟合;4) 受陀螺噪声影响,实际系统的误差规律更加复杂,虽然实际数据与位置误差拟合结果有偏差,但是实际误差数据在误差变化的周期性上与拟合结果十分接近。

表3 五套惯导系统的惯导误差规律契合度

根据表3中五套惯导系统的惯导误差规律契合度计算结果可以得出如下评估结论:2～5号惯导系统的位置误差变化特征更加符合惯导误差模型中位置误差函数的结果,其位置误差数与位置误差函数拟合结果的偏差更小,因此第2～5号惯导系统相比1号惯导系统更有利于精确校准和优化维护,进而可能达到更优的组合导航应用性能。这与前述的基于传统的最大值评价方法结论正好相反。需注意的是,由于误差契合度反映的是惯导系统符合惯导误差传播规律的程度,一个定位误差较大的系统可能因随机误差、动态误差相对不明显,反而取得较小的契合度数值。因此,误差契合度更适用于相同条件下定位精度相近的惯导系统之间的横向比对,长航时惯导系统的全面评价也有赖于位置偏差法和误差契合度的综合运用。

4 结论

本文基于舰载惯导位置实测数据,开展了惯性导航系统定位误差评价方法研究,提出了基于误差函数拟合的惯性导航系统评价方法,给出了契合度量化指标的定义。试验数据检验结果表明,本文提出的评价方法更适合长航时惯导应用,也更符合惯性导航系统的内禀特征。

在惯性导航系统中采用综合导航系统技术,虽一定程度上提高了惯导设备在位置偏差方面的性能指标,但因其误差补偿技术成熟度不够,还不能满足惯导长航时自主导航需要。为了消除此类设备对水下航行器远航工作的影响,建议从两方面着手:一是在摸索惯导长航时定位性能时,综合使用位置偏差法和本文基于误差函数拟合的评价方法,通过比较惯导误差规律契合度,分析惯导性能;二是对新型惯导装备做出技术限定,将信息应用技术严格限定在综合导航系统技术层面。