基于矢量化检测联邦滤波的INS/BDS/地磁组合导航容错方法

邵宇强

(哈尔滨理工大学测控技术与通信工程学院, 哈尔滨 150080)

0 引言

随着科技的不断发展和进步,人类对于迈入深空、挺进深海、探索地球各个角落的热情日益高涨。导航是人类进行各种探索活动与科学研究的重要基础,目前对于高精度、高可靠导航手段[1]的需求与日俱增。以全球定位系统(global positioning system, GPS)、北斗卫星导航系统(Beidou naviga-tion satellite system, BDS)为代表的全球卫星导航系统是一种重要的导航手段,但卫星信号极易受到遮挡与干扰,难以在复杂环境下提供可靠的导航信息[2-3]。而其他常用的导航系统,例如惯性导航系统(inertial navigation system, INS)等也存在着各自的局限性[4],单独运行时无法提供连续精确的导航信息[5]。单一的导航方式已经难以满足日益增长的需求,一般采用多种导航手段相融合的方式,取长补短,进而提升导航系统的整体性能[6]。联邦卡尔曼滤波[7]是实现多种导航信息融合的主要方式[8],是一种分散化的多传感器数据融合方法[9],能够消除不同导航信息之间的相关性,并保证信息守恒,因此具有良好的容错性、精确性与高效性,是一种理想的容错信息融合算法。

保证基于联邦卡尔曼滤波的组合导航系统的性能的关键问题之一,是对各导航信息源进行有效的故障诊断,该问题已成为国内外相关领域专家和学者的重点研究方向,并在理论层面已经有了很多成果。在众多故障诊断方法中,χ2检验法[10]是应用最为广泛的故障诊断方法(包含状态χ2检验法和残差χ2检验法)。在进行组合导航系统故障检测时,一般将故障子系统当作一个整体来分析,并假设所有观测量具有相同的估计精度和收敛速度,按照统一的权重来分配信息[11],可称谓“基于系统层次的故障检测方法”。但是,在实际情况中,故障子系统里通常仍有部分观测量没有出现异常,这样就会造成对导航子系统信息利用不充分。为解决该问题,何广军等[12]提出了一种基于矢量信息分配的容错联邦滤波算法,能对每个状态变量单独进行故障判断和信息调整。吕建新等[13]提出了一种基于观测残差的自适应联邦卡尔曼滤波导航方法。当载体受到异常干扰或动力学模型有较大误差时,该方法能够根据观测残差自动调整信息分配权重,减小导航误差。不过,该方法只能影响子滤波器的状态估计质量,不会对主滤波器的状态估计质量产生影响。许丽佳等[14]提出了一种基于模糊推理系统和卡尔曼滤波的方法,用于克服联合卡尔曼滤波法的缺点。该方法能在线调整噪声统计特性,实现子滤波器和主滤波器的自适应融合。此外,他们还提出了一种新颖的信息融合算法,根据模糊推理系统给出的各状态估计量的信任权重,动态地进行加权融合,从而提高了融合精度。蒋锐等[15]在联邦卡尔曼子滤波器和主滤波器之间加入故障检测,自适应调整故障子滤波器的滤波增益矩阵。该方法可以有效检测系统故障并对其进行实时处理,提高系统的可靠性。

然而,上述传统方法均是对整个系统采取相同的检测机制,没有针对不同导航方式的特点矢量化地检测故障是否发生。对于导航信息丰富的系统而言,浪费了本可以使用的信息,而对于需要快速检测的系统,则增加了计算量。因此,本文采用INS/BDS/地磁导航的多源组合导航模型,设计了一种基于矢量化检测联邦滤波的INS/BDS/地磁组合导航容错方法。通过构建面向不同导航信息的故障检测函数,能够实现更加准确的矢量化信息分配,从而提高导航精度和容错性能。

1 INS/BDS/地磁组合导航模型

本文选择“东-北-天”导航坐标系作为参考坐标系。在该坐标系下,系统的状态变量包括位置误差、速度误差、姿态角误差以及陀螺仪和加速度计的随机常值漂移。

1.1 组合导航系统状态方程

X=[δE,δN,δh,δve,δvn,δvu,φE,

(1)

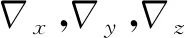
Xi(k)=Fi(k|k-1)Xi(k-1)+
Gi(k|k-1)Wi(k-1)

(2)

其中,Fi为系统矩阵,Xi为状态变量,Gi为系统噪声矩阵,下标i表示第i个子系统。系统噪声为

(3)

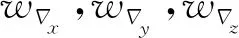
1.2 组合导航系统量测方程

针对INS、BDS和地磁导航3种导航方式的特点,以惯性导航作为基础导航方式,分别构造INS/BDS组合导航为子系统1,INS/地磁组合导航为子系统2,各子系统的量测方程如下。

子系统1:对INS与BDS的位置信息和速度信息分别做差构建观测量。

(4)

其中:RM,RN分别为地球子午面及卯酉面主曲率半径;NBe,NBn,NBu和vBe,vBn,vBu分别为北斗卫星导航沿东、北、天方向的位置误差和速度误差。

子系统2: 观测量选取为INS与地磁罗盘的姿态角误差。

Z2(k)=HaX2(k)+Va(k)

(5)

其中,量测矩阵Ha=[03×6,I3×3,03×6],Va(k)=[VMγ,VMθ,VMΦ]T为地磁罗盘量测噪声。

2 矢量化检测容错联邦滤波器设计

在本文提出的INS/BDS/地磁组合导航系统中,根据各子系统的特点,分别使用不同的故障检测方式。子系统1中,BDS易受环境影响从而产生误差,但其所能提供的导航信息较为丰富,若采用传统的故障检测方法,进行系统层面的故障诊断和隔离,会丢失正常的观测量信息,降低子系统1的信息利用率。因此,本文对子系统1的各状态变量分别进行故障诊断,只隔离其故障信息,对无故障的信息加以保留和利用,从而增加信息利用率。子系统2中,地磁罗盘通过测量地磁场提供姿态角信息[16],当存在磁场干扰或其他因素使得地磁场的测量存在故障时,信息不再可靠,需要快速检测隔离,且由于子系统2信息量相对较少,对其使用系统层面的故障诊断。

2.1 面向不同导航信息的故障检测方法

在卡尔曼滤波中,当故障发生时,其产生的残差会偏离零均值的高斯白噪声。因此,检测系统中的故障有赖于对残差的分析。故障检测通常采用基于残差的χ2检测法,构建一个故障检测函数,该函数可以捕捉到残差的统计特性,然后使用该函数来确定是否发生了故障。这种方法能够有效地检测出系统中的故障,并采取纠正措施以保持数据的完整性。基于χ2检测法,本文构建了针对不同类型导航信息的故障检测函数。

子系统1的矢量形式的故障检测函数为

(6)

(7)

其中,r1表示子系统1在k时刻的残差值,Λ1为m阶方阵,表示为

(8)

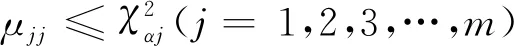
子系统2的系统层面的故障检测函数为

(9)

(10)

(11)

其中,r2表示子系统2在k时刻的残差值,V2(k)表示其方差。Λ2(k)～χ2(n),n为量测Z2(k)的维数。当Λ2(k)≤TD,判定为子系统2无故障;当Λ2(k)>TD,判定为子系统2存在故障。TD为预先设置的故障检测门限。

2.2 存在故障时的信息分配方法

信息分配系数的设置关系到联邦滤波器的性能。信息分配方案的不同会导致状态估计的精度和系统的鲁棒性的不同,两者往往难以兼顾[17]。对于各子系统,过大的系数会使全局融合精度下降;过小的系数虽然能提升全局估计精度,但也会致使系统稳定性更容易受故障量测信息干扰。因此,在联邦滤波器设计时,要同时考虑状态估计精度和系统鲁棒性,做好平衡。本文提出的方法通过动态地调整状态估计方差、系统噪声方差和量测噪声方差,可同时提高系统的精度和鲁棒性。

设子系统i的量测噪声系数为

Bi=diag(bi,1,bi,2,…,bi,j)

(12)

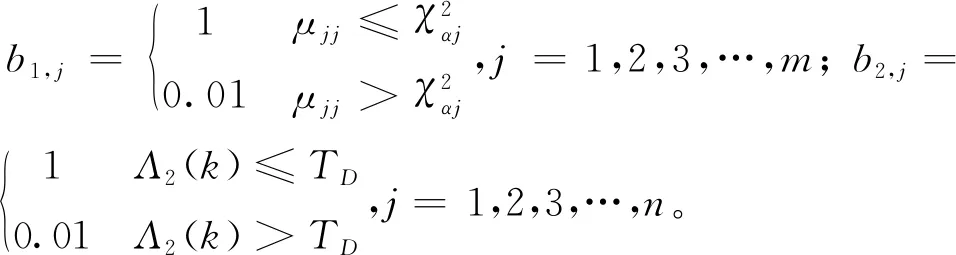
子系统1和2的观测量维数分别为m和n。对于出现故障的观测量,令其量测噪声系数为0.01;而无故障观测量的量测噪声应保持不变,其量测噪声系数设置为1。以此规则构造一个新的量测噪声系数矩阵Bi,从而实现对量测噪声方差阵的动态调整。具体如下

(13)

系统的估计精度可以由当前的误差估计方差体现,对第i个子系统的协方差阵Pi进行特征值分解,得到信息分配系数Gi[18]。

(14)

Li=diag(λi,1,λi,2,…,λi,n)

(15)

Αi=diag(αi,1,αi,2,…,αi,n)

(16)

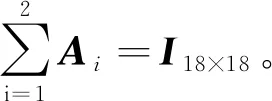
(17)

估计的准确性可以通过状态估计的方差来衡量。状态估计的方差越大,说明精度越低,因此,相应的分配系数应该越小。此外,还要确保每个子系统的状态协方差矩阵保持对称性,信息分配方式为

(18)

(19)

其中,Pg,Qg分别为主滤波器全局信息融合后的协方差矩阵和系统噪声矩阵;Pi,Qi分别为子系统i信息重置后的协方差阵和系统噪声矩阵。

2.3 容错联邦滤波算法

为减小主滤波器出现故障时反馈信息对子滤波器的不利影响,本文采用了如下的应对方法。首先,子滤波器独立完成其测量更新和时间更新,然后将所得信息输入主滤波器完成融合。融合后的信息按照设计的信息分配方法在各子滤波器之间进行分配,各子滤波器根据分配的信息再进行新的时间更新和测量更新。这种方法有效地解决了主滤波器故障对子滤波器信息的污染问题,同时保证了滤波过程的连续性和鲁棒性[19]。

根据上文提及的量测噪声系数Bi及信息分配系数矩阵Gi,设计容错联邦滤波算法:

(1)子滤波器时间更新

Xi[(k+1)/k]=Fi[(k+1)/k]Xi(k)

(20)

(21)

(2)故障诊断

建立故障检测函数Λi,对观测量进行故障诊断,得到量测噪声系数Bi和量测噪声矩阵Ri,减少对故障观测量信息的利用。

(22)

(3)子滤波器量测更新

即

{Hi(k+1)Pi[(k+1)/k]·

(23)

Xi(k+1)=Xi[(k+1)/k]+Ki(k+1)·{Zi(k+1)

-Hi(k+1)Xi[(k+1)/k]}

(24)

Pi(k+1)=[I-Ki(k+1)Hi(k+1)]·Pi[(k+

1)/k][I-Ki(k+1)Hi(k+1)]T+

Ki(k+1)Ri(k+1)[Ki(k+1)]T

(25)

(4)构建信息分配矢量系数Gi

(26)

(5)主滤波器信息融合

当子系统1中的部分信息失效时,采用如下的融合方式

(27)

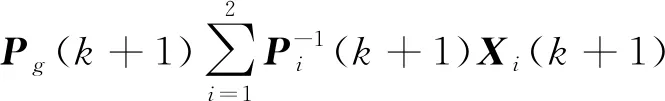
(28)

当子系统2失效时,对其整体隔离,因此系统误差状态的整体估计为

Xg(k+1)=X1(k+1)

(29)

此时,子系统2的输出估计值为

Z2(k+1)=H2Xg(k+1)

(30)

(6)子滤波器信息分配

(31)

(32)

Xi(k+1)=Xg(k+1)

(33)

由以上公式可得容错联邦滤波器结构如图1 所示。

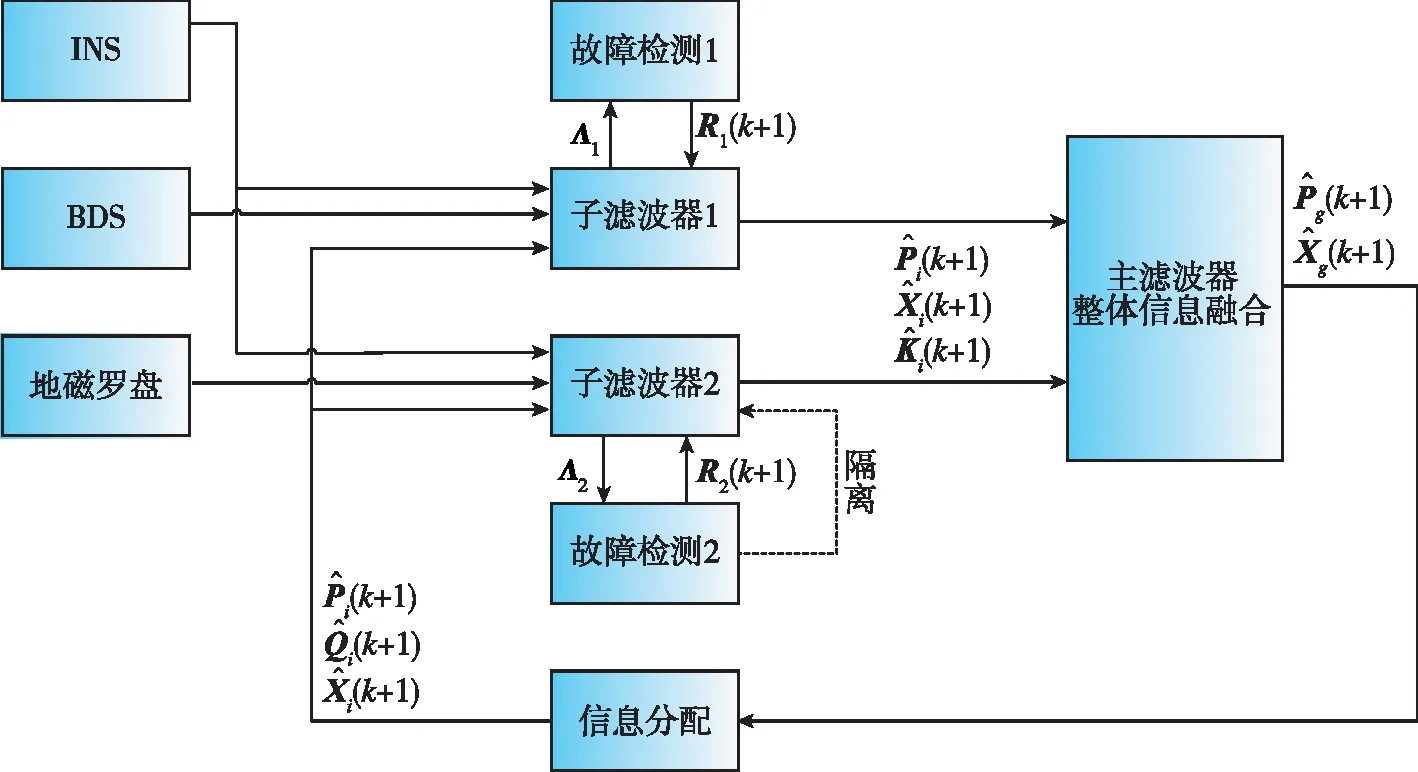
图1 联邦滤波器结构图Fig.1 Structure of the federated filter

子系统2中,由于地磁罗盘仅能提供姿态角信息,对于速度和位置状态的影响随时间累积较快,因此当其发生故障时,将其快速隔离有利于提高系统的整体精度。子系统2的故障检测函数Λ2相比于子系统1的Λ1,计算量减小,故障检测更快,从而能更快速地隔离故障。

当系统出现故障时,通过噪声系数放大故障观测量的测量噪声Ri,从而使协方差Pi变大,故障子系统在信息融合中的权重减小,进而减少了对它的信息利用。通过调节噪声系数bi,j来处理故障观测量,如果噪声系数较小,状态估计的精度就会降低,全局融合中对故障状态变量的使用减少;如果噪声系数较大,状态估计的精度就会提高,对故障子系统错误观测量使用减少,同时正确观测量的使用率增加。

3 仿真实验与分析

通过仿真实验对本文提出方法的有效性进行验证。采用INS/BDS/地磁罗盘组合导航系统,其中,INS/BDS组成子系统1;INS/地磁罗盘组成子系统2。模拟匀速直线运动,航向角为45°,真实速度为:东向速度vE=10 m/s,北向速度vN=10 m/s,天向速度vU=1 m/s。滤波周期为1 s,仿真时间为1 000 s。假设陀螺随机常值漂移为0.1 (°)/h,加速度计随机常值漂移为10-4g,BDS位置误差为10 m,速度误差为0.5 m/s,电子罗盘的航向角精度为0.5°,俯仰角、横滚角精度为0.1°。

3.1 无故障发生

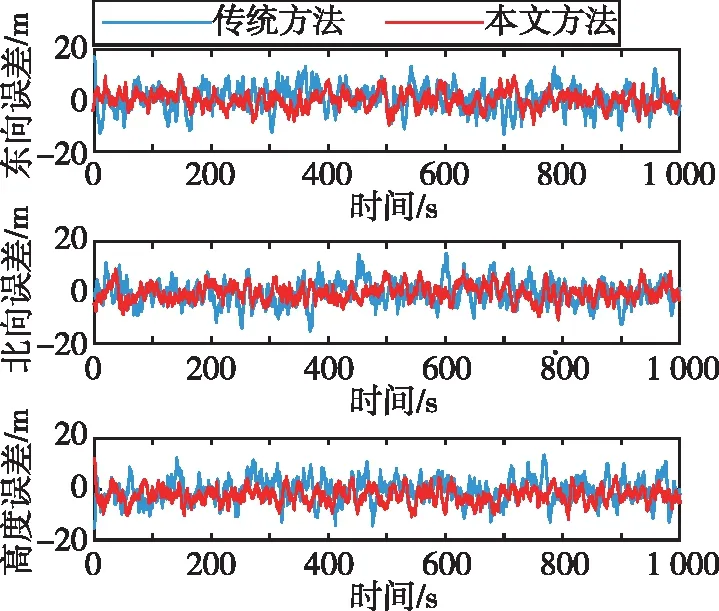
(a) 位置误差曲线比较

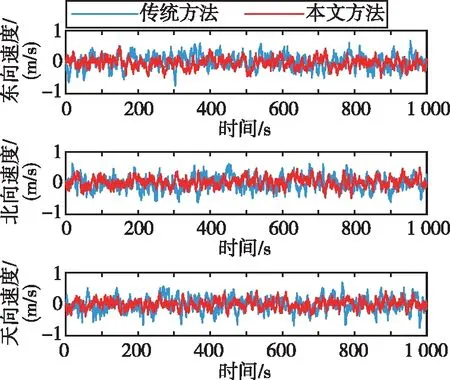
(b) 速度误差曲线比较

通过对比可知,当无故障发生时,本文算法的误差波动区间明显减小,曲线更为平缓,导航精度有所提升。因此,本文所述算法优于传统联邦滤波平均分配方法。

3.2 系统出现故障

模拟BDS出现故障的场景。由于BDS能提供位置和速度信息,因此分别对其位置信息和速度信息添加误差。

(1)BDS位置信息异常

在400 s时,在东、北、天3个方向上各施加30 m 的位置误差,该情况下本文算法的位置误差曲线如图3(a)所示;速度误差曲线如图3(b)所示。

(a) 出现位置故障时位置误差曲线

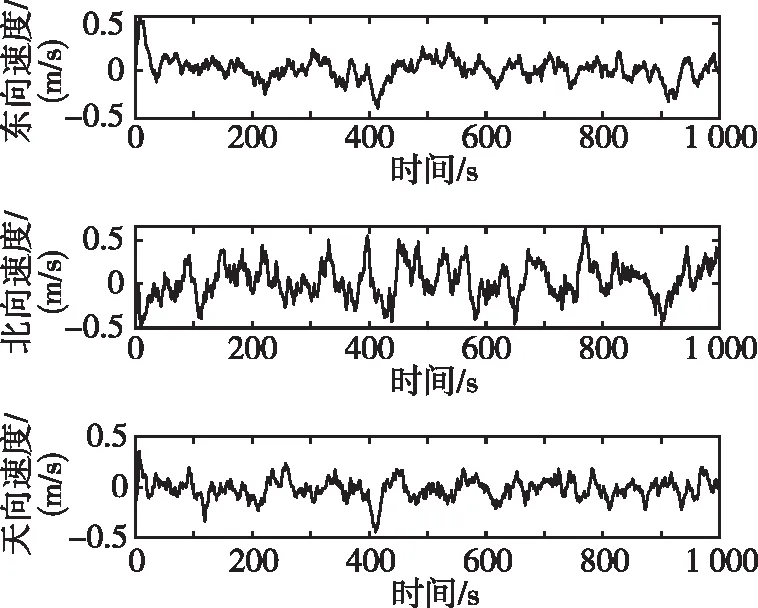
(b) 出现位置故障时速度误差曲线图3 出现位置故障时本文算法的误差曲线Fig.3 Error curves of the algorithm in this paper with failure of position

在图3(a)中,400 s时,3个方向上的位置误差突然增大,而后降为正常水平。由于系统可对BDS的导航信息分别检测和利用,当出现位置误差时,速度信息仍能在系统中发挥作用。因此,在图3(b)中,速度误差在该时间段内变化不明显,与其他时间段内持平。说明系统可以提高故障子系统中无故障信息的利用率。

(2)BDS速度信息异常

在600 s时,在东、北、天3个方向上各施加1.5 m/s 的速度误差,该情况下的本文算法的位置误差曲线如图4(a)所示;速度误差曲线如图4(b)所示。

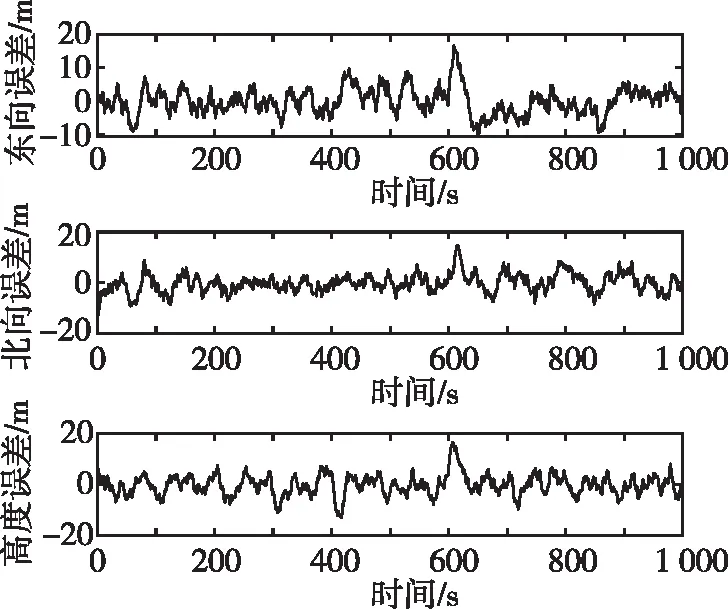
(a) 出现速度故障时位置误差曲线

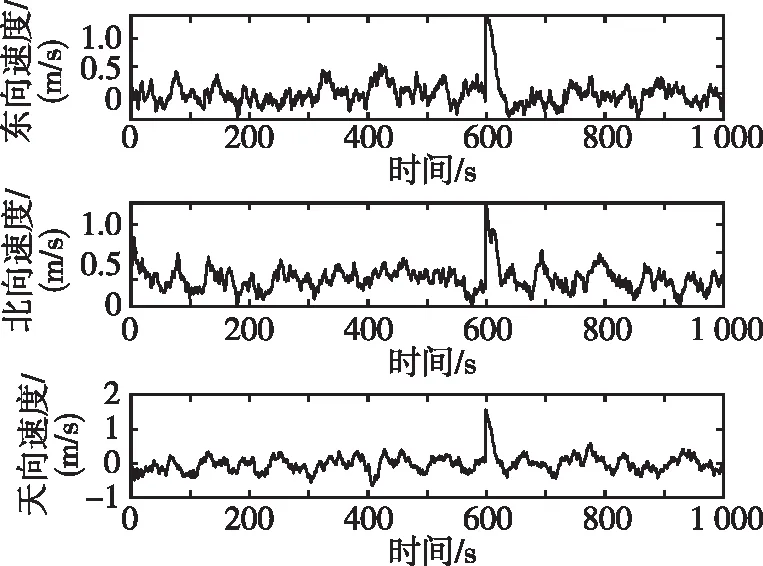
(b) 出现速度故障时速度误差曲线图4 出现速度故障时本文算法的误差曲线Fig.4 Error curves of the algorithm in this paper with failure of velocity

在图4(b)中,600 s时,3个方向上的速度误差突然增大,故障被隔离后误差降为正常水平。在图4(a)中,虽然系统可对异常的速度信息进行隔离,但检测需要一定时间,受此影响,在600 s左右位置误差有小幅度增加,而后由于故障信息被隔离,且BDS继续提供位置信息用于校正,故位置误差在一段时间后回归正常水平。由此可见,BDS所提供的无故障信息发挥了重要的作用。

(3)地磁罗盘故障

模拟地磁罗盘出现故障的场景。地磁罗盘能提供姿态角信息,但3个姿态角存在相关性。因此当其出现故障时需要对其进行整体隔离,以免故障扩散到整个系统中。在600 s时,在航向、俯仰、横滚3个方向上各施加0.2°的角度误差,该情况下本文算法的位置误差曲线如图5(a)所示;速度误差曲线如图5(b)所示;姿态角误差曲线如图5(c)所示。

(a) 地磁罗盘故障下位置误差曲线

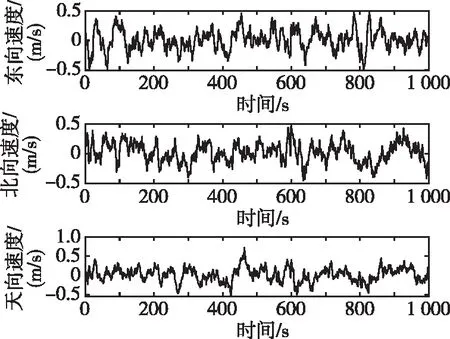
(b) 地磁罗盘故障下速度误差曲线

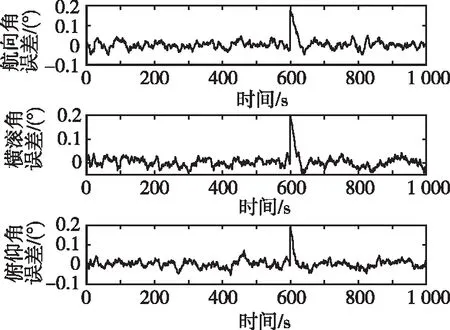
(c) 地磁罗盘故障下姿态角误差曲线图5 地磁罗盘故障下本文算法的误差曲线Fig.5 Error curves of the algorithm in this paper with failure of geomagnetic compass

在图5(c)中,角度误差增大后迅速下降,快速回归正常水平,表明故障信息被系统隔离。而在图5(a)和5(b)中,对应时间内,误差无明显变化,INS和BDS继续发挥作用,提供速度和位置信息。

4 结论

本文提出了一种基于矢量化检测联邦滤波的INS/BDS/地磁组合导航容错方法,实验结果表明,该方法可以提高系统在不同故障情况下的稳定性和鲁棒性。主要结论如下:

1)构建了面向不同导航信息的故障检测方法。针对BDS信息多,但易受干扰的特点,对其子系统的每个观测量均进行检测,在隔离故障信息的同时最大程度利用剩余的无故障信息,提高了信息利用率;针对地磁罗盘各观测量相关且误差对导航结果影响大的特点,对其组成的子系统使用计算量小的系统检测方式,快速检测隔离故障,防止误差扩散到整体系统中,提高了组合导航系统的鲁棒性。

2)通过使用矢量形式的信息分配方式来进行主滤波器的信息反馈,可以充分发挥各子系统的优点,并有效利用其中正常的状态估计信息,从而提高了整体组合导航系统的精度。

3)通过动态调整测量噪声矩阵,提高导航各子系统量测信息利用的可靠性,从而有效减小故障观测量对状态估计的影响。