全簧片式空间大行程并联柔性微定位平台及其轨迹控制
陈云壮, 赖磊捷*, 李朋志, 朱利民
(1.上海工程技术大学 机械与汽车工程学院,上海 松江 201620;2.格鲁斯特大学 计算与工程学院,英国 切尔滕纳姆 GL50 2RH;3.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;4.上海交通大学 机械与动力工程学院 机械系统与振动国家重点实验室,上海 200240)
1 引 言
微/纳米定位技术在纳米压印光刻、激光通信、生物细胞注射和快速反射镜等精密工程领域发挥着关键作用[1-3]。随着操作对象尺寸微型化、模型复杂化,使得对大行程多自由度微定位技术的需求越来越大。目前,微定位技术中经常使用的定位平台分为串联机构和并联机构。串联机构通过单自由度平台相互串联,使得误差被累积和放大,降低了运动精度,并且较大的惯性力不适用于高速定位场合[4]。并联机构通过并行的支链连接动/静平台,共同运动产生动平台的输出位姿,因其具有高负载、大刚度、低惯性和无累积误差等优点广泛用于大行程多自由度微定位平台的设计中[5]。此外,柔性机构通过柔性单元的弹性变形来传递力和运动,具有无摩擦、无装配误差和易加工等优点被广泛作为精密微位移传动机构[6]。当前,在基于压电陶瓷驱动器和并联柔性机构的多自由度纳米定位平台方面已经进行了大量的研究[7-8]。然而,由于压电陶瓷驱动器行程较小使得该类平台只能应用于小行程的定位场合。近期,音圈电机因其行程范围大、线性特性好、响应速度快等优点迅速成为大行程微定位平台的热门选择[9]。因此,基于音圈电机等电磁驱动的多自由度柔性微定位平台结构设计与控制研究受到越来越多的关注。
常见的多自由度微定位平台有平面三自由度(3-DOF)XYθZ平台[10]、空间平动XYZ平台[11-12]、空间3-DOFθXθYZ平台[13]和空间6-DOF平台[14]。其中以平面XYθZ平台最为广泛。例如:Yang[15]利用分布柔性的叶片柔性单元组成PPR运动链,设计了新型平面三自由度并联柔性机构,实现了±3 mm×±3 mm×±3°大范围平面运动。Awtar[12]则利用12组相同的平行四边形柔性模块进行正交组合实现10 mm×10 mm×10 mm大运动范围内的XYZ运动。但是针对空间偏转的3-DOF和6-DOF大行程微定位平台还鲜有报道。为满足激光通信和微操作机器人等领域的应用需求,空间3/6-DOF大行程纳米定位平台的研究也日益增多。近期,Kang[16]等利用音圈电机直接驱动由“蟹脚”柔性铰链组成的柔性机构来实现六自由度纳米定位,但由于采用了直驱方式,导致末端平台行程较小。Yang[17]等利用两组板簧弯曲叶片组成六个相似的音圈电机致动臂,设计了大范围高精度快速运行的六轴纳米定位器,但该平台未采用完全对称结构,仍具有较大的耦合。
为解决上述问题,本文设计了一种全簧片式的大行程并联柔性微定位平台。以实现3-DOFθXθYZ运动为例,该平台由四组相同的垂直致动臂并联组成,致动臂通过大行程簧片型柔性球铰与动平台相连使其能够实现三自由度空间解耦运动。首先,根据几何原理推导了机构运动学方程并作为控制回路的解耦矩阵。接着,分析了机构输入刚度并通过柔度矩阵法建立柔性球铰的柔度模型;然后,进行了系统动力学模型辨识,并基于辨识结果设计了含相位超前的PI反馈控制器同时结合滑模前馈控制消除相位误差进一步提高运动精度;最后,搭建实验平台,利用所设计的控制器通过单轴跟踪三角波轨迹和三轴联动跟踪圆柱形螺旋线轨迹来验证该机构和所设计控制器的轨迹跟踪性能。
2 柔性机构设计
图1为音圈电机驱动的多自由度大行程柔性并联机构。该机构由四组并联的全簧片致动臂、动平台(末端执行器)和静平台(基座)组成。致动臂包括平行四边形导向机构和柔性球铰,同时音圈电机被封装在平行四边形导向机构中以形成一个紧凑型设计,通过平行四边形机构中的两组大行程簧片弯曲变形传递力和运动。

图1 多自由度大行程柔性并联机构Fig.1 Multi-DOF long-stroke flexure parallel mechanism
柔性球铰的结构和变形原理如图2所示,同样利用分布柔度簧片的弯曲变形代替传统切口型铰链实现绕着X,Y和Z三轴大范围转动,克服了传统切口柔性铰链运动范围小,应力集中问题,同时提高了机构的刚度和稳定性。

图2 簧片型柔性球铰变形原理图Fig.2 Structural diagram of leaf-spring flexure spherical hinge
可见,本文所设计的柔性机构均采用分布柔度簧片,依靠其较大的变形,通过合理的排布,最终实现大行程多自由度的纳米定位。机构采用音圈电机直接驱动球铰而没有引入常见的位移放大机构,具有结构紧凑简单、运动链长度短,引入误差的参数少和精度高等优点。封装音圈电机的四组致动臂完全对称分布在动平台四周,并以差动形式工作,使得动平台可以实现Z方向的精密垂直运动和绕着X,Y轴精密偏转解耦运动。此外,如图1中的透明部分所示,在平台内部加入相同四组水平对称排布的致动臂,还可以实现动平台六自由度精密定位运动。
3 理论建模
3.1 运动学分析
图3为大行程柔性并联微定位平台的运动学模型。其中,OXY坐标系为全局坐标系,位于机构初始位姿动平台的几何中心。音圈电机及导向机构被简化为移动副,di(i=1~4)分别表示四个音圈电机的输出位移。不考虑音圈电机在往复运动过程中柔性球铰弹性变形引起X,Y方向的微小位移,即在动平台上仅有Z方向上的输入位移量。根据几何关系可以得到:
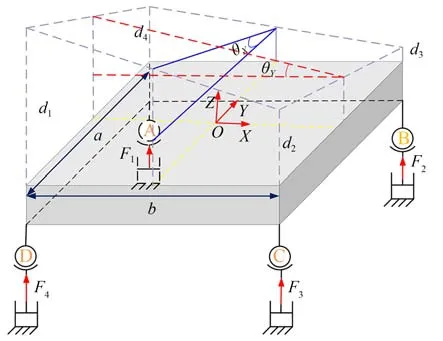
图3 微定位平台运动学模型Fig.3 Kinematic model of micro-positioning stage
可见,3-DOF柔性并联微定位平台系统为4输入3输出系统,存在输入冗余,因此需要加入约束条件才能实现电机力的均匀分配,防止局部过热等问题。本文采用均匀性分配原则[18],即竖直方向对角线上的两组电机产生的合推力相等,实现电流的平均分配,即:
其中,kin为机构单个致动臂的输入刚度。由于机构是完全对称的,所以各致动臂的输入刚度都相等。根据输入力的约束进而得到音圈电机位移量的约束条件为:
因此,该机构驱动关节空间与末端位姿的映射关系为:
3.2 输入刚度建模
音圈电机在致动臂输入端处施加推力FH,由于簧片尺寸相同,所以推力均匀分配到平行四边形机构中的两个簧片上。单簧片受力分析如图4所示。静力平衡时,由于弯矩M的反作用导致末端截面转角θ=0,因此可以得到:

图4 单柔性簧片受力分析Fig.4 Force analysis of clarinet
其中,截面惯性系数I=wt3/12。因此,音圈电机推力FH和弯矩M产生的挠度分别为:
结合式(5)和式(6)可以得到单个簧片在末端处最大位移量为:
由胡克定律可知,机构的刚度K为:
平行四边形导向机构中柔性簧片的尺寸为l=70 mm,w=18 mm和t=1 mm,利用公式(8)得到机构单个致动臂的输入刚度为7.5 N/mm。在音圈电机24 N的额定推力作用下,本文所设计的微定位平台理论上能够实现3.20 mm×21.33 mrad×21.33 mrad的运动范围,同时还可以计算得到动平台绕X/Y轴的转动刚度为676.06 N·m/rad。
3.3 柔性球铰柔度建模
动平台在音圈电机差分驱动下产生绕X/Y轴偏转,并利用柔性球铰来解耦各自由度方向上的运动。因此,柔性球铰的转动刚度需要进行合理设计,不能大于动平台在该方向上的转动刚度[19],否则会造成音圈电机驱动困难,行程变小且解耦效果不佳,同时也不能太小,否则会导致整个机构固有频率下降,承载能力降低[20]。本节基于柔度矩阵方法对柔性球铰进行了建模与设计。
簧片型柔性球铰结构示意图如图5所示,该球铰由7个柔性簧片组成。假设每个柔性簧片都有6个自由度,其变形量δ与外载荷F的关系为δ=CF。C为单个簧片的柔度矩阵[21]。为了得到球铰的转动刚度,将每个簧片的柔度统一等效到坐标系OA,坐标转换过程如下:
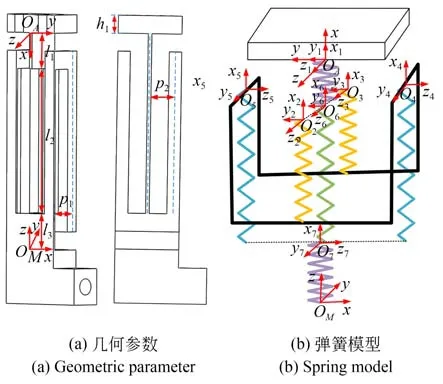
图5 簧片型柔性球铰结构示意图Fig.5 Structural diagram of leaf-spring flexure spherical hinge
其中:RAi和riA分别为簧片局部坐标系相对OA坐标系的旋转矩阵和位置矩阵,S为位置矩阵的反对称算子。由球铰弹簧模型图5(b)可见,簧片2和3并联,4和5并联,整体(2~5)与6并联,最后分别与1,7串联。根据串并联结构柔性模块的建模方法,整个球铰的柔度为:
通过反复调整簧片结构尺寸,并结合转动刚度的解析和仿真结果,最终确定柔性球铰尺寸参数如表1所示,计算相应的柔度列举在表2中。可见,球铰的转动刚度为0.94 N·m/rad,小于动平台的转动刚度,能够在满足音圈电机驱动的同时实现动平台运动解耦的设计要求。

表1 球铰尺寸参数Tab.1 Dimension parameters of spherical hinge
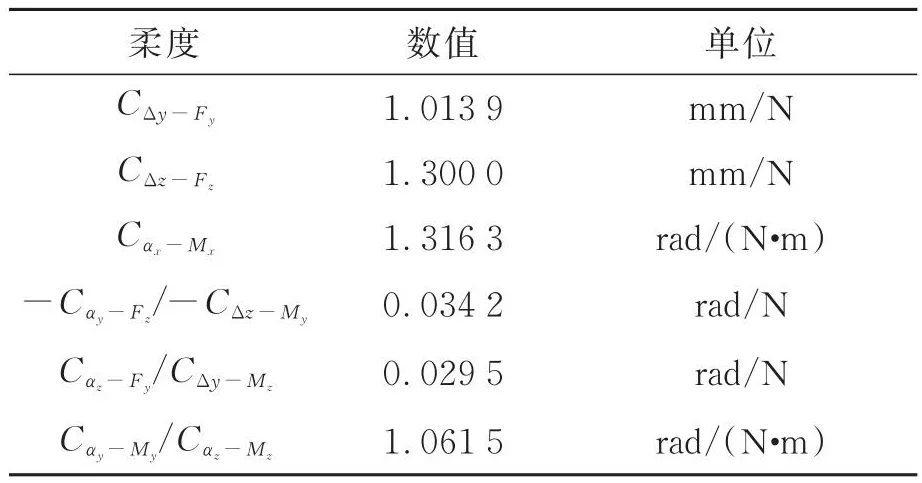
表2 簧片型球铰的柔度Tab.2 Compliance of leaf-spring spherical hinge
4 有限元验证
本节通过Ansys Workbench进行静力学分析来验证输入刚度计算的准确性。材料设置为铝合金,平行四边形导向机构簧片尺寸为l=70 mm,w=18 mm,t=1 mm,末端平台台面尺寸为a×b=300×300 (mm2)。如图6所示,通过对平行四边形导向机构沿Z轴正向施加24 N的载荷,同时保持其他三个致动臂不受限制,得到沿Z方向变形量为2.90 mm。因此,可得单个致动臂的输入刚度为8.27 N/mm。解析模型与有限元模型的计算结果偏差为9.31%,表明解析模型能够准确描述机构的静力学特性。
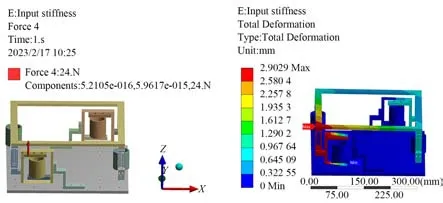
图6 输入刚度分析Fig.6 Input stiffness analysis
5 控制器设计
本文所设计的3-DOF并联柔性微定位平台是一个四输入三输出的输入冗余系统,并且还存在交叉轴耦合等现象致使平台的控制过程较为复杂。因此,本文通过在反馈回路中使用逆向运动学矩阵解耦该冗余系统,从而将多轴冗余控制转化为三个单输入单输出控制系统。本节还设计了一种相位超前比例积分(Phase Advanced Proportional Integral,PAPI)反馈控制器+滑动模态控制(Sliding Mode Control, SMC)的复合控制方法,其控制框图如图7所示。
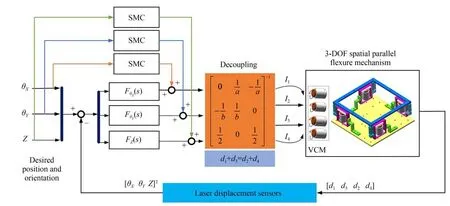
图7 多自由度微定位平台复合控制框图Fig.7 Composite control block diagram of multi-DOF micropositioning stage
5.1 系统辨识
首先,利用开环频域响应辨识系统在三自由度方向上的动力学模型。选择电压幅值0.005 V,0.005 V和0.5 V的Chirp信号分别作为辨识θX,θY和Z轴的输入信号,频率从0.1 Hz线性增加到300 Hz。借助MATLAB系统辨识工具箱ident对动平台的输入输出数据进行处理。以θY为例,辨识得到四阶传递函数如式(12)所示:
同时,还将动平台的Z向位移限制在0 mm,±0.5 mm,±2 mm五个不同的位置进行了系统辨识。图8显示了三个轴在不同工作点处动力学模型的主谐振频率基本一致。此外,θY轴和Z轴辨识传递函数模型G(s)与实际测量频率响应吻合度很高,仅θX轴在180 rad/s的高阶谐振附近存在差别,由于高阶谐振相比于主谐振对系统性能影响相对较小,因此在控制器设计中可以被合理的忽略。

图8 测量获得的频率响应与辨识结果Fig.8 Measured frequency response and identification results
5.2 含相位超前的PI控制器
图9中蓝色曲线为θY轴运动方向未校正系统的开环传递函数伯德图,由于系统的低阻尼谐振特性,该系统在幅值穿越频率附近的相位急剧下降(彩图见期刊电子版)。单纯使用传统PID控制器难以抵消相位快速下降对系统稳定性带来的影响[22]。因此,为了使动平台具有更好的轨迹跟踪性能,设计相位超前校正控制器来提高系统的相位裕量,使得动平台满足稳定性的要求。这里仅以θY轴为例,θX和Z轴以相同的方法得到。
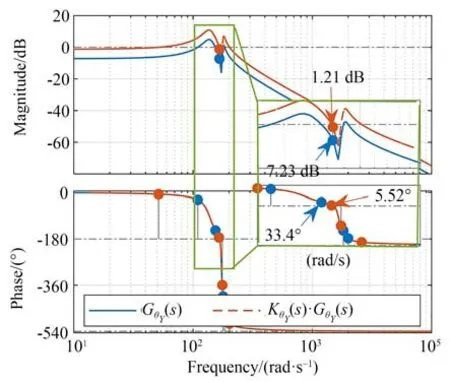
图9 开环增益调整前后未校正系统的幅值和相位裕量Fig.9 Amplitude and phase margin of uncorrected system before and after open-loop gain adjustment
首先,根据校正前系统开环增益和校正后系统的静态速度偏差要求[22],暂定控制器增益=2。增益调整前后未校正系统的伯德图如图9所示,可见增益调整后系统当前的相位裕量为5.52°。设定期望的相位裕量γθY=60∘,因此超前校正控制器的相位超前角ϕθY为:
因此,可得增益为-10lg (1)对应的校正后系统幅值穿越频率为629.4 rad/s。求得转角频率对应的时间常数为:
因此,得到θY轴方向的相位超前控制器为:
为了进一步减小系统的稳态误差,在相位超前环节的基础加上增加了PI控制器。在积分环节中选择时间常数T=0.02,同时调整PI控制器相应的增益cθY为0.63,以减少积分环节对系统相位裕量的影响[23]。最终得到含相位超前环节的PI反馈控制器如式(17)所示:
图10显示了加入含相位超前环节PI控制器后系统的开环传递函数伯德图。可见,校正后开环系统的幅值和相位裕量分别大于6 dB和60°,因此能够满足该多自由度并联微定位平台的稳定性要求。
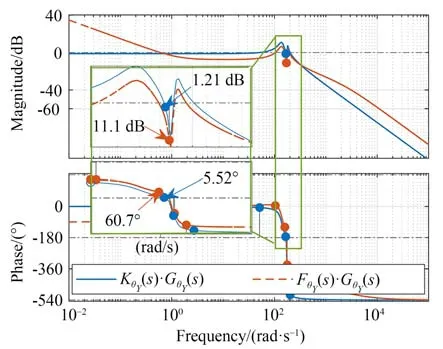
图10 加入含相位超前PI控制器后系统开环伯德图Fig.10 Open loop bode diagram of the system after adding PI controller with phase advanced
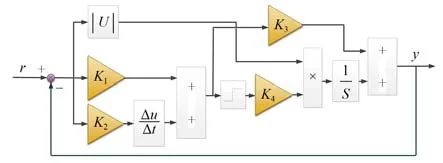
图11 SMC控制框图Fig.11 SMC control block diagram
5.3 滑模控制器
滑模控制可以根据动态条件改变控制对象的控制状态,同时具有快速响应、对控制对象参数变化及干扰条件不灵敏等优点,因此,在PAPI控制的基础上引入了SMC前馈控制,可以有效提高平台的响应速度和精度。SMC控制框图如11所示,其应用的关键是选择滑模面(S)并建立稳定的设计控制律。本节设计的是一个二阶滑模面,并以幂级数的形式设计了控制律如式(18):
其中:K1和K2为滑动面参数,决定于系统的刚度和阻尼。K1的增加将有效提高系统的控制刚度和响应速度,调节K2可以改变系统的阻尼。K3和K4为控制律参数,用于微调系统。当达到可接受的动态性能时,调整K3和K4可以减少系统的跟踪误差。本文滑模控制器中的参数K1,K2,K3和K4分别设置为15,1,0.15和0.15。
6 系统搭建与轨迹跟踪实验
6.1 微定位平台系统搭建
首先,搭建了如图12所示的实验系统。该系统由柔性并联微定位平台、半实物实时仿真系统、以及位移测量与信号采集系统组成。微定位平台选用四个音圈电机(VCAR0070-0419-00A)作为机构驱动器产生输入位移。Simulink中的半实物实时仿真系统控制2块数据采集卡(PCI-6221)的四个模拟输出端口输出电压(-10~10 V),经过四个线性放大器(TA115)后线性转换为音圈电机的驱动电流(-2~+2 A),输入到音圈电机。位移测量系统采用激光位移传感器(HL-G103-S-J),分辨率为0.5 μm,测量范围为±4 mm对应(0~10 V),由数据采集卡的模拟输入进行采集实现闭环反馈。
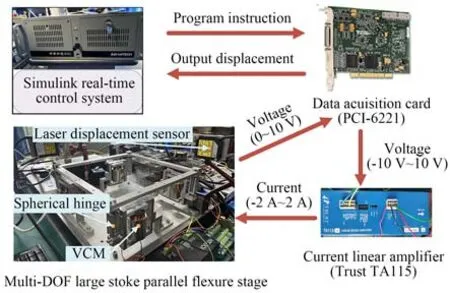
图12 微定位平台实验系统Fig.12 Experimental system of micro-positioning stage
6.2 开环行程与耦合测试
给定每个音圈电机电流让其产生24 N额定的持续推力,在差分驱动方式下进行开环实验测试得到微定位平台的最大行程为3.23 mm×21.50 mrad×20.30 mrad,如图13所示。实验与理论计算结果误差为0.9%×0.79%×4.8%,表明了建模的准确性。此外,还通过开环测试实验得到了平台的轴间耦合误差,如图14所示,以θY为例,θY轴在10 mrad范围内运动时,会在Z轴和θX轴上分别产生0.106 mm和0.853 mrad的最大耦合误差,可见开环控制下,产生的θX轴耦合误差约占θY轴运动行程范围的8.53%。
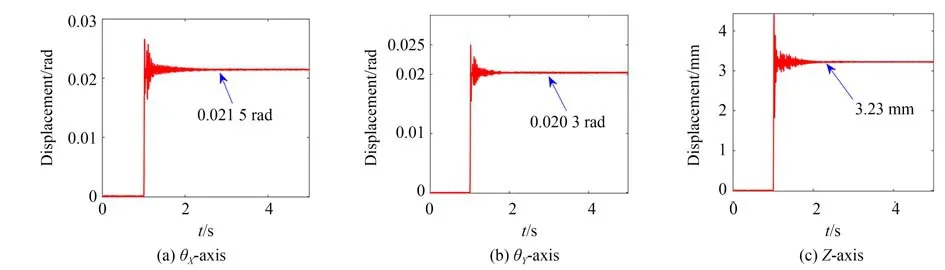
图13 最大行程Fig.13 Maximum stroke

图14 轴间耦合误差Fig.14 Cross-axis coupling errors
6.3 轨迹跟踪实验
本节通过单轴驱动跟踪三角波轨迹、三轴联合驱动跟踪圆柱形螺旋线轨迹来研究该平台的轨迹跟踪性能。首先,在θX,θY和Z三个自由度方向上分别使用PID,PAPI和PAPI+SMC三种控制方法对三角波信号进行轨迹跟踪,对比结果如图15所示。轨迹跟踪的平均绝对误差(Mean Absolute Error,MAE)和均方根误差(Root Mean Square Error,RMSE)如表3所示。基于MAE结果,与传统PID相比,所提出的PAPI+SMC控制使得θX,θY和Z轴跟踪性能分别提高了96.36%,98.25%和96.5%。

表3 微定位平台单轴轨迹跟踪性能(三角波轨迹)Tab.3 Single-axis trajectory tracking performance of micro-positioning stage(Triangular wave track)
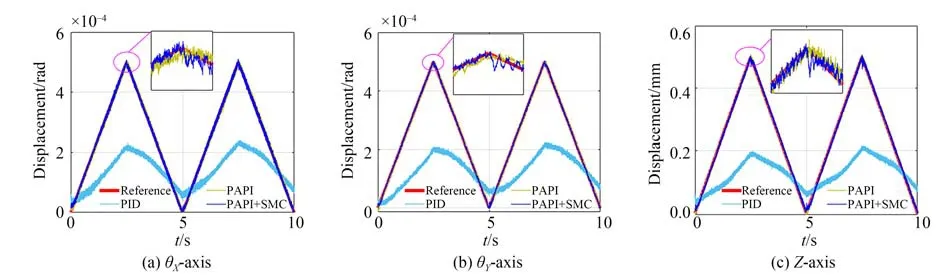
图15 三角波轨迹跟踪结果Fig.15 Triangular wave track tracking results
最后,通过三轴联合驱动研究微定位平台对空间圆柱螺旋线轨迹的跟踪性能。在θX,θY和Z轴上,圆柱螺旋线轨迹范围分别是±5 mrad,±5 mrad,±1 mm,跟踪响应结果和相应的跟踪误差如图16所示。

图16 空间圆柱螺旋线轨迹跟踪结果Fig.16 Space cylindrical spiral track tracking results
同时还分别计算了轨迹跟踪MAE和RMSE,结果如表4所示。可以看出,与PAPI相比,PAPI+SMC显示出更好的跟踪效果,并且基于MAE结果,PAPI+SMC复合控制使得θX,θY和Z轴跟踪性能分别提高了78.6%,79.0%和0.2%。其中,对Z轴跟踪性能没有提高是因为Z轴跟踪轨迹是直线,达到稳态后几乎没有稳态误差。通过轨迹跟踪实验可以得出结论,在跟踪三角波轨迹时,与经典的PID控制相比,PAPI和PAPI+SMC显著提高了跟踪性能,并且加入SMC后能够有效消除PAPI控制产生的相位误差,进一步提高了跟踪精度。在跟踪圆柱螺旋线轨迹时,所提出的机构能够以高精度和较小误差跟踪给定轨迹。

表4 微定位平台三轴空间轨迹跟踪性能(圆柱螺旋线轨迹)Tab.4 Three-axis spatial trajectory tracking performance of micro-positioning stage(Cylindrical spiral track)
7 结 论
本文根据精密工程领域中微定位平台大行程、多自由度的需求,提出了一种音圈电机驱动的全簧片式大行程多自由度空间柔性并联微定位平台。首先,根据几何原理推导了动平台的运动学方程,并作为控制回路的解耦矩阵。接着,建立了机构输入刚度模型并仿真验证了模型的准确性。其次,基于柔度矩阵法对柔性球铰进行了柔度建模和设计,从而确定了微定位平台结构参数。然后,对三自由度方向进行了系统动力学模型辨识,基于辨识模型设计了PAPI反馈控制器并结合SMC前馈构成复合控制。最后,搭建了音圈电机驱动的微定位平台系统验证其轨迹跟踪性能。实验结果证明:与PID控制相比,PAPI+SMC复合控制使得跟踪性能提高了95%以上,同时有效消除了单纯PAPI控制产生的相位滞后。并且,所提出的多自由度柔性并联微定位平台具有行程大、稳定性好和精度高等特点,能够以高精度和小误差跟踪空间给定轨迹,可以用于许多需要空间大行程高精度的应用场合。

