复合冲击作用下PDC 钻齿破岩过程连续-非连续数值模拟研究

秦承帅，孙洪斌，李利平，刘学港，刘知辉，冯 春，孙子正,4

(1.山东大学 齐鲁交通学院，山东 济南 250002；2.山东铁路投资控股集团有限公司，山东 济南 250001；3.中国科学院力学研究所，北京 100084；4.山东大学 深圳研究院，广东 深圳 518057)

定向钻进技术具有长距离精准穿越的优势，常应用于隧道工程地质勘察及灾害处置、煤矿底板含水层改造等领域。伴随交通强国、“一带一路”倡议等国家重大战略的实施，我国已成为世界上隧道建设数量、规模最大和难度最高的国家。截至2022 年底，我国已建成交通隧道、水工隧洞等逾7.69 万km[1]，定向钻进技术在隧道工程领域拥有广泛的发展前景。

隧道工程地质勘察与灾害处置对钻进速度要求较高，作业迟缓会导致影响工期进度，特别是在灾害处置过程中易造成受灾影响范围扩大，引发次生灾害等问题[2-4]。为提高定向钻在钻进过程中的破岩效率，国内外学者围绕轴向冲击、扭转冲击和复合冲击等新型破岩方式进行了研究。其中，复合冲击钻进是指兼具轴向和扭转2 个维度冲击的新型破岩技术，复合冲击钻进可实现多元“立体破岩”效果[5]。在复合冲击钻具的研发方面，国内外众多学者研发了可实现往复扭转冲击和高频轴向冲击的复合冲击钻具[6-8]，该种钻具可在不改变其他设备参数的基础上通过施加高频低幅的冲击作用形式进一步提高钻进速率[9-11]。在钻头破岩机理方面，围绕岩石的破碎过程、裂纹的萌生和扩展规律以及岩石破碎的动力学特性等方面开展的研究较多[12-14]，如岩石在冲击作用下的破碎区域可分为岩石破碎区、岩石剥离区和裂纹扩展区[15-16]，岩石的破碎过程通常是单个裂纹萌生和扩展的结果，且在卸荷阶段产生的侧向裂纹更利于岩石的去除等[17-19]。在快速钻进破岩数值模拟研究方面，当前，围绕岩石力学所开展的数值模拟分析方法主要分为两大类[20-22]：第一类是以连续介质力学为代表的分析方法，如有限元法、有限差分法等[23-26]，第二类是以非连续介质力学为代表的分析方法，如颗粒离散元法、块体离散元等[27-28]。当前，基于数值模拟方法开展的研究，多通过建立钻齿-岩石动力冲击下的数值模型来分析岩石在不同钻进参数下的破坏效果[11,29]。但连续类或非连续类的分析方法都难以模拟岩石从连续介质到非连续介质的损伤演化过程[30-32]。

综上，对已有成果的调研发现，复合冲击钻进技术在提高钻进效率方面具有显著的优势。但当前的研究成果多基于岩石受单向冲击作用下开展的，而对于钻头在复合冲击作用下的破岩机理研究较少。笔者通过连续-非连续分析方法，开展了聚晶金刚石复合片钻头(Polycrystalline Diamod Compact，PDC)单钻齿复合冲击破岩过程模拟。基于对岩石岩屑、径向剪切裂纹、侧向裂纹和侧向主裂纹等形成过程的分析，揭示岩石在复合冲击作用下的破坏规律。在此基础上，分析钻齿的轴向、扭向冲击参数与齿-岩接触参数对破岩效果的影响及冲击能量的分布效果，以期对提高破岩效率、优化钻齿设计参数、延长钻具使用寿命等提供借鉴。

1 连续-非连续分析计算模型与实验验证

采用连续-非连续单元法，通过建立基于共享节点的FEM-DEM 耦合模型，研究岩石在复合冲击作用下从连续介质到非连续介质的损伤演化过程，并进一步分析复合冲击作用参数对岩石的破坏影响规律。

1.1 连续-非连续单元法理论基础

基于连续-非连续单元法的理论基础为广义的拉格朗日方程，其能量体系[10]表达式为：

式中：L为拉格朗日函数；uj为单元的节点位移；为单元的节点速度；Qj为系统非保守力；t为时间。拉格朗日函数可写为L=Πm+Πe+Πf，其中 Πm、Πe、Πf分别为系统动能、弹性能和势能。

广义拉格朗日方程表达式最终可表示为：

式中：M为单元质量矩阵；C为单元的阻尼矩阵；K为单元的刚度矩阵；F为外部荷载向量；(t)为单元节点的加速度；(t)为 单元节点的速度；u(t)为节点的位移。

基于GDEM 软件BlockDyna 和PDyna 模块开展研究。GDEM-BlockDyna 模块中包含了块体和界面2 个概念，计算模型的构成如图1 所示。块体是由一个或多个连续介质单元组成，可用于表征连续介质体的弹性、塑性等物理特征。界面包括真实界面和虚拟界面两类：真实界面指2 个块体之间真实存在的界面，一般为固体材料的分界面、结构面和接触面等；虚拟界面指存在于块体单元中的潜在扩展通道，当块体不发生破坏时，虚拟界面仅起到传递力的作用[11]。

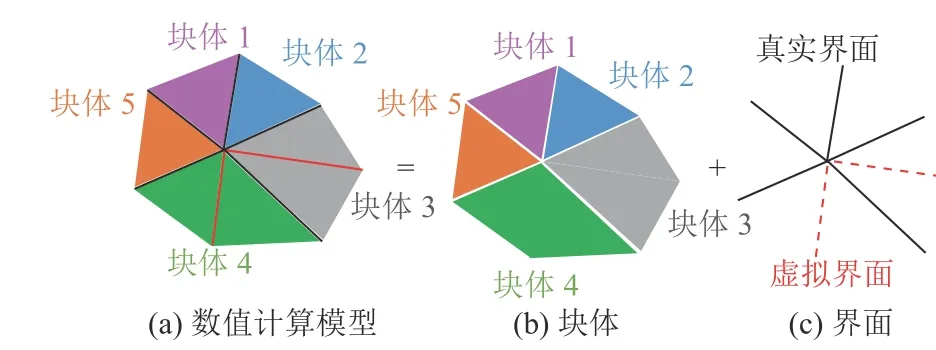
图1 BlockDyna 计算模型Fig.1 BlockDyna calculation model

颗粒动力学仿真系统(GDEM-PDyna)，以颗粒离散元方法为主。颗粒运动及受力状态如图2 所示，通过颗粒间的合力及合力矩的计算，进一步计算颗粒的运动及转动状态。颗粒的合力及合力矩的计算公式为：

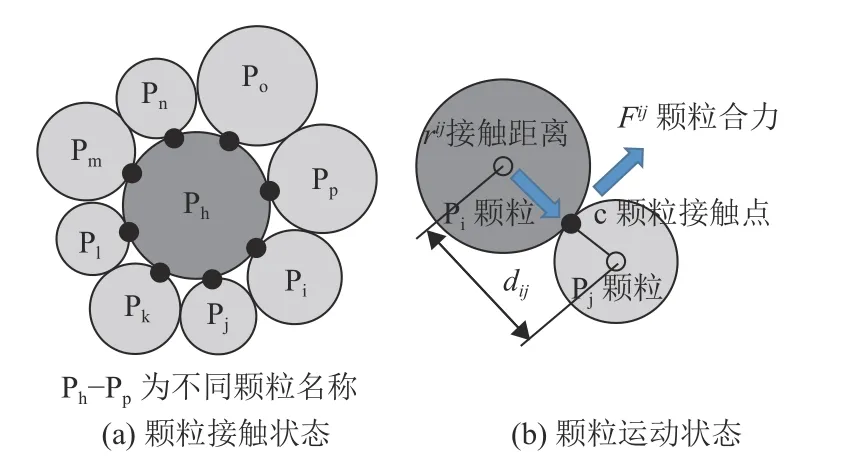
图2 颗粒接触及运动状态Fig.2 Particle contact and motion state

由颗粒合力及合力矩可计算颗粒的运动状态，颗粒的运动包含平动和转动2 种，平动运动方程具体可表示为：

1.2 基于共享节点的FEM-DEM 耦合模型

基于GDEM 软件的BlockDyna 和PDyna 模块，建立了基于共享节点的FEM-DEM 耦合模型，该模型将有限元的单元与离散元的颗粒通过共享节点进行有机耦合，如图3 所示。其中，共享节点承载了模型的动能及势能，在计算过程中通过块体-颗粒耦合转化过程，可精确模拟固体材料从连续介质到非连续介质的过渡过程。

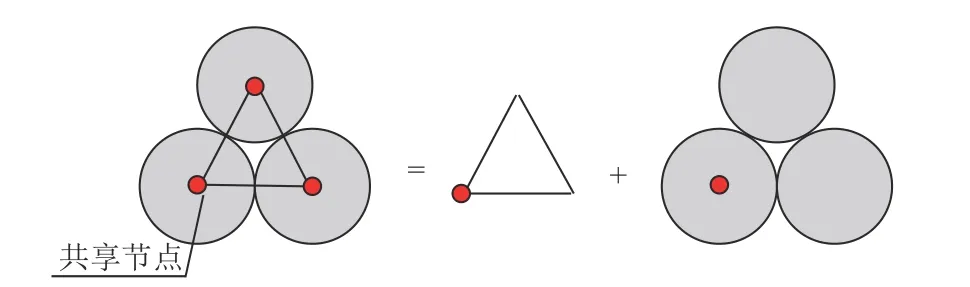
图3 基于共享节点的FEM-DEM 耦合模型原理Fig.3 Principle of FEM-DEM coupling model based on shared node

基于共享节点的FEM-DEM 耦合模型的建立过程如图4 所示。首先，建立有限元模型；其次，基于有限元节点创建离散元颗粒体系；最后二者通过共享节点进行有机耦合。

图4 基于共享节点的FEM-DEM 耦合模型建模过程Fig.4 Modeling process of FEM-DEM coupling model based on shared nodes

在该模型计算过程中，有限元和离散元计算体系可分别进行独立计算，二者通过贡献因子进行有机结合，其计算原理图如图5 所示。

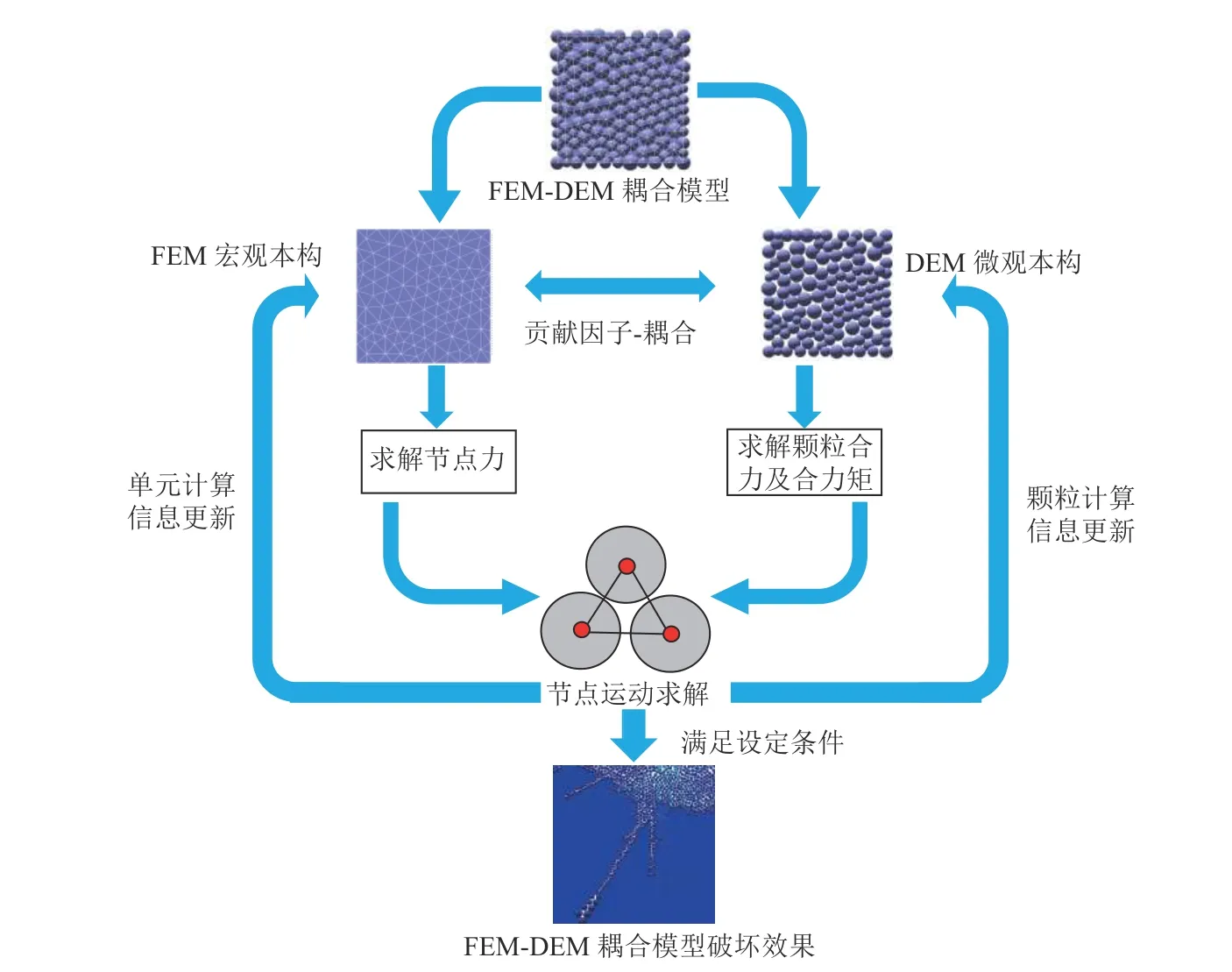
图5 基于共享节点的FEM-DEM 耦合模型计算流程Fig.5 Calculation flowchart of FEM-DEM coupling model based on shared nodes

1.3 室内实验及模型验证

本文通过室内单轴压缩实验对计算模型进行试验验证。为分析复合冲击钻头在硬岩地层的破岩效果，以坚硬的黄砂岩为实验材料，并根据岩石力学实验规范，采用直径为50 mm、高度为100 mm 的标准岩石圆柱形试件。单轴压缩实验仪器采用多功能岩石直剪实验机。该实验机在国内外现有产品基础上采用双路交流伺服电机驱动技术、传感器技术、微机控制技术和软件处理技术等，可用于岩石本身及其结构面的压缩及直剪实验。该实验机最大实验力可达300 kN，力值测量精度为±0.1%示值，位移测量精度为±0.5%示值，该设备完全满足本实验的要求，如图6 所示。

图6 室内单轴压缩实验Fig.6 Laboratory uniaxial compression experiment

在室内实验基础上，基于建立的共享节点FEMDEM 耦合模型，对黄砂岩的单轴压缩破坏过程进行了模拟分析，其建模过程如图7 中所示。

图7 基于共享节点的FEM-DEM 耦合单轴压缩模型Fig.7 FEM-DEM coupling uniaxial compression model based on shared nodes

岩石材料参数赋值见表1。数值计算结果和室内实验对比效果如图8 所示，根据图中对比效果可发现，岩石试件在数值模拟和室内实验中均发生斜截面剪切破坏。

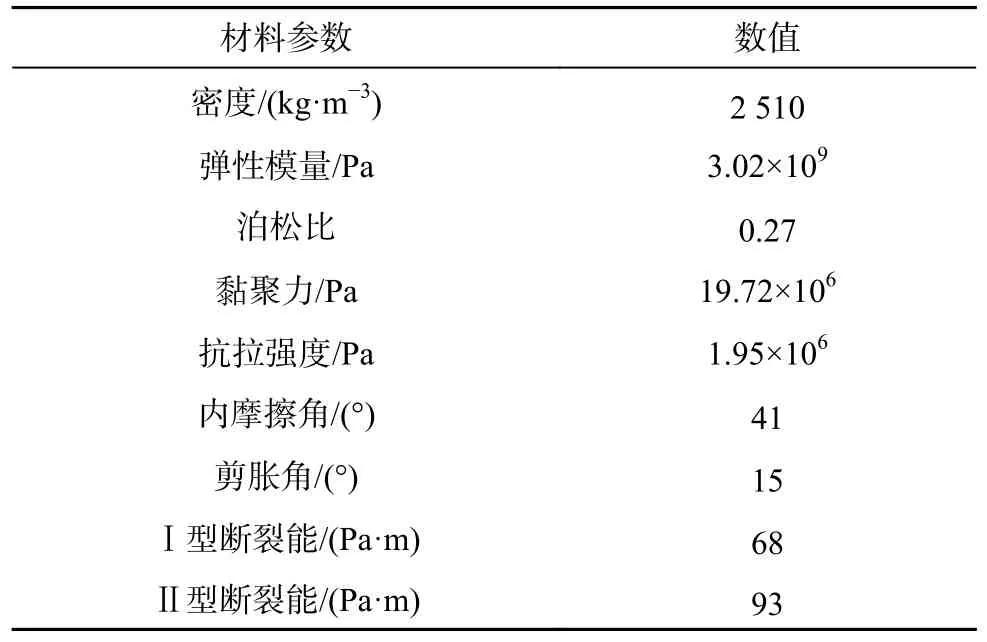
表1 岩石材料参数Table 1 Rock material parameter

图8 岩石单轴压缩破坏过程模拟Fig.8 Failure process simulation of rock under uniaxial compression

数值模拟和实验结果中的对比效果如图9 所示，岩石试件的破坏过程经历了孔隙压密、线弹性、非稳定破坏发展、破坏后阶段，上述岩石在单轴抗压下的损伤演化过程符合岩石力学中所描述的岩石破坏规律。通过对比可发现，室内实验和数值模拟结果具有较好的吻合性，同时也证明本模型在岩石损伤破坏模拟过程中的合理性。

图9 数值模拟和室内实验应力-应变曲线对比Fig.9 Comparison of stress-strain curves between numerical simulation and laboratory experiment

2 定向钻复合冲击破岩机制

为研究定向钻复合冲击破岩机制，基于连续-非连续分析方法，建立单钻齿复合冲击破岩模型，并对影响复合冲击破岩规律的参数进行总结分析。

2.1 单钻齿复合冲击破岩模型

在复合冲击破岩钻进过程中，冲击钻具直接作用在PDC 钻头上，钻头同时受轴向冲击和扭转冲击的共同作用。为了更加有效的观察岩石在复合冲击作用下的裂纹萌生和扩展过程，建立了如图10 所示的复合冲击单齿侵入破岩模型，并采用线性正交切削法对岩石进行破岩过程模拟。

图10 单齿侵入破岩数值模型Fig.10 Numerical model of rock breaking by single bit drilling

如图10a 所示，该模型沿中心取纵剖面进行分析，岩石模型的尺寸为40 mm×23 mm(长×宽)，相应地，钻齿模型的尺寸为10 mm×5 mm(长×宽)，将刀具的后倾角γ设为15°，钻齿吃入岩层的深度设为Δh=3 mm，具体数值模拟模型如图10b 所示。

所建立的岩石数值计算模型如图11 所示，首先在商业软件ABAQUS 中进行模型的初步构建和单元的离散，如图11a 所示。在网格划分时，为了保证模型的计算精度，同时提高计算效率，因此，对岩石模型的上半部分进行了局部加密处理，处理效果如图11b 所示。

图11 基于共享节点的FEM-DEM 岩石模型及创建过程Fig.11 FEM-DEM rock model based on shared nodes and its creation process

在网格局部加密时，为了保证加密网格的尺寸更加符合岩石颗粒尺寸，本模型采用0.2 mm 的网格尺寸作为加密网格尺寸。所建立模型共含节点11 711 个，CPS3 类型块体23 086 个，离散元颗粒11 711 个，颗粒体积为8.55×10-4m3，岩石材料模型参数与1.2 节中的参数保持一致。

2.2 复合冲击破岩模型边界条件

在模型计算过程中，将岩石的左右边界和底部边界固定，上部边界则设定为自由边界，用于模拟岩石的切削和岩屑的形成过程。

将刀齿设定为刚性体，在此基础上分析钻齿不考虑静载条件下的复合冲击过程。将钻头运动过程中的复合冲击速度分解为扭转冲击速度vx和轴向冲击速度vy，如图12 所示。

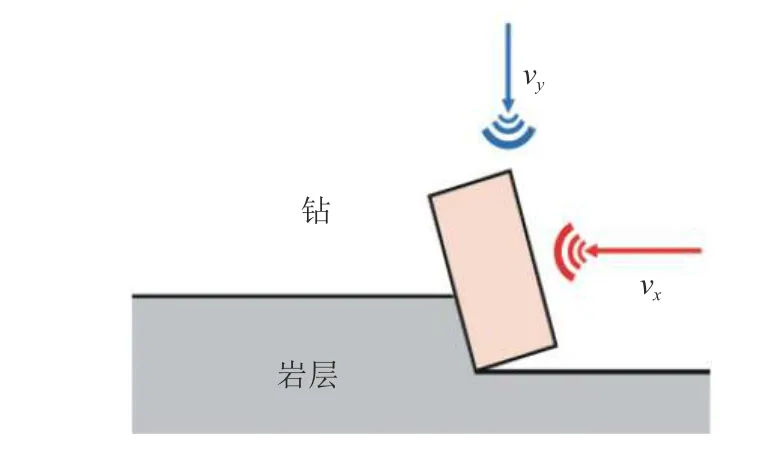
图12 复合冲击速度分解Fig.12 Decomposition of composite impact velocity

在GDEM 计算平台中难以通过现有的命令进行周期性函数的施加，为分析单钻齿的复合冲击破岩过程，本文基于JavaScript 脚本命令对计算程序进行了二次开发，其过程如下：

(1)设定当前计算时间为0。

(2)计算前初始化设置，核心迭代前调用dyna.BeforeCal()函数。

(3)设定for 循环计算命令，钻齿运动速度的改变在此循环中实现。

(4)通过dyna.GetValue()函数，获取当前的计算时间Time_Now 信息。

(5)基于步骤(4)获取的当前计算时间，设定钻齿的运动速度，此时速度值为随时间变化的周期性正弦函数，设定冲击作用周期为2 ms，设定冲击速度分别为vx=0.2sin500π，vy=0.5sin500π，如图13 所示。

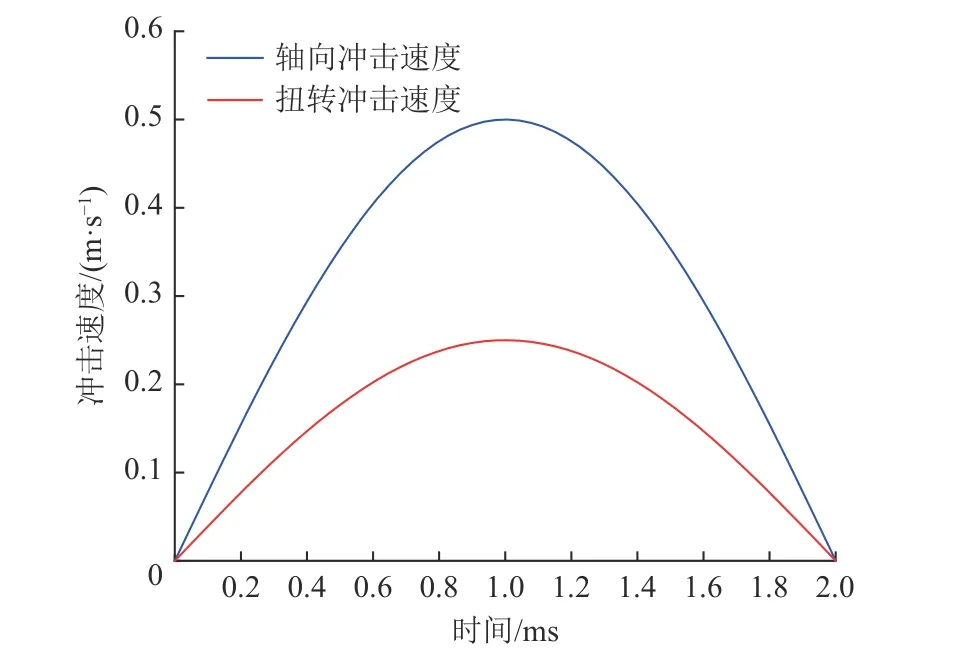
图13 钻齿运动速度Fig.13 Motion speed of drill bit

(6)通过rdface.SetElemValue()函数，将步骤(5)所设定的当前运动速度赋值给钻齿。

(7)设定模型的虚拟质量开关、时步计算的比例因子和数据后处理监测信息等。

(8)设定迭代求解命令，该过程为单一迭代步求解，整个过程包含时间及时步的累加，但不包含云图信息和监测信息输出等。

(9)计算结束及结果推送，步骤(1)—步骤(8)为整个核心求解过程，该步骤则将计算信息推送至GDEM计算平台。

2.3 复合冲击破岩规律

基于上文的数值计算模型，复合冲击破岩计算过程分2 个阶段：(1)在不施加钻齿的前阶段，将钻齿模型设定为空模型，并对岩石模型进行自重力场的求解，当计算的不平衡率≤10-5时结束该过程求解。(2)设定并激活钻齿模型，同时施加设定的冲击速度，进行复合冲击破岩过程模拟，如图14 所示。

图14 岩石模型自重力求解Fig.14 Self-granvity solution of rock model

图15 为模拟岩石在单次复合冲击作用下的破碎过程。在初始阶段，钻齿与岩石相接触，如图15a 所示，在0.23 ms 左右时，钻齿前方及下方的应力逐渐增大，岩石进入塑性状态。在0.62 ms 左右时，岩石开始出现损伤破坏，并在钻齿的尖端及前方产生微裂纹，如图15b 所示。冲击作用的初始阶段使岩石产生初步损伤，为后续裂纹的萌生扩展和破碎坑的形成创造了前提条件。

图15 复合冲击破岩过程模拟Fig.15 Simulation of rock breaking process under composite impact

随着轴向冲击速度和扭转冲击速度的增加，钻齿开始压缩下方岩石，钻齿与岩石接触点的应力逐渐增大，在0.77 ms 左右时，微裂纹开始向岩石的内部进一步扩展，如图15c 所示。当复合冲击速度达到最大值，在1.13 ms 左右时，钻齿前方和下方的岩石开始发生破碎，并形成破碎区和破碎坑，且钻齿下方的裂纹逐渐向岩石的内部逐渐发展，如图15d 所示。复合冲击作用加速了裂纹的萌生和扩展，裂纹的进一步发展是破碎坑形成的主要原因。

在1.22 ms 左右时，如图15e 所示，由于岩石内部积累的能量被迅速释放，岩石的最大应力集中于破碎区附近，此时，内部裂纹逐渐扩展延伸到岩石表面，形成侧向裂纹和剪切裂纹，钻齿下方的岩石被压缩破坏，形成较大的岩石碎屑和破碎坑。岩石由于张拉破坏形成的裂纹扩展到岩石表面，进一步加大了岩石破碎坑的形成。在1.45 ms 左右时，岩石内部形成的侧向裂纹和剪切裂纹逐渐贯通至岩石上部的自由表面，岩石发生大面积的剪切破坏，并形成大量碎屑，此阶段岩石碎屑体积仍较大。分析1.22～1.45 ms 的作用过程可发现，复合冲击作用加速了侧向和剪切裂纹向自由面贯通的过程，并且促进了大块岩屑的形成。

最后阶段，在1.68 ms 左右时，如图15g 所示，大块岩屑在冲击作用下开始破碎形成小岩屑，破碎坑内的岩屑与岩石表面剥离，达到破岩效果。在1.92 ms左右时，如图15h 所示，与钻齿接触的岩石部分基本已在冲击作用下发生破碎，岩石的损伤区域逐渐向内部延伸。但分析1.68～1.92 ms 的作用过程也可发现，在该过程中，岩石的破碎区和裂纹的发展趋势并无明显变化，这说明钻齿难以进一步向下破碎岩石。

复合冲击作用的整个过程是能量的积累和释放的过程，在该过程中，复合冲击作用使钻齿尖端附近积蓄大量能量，而能量的释放则造成了裂纹的萌生扩展和贯通，进而产生破碎坑。

在复合冲击作用下，岩石首先会出现预损伤，随后产生微裂纹。随着冲击速度的增大，微裂纹逐渐发展形成较大裂纹，并形成岩屑。最后较大裂纹逐渐贯通至岩石自由表面，形成剪切破坏区域。与此同时，岩石的损伤破坏区域逐渐向岩石内部扩展，为下一次岩石破碎做准备。在此过程中，钻齿的前方和下方的岩石均被破碎，形成了“立体破岩”效果，如图16 所示。

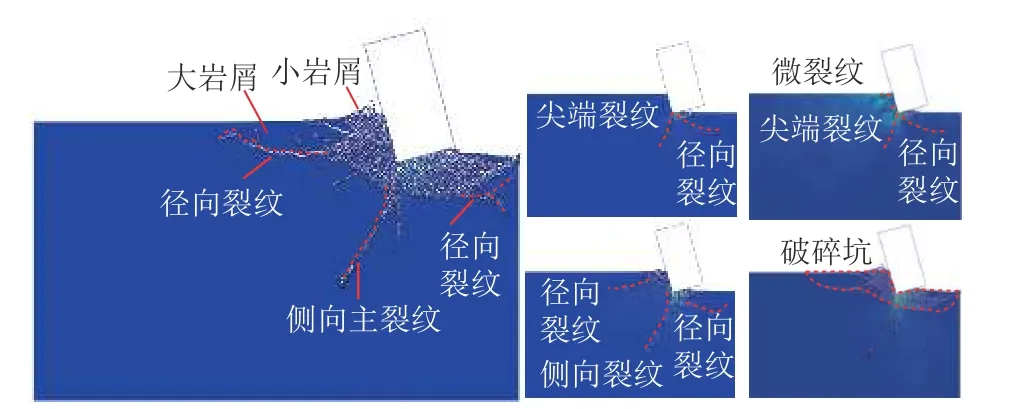
图16 岩屑形成及裂纹扩展规律Fig.16 Debris formation and crack propagation law

上文分析了单钻齿的复合冲击破岩过程，通过分析发现，该过程主要是促进了裂纹的萌生扩展和破碎坑的形成。复合冲击下岩石的破碎主要分为4 个阶段：(1)裂纹产生阶段，该阶段主要是尖端裂纹的产生和微裂纹的萌生和扩展，岩石开始产生初步损伤；(2)裂纹扩展阶段，在该过程中，岩石内部的微裂纹进一步发展，并形成侧向裂纹和剪切裂纹等；(3)破碎区形成阶段，侧向裂纹和剪切裂纹逐渐发展并贯通至岩石的自由表面，形成破碎坑和大块岩屑，同时岩石内部的剪切裂纹和侧向裂纹有逐步向岩石内部发展的趋势；(4)岩屑剥离阶段，在该阶段中，大块岩屑被冲击撞碎形成较小岩屑，岩石发生拉剪破坏形成破碎坑，岩屑剥离岩石。通过对该过程的分析可发现，复合冲击作用加速了径向剪切裂纹、侧向裂纹和侧向主裂纹等宏观裂纹的产生，使岩石发生预损伤，有利于破岩效率的进一步提升。

3 复合冲击破岩影响因素及效应分析

PDC 钻头设计的不合理常导致钻齿崩裂等问题的产生，建立钻齿的切削力学模型是PDC 钻头进行合理设计的前提和基础。当前，钻齿切削力学模型主要围绕两方面来研究：一方面，通过分析钻齿的接触弧长、切削面积和岩石的参数等，建立钻齿和各变量之间的回归关系，从而得到钻齿侵入切削破岩的经验模型，但该模型无法揭示钻进过程中的破岩机理；另一方面，结合室内实验和数值模拟，建立单钻齿侵入切削破岩力学模型，并进一步开展验证，该过程可以同步分析钻齿破岩机理。本文采用连续-非连续介质力学方法，通过建立单钻齿的破岩力学模型，研究岩石在复合冲击作用下从连续介质到非连续介质的损伤演化过程。

3.1 切削深度

钻进参数及钻齿的尺寸会影响钻齿切入岩层的深度，进而影响钻齿切削时的受力状态。本节基于所建立的复合冲击单齿侵入破岩数值模型，分析复合冲击作用下钻齿切入深度和切削力的关系。在保持其他参数固定不变的前提下，将钻齿的切削深度分别设置为2、3、4、5、6、7 mm，在对结果的分析过程中，建立了钻齿和切削力的相互作用关系，并通过分析岩石的破碎体积来评价破岩效率。

图17 为钻齿在不同切入深度下的破岩效果图。通过对该过程分析发现，当钻齿吃入岩层的深度较浅时，钻齿与岩层的接触面积和接触弧长较小，钻齿的冲击做功几乎全部用来粉碎表面的岩层。此时，在钻齿的前方和下方产生的岩石碎屑均较小，岩石的破碎体积也较小，在图17a 中效果较为明显。随着钻齿吃入岩层深度的增大，钻齿与岩层的接触面积也相应增大，岩石的破碎体积增大，图17e 和图17f 效果较为明显。钻齿的冲击做功一部分用于破碎岩层表面岩石，另一部分则对岩层内部产生损伤，加速裂纹向岩层内部的延伸和扩展，如图17c 和图17d 所示。当钻齿切入岩层的深度更进一步加深时，钻齿与岩层的接触面积变大，岩层的破坏区域变大，易产生较大的岩屑，但难以进一步对岩层产生破坏，如图17e 和图17f 中所示。

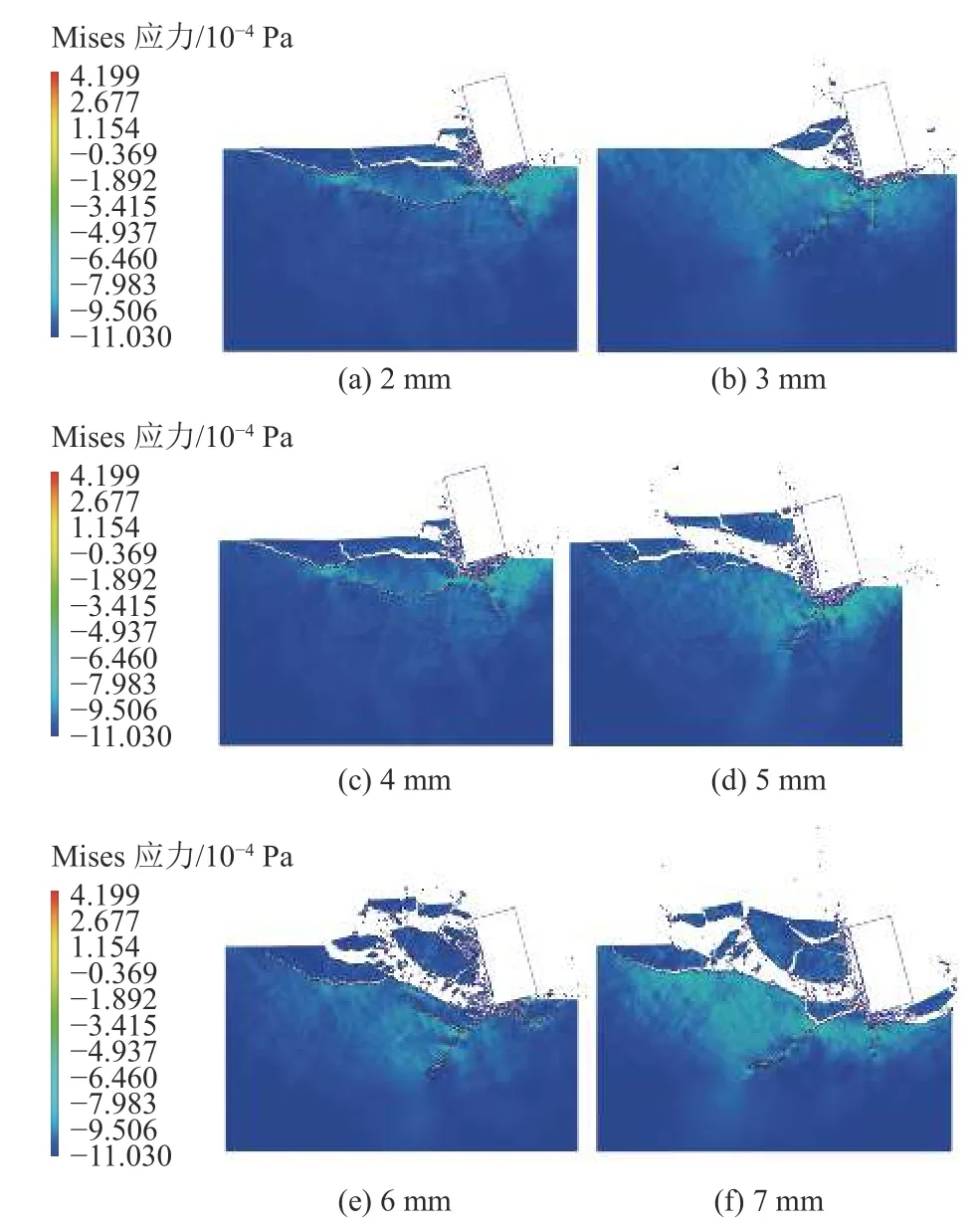
图17 切削深度与破岩效果Fig.17 Penetration depth and rock breaking effect

钻齿的切削力随着切削深度的增加而增加，同等条件下使钻齿保持较小的切入深度可提高钻齿的使用寿命。但是，通过对图17 的作用过程可发现，较小的切入深度会使岩层表面的岩石破碎范围较小，同时产生更小的岩屑，难以对深处岩层产生进一步的破坏。因此，为合理利用能量，提高破岩的效率，将进一步通过岩石的破碎体积来评价破岩效果。

在数值分析的基础上分别监测了不同切入深度下岩石的破碎体积，如图18 所示，钻齿受到的切削力在2～6 mm 切入深度范围内总体呈现上升趋势。这是由于当钻齿的切入深度较小时，钻齿与岩层的接触面积较小，钻齿对岩层的破坏范围也较小，此时钻齿的冲击做功主要用于破碎小范围的岩石，难以对岩层产生深入破坏。随着钻齿吃入岩层深度的增加，钻齿与岩层间的接触面积增大，钻齿对岩层的破坏范围变大。钻齿的冲击做功可用于破碎表面岩层和加速裂纹向岩层内部的延伸扩展，此时产生的岩屑较多，且可观察到裂纹向岩石内部扩展，为下一步破岩创造条件。而当钻齿吃入岩层的深度继续增大时，钻齿的冲击做功则难以破碎岩层的表面，只能使岩层产生大范围的损伤，同时钻齿所受的切削力也较大，此种条件下也易发生钻齿的崩坏现象。

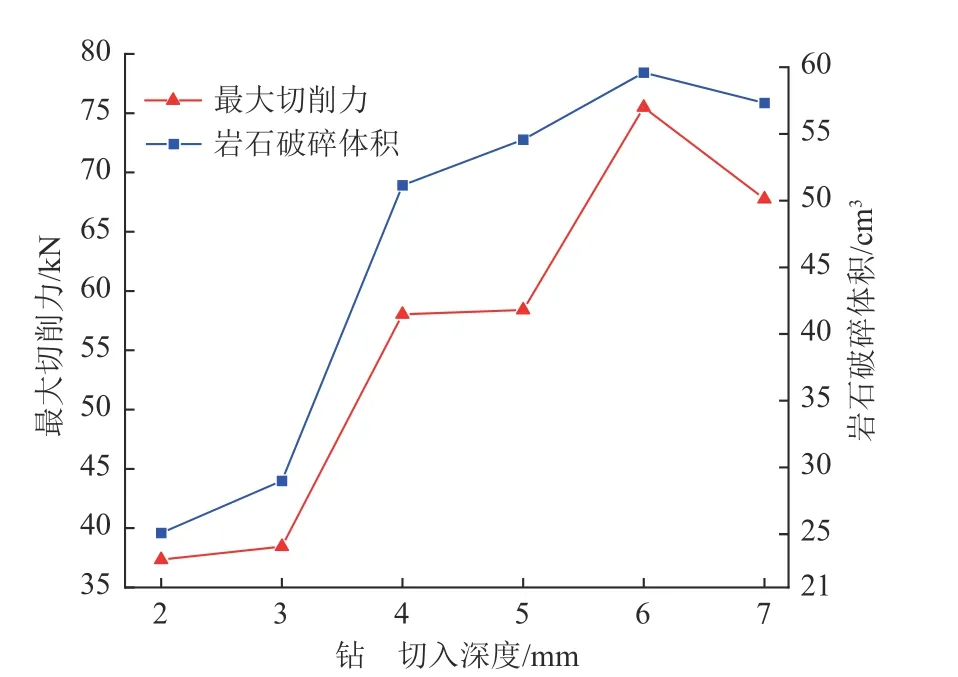
图18 切削深度-最大切削力、岩石破碎体积关系Fig.18 Relationship of penetration depth,maximum penetrating force and rock breaking volume

通过分析钻齿的切削力和岩石的破碎体积发现，若要保证良好的破岩效果，可选择切入深度为6 mm。此时钻齿的破岩效果最好，相应地，钻齿的切削力也最大，在钻齿设计时需综合考虑钻齿的强度参数。

3.2 钻齿前倾角度

钻齿的前倾角度是影响冲击能量在水平和垂直方向分布的重要参数，本节分析了钻齿前倾角和破岩效率的关系。在保持其他因素不变的前提下，设定钻齿的前倾角度分别为10°、15°、20°、25°、30°、35°。通过对数值模拟结果和数据的分析，建立钻齿前倾角和切削力的关系，并结合岩石的破碎体积来确定钻齿的最优冲击前倾角度。

图19 为不同倾斜角度下的破岩效果。通过分析该过程发现，钻齿的前倾角度影响了轴向冲击和扭转冲的能量分布，当钻齿的前倾角度较小时，钻齿前方岩石的破碎体积较小，且岩层内部的裂纹发展速度较慢，图19a 和图19b 效果比较明显。随着钻齿前倾角度的增大，钻齿前方的岩石破碎体积变大，且产生体积较大的岩屑，同时裂纹逐渐增多，有向岩石内部延伸扩展的趋势，图19e 和图19f 效果较明显。

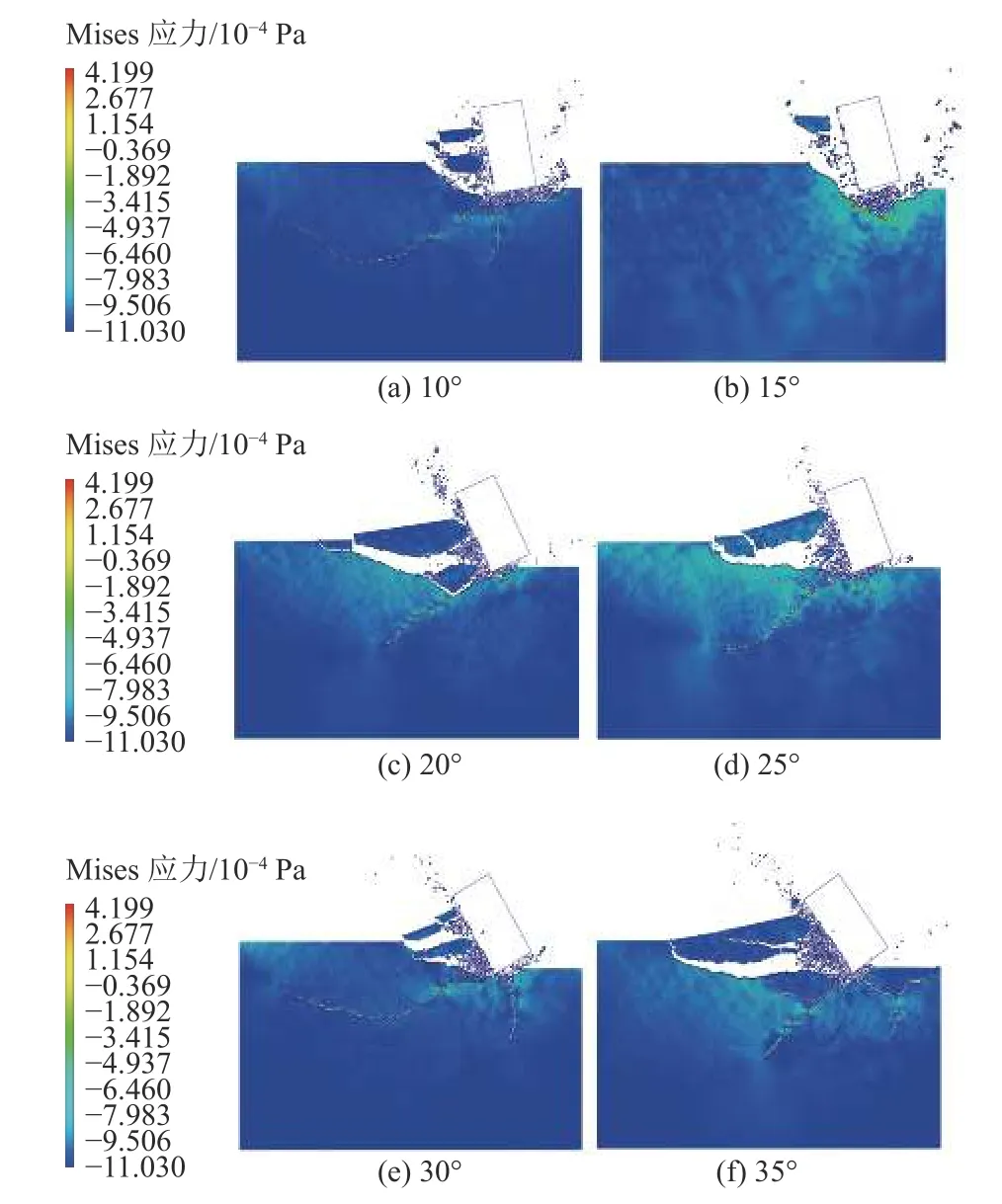
图19 钻齿倾角与破岩效果Fig.19 Rake angle of drill bit and rock breaking effect

钻齿切削力及破岩体积如图20 所示，通过数据分析可发现，随着钻齿前倾角的增大，钻齿所受到的切削力呈现先减小后增大的趋势。当钻齿的前倾角在10°～30°范围内时，其所受的切削力呈现下降趋势，且下降的幅度较大。在30°～35°范围内时，切削力呈现增大的趋势，当钻齿的前倾角度为30°时，钻齿的切削力取得最小值。随着前倾角的增大，钻齿前方的岩石损伤破坏面积先减小后增大，当钻齿的前倾角度较大时，岩石产生的裂纹逐渐向内部延伸和扩展，产生较大的岩石碎屑。这是由于随着钻齿前倾角度的增大，作用在水平方向上的冲击能量随之增大，作用于垂直方向上的冲击能量逐渐减小，通过图19 也可发现，随着前倾角的增大，宏观裂纹的数量也逐渐增加，说明轴向冲击作用对宏观裂纹的发育影响较大。

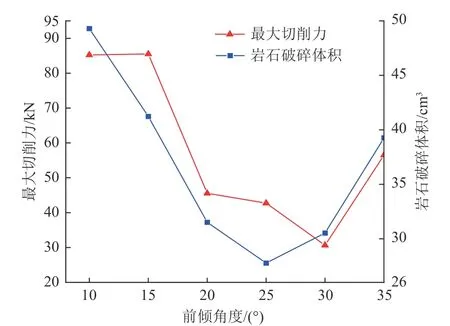
图20 前倾角度-切削力、岩石破碎体积曲线Fig.20 Relationship of rake angle,penetrating force and rock breaking volume

通过分析不同前倾角度下的破岩体积发现，岩石破碎体积在前倾角10°～25°时呈下降趋势，在25°～35°呈现上升趋势。同时结合钻齿在破岩时所受到的最大切削力发现，当钻齿前倾角在30°左右时，钻齿所受的切削力最小，此时将有效保护钻齿，防止发生崩齿现象。若要综合考虑破岩效果，可选择较小的破岩效果，如选取前倾角10°～15°，此时岩石的破碎体积较大，破岩效率较高。

3.3 轴向冲击速度幅值

冲击速度幅值的增大会增加钻齿单次冲击的能量，在保持其他参数不变的前提条件下，研究轴向冲击速度幅值对破岩效率的影响，分析不同轴冲速度幅值下的破岩规律。分别选取轴向冲击速度的幅值为0.2、0.4、0.6、0.8、1.0、1.2 m/s。

图21 为不同轴向冲击速度对破岩效果的影响。随着钻齿轴向冲击速度的增大，钻齿下方岩石的破碎体积逐渐增大。在较大的轴向冲击速度下，钻齿下方的岩石更易产生侧向裂纹，轴向冲击速度的增大加速了宏观裂纹的萌生和扩展，更容易使岩石发生破坏。

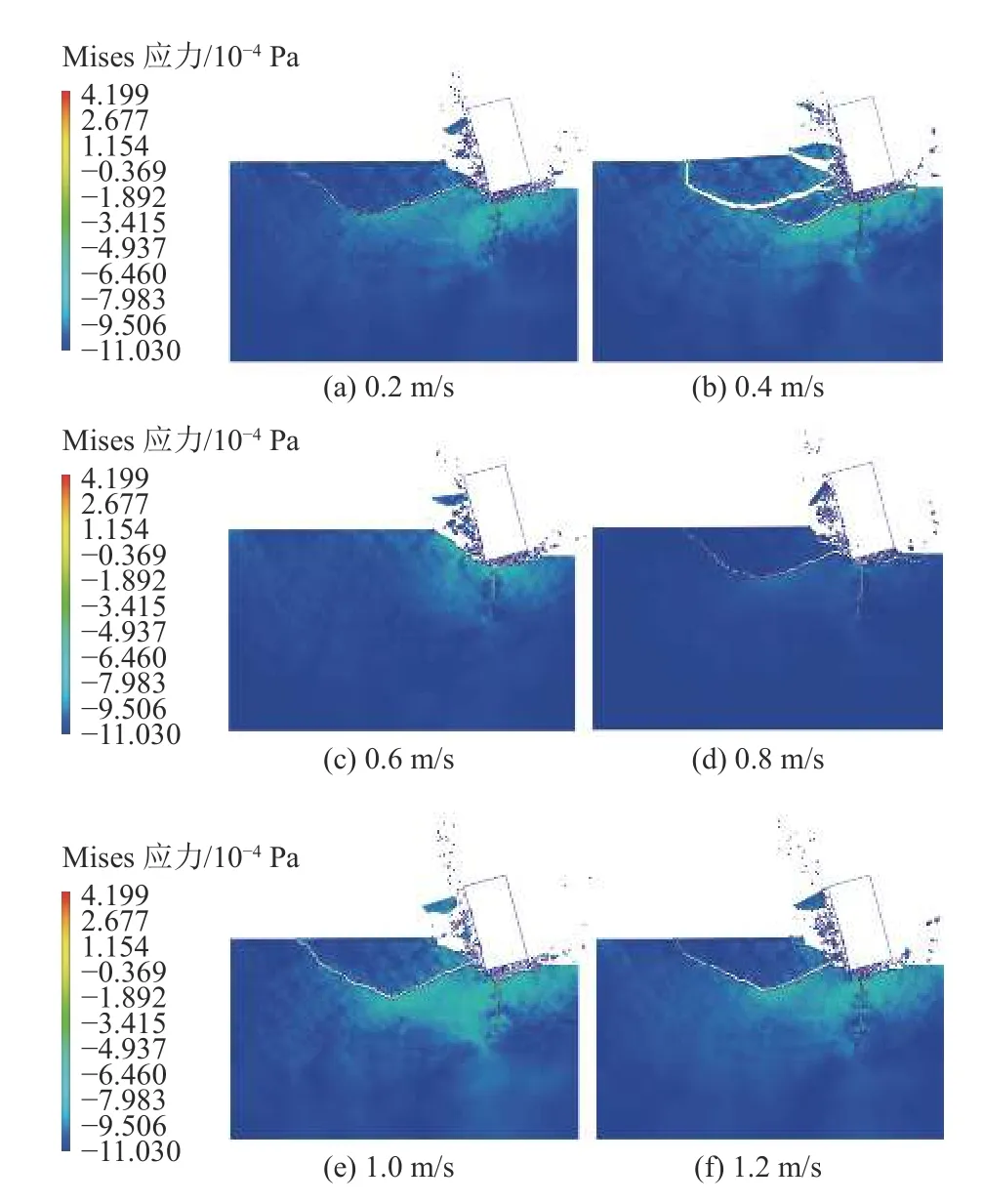
图21 轴向冲击速度与破岩效果Fig.21 Axial impact velocity and rock breaking effect

当钻齿的轴向冲击速度较小时，钻齿在轴向吃入岩层的深度就会变小，此时配合扭转冲击速度可使岩层表面发生小范围破坏。随着钻齿冲击速度的增大，岩层在冲击作用下会迅速出现损伤演化，岩层内部也会进一步产生裂纹。

图22 为不同轴向冲击速度幅值下钻齿切削力及破岩体积变化的关系，随着轴向冲击速度的增加，岩石的破碎体积呈现增大的趋势，当冲击速度幅值位于0.8～1.0 m/s 时，岩石破碎体积增加的速度最大。轴向冲击速度的增大更利于岩石的损伤演化，轴向冲击速度幅值越大，岩石体积的破碎范围就越大。钻齿所受到的最大切削力在0.2～0.6 m/s 和0.8～1.2 m/s 范围内增大，在0.6～0.8 m/s 范围内减小。当钻齿的轴向冲击速度幅值取得0.8 m/s 时，钻齿所受的切削力最小。同时，分析岩石破碎体积曲线可知，随着轴向冲击速度的增加，岩石破碎体积也不断增大，选择较大的轴向冲击速度有利于提高破岩效率。同时结合钻齿所受到的最大切削力，当钻齿的轴向冲击速度幅值为0.8 m/s 时，钻齿可得到有效的保护。

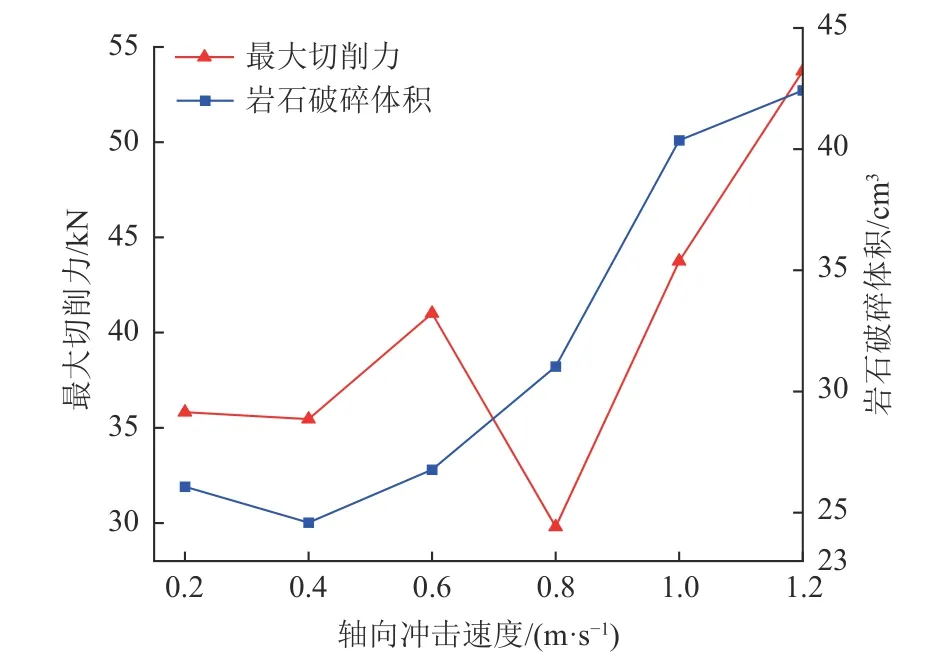
图22 轴向冲击速度-最大切削力、岩石破碎体积曲线Fig.22 Relationship of axial impact velocity,maximum penetrating force and rock breaking volume

3.4 扭转冲击速度幅值

在保持其他参数不变的前提条件下，进一步分析扭转冲击速度幅值的切削作用对破岩效率的影响，分别选取扭转冲击速度的幅值为0.1、0.2、0.3、0.4、0.5、0.6 m/s。通过对数值模拟结果和数据的对比研究，分析不同扭转冲击速度下的破岩规律，建立扭转冲击速度幅值和切削力的关系，并结合岩石破碎体积，确定了钻齿的最优冲击速度参数。

图23 为不同扭转冲击速度对破岩效果的影响。当扭转冲击速度的幅值较小时，钻齿前方和下方的岩石破碎范围较小，岩石产生的碎屑也较小。随着冲击速度幅值的增大，钻齿对岩石的破碎范围增大，岩石内部产生较多的宏观裂纹。这是由于当钻齿的冲击速度较小时，钻齿积蓄的能量较小，难以对钻齿前方和下方的岩石产生进一步破碎。冲击速度幅值的增大加速了宏观裂纹的产生和扩展。

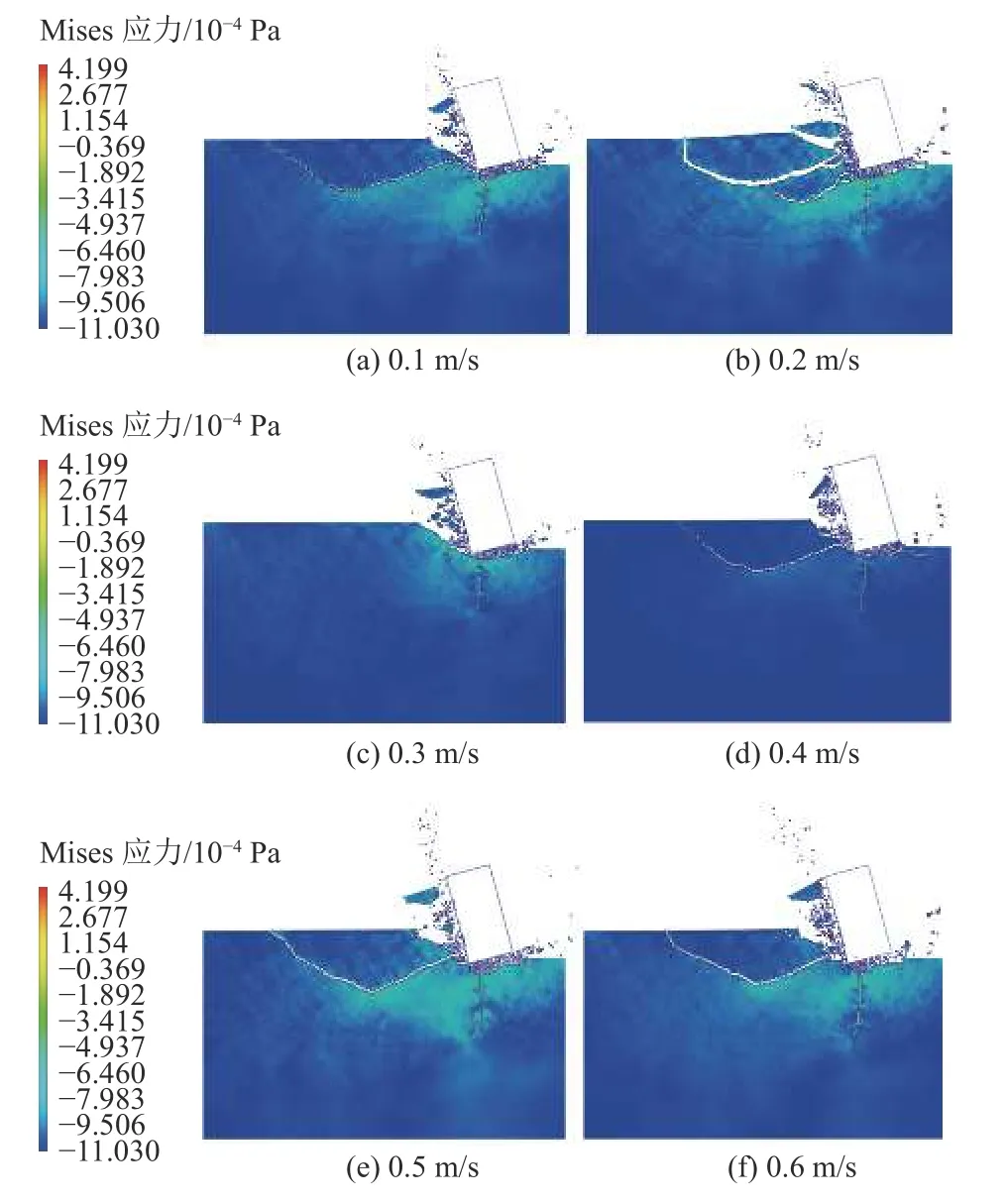
图23 扭转冲击速度与破岩效果Fig.23 Torsional impact velocity and rock breaking effect

当钻齿的扭转冲击速度幅值较小时，钻齿积蓄的能量较小，钻齿难以进一步切削岩层，此时钻齿仅能对小范围内的岩层产生破坏，易产生较小的岩屑。随着扭转冲击速度幅值的增大，钻齿的切削能力增大，岩层在冲击作用下产生密实核和破碎区，岩层的内部也将会出现损伤破坏，同时出现宏观裂纹的扩展现象，此时能量利用率较高，能够达到较好的破岩效果。

图24 为钻齿扭转冲击速度幅值和破碎体积关系曲线，曲线整体呈现先增大后减小的趋势。在初始阶段，岩石的破碎体积较小，随着扭转冲击速度幅值的增加，岩石破碎体积逐渐增大，当扭转冲击速度幅值达到0.3 m/s 时，岩石破碎体积达到最大，同时钻齿所受到的切削力也较小。从破岩效率和钻齿寿命两方面来综合考虑，当扭转冲击速度为0.3 m/s 时，钻齿的寿命可得到有效延长，且此时岩石的破碎体积较大，具有良好的破岩效果。

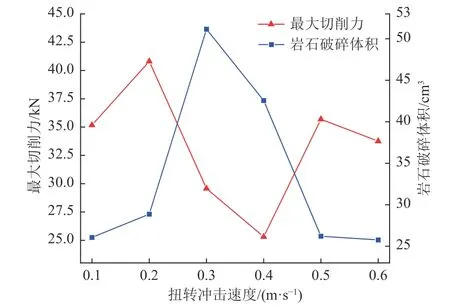
图24 扭转冲击速度-最大切削力、岩石破碎体积曲线Fig.24 Relationship of torsional impact velocity,maximum penetrating force and rock breaking volume

4 结论

a.基于连续-非连续分析方法，建立了基于共享节点的FEM-DEM 耦合岩石模型，该模型可将有限元与离散元优势有机结合，实现岩石材料从连续介质到非连续介质的过渡。开展了室内单轴压缩实验，从岩石试件破坏现象及应力-应变曲线关系方面证明了该岩石本构模型的合理性。在此基础上，通过JavaScript二次开发，建立了适用于分析复合冲击破岩钻进的连续-非连续数值计算模型，可为钻齿参数的优化设计提供一定的借鉴。

b.复合冲击作用是一个能量积累和释放的过程，在复合冲击作用下，钻齿的前方和下方岩石均发生大体积破碎，相较于单维度的轴向冲击或扭转冲击，复合冲击可实现“立体破岩”效果，减小钻头的粘滑效应。同时，复合冲击作用加速了径向剪切裂纹、侧向裂纹和侧向主裂纹等宏观裂纹的产生，使岩石发生预损伤，更利于破岩效率的进一步提升。

c.钻齿的切入深度、冲击角度、轴向冲击速度幅值、扭转冲击速度幅值是影响复合冲击破岩效果的关键因素。钻齿的破岩效果随着切入深度的增大逐渐呈增长趋势，钻齿切入深度为6 mm 时，钻齿的破岩效果最好，但钻齿所受的切削力也最大；冲击角度影响了冲击能量在水平和垂直方向分布，较小的前倾角度下可实现较好的破岩效果，如前倾角在10°～15°时破岩效率较高；选择较大的轴向冲击速度有利于提高破岩效率，当钻齿的轴向冲击速度幅值为0.8 m/s 时，钻齿破岩效果较好，且钻齿可得到有效的保护；当扭转冲击速度为0.3 m/s 时，钻齿的寿命可得到有效延长，且此时岩石的破碎体积较大，具有良好的破岩效果。

d.钻头复合冲击破岩是一个动力学和静力学耦合的复杂过程。本文仅围绕复合冲击作用下的单钻齿侵入破岩规律开展了具体研究，而在岩石的破碎能耗规律方面涉及较少。建议在后续研究中，可围绕岩石塑性耗能和脆性耗能情况、动静态荷载作用下岩石的应力场演化规律、岩石的破碎比能耗关系等方面开展针对性研究。同时，开展多种地质情况下的现场实验，建立不同钻进参数、不同地层参数的关系，以便更好地指导实际施工。