网格加筋结构集中力扩散肋的传力机理研究

王卓群，郝 鹏，王 禹，王桂娇，刘力源

（1.北京宇航系统工程研究所，北京，100076；2.大连理工大学，大连，116081）

0 引言

航天箭体部段间的连接构件，除连接功能外，其最主要的目的是将一侧较大的集中力均匀扩散到另外一侧。贮箱短壳上以多点集中载荷为主，结构设计过程需要考虑集中力扩散效应。因此，该类航天薄壳设计中大量使用了扩散肋结构形式，即短壳蒙皮上从集中力处开始的筋条采用的是直条形放射状。这类结构形式起到了传递和扩散高应力局部集中力的作用，有效避免了局部强度破坏，并使得更多蒙皮材料参与承载。在大幅提升材料利用效率的同时，也为箭体结构创造了良好的受力环境。但传统的扩散肋形式往往采取保守设计，易导致结构超重［1-2］。为了提升火箭结构设计的精细化程度，更好发挥扩散肋作用，需要对其传力原理及结构设计方法进行深入探究。

在网格加筋结构设计中，有2 个重要的设计参数：筋条布局和筋条截面尺寸。对于薄壳结构，无论壳体承受何种形式的外载，壳体的内力形式总能分为两类：第一类是面内拉伸、压缩、剪切；第二类是面外弯曲。面内的力决定了筋条的最优分布，面内和面外的力同时决定筋条截面的最佳尺寸。因此，本文从筋条布局设计和筋条截面设计两个角度出发：首先探究筋条及扩散肋结构的传力原理。然后，基于传力原理和等几何分析提出了一种集中力扩散加筋模型的高效结构设计方法。最后，通过平板和曲壳的算例验证了本方法的有效性。

1 扩散肋传力机理研究

贮箱短壳承受多点集中力载荷，结构上通常需要采取图1所示的集中力扩散措施［3］。当前结构设计中，使用扩散肋首先要避免集中力作用区域发生应力集中破坏，抑制最大应力，将应力向周围扩散，利用更多的材料抵抗载荷；其次要将集中力均匀扩散，网格加筋结构整体刚度很高，然而对抗集中载荷的能力较弱，因此短壳承受集中载荷后，希望力传到另外一侧时的支反力趋近均匀分布，有利于对相邻结构的承载。

图1 航天装备中扩散肋结构示意Fig.1 Sketch of radial ribs in aerospace structures

在寻求布局最优的结构优化设计中拓扑优化应用广泛，其基本思想是寻求结构单元的密度，将材料最优分布问题转化为单调函数的连续变量的优化问题［4］，对探究筋条传力可以起到指导性作用。

筋条可视为杆或梁结构，对于杆或者梁结构的布局优化设计，1904 年Michell［5］解析推导了桁架结构设计理论，推导的解析最优形式与该设计领域的主应力线十分吻合。在设计域内确定了足够多的主应力平面后，主应力线可以通过连接这些主应力平面进而获得主应力场。如图2所示，设计域内的主应力场提供了自然的传力路径可视化方案，材料的几何分布形式是朝着主应力线的方向逐渐收敛的，既不受材料刚度变化的影响，也不受施加的力的重新缩放的影响，而受设计域载荷、约束及结构几何形状等属性的影响。由此可知，结构主应力分析获得的主应力场中蕴含着结构几何的最佳拓扑，筋条最优布局应符合设计域的主应力场分布。

图2 Michell桁架解析解、拓扑优化设计、结构主应力场三者之间横向对比Fig.2 Comparison among analytical expression of Michell truss,topology optimization and structural principal stress field

在扩散肋结构截面尺寸设计方面，可用如图3所示的矩形水平梁来简要说明截面尺寸对传力的影响。

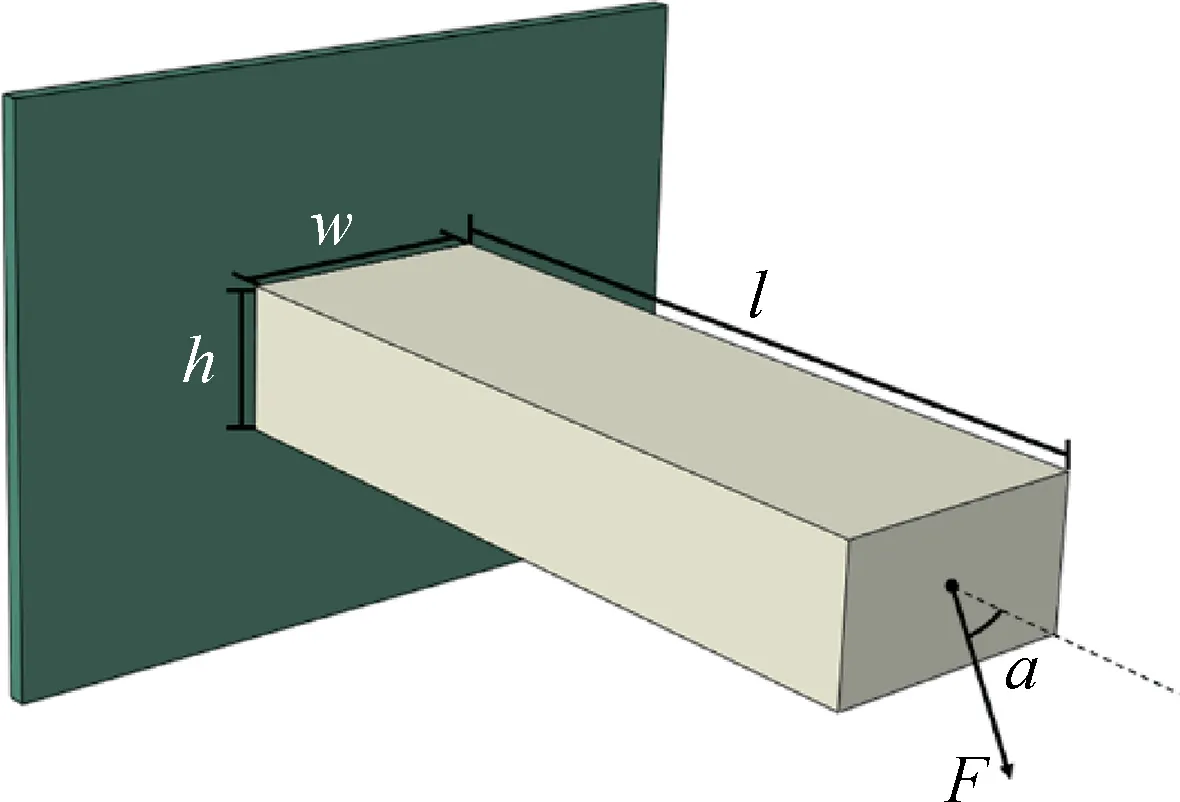
图3 水平梁模型Fig.3 Longitudinal beam model

考虑单一水平梁模型的优化问题，如图3 所示，水平梁左侧固定，右侧受载，当任意截面处的极限应力是一个定值时，沿着梁的力与截面面积wh成正比，垂直于梁的力与梁截面惯性矩wh3/12成正比，即在材料不发生破坏的前提下，提升梁的高度h对于提升结构承载能力来说是性价比最高的选择。当筋条截面应力为常数时，筋条传递的力与截面面积成正比。因此对扩散肋结构，不同的筋条截面面积决定了筋条的刚度，为了使得扩散肋传递过去的支反力能够更加均匀，就需要利用截面尺寸进行刚度调控。

本节对扩散肋力学性能起到关键作用的筋条布局和筋条截面尺寸的传力机理进行了探究。筋条布局的基本构型应当符合壳体表面的主应力迹线，筋条截面尺寸则与固支端支反力的分布直接相关。

2 基于扩散肋传力机理的网格加筋薄壁结构设计方法

基于扩散肋（筋条）的传力原理，本文建立了网格加筋薄壁结构的快速设计方法，并基于该设计方法对平板和短壳算例进行设计，验证了设计方法的有效性和正确性。整体设计框架如图4所示。

图4 基于扩散肋传力原理的薄壁网格加筋结构设计方法Fig.4 Design method of radial ribs for thin-walled grid-stiffened structures

本文方法分为筋条布局设计和筋条截面设计2个主要步骤，为了保障设计过程中数值分析的精度和效率，本文采用等几何分析对曲面结构和加筋结构进行静力工况分析。

2.1 加筋薄壁结构等几何分析

等几何分析是一种高阶有限元分析方法，它基于经典有限元算法中的等参思想，直接利用CAD 的几何模型作为CAE 中的分析模型，将用来描述几何模型的样条基函数用作分析中的插值函数［6-7］。加筋结构的等几何分析能够为加筋设计提供高效的分析方法，且使得加筋设计与CAD系统实现无缝集成。

等几何分析的重要基础是非均匀有理B 样条（Nonuniform Rational B-spline，NURBS）曲线和曲面，一条p次NURBS曲线定义为

式中Pi为NURBS 曲线控制点（它们形成控制多边形）；Ri，p(ξ)为NURBS 曲线有理基函数；n为NURBS曲线控制点的数量。

一个在ξ方向p次、η方向q次的NURBS曲面可定义为

式中Ni，p(ξ)和Nj，q(η)分别为p阶和q阶的一维向量空间的B 样条基函数；ωi，j是Ni，p(ξ)和Nj，q(η)对应的权函数。

在加筋结构的等几何分析中，加强筋与壳体之间的耦合不能通过简单的控制点匹配来处理。本文采用插值法解决加强筋与壳之间位移不相容问题，在加强筋控制点与壳控制点不匹配的情况下，保证计算精度仍然较高。如图5所示该方法的主要过程是将加强筋控制点投影到壳上并求出投影点的壳参数域坐标，然后利用壳体控制点的位移求解加强筋控制点的位移，最后得到位移转换矩阵。

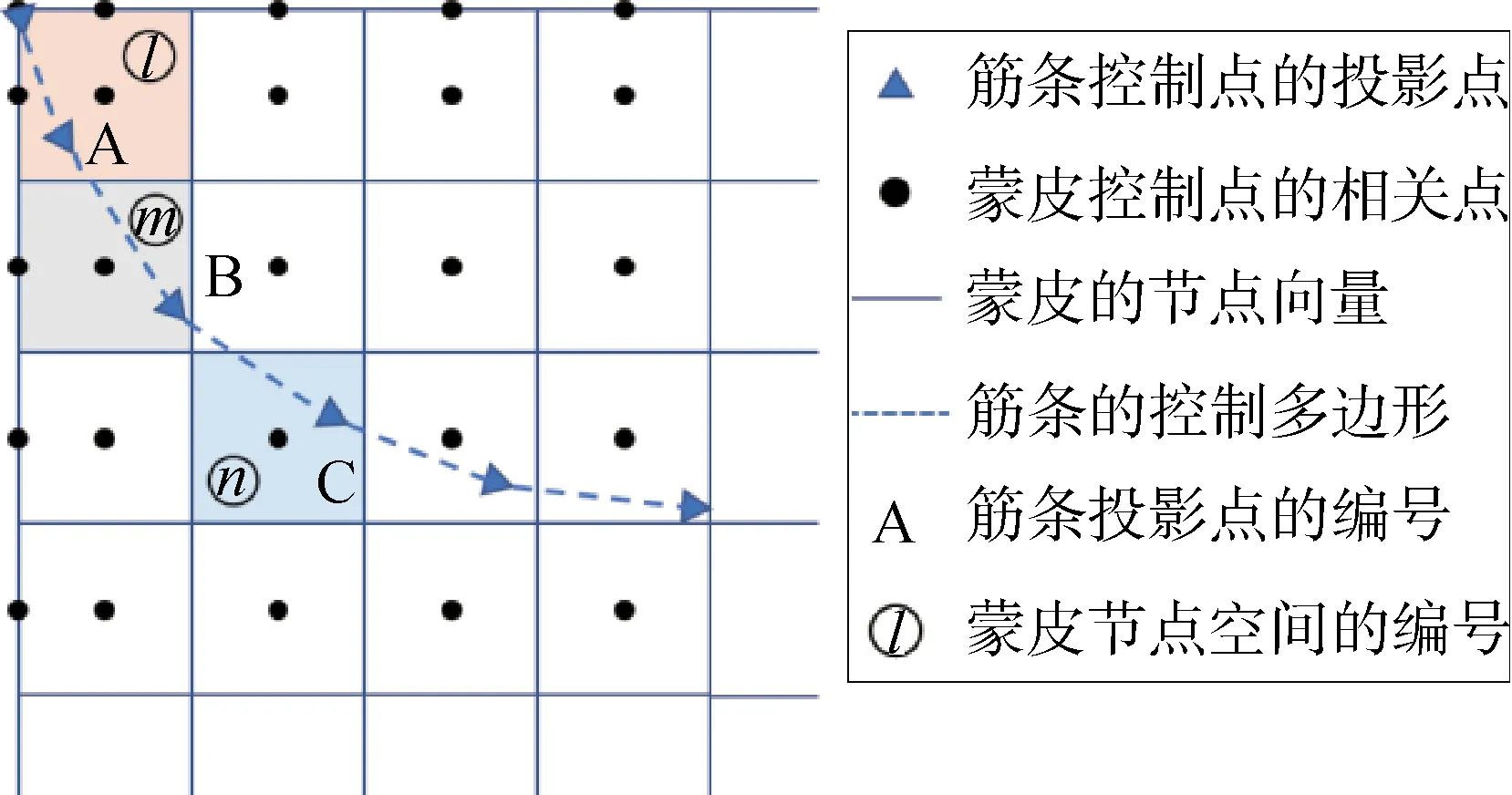
图5 壳单元内的加强筋单元Fig.5 Stiffener elements within shells

下面以二阶NURBS 基函数为例推导具体公式。NURBS曲面（壳）与NURBS曲线（加强筋）的关系如图5 所示。一个加强筋单元的控制点是A、B 和C。对应的参数坐标为(ξA，ηA)，(ξB，ηB)和(ξC，ηC)。对应的节点跨度为l、m和n。加强筋控制点的位移可以表示为如下插值形式：

式中δs为加强筋一个单元的位移集合；δ为与加强筋相关的蒙皮上控制点的位移。利用式（5）的变换关系，可以将加强筋的刚度和几何刚度矩阵组装到板中：

对于静态分析，控制方程为

式中K为蒙皮刚度矩阵；U为位移向量；F为载荷向量。

可以发现，最终组装的刚度矩阵的规模与壳的刚度矩阵规模相同，这相当于消除了加强筋单元的自由度。这意味着计算规模大大缩小，且可以适应更多的加强筋形式。具体推导过程详见文献［8］。

2.1.1 基于传力机理的筋条布局设计方法

综上可知，扩散肋结构布局的传力机理为蒙皮结构的主应力方向。本节提出了一种基于传力机理的网格加筋布局设计方法，在给定了蒙皮曲面形状及边界条件后，该方法通过以下4 个步骤（如图6 所示）即可快速获取网格加筋结构的布局设计：a）基于等几何分析求解蒙皮结构在三维空间中的传力方向，即面内主应力方向；b）使用张量变换公式，将传力方向转换到曲面的二维参数域内；c）基于几何路径追踪算法，将传力方向拟合为传力路径NURBS 曲线；d）传力路径NURBS 曲线通过NURBS 基函数的仿射变换关系，从二维参数域映射到三维几何空间。设计流程全程使用基于NURBS 的几何模型，因此最终模型可直接导入CAD 软件中生成相应的实体几何模型。

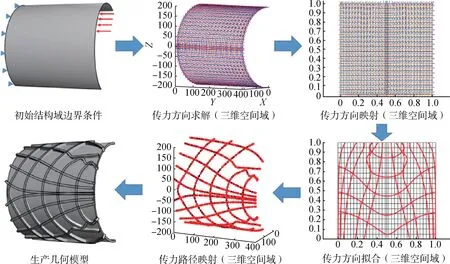
图6 基于传力机理的网格加筋结构布局设计方法Fig.6 Layout design of radial ribs for grid stiffened structures

2.1.2 基于刚度调控的筋条变截面设计

在第1节中讨论了筋条传递的力大小与截面面积之间存在正相关的关系。同时，在筋条布局设计过程中保证了筋条始终沿着曲面结构的主应力方向，因此，就保证了筋条截面承受的载荷是以拉力和压力为主的轴向载荷。在截面应力固定的情况下，筋条传递的力与筋条截面面积将成正比。若要保持扩散肋每根筋条传递的力是均匀的，在保持总体质量不变的情况下，通过结构参数优化来获得各筋条截面比例（如图7 所示），筋条截面呈非均匀分布，且两侧筋条截面面积大，越靠近中间，面积越小，因此需要对筋条进行变截面参数设计，以保证固支端支反力呈均匀载荷分布。

图7 筋条截面非均匀变高度参数化设计Fig.7 Parametric design of non-uniform and variable height rib sections

3 中力载荷下的加筋结构优化设计数值算例

随着火箭运载能力要求日益提高，对箭体结构系统精细化和可靠性设计需求愈发强烈，通过结构设计与仿真分析相结合等手段，对扩散肋进行精细化设计能够不断提高结构设计效率从而降低成本［9］。图8～9为典型贮箱短壳扩散肋局部结构，本文将通过算例结合仿真分析来验证所提出的结构设计方法的正确性。同时，为了验证结构设计的有效性，本文中所有设计结果均采用ABAQUS进行静力分析校核。

图8 非均匀截面扩散肋示意Fig.8 Design of non-uniform radial rib section

筋条与蒙皮的尺寸定义如图9所示。

图9 非均匀截面扩散肋示意Fig.9 Design of non-uniform radial rib section

3.1 矩形平板结构加筋补强设计算例

矩形模型板长为100 mm，宽为50 mm，厚度为2 mm，材料为2A14铝合金，弹性模量为68 646 MPa，泊松比为0.3，右侧中心四分之一区域承受2 500 N的载荷。

此载荷情况下，静力分析结果如图10所示。

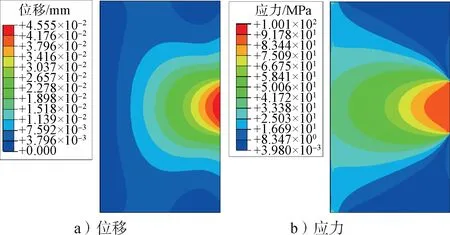
图10 静力分析结果Fig.10 Static analysis results of rectangular plate

根据静力分析结果，可以直接获取矩形板的主应力方向场，如图11所示。

图11 矩形板主应力场Fig.11 Principal stress field of rectangular plate

依据此主应力场，使用本文提出的基于传力机理的筋条布局设计方法，生成扩散肋加筋结构。本算例中主要讨论筋条截面对集中力扩散效果的影响，因此，不构造网格加筋，而是只沿着第一主应力方向构造扩散肋。扩散肋的形式如图12所示。

图12 含扩散肋的矩形板结构Fig.12 Rectangular plate with radial ribs

扩散肋截面为均匀截面，即所有的截面的宽度为1 mm，高度为4 mm，偏心度为0 mm。含扩散肋的加筋矩形板结构的静力分析位移和应力云图如图13所示。

图13 含扩散肋的加筋矩形板结构的静力分析结果Fig.13 Static analysis results of rectangular plate with radial ribs

与初始矩形板的位移和应力云图相比，可以发现应力集中现象得到了明显的改善，排除应力奇异点的影响，从图13b中可以明显观察到，初始结构中的大面积高应力区域已经消失。图14 为由固支端提取出的支反力绘制的折线图，其中节点的选取规则是沿着固支端均匀选取。在固支边界的支反力中明显观察到集中载荷还未得到有效扩散。因此保持所有筋条高度不变，通过优化设计宽度来调节筋条截面面积从而使支反力分布更为均匀。

图14 矩形平板算例固支边界支反力Fig.14 Reaction force of fixed boundaries

保持总体质量不变的情况下，通过变截面参数优化，可获得图15 所示的筋条截面比例，筋条截面呈非均匀分布，且两侧筋条截面面积大，越靠近中间，面积越小。

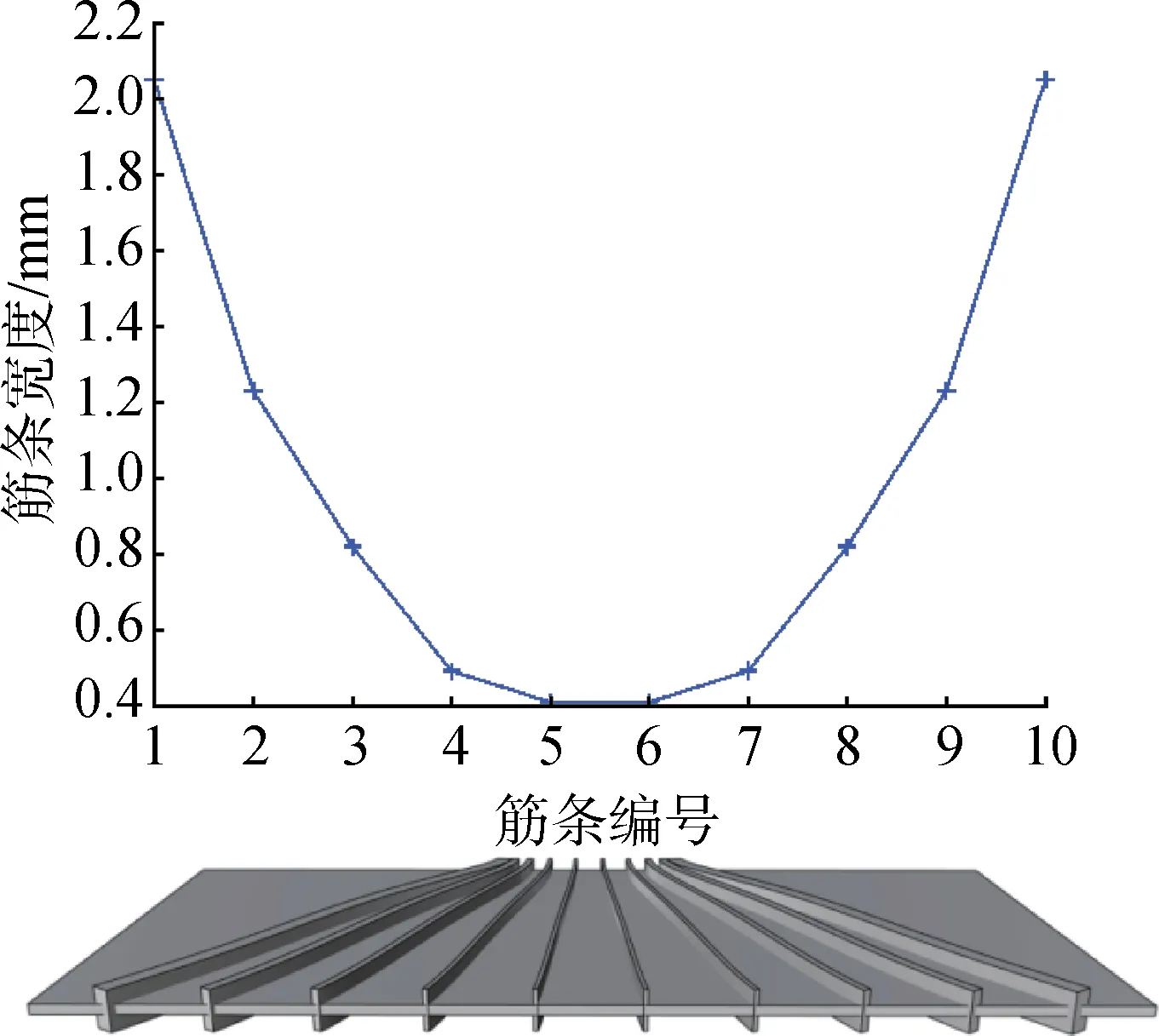
图15 非均匀截面扩散肋Fig.15 Non-uniform radial rib section

扩散肋优化为非均匀截面后，固支端的支反力为图16 中红色圆形折线，与均匀截面扩散肋的结果对比，可以明显发现，非均匀截面扩散肋的支反力呈均匀分布，说明集中力得到了有效的扩散。

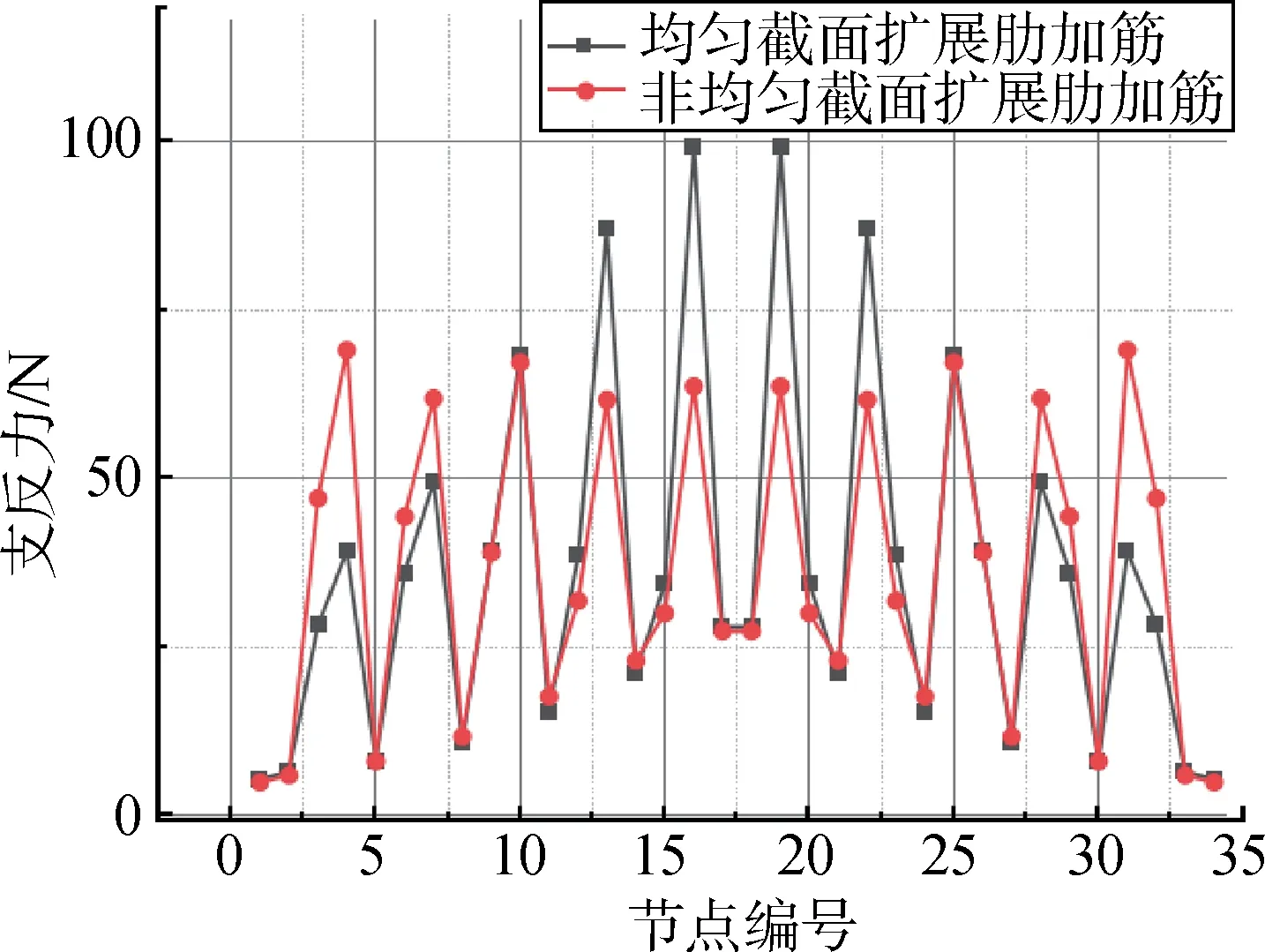
图16 均匀与非均匀截面扩散肋加筋结构固支端支反力对比Fig.16 Comparison of reaction forces of fixed boundaries between uniform and non-uniform rib sections

3.2 短壳结构加筋补强设计算例

以常用的短壳模型为研究对象，探究基于扩散肋传力机理的网格加筋薄壁结构设计方法在壳体中的适用程度。该模型尺寸为某型号二级燃箱后短壳的简化模型，直径为3 350 mm，高度为725 mm。模型整体承受8 个区域的集中载荷，8 个呈中心对称分布，单个加载区域的圆心角为10°，如图17所示。总载荷大小为22.4 t，蒙皮厚度为2 mm，材料为2A14铝合金，弹性模量为68 646 MPa，泊松比为0.3。本算例只考虑线弹性。

图17 模型及边界条件Fig.17 Boundary set of finite element model

短壳结构主应力场如图18所示。

图18 短壳结构主应力场Fig.18 Principal stress field of short shell

根据图18 的结构主应力场，以第一主应力场为主，构建扩散肋结构。基于等几何分析方法，筋条在模型八分之一参数域内的分布如图19所示。

图19 筋条在模型八分之一参数域内的分布情况Fig.19 The distribution of ribs in the eighth parameter domain of the model

将参数域内的筋条映射到空间曲面上，筋条的宽度为5 mm，高度为10 mm，偏心度为0 mm，含扩散肋的短壳模型如图20所示。

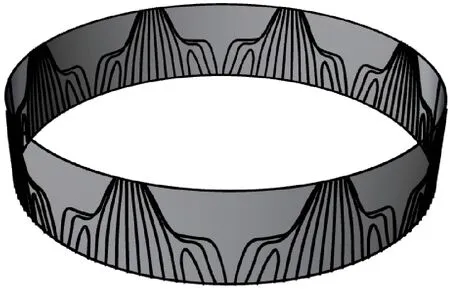
图20 含扩散肋的短壳模型Fig.20 Short shell model with radial ribs

对光壳模型和含扩散肋的短壳模型同时进行静力工况有限元分析，位移和应力云图如图21所示。

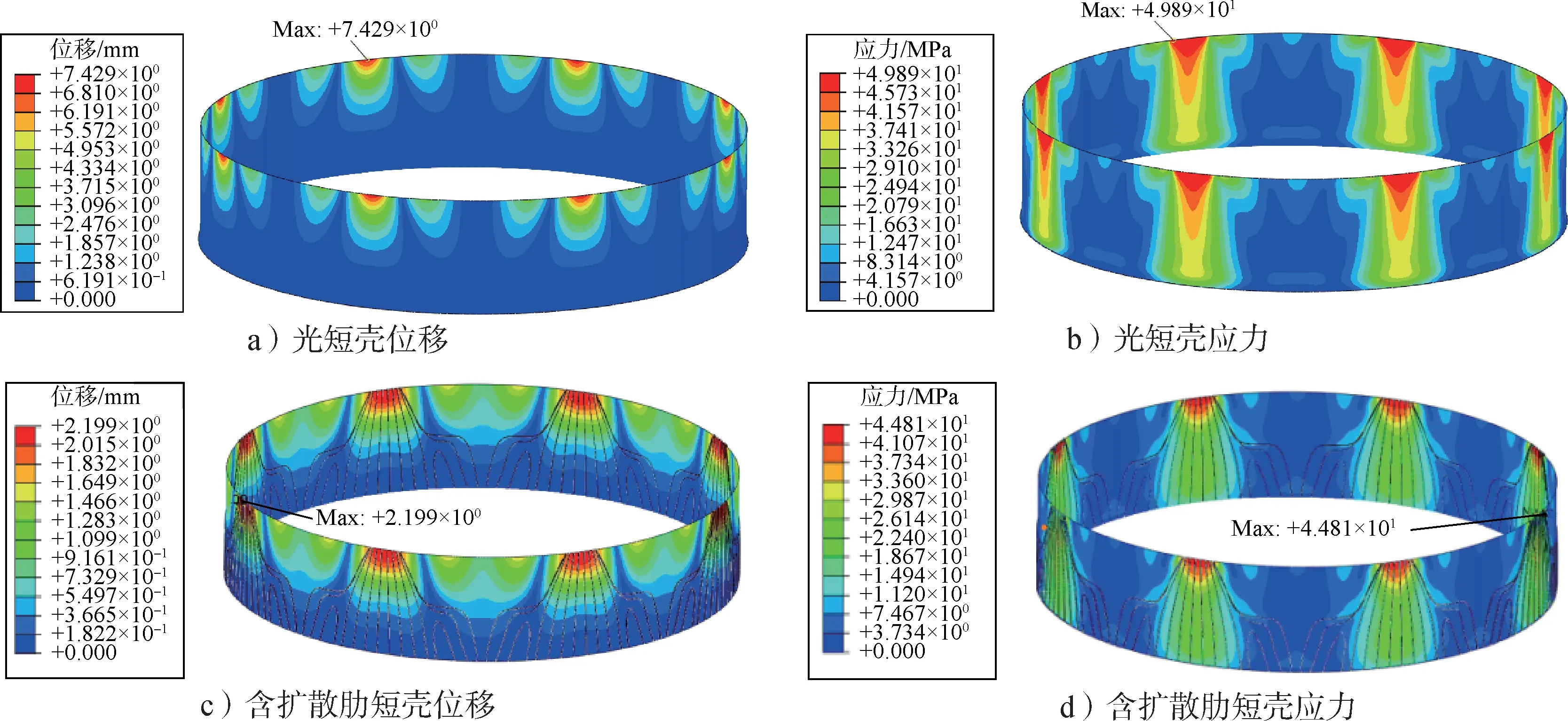
图21 短壳的位移及应力云图对比Fig.21 Comparison of displacement and stress of short shell

通过与光短壳的分析结果进行对比可以发现，扩散肋的引入，明显改善了应力和位移云图中由于集中载荷引起的高位移和高应力。最大位移降低了70%，最大应力没有改变，但是由应力云图可以发现，最大应力区域面积明显降低。

扩散肋固支边的支反力如图22 所示，支反力呈现出集中载荷分布情况，说明顶部集中载荷并未被完全扩散。

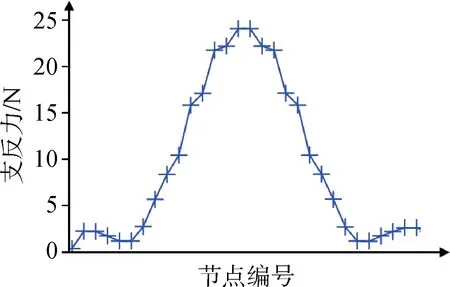
图22 均匀截面扩散肋八分之一短壳固支端的支反力Fig.22 The support reaction force of an 1/8 short shell with uniform cross-section and diffusion ribs at the fixed end

在基于传力路径的设计中，每根筋条传递的力与截面面积是成正比的，为了保证支反力更为均匀，截面面积需要与筋条主应力的值成反比。在保持总体质量不变的情况下，对筋条截面进行优化，优化后的非均匀截面如图23所示。

图23 非均匀截面分布Fig.23 Section layout of non-uniform ribs

使用非均匀截面后，短壳结构固支端的支反力如图24 所示，可以发现图22 中支反力集中部分被有效消除，图24 中的支反力分布更加均匀，因此通过对截面的优化可以明显改善短壳固支端的支反力。

图24 非均匀截面扩散肋八分之一短壳固支端的支反力Fig.24 The support reaction force of an 1/8 short shell with nonuniform cross-section and diffusion ribs at the fixed end

3.3 集中力载荷下含开口的网格加筋二级燃箱后短壳算例

结构开口导致的刚度分配不均，同样会引起类似于集中载荷的效果，因此扩散肋形式的网格加筋对开口具有补强作用。由于开口数量、形状等不确定因素，导致筋条场的分布变得更加复杂。对含开口的贮箱后短壳结构中的扩散肋重新进行设计，初始模型如图25a 所示。分析集中力载荷下结构应力应变水平，并与未优化初始的短壳模型作对比。使用本文提出的方法设计的含开口后短壳结构如图25b所示，其扩散肋结构分布及筋条尺寸如图26 所示，其中筋条宽度呈对称分布。

图25 优化前后含开口的网格加筋贮箱短壳模型对比Fig.25 Regular short shell in comparison to optimized model

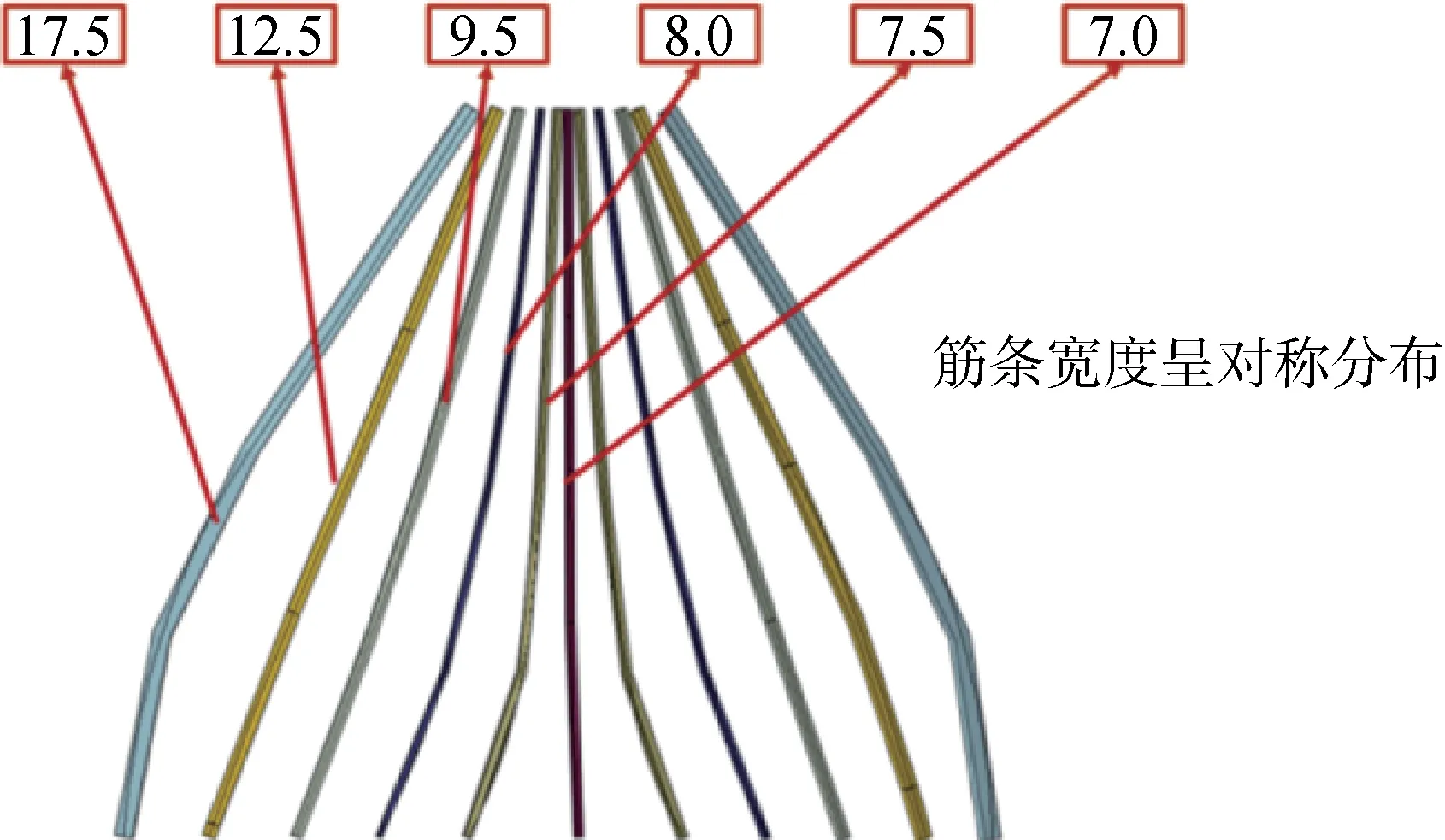
图26 基于传力路径的扩散肋结构尺寸（单位：mm）Fig.26 Width distribution of radial ribs based on force transfer path

上边界集中力的总载荷为126.96 kN，提取基于传力机理设计的加筋结构和初始模型的位移和应力结果如图27和图28所示，相对于初始模型，后短壳位移显著减小，并且位移分布更为均匀，最大位移减小29.6%。

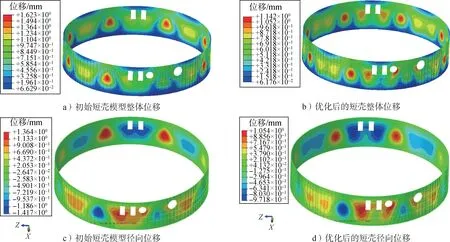
图27 含开口加筋短壳优化前后位移对比Fig.27 Comparison of displacement for short shells with opening

应力云图结果显示根据传力路径设计的模型使得集中力加载处的应力扩散较快，因此该区域应力水平显著降低，结构最大应力值降低57%。

4 结束语

本文对网格加筋结构中的扩散肋的传力特性和机理进行了深入的发掘，扩散肋布局特征是遵循曲面面内主应力方向，扩散肋截面尺寸特征能够有效控制支反力的数值，因此普遍呈现非均匀分布特征。本文基于扩散肋和筋条的传力机理，提出了一种网格加筋结构的快速设计方法，并将该方法成功应用于平板和曲壳结构。通过大量数值算例的对比，验证了本方法设计的传集中力的网格加筋结构能大幅提高结构利用效率，值得注意的是，本文提出的设计方法的优化结果为理论最优，并未考虑制造工艺约束，这个问题将在未来的研究中进一步探讨。