“仅用无刻度直尺作图”课堂实践例展与分析
⦿ 甘肃省庆阳市正宁县第四中学 李志明
无刻度直尺作图是尺规作图中的一种,有些省市的中考命题者对此十分青睐.然而,这一内容恰巧是学生的薄弱项,表现出了诸多不足,导致利用无刻度直尺作图题的得分率整体偏低.为此,本文中首先呈现例题及其错误画法,并在分析之后简要说明无刻度直尺的工具属性,最后通过呈现课堂教学片段的方式,和学生探究无刻度直尺作图的方法.
1 例题及其错误画法呈现
例题呈现如下:
如图1所示,四边形AOCB是⊙O内一菱形,且A,B,C都在圆上,请仅用无刻度直尺作出线段OA的中点.
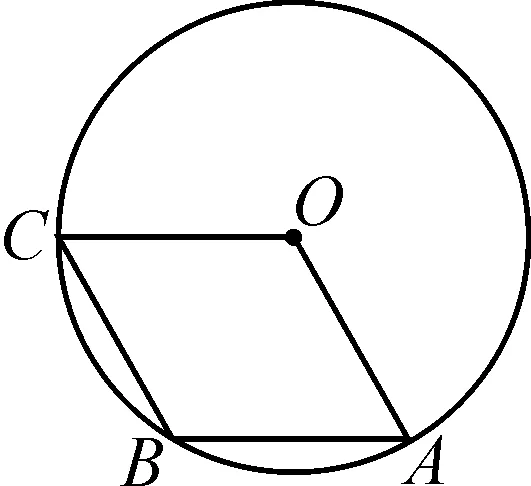
图1
本题图形简单,条件不多,要求也比较明确,难度较小,笔者预估学生完成的质量较高.但从学生的作图来看,存在很多错误之处,下面展示几种错误画法(如图2):

图2
2 错解分析
图2中的四种错解具有代表性.下面对这四种错解进行分析.
图2(1)虽关注到了可用无刻度直尺连接菱形AOCB的对角线构造出点D,但之后直接取OA的中点并连接DE,这正是错误之处.因为仅用无刻度直尺作图时,无法直接且准确地取一条线段的中点,所以违背了无刻度直尺的工具属性.
图2(2)的画法虽然简单,但同样违背了无刻度直尺的工具属性.体现在两个方面:首先,直接取BC的中点;其次,直接取OA的中点.
图2(3)连接BO并延长与⊙O相交于点D,连接DA,作∠BDA的角平分线DE,与OA交于点F,与⊙O相交于点E.这种作法虽部分尊重了无刻度直尺的工具属性,如“连接OB并延长与⊙O相交于点D”“连接DA”,但仅用无刻度直尺难以直接、准确地画出一个角的角平分线.
图2(4)延长CO与⊙O相交于点D,连接DA,连接BD,与OA相交于点E.这种作法虽然准确找到了OA的中点E,每一步操作也符合无刻度直尺的工具属性,但存在多余的线段,应将DA删除.
3 仅用无刻度直尺作图的工具属性说明
从上述四种错解分析中可以看出,违反无刻度直尺的工具属性最常见.那么,无刻度直尺的工具属性有哪些呢?
首先,用无刻度直尺可连接点,如图2(1)中连接CA,OB和图2(4)中连接BD的操作步骤都利用了这一点.
其次,用无刻度直尺可将线段延长,如图2(3)中“连接BO并延长与⊙O相交于点D”和图2(4)中“延长CO与⊙O相交于点D”的操作步骤都利用了这一点.
也就是说,在仅用无刻度直尺作图的情况下,只能进行连接点、延长等操作,不能直接利用无刻度直尺取线段中点、作角平分线、作平行线、作垂线等[1].
4 仅用无刻度直尺作图课堂实践
虽然当前的尺规作图题无需写出作图步骤及证明过程,但这类题处处体现着数学学科特有的逻辑思维[2].那么,该如何引导学生去解决这类问题?下面,展示教学片段:
师:请同学们取出一张白纸,将之折叠再折叠使之成为一把“无刻度直尺”.
学生折纸.
设计意图:长期以来,有刻度的直尺作图给学生留下了极其深刻的印象.用白纸折出“无刻度直尺”,帮助学生脱离有刻度直尺的束缚,是正确利用无刻度直尺作图的关键.
师:请问这样的“直尺”有刻度吗?
生:没有.
师:利用它能否画出一条直线或线段呢?请和同桌交流.
学生交流并分享.
生1:可以画出直线,也可以画出线段,还可以画出射线.
师:请用你的“无刻度直尺”给所画线段找出中点,可以吗?
学生寻找并讨论.
教师巡视并收集错解,在白板上展示.
师:请看白板上展示的两种作法,你认为它们正确吗?
学生观察并思考.
生2:我认为图3的作法不正确.因为仅用无刻度直尺“找”不到它的中点.线段是由无数个点组成的,你怎么知道点O正好就是线段AB的中点呢?所以,我认为这种画法不正确.

图3
生3:我觉得图4的作法也有问题.因为用无刻度直尺画中间直线时,如何知道该直线恰好与线段AB互相垂直呢?
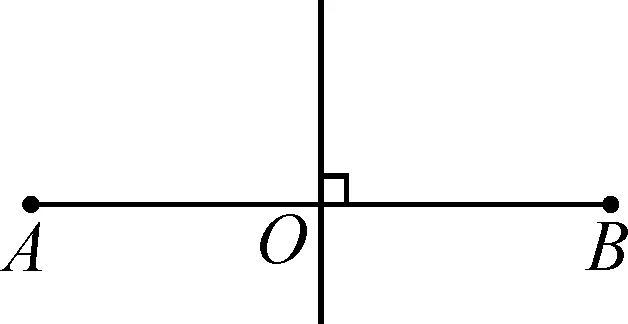
图4
设计意图:收集错解并向学生展示,有利于学生发现问题、分析问题.借助错解让学生反思,更有利于学生形成批判性思维,甚至创造性思维.
师:分析得非常有道理.那么仅用无刻度直尺作图时,到底能做什么呢?
生4:我认为可以连接点.
生5:我认为可以把线段向两端延长.
…………
师:非常好.那么对于图1,应如何利用无刻度直尺作图呢?请思考.
生:(思考)
生6:首先可以把能连接的点用无刻度直尺连接起来,还可以延长线段.如图2(1)中连接OB,CA,如图2(3)中连接OB后延长BO与⊙O交于点D.
生7:线段延长后会产生新的点,这些新的点又可以连接.如图2(4),延长CO,与⊙O交于点D,这个点D就是新产生的点,可以将这个点与其他点连接起来.
生8:我认为还有非常重要的一点,就是把多余的线段去掉,如图2(4)中应该去掉线段AD.
师:大家说得非常好,生8补充得更好.所以,图1中OA的中点可如图5所示作图.
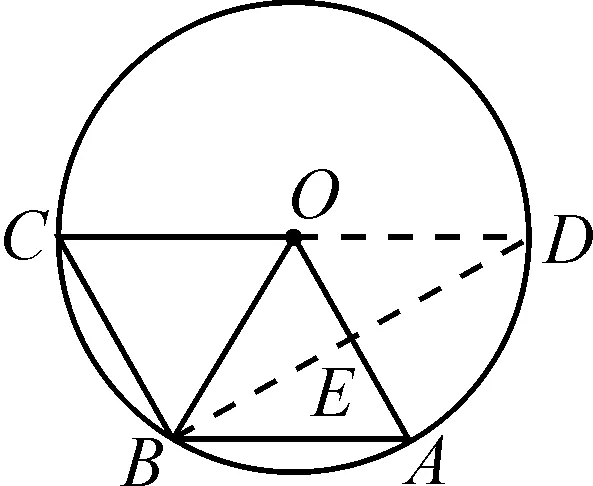
图5
综上所述,在仅用无刻度直尺作图时,一定要摒弃习惯思维对学生的影响,在明确无刻度直尺的工具属性后,才能正确作图.否则,极易出现文中展示的几种错误.

