基于相关性分析小时热负荷影响因素研究

常增军, 薄 盛, 王海超、3, 梅传颂, 李 智, 王海鸿

(1.北京市热力集团有限责任公司,北京100028;2.大连理工大学土木工程学院,辽宁大连116024;3.Aalto大学科学学院,芬兰艾斯堡11100)

1 概述

近年来我国集中供热行业发展迅速,随着人们对室内热舒适性的要求越来越高,按需供热正在成为当前集中供热领域的焦点问题[1-3],模型预测控制将在室温控制中扮演越来越重要的角色[4],准确的小时热负荷预测是模型预测控制不可缺少的一部分,在保障供热效果的同时兼顾节能效果。但小时热负荷的影响因素种类繁多[5-9],若将所有能够收集到的影响因素作为预测模型的输入变量,较多的输入变量不仅会导致计算成本的增加,还会因运算复杂而降低模型精度,因此不能考虑所有影响负荷的因素,需要在预测模型建立前对相关变量进行分析,筛选出影响最大的几个因素作为预测模型的输入变量,以提高模型的实用性和精度。

本研究将大连市某供暖房间作为研究对象,采用DeST能耗模拟软件对供暖房间的热负荷数据进行获取并实验验证,以模拟获取的数据为基础,结合相关分析法对室内设计温度、时间、气象、室内热扰和历史负荷共5类因素与小时热负荷的关联性进行了分析,并对各类因素中影响较大的因素做出了筛选。本文所使用的影响因素分析和筛选方法能够对选择小时热负荷预测模型的输入变量作出指导,对建立高效精准的预测模型具有重要意义。本文中的太阳辐照度未加说明之处指太阳总辐射的太阳辐照度。

2 房间模型建立与验证

2.1 实验房间模型

本文用于热负荷模拟计算的实验房间位于辽宁省大连市,实验房间基本外观见图1,其中实验房间的南北外墙各开设1扇外窗,外门位于北外墙,房间长×宽×高为5 m×4 m×3 m,基本数据见表1,围护结构构造及热工参数见表2。以该房间为研究对象建立物理模型,见图2。实验房间热扰设定见表3。依据表2、3在DeST软件中设定相关参数。

表1 实验房间基本数据

表2 围护结构构造及热工参数

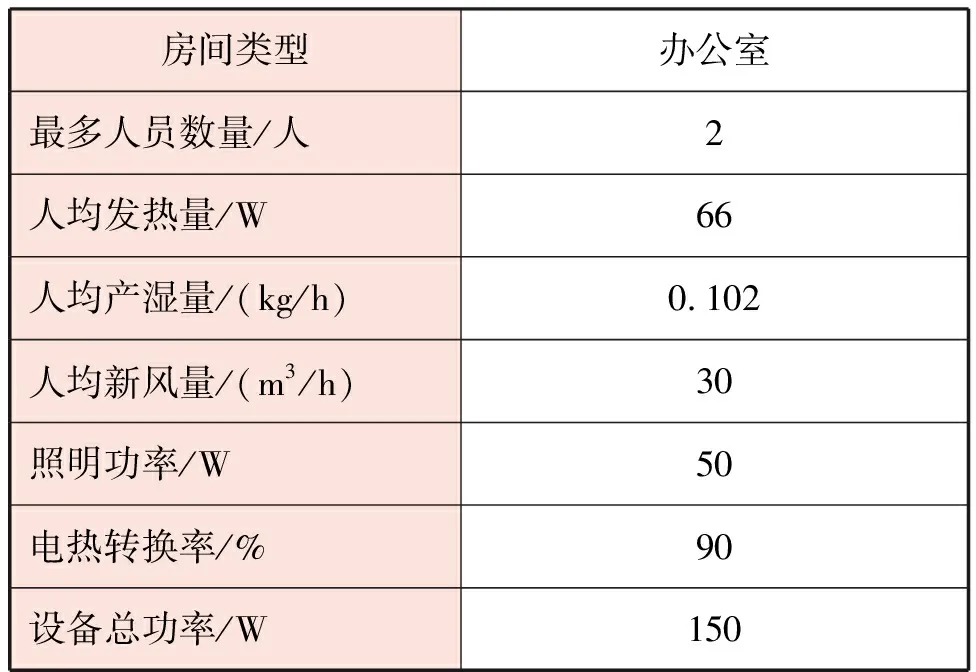
表3 实验房间热扰设定

图1 实验房间基本外观

图2 实验房间物理模型

本文假定实验房间的供热时间为12月1日至次年3月31日,且不单独考虑工作日与节假日,房间每天使用时间为8:00—19:59,共12 h,其中,12:00—13:00为休息时间,室内人员减少,17:00—19:00为晚上工作时间,人员相应减少,19:00—19:59室内人员数为一天内最少,20:00房间停止使用。

结合上述房间使用情况,对实验房间的人员在室率进行设置,因设备使用情况与人员作息相同,所以设备使用率和人员在室率设置相同,人员在室率和设备使用率见图3。实验房间灯光从8:00开始使用,10:00—15:00自然光线充足,仅开启部分灯光即可满足人员工作要求,后续随着室内光线逐渐昏暗,灯光使用率逐渐提高,直至20:00停止使用。实验房间工作日与周末的灯光使用率设置相同,灯光使用率见图4。

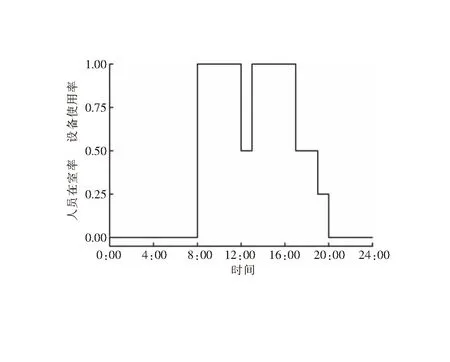
图3 人员在室率和设备使用率

图4 灯光使用率

2.2 模型验证

DeST软件计算以自然室温为基础,选择使用自然室温对模型进行验证,将相同气象条件下自然室温模拟值与实测值进行对比。对2023年2月8日—11日室外干球温度、室外相对湿度、太阳辐照度、室外风速进行实测,实测值分别见图5～8。将实测值输入DeST软件的小时气象数据库文件ClimateData中,得到自然室温模拟值。

图5 室外干球温度实测值

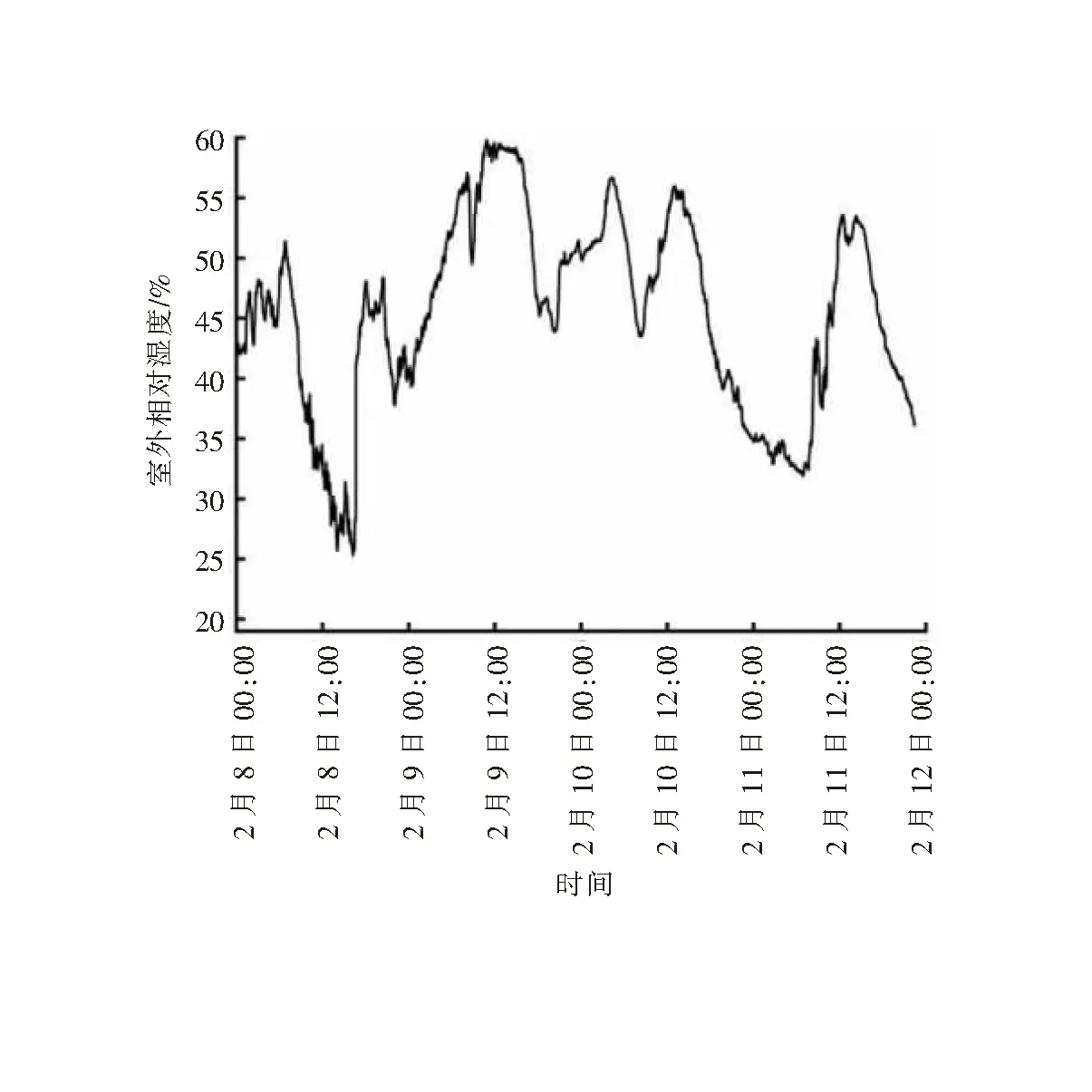
图6 室外相对湿度实测值

图7 太阳辐照度实测值

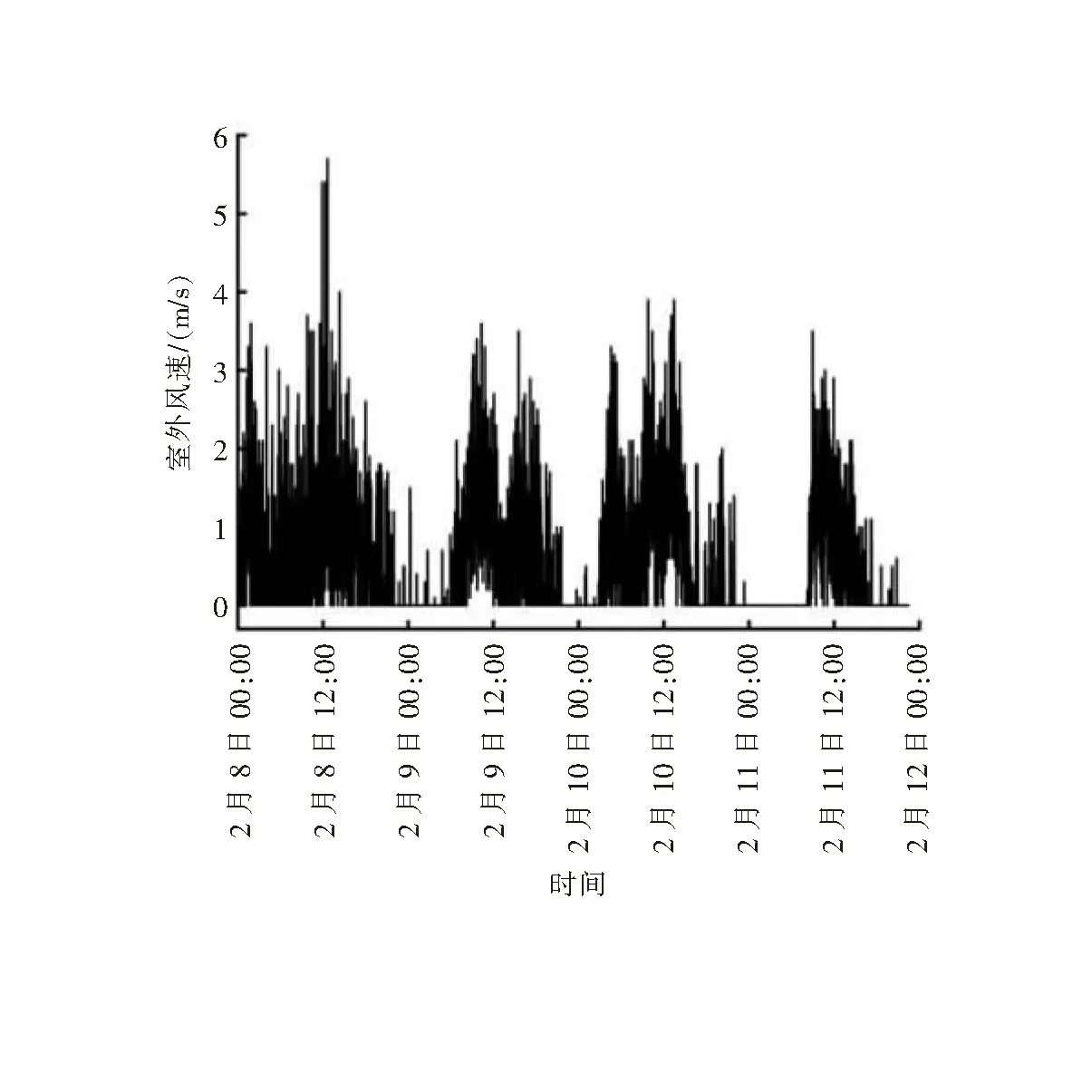
图8 室外风速实测值

根据GB/T 50785—2012《民用建筑室内热湿环境评价标准》,对实验房间测点进行布置,见图9。使用RHLOG智能温度自记仪对2023年2月8日—11日自然室温进行实测,采样时间间隔为1 min,得出所有测点的每小时平均温度作为自然室温实测值,与DeST软件自然室温模拟值对比,见图10。

图9 实验房间测点布置

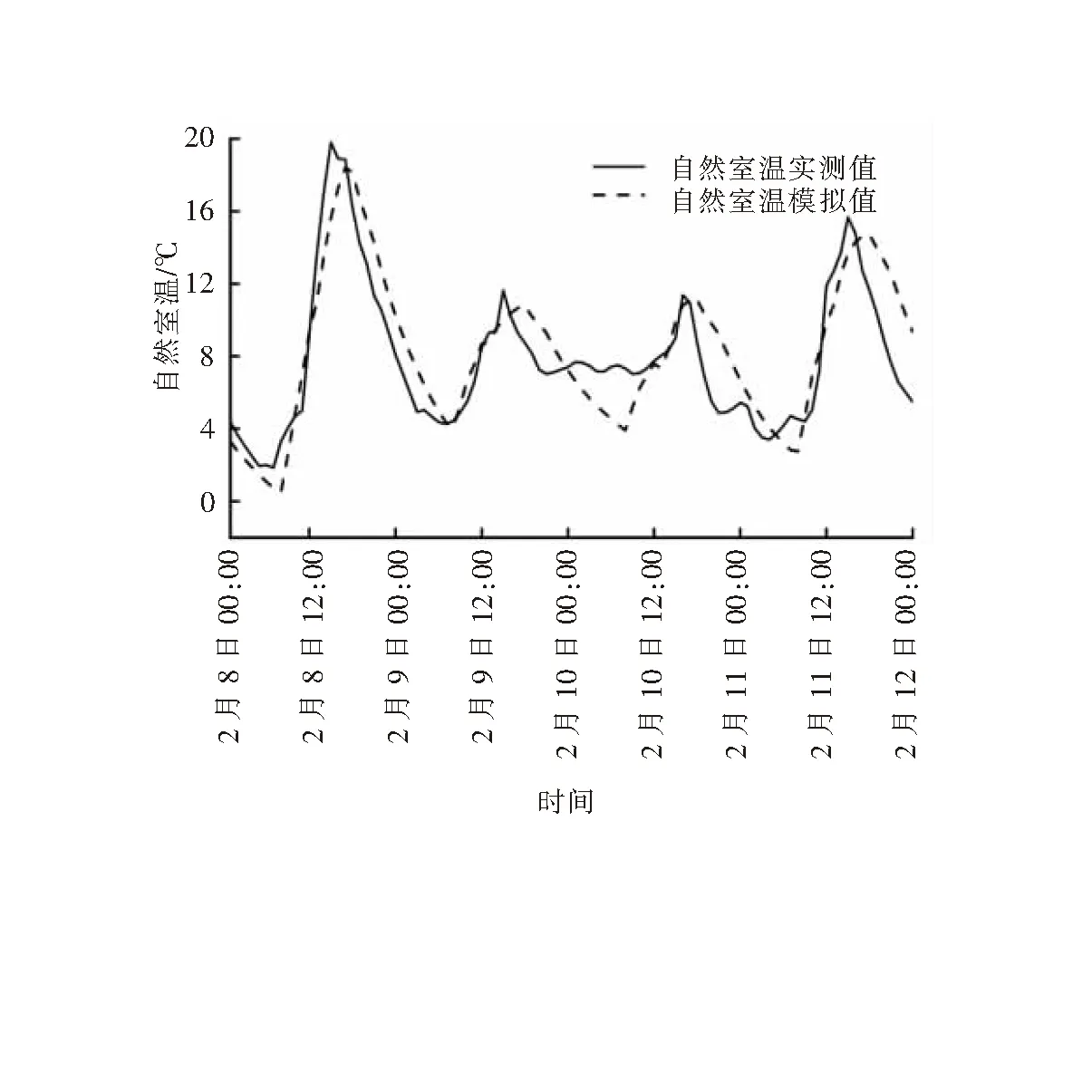
图10 自然室温实测值与模拟值的对比

依据ASHRAE 14—2014《对能源、需求和节水的测量》(Measurement of Energy,Demand,and Water Savings),当归一化平均偏差(NMBE)绝对值小于10%且均方误差变异系数(CVRMSE)小于30%时,模型精度满足要求。归一化平均偏差(NMBE)和均方误差变异系数(CVRMSE)的计算式分别为[10]:

(1)

(2)

式中IN——归一化平均偏差

n——样本数量

Yi,m——时刻i模拟值

Yi,s——时刻i实测值

Yp——实测值的平均值

IC——均方误差变异系数

经计算,本实验房间DeST模型的归一化平均偏差为5.3%,均方误差变异系数为26.4%,模型精度满足要求。证明本研究所建立的DeST模型精确度达到允许范围,使用该模型获得的小时热负荷模拟值能够用来分析热负荷影响因素。

3 小时热负荷影响因素研究方法

3.1 影响因素特征的确定与描述

供暖系统的设计热负荷是指在某一室外温度下,为了达到要求的室内温度,供暖系统在单位时间内向建筑物供给的热量,任何能够改变室外温度或者室内温度的因素都会对热负荷产生影响。本文将室内设计温度纳入影响因素的研究范围,并将小时热负荷的其余影响因素分为时间因素、气象因素、室内热扰因素、历史负荷因素4类。

a.时间因素:选择月、日、是否工作时间,共3项。

b.气象因素:选择DeST软件提供的预测时刻室外干球温度、太阳辐照度、室外相对湿度、室外风速、室外风向,共5项。风向的量化方法见图11,例如,当风向为北偏东25°时,用2表示。

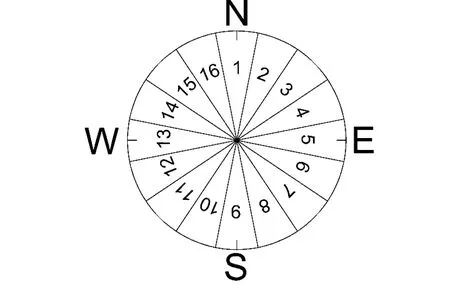
图11 风向的量化方法

c.室内热扰因素:选择人员在室率(设备使用率)和灯光使用率,共2项。

d.历史负荷因素:预测时刻前第1、2、3、6、12、24 h的小时热负荷,共6项。

影响因素描述见表4。接下来将在这18个影响因素中进行筛选,并最终确定小时热负荷预测模型的输入变量。

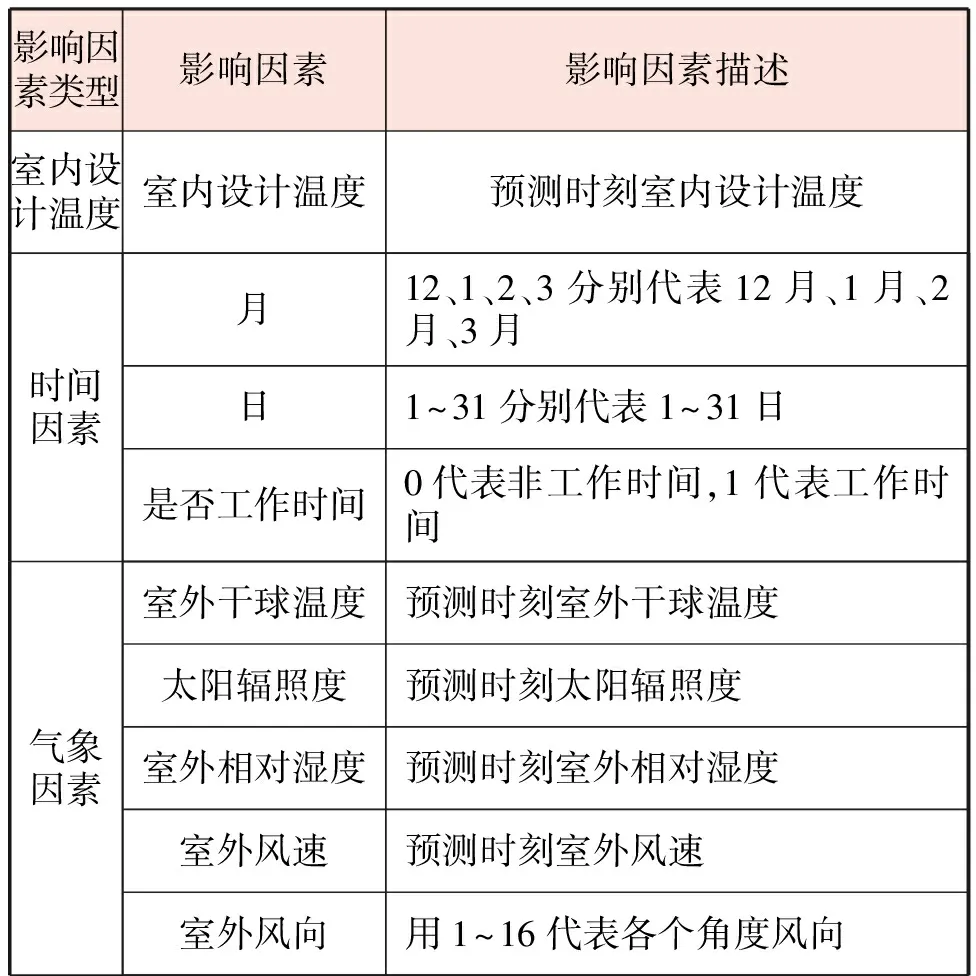
表4 影响因素描述

3.2 室内设计温度分析方法

在DeST软件中设计不同工况,丰富分析用数据,并控制室内设计温度之外的参数不变,量化计算室内设计温度对小时热负荷整体和局部变化的影响程度。我国寒冷地区居民冬季大多在室内活动,室内供暖设施齐全,室内设计温度一般为18～24 ℃。本研究保持实验房间非工作时间的室内设计温度18 ℃不变,对工作时段设置不同的室内设计温度,共计7种工况,见图12。

3.3 基于相关系数法的影响因素分析方法[11-14]

相关系数法属于相关性分析方法中的一种,主要用于对两个或两个以上变量之间的相关程度进行定量分析。相关系数是反映变量间关联程度的量,通过对两个变量的统计分析,得出两个变量的线性关系强度,较为常用的两个相关系数分别是Pearson相关系数和Spearman相关系数,前者要求变量服从正态分布,后者常用于非正态分布变量的相关性研究。

当变量服从正态分布时,通过计算Pearson相关系数[11]进行相关性分析。相关系数计算完成后,需要进行显著性判断,计算显著性水平P[12],并根据P进行显著性判断,其目的是证明数据偶然性不会对相关性判断造成影响。普遍来说,当P小于0.05时,计算结果显著,具有统计学意义,认为计算得到的相关性不是由于随机采样造成的。

当变量不服从正态分布时,使用Spearman相关系数[13]进行相关性分析,Spearman相关系数可以看作是Pearson相关系数的非参数检验形式。Spearman相关系数计算完成后,同样需要进行显著性判断。

本研究使用SPSS软件计算Pearson相关系数和Spearman相关系数,并对其进行显著性判断。

统计学对相关系数r的范围和与之对应的相关程度进行了规定[14],x表示各影响因素,y表示小时热负荷。具体如下。

a.当|r|=1时,x和y完全线性相关。

b.当0.8≤|r|<1时,x和y高度相关。

c.当0.5≤|r|<0.8时,x和y中度相关。

d.当0.3≤|r|<0.5时,x和y低度相关。

e.当|r|<0.3时,x和y弱相关。

f.当r>0时,x和y正相关。

g.当r=0时,x和y不相关。

h.当r<0时,x和y负相关。

当影响因素与小时热负荷的相关系数绝对值大于等于0.3,且显著性水平P小于0.05时,认为二者具有相关性。但由于历史负荷因素内部已经具有了极强的关联性,因此本文认为相关系数绝对值大于0.8,且显著性水平P小于0.05的历史负荷因素与小时热负荷具有相关性。

为了排除室内设计温度变化带来的影响,选择工况1(室内设计温度保持18 ℃)进行相关性分析。经过正态分布检验后,确定时间因素、气象因素、室内热扰因素使用Spearman相关系数进行分析,历史负荷因素使用Pearson相关系数进行分析。

4 小时热负荷影响因素分析结果

4.1 室内设计温度分析结果

在大连市典型年气象参数下,通过DeST获得在整个模拟供暖时段各工况小时热负荷平均值,见表5。小时热负荷平均值随工作时间内室内设计温度上升而上升,室内设计温度每上升1 ℃,小时热负荷平均值平均增加3.5%。

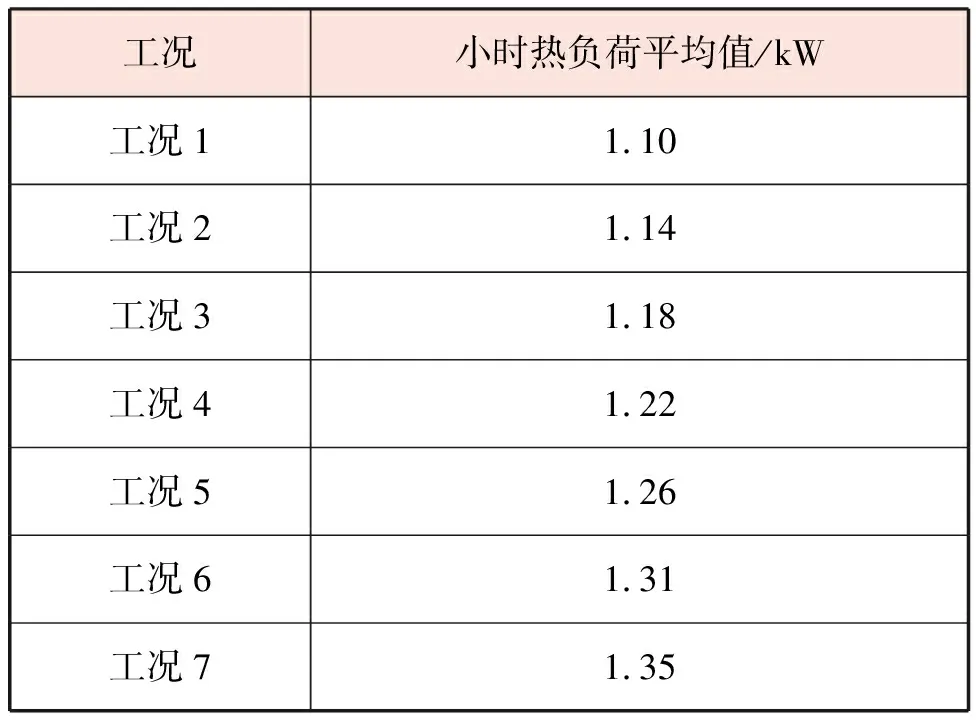
表5 各工况小时热负荷平均值

不同工况下小时热负荷变化情况见图13。8:00房间开始投入使用时,工况1保持室内设计温度不变,房间小时热负荷会因其他影响因素的综合作用而降低。工况2～7将室内设计温度进行不同程度的上调,均造成小时热负荷上升。20:00房间结束使用,工况1保持室内设计温度不变,小时热负荷随着其他影响因素的综合作用而上升;工况2～7将室内设计温度从不同值降低至18 ℃,均造成小时热负荷下降,下调前室内设计温度越高,调整后的小时热负荷越低,这是由于房间的保温作用,下调前的室温越高,同等时间后,室内剩余热量越多,故而热负荷越低。

通过分析和计算得出,室内设计温度对小时热负荷的影响明显,室内设计温度应作为小时热负荷预测模型的输入变量。

4.2 基于相关系数法的影响因素分析结果

① 时间因素

时间因素类影响因素与小时热负荷的Spearman相关系数见表6。

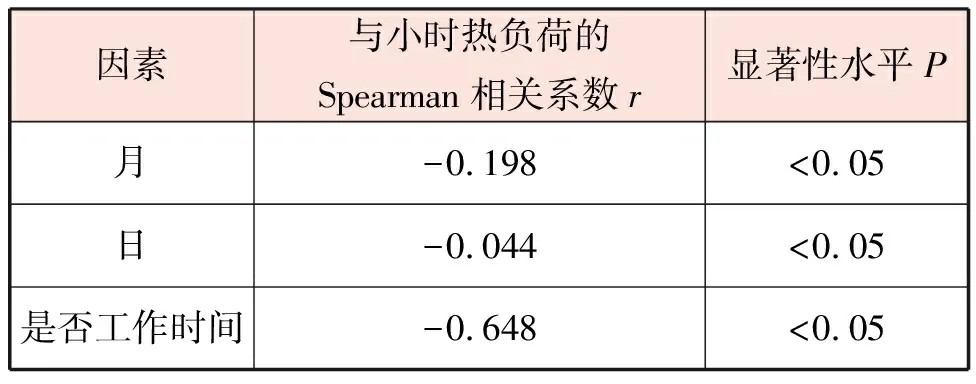
表6 时间因素类影响因素与小时热负荷的Spearman相关系数

是否工作时间与小时热负荷中度负相关,月、日与小时热负荷相关系数的绝对值低于0.3,弱相关。时间因素中,是否工作时间与小时热负荷的相关性最大,在房间投入使用时,人员、设备、灯会产生热量,这部分热量会降低房间的热需求;若房间停止使用,人员、设备、灯停止产热,热负荷随之上升。

由于小时热负荷的时间步长为小时级别,月、日的时间步长过大,对小时热负荷产生的影响很小。因此,只将时间因素中是否工作时间作为预测模型的输入变量,0代表非工作时间,1代表工作时间。

时间因素类影响因素筛选过程中,应首先考虑影响因素与预测热负荷的时间尺度是否在相近的级别,时间尺度相差越大,相关性越小。

② 气象因素

气象因素类影响因素与小时热负荷的Spearman相关系数见表7。

室外干球温度与小时热负荷为中度负相关,室外干球温度越低,小时热负荷越高,与其他气象因素相比,室外干球温度与小时热负荷的相关程度最高,由此推断室外干球温度是对小时热负荷影响最大的气象因素。太阳辐照度与小时热负荷也呈中度负相关,而且与室外干球温度相比其影响尽管稍微小一点,但不能忽视,因此传统地将太阳辐射热作为自由热而不计入负荷影响因素或简单考虑负荷修正系数的方法是不合理的。其他气象因素类影响因素与小时热负荷为弱相关,认为不对小时热负荷产生影响。

因此,本研究将气象因素中的室外干球温度和太阳辐照度作为预测模型的输入变量。

③ 室内热扰因素

室内热扰因素类影响因素与小时热负荷的Spearman相关系数见表8。

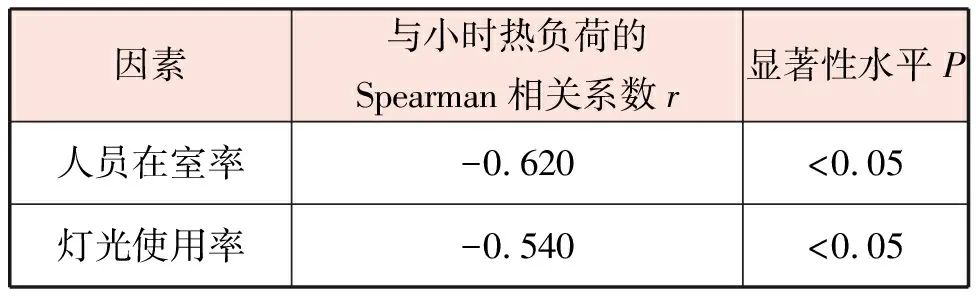
表8 室内热扰因素类影响因素与小时热负荷的Spearman相关系数

人员在室率和灯光使用率与小时热负荷呈中度负相关,证明室内热扰因素能对小时热负荷产生较大影响。

在负荷预测的过程中,需要将室内热扰因素考虑在内,将人员在室率和灯光使用率作为预测模型的输入变量。

④ 历史负荷因素

历史负荷因素类影响因素与小时热负荷的Pearson相关系数见表9。

表9 历史负荷因素类影响因素与小时热负荷的Pearson相关系数

预测时刻前第1 h的小时热负荷与小时热负荷相关性最强,预测时刻前第2 h的小时热负荷的相关性次之。

本研究以Pearson相关系数绝对值0.8为界,确定预测时刻前第1、2、24 h的热负荷作为预测模型的输入变量。

4.3 影响因素筛选结果汇总

通过以上分析,最终确定9个影响因素作为预测模型输入变量,见表10。

5 结论

① 室内设计温度对小时热负荷的影响明显。

② 时间因素类影响因素筛选过程中,应首先考虑影响因素与预测热负荷的时间尺度是否在相近的级别,时间尺度相差越大,相关性越小。

③ 传统的将太阳辐射热作为自由热而不计入负荷影响因素或简单考虑负荷修正系数的方法是不合理的。

④ 室内热扰因素能对小时热负荷产生较大影响,在负荷预测的过程中,需要将室内热扰因素考虑在内。

⑤ 预测时刻前第1 h的小时热负荷与小时热负荷相关性最强,预测时刻前第2 h的小时热负荷的相关性次之。

⑥ 对大连实验房间小时热负荷影响程度较大的影响因素包括室内设计温度、是否工作时间、室外干球温度、太阳辐照度、人员在室率、灯光使用率以及预测时刻前第1、2、24 h的小时热负荷。