ARJ 21飞机起飞速度全局优化方法及效果

王可, 郝欣洁, 孙宏

(中国民用航空飞行学院飞行技术学院, 广汉 618307)

最大起飞重量是制约民用运输机商载能力的主要因素。最大起飞重量的确定不仅要结合飞机自身气动、动力特性和实际运行环境,还须综合考虑多个限制条件的叠加影响。目前,国产民机ARJ 21飞机的制造商提供的飞机飞行手册以及配套性能分析工具仅支持选用平衡起飞决断速度V1起飞[1]的放行方法,同时也将安全起飞速度与参考失速速度的比值V2/VS限定为固定值1.178,由此得到的最大起飞重量相对保守,无法充分发挥机型性能潜力,影响飞机经济性。为改善上述情况,有必要就在可选范围内查找起飞决断速度V1和安全起飞速度V2的最优解进行研究,探寻ARJ 21飞机全局优化可行性,在保证安全前提下挖掘飞机性能潜力,提升起飞装载能力。

在优化必要性方面,王天波等[2]讨论了调整襟翼偏度和使用改进爬升进行起飞性能优化的益处;Prado等[3]通过研究气候变化对商业航空的影响,进行起飞距离计算的灵敏度分析研究;Melis等[4]分析了商载增加对商用飞机关键性能特征的影响特性;潘军等[5]使用神经网络算法优化了起飞决断速度的计算;魏志强等[6]建立了基于遗传算法的双表速爬升优化模型得到航路飞行中近似最佳爬升策略;Hou等[7]讨论了一个固化的改进爬升V2/VS值无法因地制宜满足跑道需要。在优化可行性方面,Setayandeh等[8]讨论了使用遗传算法对无人机进行设计优化;赵向领等[9]将遗传算法应用于航空器载重平衡的研究;Boutemedje等[10]使用遗传算法与人工神经网络来确定最佳无人机的机翼平面参数;Vilela等[11]使用遗传算法进行飞机机翼的设计优化;Jiang等[12]基于多岛遗传算法对喷气翼型气动外形进行优化;Kor等[13]利用遗传算法获得空气动力学最佳几何形状。以上研究未讨论遗传算法与起飞速度优化的相关问题。

综上,现以ARJ 21飞机为研究对象,通过仿真计算,分析在合理范围内同时调整起飞速度V1和V2对起飞限重的影响规律,讨论对V1/VR和V2/VS实施全局优化来进一步提升放行许可最大重量的可行性,并基于遗传算法构建一种全局优化计算方法,旨在为国产支线及干线民机提升适应性和竞争力提供参考。

1 起飞速度全局优化原理

1.1 最大起飞重量的影响因素

放行许可最大起飞重量是结构、场长、刹车能量、轮胎速度、爬升梯度和障碍物等一系列限制结果的最小者。除了结构限制是由适航审定获得并固化在飞机飞行手册中外,其余限制可统称为性能限制,皆与航班实际运行条件密切相关。

影响飞机性能的运行条件较多,若细分,按大气环境可分为气压、温度、风向、风速等;按跑道环境可分为跑道长度、跑道坡度、跑道宽度、道面状态以及障碍物距离、障碍物高度等;按飞机自身状况可分为襟翼形态、重心、空调引气、防冰引气、推力等级等;按操纵条件还可分为V1、V2。

结合性能限制和运行条件,评定最不利结果即最大起飞重量的过程被业界称为起飞性能分析。在此基础上,调整部分可控因素改善最不利结果的过程被业界称为起飞性能优化。对可控因素准确分析有助于在满足适航要求的基础上探究释放飞机潜力的可行性。实际航班放行时,可斟酌的可控因素主要为襟翼形态、引气(空调或防冰)、V1和V2。

由于ARJ 21飞机仅允许“CONF 2”一种襟翼形态起飞,故该参数不具备优化可能;起飞时是否关闭引气取决于天气条件和安全风险,高温环境必须开空调,积冰环境必须开防冰,故该参数也不具备优化可能;所以性能优化重点须着眼于V1和V2。

CCAR 25.107和CCAR 25.103对V1、V2以及相关的VR、VS进行了定义和陈述[14-15]。VS特指FAR 25第108号修正案和CCAR 25第四次修订引入的基准速度VSR。此外,出于行业考虑,速度单位使用节(kt),1 kt=1.852 km/h;高度单位使用英尺(ft),1 ft=0.304 8 m。

起飞决断速度V1是飞行员可以安全实施中断起飞的最晚时机,需满足:

VMCG+ΔV≤V1≤min{VR,VMBE}

(1)

式(1)中:V1为起飞决断速度,kt;VMCG为地面最小操纵速度,kt;VMBE为最大刹车能量速度,kt;VR为抬前轮速度,是飞行员开始向后拉杆使飞机机头抬起以达成离地腾空条件的速度,kt,VR的选取受V2约束。

飞机在一发失效后,在VR抬轮在VLOF离地并达到高于起飞表面35 ft时的速度。需满足:

V2≥1.13VSR且V2≥1.10VMCA

(2)

式(2)中:V2为安全起飞速度,kt;VSR为CCAR 25第四次修订后引入的参考失速速度,kt,统一记为VS;VMCA为空中最小操纵速度,kt。

1.2 V1和V2对起飞的影响

调整起飞速度会影响飞机起飞性能进而影响起飞航迹,如图1所示。

起飞航迹按规章定义可分为场道阶段和航道阶段,航道阶段也称起飞飞行航迹。飞机在场道阶段主要受场长限制,在航道阶段主要受爬升梯度限制和越障限制。改变V1和V2催生不同的起飞航迹,并致使场长、爬升梯度和障碍物对限重构成的最不利影响也不同。

1.2.1 场道阶段

对于场道阶段,飞机受包括起飞可用距离、起飞滑跑可用距离、中断起飞可用距离在内的跑道可用长度制约。中断起飞或继续起飞由加、减速运动中的一种或两种组合而成。由牛顿第二定理可得到沿跑道方向的动力学方程为

(3)

(4)

式中:FN为发动机推力,N;D为气动阻力、风车阻力和偏航阻力之和,N;L为升力,N;W为飞机重力,N;μ为滚动或制动摩擦因数;Wφ为跑道坡度造成的重力分量,N;a为加速度,m/s2;g为重力加速度,m/s2;CD为阻力系数;CL为升力系数;q为动压,Pa;SW为机翼面积,m2。

对于继续起飞,飞机离地上升至35 ft时既加速又爬升,同时机体绕重心产生俯仰方向转动,可沿速度方向和垂直于速度方向构建简化动力学方程,分别为

(5)

(6)

式中:θ为上升角。

由式(3)～式(6)可知,V1的大小既影响中断距离又影响继续起飞距离,且对二者影响相异;V2的大小既影响继续起飞时的地面段长度又影响离地后的空中段长度,由于适航审定条款要求VR的选取是以在35 ft达成V2为目的,故对距离的影响主要取决于V2。可见,V1和V2同时影响场道阶段的性能特性。

1.2.2 航道阶段

在航道阶段,飞机受到最小爬升梯度、改平高度、障碍物、发动机满负荷工作时间制约。以ARJ 21飞机为例,规章CCAR 25既要求飞机航道二段爬升梯度≥2.4%,又要求至少保持V2从收完起落架爬升至总航迹高度不低于400 ft处才能够改平增速,且增速至航道三段末的时长不超10 min,还要求此过程净航迹高于障碍物顶点至少35 ft。

民用飞机的起飞飞行航迹可通过结合上述约束条件对式(5)和式(6)进行运动仿真计算得到,可知:V2的大小直接影响飞机的剩余推力FN-D,选用不同的V2会导致不同的爬升能力和增速能力;除V2以外,V1也会影响起飞飞行航迹,如航道三段加速时长和航道二、三段空间结束位置,进而影响飞机与障碍物的空间几何关系。可见V1和V2也同时影响航道阶段的性能特性。

1.3 仿真算法

结合运行条件和性能限制开展性能分析和性能优化的过程,可通过人工查阅机型手册图表和仿真计算两种途径实现。前者仅能够呈现飞行包线范围内数量有限的状态条件且效率低下,一旦需要插值,还会存在较大误差。随着智慧民航发展和国产民机推广需要,无论是设计端还是使用端,利用后者开展飞机性能分析和优化工作日益普遍。

仿真计算实质是依据算法模型和算法流程不断逼近约束边界的过程。仿真算法既影响结果精度也影响计算效率。一个能够兼顾精度和效率的算法是飞机制造商和飞机用户的迫切需要。遗传算法使用选择、交叉和变异算子来模拟生物种群的整个进化过程。其常规算法流程如图2所示,其中虚框内容是对“需求最优值”步骤的进一步说明。

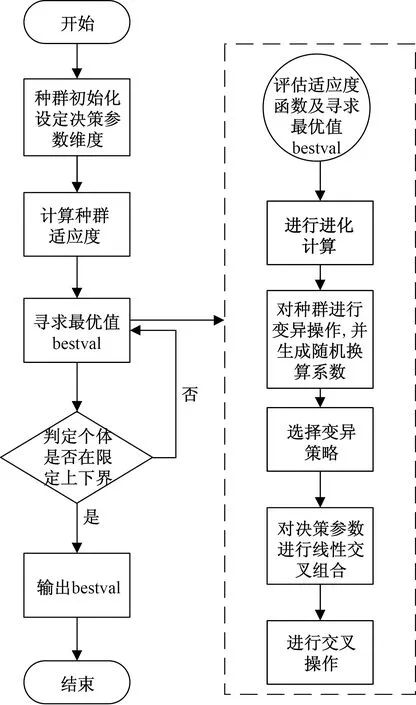
图2 遗传算法程序设计Fig.2 Genetic algorithm programming

遗传算法作为智能优化算法的代表,主要模拟生物进化机制,它的特点是对参数进行编码运算,不需要有关体系的精确方程,沿多种路线进行平行搜索,不会落入局部较优的陷阱,能在许多局部较优中找到全局最优的一种全局最优化方法,相对于传统优化算法,在求解多峰函数极值方面具有一定优势。

将起飞限重视为起飞速度的非显式函数MTOW=f(V1,V2),使用遗传算法在可选V1和V2范围内试探最大起飞重量全局最优解,并评估其计算效率。首先,明确求解问题的编码和解码方式,进行种群初始化pop_XC,设定实际决策参数维度Dim_XC=2,评估适应度函数及寻求最优值bestval;其次,进行进化计算,对种群进行变异操作,生成一个随机的换算系数,选择一种变异策略,进行决策参数的线性交叉组合,进行交叉操作;并将每个个体限制在所给出的上下界限内。

2 起飞速度全局优化分析

2.1 全局优化可选范围

依循业内习惯,在计算最大起飞重量过程中,采用V1/VR和V2/VS两个速度比值作为全局搜索自变量,查找可选范围内能够获得最优解的V1/VR、V2/VS的最佳组合,其目的是分析V1/VR和V2/VS的优选可行性及效果。

因为VR通过试飞确定且与飞机重量有关,V1/VR对起飞性能的影响与V1相仿,故选用V1/VR对V1无量纲化。由于V1不得超过VR,所以最大V1/VR值为1.0;V1可以小于VR,当V1/VR减小时,继续起飞距离增长,中断起飞距离缩短,国外制造商认为当V1/VR小于0.84后,继续起飞距离过长不利于实施,均不建议取最小V1/VR低于0.84。结合ARJ 21飞机特点,在研究中选取的V1/VR优化范围为0.85≤V1/VR≤1。

同样,VS由适航审定方法和飞机重量共同确定,故选用V2/VS对V2无量纲化。考虑到VMCA主要在小重量条件下构成制约,故大重量条件下需着重关注VS,则最小V2/VS为1.13。对于V2/VS的最大值并无明确规定,依机型而异,空客机型最大V2/VS随机型不同为1.4或1.5。ARJ 21飞机性能软件飞行手册模块中限定了最大V2/VS为1.25,故选取V2/VS的优化范围为1.13≤V2/VS≤1.25[16]。

在V1/VR为0.85～1.00、V2/VS为1.13～1.25范围内仿真获得限重结果如图3所示,可见ARJ 21飞机手册中推荐的平衡V1和固定V2/VS=1.178并非最优解。

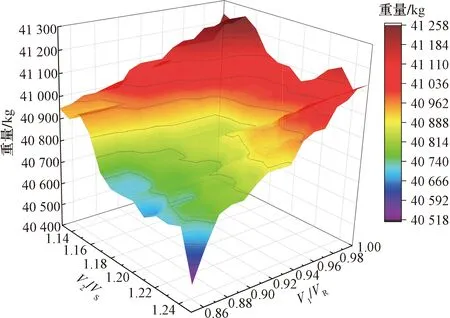
图3 V1/VR、V2/VS全局范围内的最大重量分布案例Fig.3 V1/VR, V2/VS maximum weight distribution cases in full range

2.2 全局优化参数敏感性

通过两个仿真计算实例着重分析了V1/VR、V2/VS对ARJ 21飞机的场长限重、爬升梯度限重、障碍物限重等的参数敏感性。实例1的仿真计算结果如图4和图5所示。

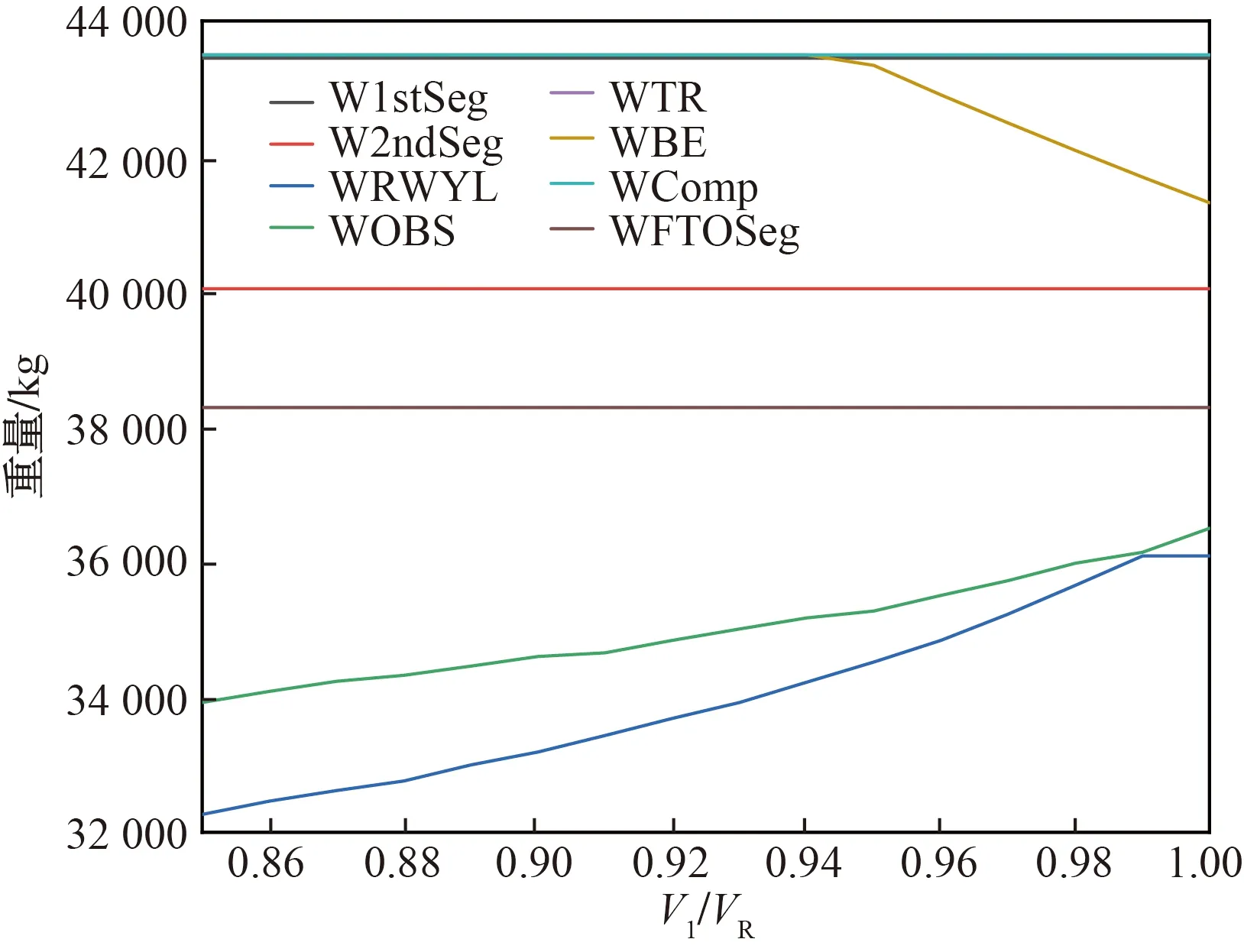
W1stSeg、W2ndSeg、WFTOSeg为航道一、二、四段梯度限重;WRWYL为场长限重;WOBS为障碍物限重;WTR为轮速限重;WBE为刹车能量限重;WComp为结构限重图4 V1/VR对各限制重量的影响Fig.4 Effects of V1/VR on various restricted weights

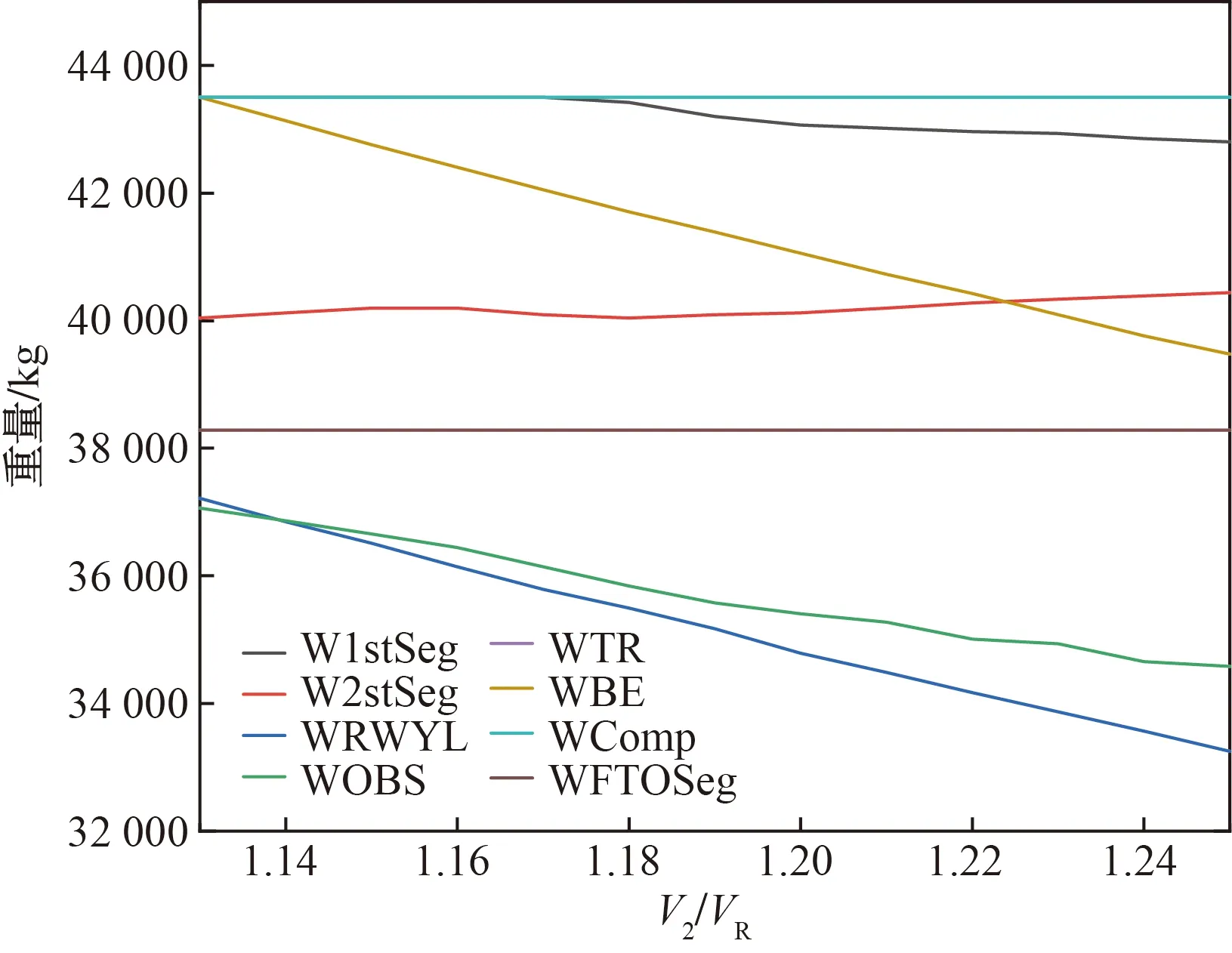
图5 V2/VS对各限制重量的影响Fig.5 Effects of V2/VS on various restricted weights

实例1计算条件:跑道长度LRWY为2 600 m,气压高度PA为2 500 m,温度偏差DISA为30 ℃,停止道长度LStopway为200 m,障碍物OBS距跑道离地端距离和高分别为1 000 m和15 m,静风。分别固定V2/VS、设V1/VR为自变量,固定V1/VR、设V2/VS为自变量。

实例2计算条件:跑道长度LRWY为5 000 m,气压高度PA为2 600 m,温度偏差DISA为22 ℃,障碍物OBS距跑道离地端距离和高分别为1 000 m和15 m,静风。设V1/VR为自变量,分别指定V2/VS为1.178和1.25,仿真计算结果如图6和图7所示。

图6 V1/VR(小V2/VS)对各限制重量影响规律Fig.6 Influence regularity of V1/VR (a smaller V2/VS) on various restricted weights

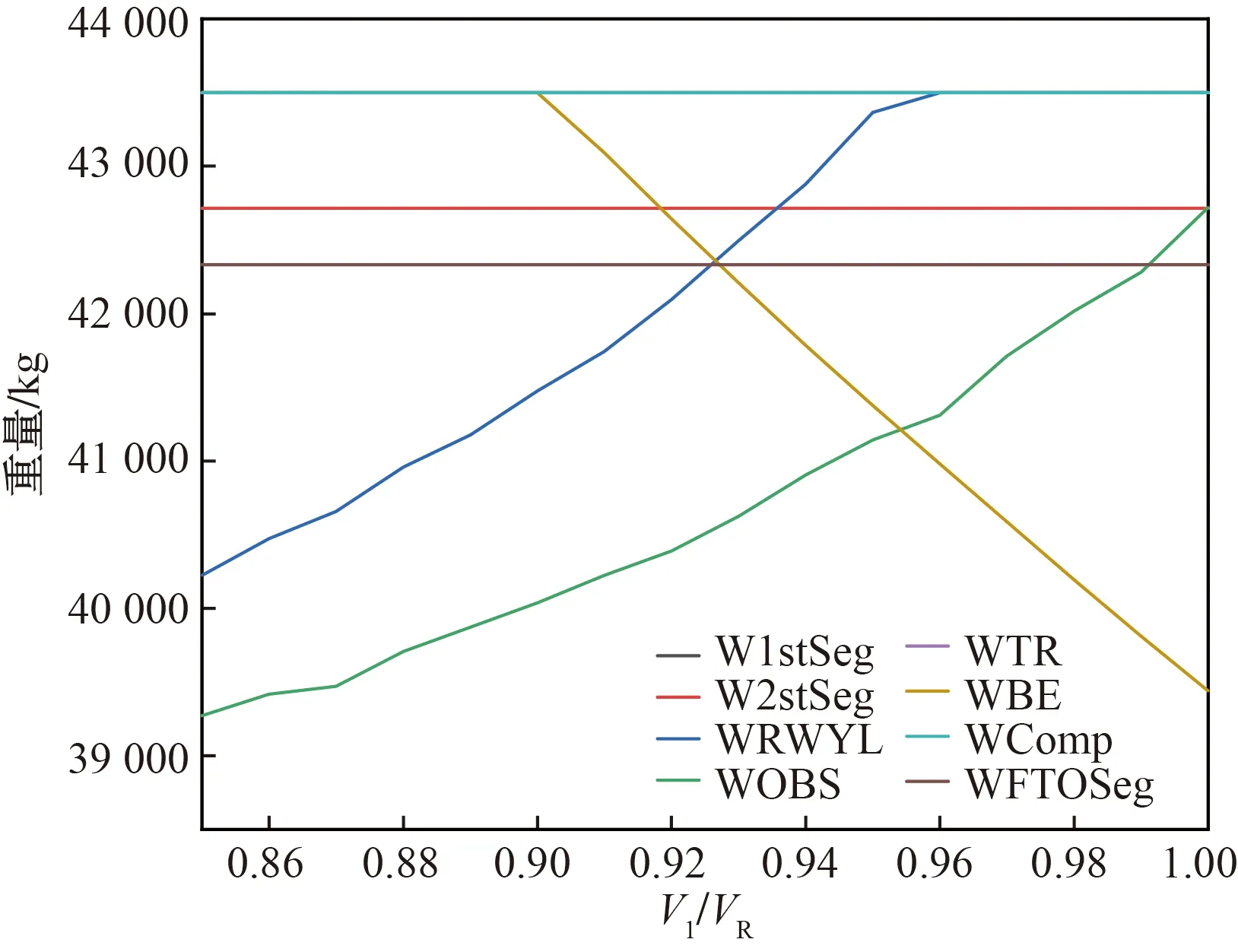
图7 V1/VR(大V2/VS)对各限制重量影响规律Fig.7 Influence regularity of V1/VR (a larger V2/VS) on various restricted weights

图6、图7中,最苛刻曲线下辖区域的最高点即为该条件下最优的最大起飞重量。可见,总是能够在V1/VR、V2/VS各自可选范围内获得一个重量最优值和一个最佳速度比;起飞机场环境条件的改变,会导致最佳速度比、最优值大小、最优值受限形式发生变化;某些条件如图6所示,最优值对应的最佳速度比不是唯一解。

将ARJ 21飞机的各限制重量随V1/VR、V2/VS增加的变化规律简化如表1所示。该规律特性与同类研究结果吻合[17]。

表1 V1/VR、V2/VS对各限制重量的影响规律Table 1 Influence regularity of V1/VR and V2/VS on various restricted weights

2.3 全局优化效果

在上述实例基础上,依据ARJ 21飞机国内实际在运行机场跑道情况,使用飞机手册放行方式和全局优化放行方式进行对比,共计算了4组算例,获得了V1/VR、V2/VS3种不同优化组合下的仿真结果。最后将数值仿真计算结果按跑道平衡与否进行归类,比较了实施平衡起飞方式和全局优化起飞方式对最大起飞重量的影响,如表2、表3所示。

表2 场长限重限制算例仿真结果Table 2 Simulation results of Field lengthlimit takeoff weight limitation calculation example

算例选取结合了目前ARJ 21飞机实际在飞机场和跑道并从NAIP中获得跑道、净空道、停止道的平均长度,同时以高原和高高原的划分作为选定压力高度的依据。算例1、算例2设计了场长限制,起飞滑跑可用距离为2 600 m,无风,标准ISA温度,气压高度分别为1 524 m和2 438 m;算例3、算例4设计了航道二段爬升梯度限制,起飞滑跑可用距离分别为2 800 m和3 100 m,风向风速分别为30 kt和35 kt,ISA偏差分别为-25 ℃和-10 ℃,气压高度分别为1 524 m和2 438 m。

以上算例的停止道长度均为60 m,净空道长度均为200 m,皆为ARJ 21所飞机场统计平均结果向下取整所得。如表2所示,当最大起飞重量受到场长限制时,在平衡跑道以及增加停止道或者净空道的条件下,气压高度PA=1 524 m时,优化V1/VR后的起飞限重平均提升0.75%,优化V2/VS后的起飞限重平均提升4.65%,全局优化后的起飞限重比未进行优化的平均提升5.53%;气压高度PA=2 438 m时,优化V1/VR后的起飞限重平均提升0.71%,优化V2/VS后的起飞限重平均提升4.76%,全局优化后的起飞限重比未进行优化的平均增加5.51%。

如表3所示,当最大起飞重量受到爬升梯度限制时,在平衡跑道以及增加停止道或者净空道的条件下,优化V1/VR后的起飞限重无提升,气压高度PA=1 524 m时,优化V2/VS后的起飞限重平均提升0.83%,全局优化后的起飞限重比未进行优化的平均提升0.95%;气压高度PA=2 438 m时,优化V2/VS后的起飞限重平均提升0.92%,全局优化后的起飞限重比未进行优化的平均提升1.03%。可见,当ARJ 21飞机的最大起飞重量受到场长限制或者爬升梯度限制时,对V1/VR、V2/VS实施全局优化,确能有效增加飞机的最大起飞重量。

2.4 全局优化计算模型及效率

通过计算机仿真完成起飞速度全局优化计算既能够缩短航班航前分析时长,也能够获得更为良好的计算精度。鉴于目前常规载客运输飞机的起飞速度均介于100～200 kt,欲使仿真计算起飞速度精度达到0.1 kt,则V1/VR、V2/VS速度比值的量级至少需要精确到小数点后三位。此时若使用遍历方法求解,在全局优化取值范围内V1/VR需计算150个状态点,V2/VS需计算120个状态点(状态点是指1组V1/VR、V2/VS所对应的最大起飞重量)。在V1/VR和V2/VS两个维度同时使用遍历法开展全局优化查找需至少计算18 000个状态点。经在基准频率1.6 GHz和动态加速频率3.4 GHz的常规台式电脑上测试,使用ARJ 21飞机配套性能软件计算1个状态点所需时长为0.3 s。可知使用遍历法进行全局优化计算获得1组解所需总时长约为90 min。值得注意的是,这仅是1组风温组合下的计算时长,而建立一张实际放行中机组必备的起飞分析通常至少需要170组风温组合(按2组道面状态、5组风速、17组温度),时长为15 300 min。显见,使用遍历法进行全局优化分析完全无法满足实际运行需要,建立既满足精度要求又满足效率要求的算法模型十分必要。

先选用黄金分割法进行速度全局优化计算,并将遍历法和黄金分割法仿真计算结果记录如表4所示,计算条件为:起飞襟翼为CONF 2,温度偏差DISA=15 ℃,修正海平面气压QNH=1 013.25 hPa;静风。

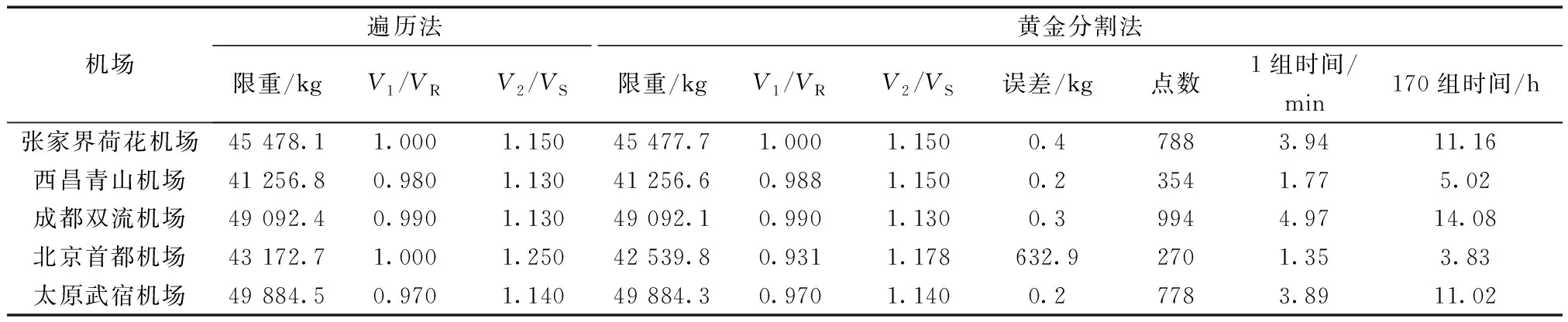
表4 黄金分割法全局优化结果Table 4 Full range optimization results by using golden section method

由表4数据可知,使用黄金分割法进行全局优化计算,绝大部分误差为0.3 kg,但仍有个例误差为632.9 kg情况出现,这是因为二维情况下黄金分割法不一定能够找到全局最优解所致。此时,获得1组解所需平均时间约为3.2 min,计算效率加快了约28倍,即便如此,构建一张起飞分析表按170 组风温组合所需时长为544 min,仍存在优化空间。

有鉴于此,选取遗传算法来进行全局优化模型的构建。使用遗传算法的全局优化计算流程如图8所示。

图8 全局优化流程图Fig.8 Full range optimization flowchart

遗传算法的关键在于符号串表示和遗传操作的设计,建立遗传算法模型步骤如下。

步骤1选择编码策略,采用浮点数编码表示基因,容易理解且不需要解码过程。

步骤2定义合适的适应度函数fitness,保证适应度函数非负。

步骤3确定遗传策略,包括选择群体大小NP,选择、交叉、变异方法,以及确定交叉概率、变异概率等其他参数。

步骤4确定两个变量V1/VR、V2/VS的上下限XCmax(1)(2)、XCmin(1)(2)。

步骤5按照遗传策略,运用选择、交叉和变异算子作用于群体,形成下一代最优值。

步骤6判断所得bestmen-XC最佳真实实际参数,或以完成预定进化代数,若满足则输出最优结果,不满足则返回步骤5,直到得到最终的bestval。

3 起飞速度全局优化算例

使用遗传算法的计算条件:起飞襟翼为CONF 2,温度偏差DISA=15 ℃,QNH=1 013.25 hPa;静风,对5个城市机场用遗传算法进行全局优化计算,分别设定遗传进化代数itermax为5(相应程序计算状态点为120 个)、10(相应程序计算状态点为220 个)、20(相应程序计算状态点为420 个),得到的寻优结果如表5、表6所示。

表5 遗传算法全局优化限重结果Table 5 Full range optimization MTOW result of genetic algorithm

表6 遗传算法全局优化速度结果Table 6 Full range optimizationvelocity result of genetic algorithm

可见,当遗传进化代数itermax=5、10、20时,最大起飞重量出现误差最大值为17.1、0.7、0.4 kg,V1/VR的平均误差为0.004、0.004、0.006,V2/VS的平均误差为0.001、0.000 2、0.002,准确度优于二维黄金分割法。

同样,当遗传进化代数itermax为5、10、20时,一组风温条件下计算的状态点个数分别为120、220、420。仍按一个状态点耗时0.3 s计,获得1组解的时长分别为0.6、1.1、2.1 min,构建一张起飞分析表按170 组风温组合所需时长为102、187、357 min。

综上所述,遗传算法受机场条件影响不显著,结果准确性和计算效率均有进一步提高。

4 结论

以ARJ 21飞机为研究对象,讨论了对V1/VR和V2/VS实施全局优化来进一步提升放行许可最大重量的可行性,并采用3种算法分别搭建全局优化模型进行仿真计算,以遍历法为参照,对比了黄金分割法和遗传算法的计算效率和计算准确性,并使用多个机场实例进行了验算,结论如下。

(1)V1/VR和V2/VS对场长限重、爬升梯度限重均存在综合影响,尽管部分限重类型存在与V1/VR和V2/VS其中之一不相关的情况,但最终仍会使得放行许可最大起飞重量发生改变。

(2)对V2/VS实施优化的效果优于V1/VR,二者同时开展全局优化对放行许可最大起飞重量的提升效果更加显著。

(3)使用速度全局优化构建起飞分析表存在巨大的运算量,且放行条件的动态变化致使无法采用预生成的方式进行简化,必须寻求优化算法提升运算效率。

(4)使用遗传算法能够获得比黄金分割法更好的计算精度和计算效率,且相对于遍历法计算效率提升十分显著,是一种可供制造商选用的全局优化计算方法。

尽管使用了遗传算法针对ARJ 21最大起飞重量进行全局优化计算进行了研究,也获得了在精度和效率方面的良好效果,但与国际主流制造商机型配套性能软件(如空客PEP)相比,构建基于全局优化方法的起飞分析表的效率仍然存在差距,还有进一步提升的空间。此外,仅针对干、湿跑道条件下的起飞实施了全局优化研究,后期可进一步探讨污染跑道条件对全局优化的收益影响。