船-缆-机器人采矿系统中非均匀张力缆振动特征分析

程阳锐, 马佳乐, 王振, 戴瑜

(1.中南大学 机电工程学院, 湖南 长沙 410083; 2.长沙矿冶研究院有限责任公司, 湖南 长沙 410012; 3.深海矿产资源开发利用技术国家重点实验室, 湖南 长沙 410012; 4.大连理工大学 数学科学学院, 辽宁 大连 116024; 5.北京航空航天大学 数学科学学院, 北京 100191)

当前,开发利用海洋矿产资源逐渐成为国际社会海洋竞争的焦点,各国参与深海矿产资源勘探开发进度提速,深海矿产资源开发已进入快速发展阶段[1]。2020年,ABS发布了《海底采矿指南(ABS Guide for Subsea Mining)》[2],2021年比利时GSR公司完成矿区采矿试验及环境影响研究,海洋采矿已经近在咫尺。我国自20世纪80年代以来,逐渐完成深海采矿技术装备从陆地到海洋,从单体到系统联动的跨越,当前正准备开展实际矿区的采矿技术研究。深海多金属结核是当前公认最有可能首先实现商业开采的矿种,研究表明,多金属结核主要含有的锰、镍、铜、钴等金属的总储量高出陆地储量几十倍到几千倍,具有很高的经济价值[3]。多金属结核主要分布在水深2 000～6 000 m的深海底部,将其从数千米深海底开采出来需要依靠独特和高效可靠的开采技术和装备[4-5]。开展采矿的前提是进行详细的多金属结核矿勘探,当前众多勘探装备均是采用脐带缆与水下作业设备进行连接,例如集矿车、水下机器人等。在受到复杂海况、海流等影响,连接线缆出现无规则运动,直接影响海底作业设备的稳定性,导致无法正常作业。所以开展船-缆-机器人的作用机理研究,找出缆索端部运动对非均匀张力缆的振动响应,对海上作业具有重要的指导意义。

目前缆索的动力分析方法主要可分为有限元法、有限差分法和集中质量法等。Ablow等[6]利用有限差分法提出了水下缆索在时间和空间上的离散数值模型并求解;Milinazzo等[7]在Ablow建立的三维模型基础上作出改进,提出了一种模拟拖缆系统三维运动的有效算法;李力波[8]基于上述方法采用三维动力学模型模拟分析了缆索系统的多种运动情况,并对缆的受力分析和运动方程较原有模型有所改进。Gobat等[9]利用有限差分法对水下缆索进行了时间域模拟,并通过α时间积分算法、自适应时间步长和自适应空间网格化分析了电缆的二维静态和动态效应。Eidsvik等[10]利用有限元方法,基于欧拉-伯努利梁方程建立了ROV脐带缆模型,并通过脐带缆和ROV系统的稳态和动态响应的数值算例验证了所提出的模型。刘铭等[11]基于集中质量法,推导了拖曳缆索动力学方程,考虑了缆索的外载荷、拉伸和弯曲刚度,模拟了拖船在各种运动情况下缆索系统的动力响应。Quan等[12]提出了一种具有几何非线性运动的变长度水下缆索有限元模型,考虑了轴向载荷、剪切、弯曲和扭转的影响,并通过实例对所提出的模型及其求解方案进行了验证。Chen等[13]基于Kirchhoff杆理论建立了复杂海况下脐带缆的动力学模型,分析了不同条件下脐带缆的运动和受力特性。郑鹏等[14]基于Ablow提出的缆索偏微分控制方程,采用有限差分法建立了潜水器-缆索-载荷三者间相互耦合的动力学模型,通过数值仿真方法分析了缆索收放过程的动态响应特征。

当前对于非均匀缆索的动力学分析主要采用数值模拟方法,而对非均匀缆索的理论分析较少,通过对非均匀张力缆振动的自然频率分析,对直接影响缆索的共振响应分析,进而对海上作业提出建议。本文针对船-缆-机器人采矿系统的共振等危险工况,研究缆索振动的自然频率及其对应的模态函数。首先基于缆索的非均匀张力特征给出变系数微分方程;然后基于变量分离法,结合边界条件和初始条件求解模型并得到控制方程关于解的Bessel函数表达式;最后分析采矿船和水下机器人运动时改变相应的边界条件,所引起的缆索振动响应特征。

1 数学模型

当缆索受到的外部激励频率和缆索的自然频率接近或相等时,会产生缆索的共振,外部激励主要为海流、波浪等外部时变载荷,在控制方程中主要表现为外力项。缆索的自然频率是缆索的固有性质,它和缆索的长度、张紧程度、边界条件、材料等物理属性相关,和外载荷无关。接下来在不考虑海流作用和海水的附加质量的假设下,对船-缆-机器人系统做如下假设,不带浮力块的均匀缆索处于垂向状态,其内部张力沿垂向可变,建立线性数学模型并分析其自然频率和模态函数及其影响因素。

1.1 控制方程

如图1,考虑缆索上端为采矿船,缆索末端为可移动的水下机器人装备。记机器人在水下的总质量为m1(kg),缆索总长度为L(m),单位长度缆索在海水中的质量为m2(kg)。以x轴方向为缆索垂直向上的方向,u轴方向为静止水面所在的水平方向建立坐标系,用u(x,t)表示缆索上各点在时刻t沿垂直于x方向的位移。缆索的截面直径与缆索的长度相比可以忽略,缆索上各质点间的张力方向与缆索的切线方向一致,忽略弯曲、扭转和剪切力的影响,且缆索处于张紧状态。

图1 船-缆-机器人采矿系统

缆索的张力由上到下由于自重影响逐渐减小,则x点处的张力为:

T(x)=m1g+(x+L)m2g

且T(x)的方向总是沿着缆在x点处的切线方向。如图2所示,在缆上任取一段小微元(x,x+Δx),则在x点处作用于缆段(x,x+Δx)的张力在水平方向上的投影为:

图2 缆索局部受力示意

Tu(x)=[m1g+(x+L)m2g]sinθ(x)

式中θ(x)表示张力T(x)的方向与x轴的夹角。在缆段的另一端x+Δx点处作用于缆段(x,x+Δx)的张力在水平方向上的投影为:

Tu(x+Δx)=[m1g+(x+Δx+L)m2g]sinθ(x+Δx)

式中θ(x+Δx)表示张力T(x+Δx)的方向与x轴的夹角。假定缆索在某一平面内作微小横振动,即当θ足够小时,有:

sinθ≈tanθ=∂u/∂x

沿垂向受力分析可知:

T(x)cosθ=T(x+Δx)cosθ(x+Δx)

当Δx足够小时,可以得到T(x)在微元处相等。基于牛顿第二定律,考虑缆索在横向运动的受力平衡有:

两端同时除以Δx,再令Δx→0取极限得:

于是得到缆索在x∈[-L,0]上的控制方程u(x,t)满足:

(1)

1.2 初边值条件

假设采矿船和水下机器人在海平面内运动,忽略垂向运动,并考虑缆索在给定海流方向下的二维横向振动问题。其三维横向振动问题在线性假设下可分解为2个二维问题并进行叠加。设采矿船的运动位移随时间函数为h(t),水下机器人的运动位移随时间函数为g(t),即缆索在x=0处和x=-L处的边界条件为:

u(0,t)=h(t),u(-L,t)=g(t)

(2)

此外,缆索在初始时刻t=0时的位移和速度给出系统的初值条件,本文为简便,考虑初始状态为静止的情形,即:

u(x,0)=0,ut(x,0)=0

(3)

综合缆索的运动控制方程(1)和边界条件(2),以及初始条件(3)组成的初边值问题:

该系统描述了缆索在可移动边界条件下的运动,可用于分析端部运动对缆索振动特征的影响。

2 解析求解

系统(Ⅰ)为非齐次边界条件的缆索运动控制问题,欲对其解析求解,需首先将非齐次边界条件转化为齐次边界条件,可通过如下变换进行。令:

U(x,t)=h(t)-x(g(t)-h(t))/L

(4)

作v(x,t)=u(x,t)-U(x,t),并记:

F(x,t)=x(g″(t)-h″(t))/L-h″(t)-

H(x)=-h(0)+x(g(0)-h(0))/L

G(x)=-h′(0)+x(g′(0)-h′(0))/L

可得v(x,t)满足下面的非齐次方程、齐次边界条件和非齐次初始条件的系统:

该系统将边界条件的运动转化为初始状态下缆索在外力F(x,t)的作用下的振动特征,同时将运动边界转化为固定边界问题,且系统的初始状态与采矿船和水下机器人的运动初始值有关。

基于叠加原理,将上面的系统 (Ⅱ) 可以通过v(x,t)=v1(x,t)+v2(x,t)分解为下面2个系统(Ⅲ) 和(Ⅳ)的和。

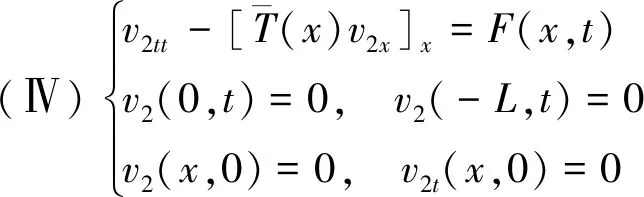
系统(Ⅲ)描述了齐次边界的缆索在不受外力作用下的初边值问题,可通过变量分离法得到非均匀张力缆的自然振动频率和模态函数,对避免共振现象的发生有重要意义;系统(Ⅳ)为齐次边界下静止缆索在外力F(x,t)下的受迫振动问题,该系统和运动的时间变化直接相关。

先求解系统(Ⅲ),利用分离变量法,令:

v1(x,t)=X(x)Z(t)

(5)

将式(5)代入系统(Ⅲ)中方程,得到空间变量满足:

x∈[-L,0]

(6)

及时间变量满足:

Z″(t)+ω2Z(t)=0

(7)

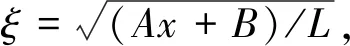
(8)

(9)

可知方程(9)为零阶Bessel方程,通解可以写为:

(10)

(11)

由系统(Ⅲ)中的边界条件:

X(0)=0,X(-L)=0

(12)

将方程的通解式(11)代入式(12)中可得:

(13)

为了使式(13)存在非零解,则需令系数行列式为0,即:

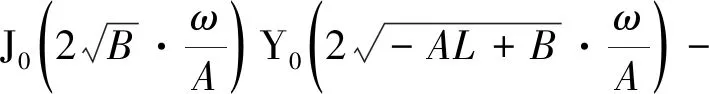
(14)

满足式(14)的ω为模型的特征值,即自然频率,将其从小到大依次排列为ω1<ω2<ω3<…,于是ωk对应的模态函数:

(15)

对vk(x)作归一化处理:

(16)

将特征值ωk代入方程(7)中,可得其通解为:

Zk(t)=Akcos(ωkt)+Bksin(ωkt)

(17)

式中Ak、Bk为任意常数。因此得到:

(18)

又由(Ⅲ)中初始条件,利用Bessel函数正交性可得:

(19)

下面利用齐次化原理[15]求解(Ⅳ),若W(x,t;τ)是方程组:

(20)

(21)

式(21)形式上与(Ⅲ)相同,所以可得:

(22)

由式(21)中的初始条件Wt′|t′=0=F(x,τ)得:

(23)

所以得到(Ⅳ)的解

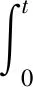
(24)

3 非均匀张力缆的振动分析

假定缆索上端为采矿船,缆索末端为水下机器人,考虑缆索端部船、机器人运动对缆索振动情况造成的影响。下面通过具体的数值算例分析采矿船和机器人运动的幅度及频率对缆索振动的影响。已知水下机器人总质量m1=2 000 kg,缆索总长度L=5 000 m,考虑单位长度缆索在海水中质量为m2=0.972 kg,重力常数取g=9.8 N/kg。

通过求解式(14)可得到该系统的自然频率,对应的式(15)可给出相应的模态函数。具体的前5阶自然频率见表1,前5阶归一化模态函数见图3。

表1 前5阶自然频率

图3 前5阶归一化模态函数

3.1 采矿船运动对缆索振动的影响

首先,考虑采矿船运动幅度和频率对缆索振动幅度的影响。设h(t)=Ausin(ωut),其中Au为采矿船运动的幅度,ωu为采矿船运动的频率;水下机器人静止不动,即g(t)=0,通过改变Au和ωu的值来分析采矿船运动对缆索振幅的影响情况。

由方程(Ⅰ),将h(t)=Ausin(ωut),g(t)=0代入模型的解可得:

(25)

其中:

(26)

(27)

由式(25)～(27)可以得到缆索振幅随Au线性变化。

图4 采矿船运动时前5阶模态函数对应的振动分量随ωu的变化

3.2 水下机器人运动对缆索振动的影响

接下来,考虑水下机器人运动幅度和频率对缆索振动幅度的影响。设g(t)=Adcos(ωdt),其中Ad为水下机器人运动的幅度,ωd为水下机器人运动的频率;缆索上端采矿船静止不动,即h(t)=0,通过改变Ad和ωd的值来分析水下机器人运动对缆索振幅的影响情况。

由方程(Ⅰ),将h(t)=0,g(t)=Adcos(ωdt)代入模型的解可得:

(28)

其中:

(29)

(30)

由式(28)～(30)可得出缆索振幅随着Ad线性变化。

图5 水下机器人运动时前5阶模态函数对应的振动分量随ωd的变化

4 结论

1) 利用分离变量法求解得到非均匀张力缆自然频率和模态函数的解析表达式,进而得出运动控制方程解的Bessel函数精确表达式。

2) 采矿船的运动幅度逐渐增大时,缆索横向最大振幅呈线性增长;运动的频率与各阶自然频率相等时,采矿船和缆索会发生共振现象,缆索的振幅会趋于无穷大,此时应该考虑缆索大变形振动并通过非线性方法进行分析。

3) 水下机器人的运动幅度逐渐增大时,缆索横向最大振幅呈线性增长;运动频率与各阶自然频率相等时,水下机器人和缆索出现共振,缆索的振幅趋于无穷大,此时应考虑缆索大变形振动并通过非线性方法进行分析;水下机器人的运动频率变化时,缆索各阶分量振幅的变化相比采矿船运动频率变化时更平缓。

考虑到海上作业的安全性,在实际应用中首先考虑采矿船在风浪作用下的运动规律,进一步设计缆索从而避免其和采矿船的共振;其次在水下机器人操作过程中通过规划合理的路径和运动方式,避免缆索和机器人产生共振。