海洋柔性管缆整体线型静态快速设计方法

樊耀华, 杨志勋, 王刚, 阎军, 史冬岩, 乐奇, 曹鹏

(1.哈尔滨工程大学 机电工程学院, 黑龙江 哈尔滨 150001; 2.大连交通大学 土木工程学院, 辽宁 大连 116028; 3.大连理工大学 工程力学系, 辽宁 大连 116023)

海洋柔性管缆[1](脐带缆、柔性立管、风电动态海缆等)是海洋浮式生产系统的重要组成设施,由于自身具有良好的弯曲性能,能顺应比较大的浮体漂移,广泛应用于海洋油气开发。在服役时通常受到管缆、内部流体的重力,附属构件(浮筒或浮拱)的浮力以及波浪、流、浮体运动等环境荷载,为了保证柔性管缆在各种荷载的作用下能够正常工作,需要将其设计成一定的几何形态,称之为整体线型设计[2]。目前,柔性管缆整体线型设计采用“静态设计,动态分析”的方法。实际工程中,柔性管缆整体线型初步设计可基于静态分析结果并结合动力放大系数加以进行,从而提高整体线型设计效率[3]。由此可见,柔性管缆整体线型静态设计作为线型设计分析的基础,对快速精确完成整体线型设计具有研究价值。

关于柔性管缆整体线型设计,国内外学者开展了许多研究。Chandwani等[4]总结了柔性管缆常选用的线型,分别为自由悬链线型(free hanging catenary)、缓波型(lazy wave)、陡波型(steep wave)、缓S型(lazy S)和陡S型(steep S),为之后的线型设计提供了方向;初期的柔性管缆线型静态设计基于悬链线方程[5]进行,而且能够非常高效地求解柔性管缆的静态线型,但是悬链线方程忽略了柔性管缆的弯曲刚度,对柔性管缆曲率的估计会出现较大误差;随着有限元法[6]的发展,将其应用于柔性管缆线型静态设计数值求解,可以考虑弯曲刚度的影响,但是计算效率低;邹科[7]提出了考虑弯曲刚度的悬链线方程算法,能精确分析弯曲刚度对静态线型曲率的影响,对静态线型设计有重要意义。为提高柔性管缆整体线型设计效率,学者将数值优化方法引入柔性管缆线型设计中,优化模型采用忽略弯曲刚度的线型理论[8]或考虑弯曲刚度的线型理论[9],开展了多项相关工作。

综上,目前柔性管缆整体线型静态设计中,通常采用经典忽略弯曲刚度的悬链线理论方法;虽然部分学者引入了考虑弯曲刚度的悬链线理论应用时域分析方法进行动态分析,但有关考虑截面弯曲刚度对不同线型静态设计的影响研究相对较少[10-14]。为此,本文通过总结常用线型忽略截面弯曲刚度和考虑截面弯曲刚度的整体线型静态设计算法,开展弯曲刚度对常用线型静态设计的灵敏性分析,提高柔性管缆整体线型静态设计的效率和精度。

1 海洋柔性管缆整体线型静态设计理论

1.1 忽略截面弯曲刚度的悬链线理论

传统的悬链线型设计时忽略截面弯曲刚度,其线型直接由经典的悬链线方程控制,如图1所示悬链线最低点过坐标原点的悬链线方程可以表示为:

y=a(cosh(x/a)-1)

(1)

1.1.1 悬链线型静态设计方法

基于经典悬链线方程的推导,其中参数a可由悬挂点受到的水平张力Th与柔性管缆单位湿重ωs的比值表示,即a=Th/ωs。在静态线型设计时单位湿重ωs已知,悬挂点处张力的竖直分量Tv满足Tv=ωS,其中S是柔性管缆的长度,S可通过水深进行试算选取。

又因为悬链线上任意点的倾角θ满足:

tanθ=sinh(x/a)=S/a=Tv/Th

(2)

所以静态线型设计时可以使用水平张力Th或悬挂角度θ作为设计变量进行,也就是确定参数a。在参数a确定时,柔性管缆自由悬链线型的几何形态、张力和曲率也就随之确定,悬链线上的任意点曲率κ可以表示为:

(3)

悬链线的最小弯曲半径发生于x=0处,曲率κ=1/a=ωs/Th。

从原点到任意点的悬链线弧长为:

S=asinh(x/a)

(4)

悬链线方程确定时,基于可能发生的失效模式进行验证,选择合适的设计值。这一理论是求解忽略弯曲刚度整体线型的基础,可用于求解其他线型。

1.1.2 波型线型静态设计方法

波形线型是通过在悬链线中部适当位置上分布布置浮力模块(浮筒)改变线型几何形态,与波浪形态相似。波型线型由于缓存了一定的长度能够顺应较大的浮体偏移。依据柔性管缆末端在海床上的安装形式不同,可分为陡波线型和缓波线型,陡波线型有一个固定装置安装在柔性管缆底部,使得柔性管缆底部在竖直方向有一定的角度,缓波线型底部与水平方向夹角则为零,如图2所示。

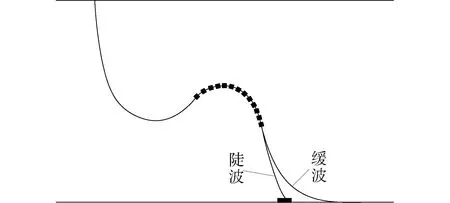
图2 波式线型

基于经典悬链线理论设计柔性管缆波形线型时可以采用角度控制线型几何形态,有直观、无量纲、参数独立等优点。波形线型可以视为由3段悬链线组成:上悬链线段(也称为垂弯段)、浮力段(也称为拱弯段)、下悬链线段。如图3所示,其中L1、L2、L3分别为上悬链段、浮力段、下悬链线段的长度;Wd为水深;ωs为柔性管缆湿重;ωb为等效合并后浮筒段单位长度浮力;Th为顶部悬挂点水平张力;X1、X2、X3分别为上悬链段、浮力段、下悬链线段水平投影长度;Z1、Z2、Z3分别为各段关键位置的高度。

3段悬链线型之间有2处连接点,在这2个连接点处张力相等、角度相同。采用角度为设计变量:顶端脱离角θ1,2个连接点处角度θ2、θ3。考虑到缓波线型和陡波线型仅在底端有区别,可将增加触地点的角度θ4为设计变量,将缓波线型和陡波线型设计归纳到一起,θ4=0表示缓波线型,0<θ4<90°表示陡波线型,设计过程如下。

顶端点处张力的竖直分量Tv为:

Tv=ωs(L1+L3)+ωbL2

(5)

顶端点脱离角θ1满足:

tanθ1=Tv/Th

(6)

得到顶端点处张力的水平分量Th为:

Th=Tvtanθ1

(7)

可得各段悬链线的湿重比分别为a1和a2：

L1和L3段的湿重比a1：

a1=Th/ωs

(8)

L2段的湿重比a2：

a2=Th/ωb

(9)

可以推导出系列方程用于求解缓波线型:

θ3=arctan(tanθ4+L3/a1)

(10)

θ2=arctan(L2-a2tanθ3)/a2

(11)

θ1=arctan(L1-a2tanθ2)/a1

(12)

基于经典悬链线方程,结合式(5)～(12),可以计算出水平投影长度X1、X2、X3,关键位置的高度Z1、Z2、Z3。

(13)

结合式(13)可以得到由角度设计法缓波线型从悬挂点到触底点的几何形态、张力及曲率。

1.1.3 S型线型静态设计方法

S型线型是通过安装浮拱将柔性管缆从形态上分为上、下悬链线段以及中水浮拱段。与波式相同,依据线型触地端在海床上的安装形式差别,可分为陡S式和缓S式。S型线型同样有较好的顺应性。但是,由于需要设计和安装中水浮拱,所以该线型的造价高、安装难度大。

S型线型设计时视作2段悬链线,如图4所示。其中集中式浮力附件(中水浮拱)通常具有足够大浮力,上部为固定曲率,可视作2段悬链线的端部固定点。

图4 S型线型的设计参数

同样,采用角度为设计变量:顶端脱离角θ1,2个连接点处角度θ2、角度θ3、触地点的角度θ4,θ4=0表示缓S线型,0<θ4<90°表示陡S线型,设计过程如下。

顶端点处张力的竖直分量Tv为:

Tv=ωs(L1+L3)+ωbL2

(14)

顶端点脱离角θ1满足:

tanθ1=Tv/Th

(15)

得到顶端点处张力的水平分量Th为:

Th=Tv/tanθ1

(16)

可得两段悬链线L1和L3的湿重比为a1：

a1=Th/ωs

(17)

L2段为固定曲率。

根据式(17)可得:

θ3=arctan(L3/a1)

(18)

L1段由方程y=a1(cosh(x/a1)-1)控制,其中有:

tanθ1=sinh(x1/a1)

(19)

tanθ2=sinh(x2/a1)

(20)

对于给定的θ1和θ2控制方程的x1段形态和x2段形态。

L3段由方程y=a1(cosh(x/a1)-1)控制,起点x4满足tanθ4=sinh(x4/a1);终点由x3控制,其中x3满足tanθ3=sinh(x3/a1),其设计过程可理解为从悬链线上截取一段进行平移变换到指定位置,这样S型线型由悬挂点到触底点的几何形态、曲率就随之确定,然后基于可能的失效模式进行验证,最后完成S型线型的静态设计。

1.2 考虑截面弯曲刚度的悬链线理论

虽然基于经典的悬链线方程可以非常高效地求解柔性管缆的静态线型,并且有较好的近似效果,但由于忽略柔性管缆截面的弯曲刚度的影响,在特定情况下对线型曲率的计算有较大误差,因此精确地分析考虑弯曲刚度下的悬链线最小弯曲半径对线型设计具有重要设计意义。邹科等[7]基于欧拉-伯努力梁模型推导了带刚度的悬链线方程满足的本构关系,精确地分析弯曲刚度对悬链线曲率的影响,推导结果如下。

考虑弯曲刚度的悬链线型模型如图5所示。

图5 考虑弯曲刚度的悬链线型模型

可以得到带刚度的悬链线微分方程组:

(21)

式(21)为考虑刚度的柔性管缆在自重、浮力和张力作用下形成的曲线在微段上必然满足的微分方程组。其中,柔性管缆的长度S,柔性管缆的湿重为ωs,弯曲刚度为EI,柔性管缆微元与水平线的夹角为θ,水平张力Th,柔性管缆的轴向张力为T,柔性管缆截面剪力为Q,求解此方程组可得到考虑弯曲刚度的悬链线线型。

这一理论也可用于求解考虑弯曲刚度的其他线型,以缓波线型为例,浮筒段受到垂直向上的均布作用力,其他段受到垂直向下的均布作用力,如图6所示。

图6 考虑弯曲刚度的缓波线型模型

将缓波线型分为3段,从左到右分别为下悬链线段、浮筒段、上悬链线段,对各段进行受力分析列平衡方程。

对比各段的方程,定义q(S)为湿重函数,下悬链线段q(S)满足:

q(S)=ωsS

(22)

浮筒段q(S)满足:

q(S)=ωbSf(S)-ωsS

(23)

式中Sf(S)表示浮筒段的长度。

上悬链线段q(S)满足:

q(S)=ωbSf-ωsS

(24)

可将缓波线型微分方程归纳为:

(25)

式(25)为考虑刚度的柔性管缆在自重、浮力、浮筒浮力和张力作用下形成的曲线在微段上满足的微分方程组。适用于线型中既有垂直向上的均布力,也有垂直向下的均布力的线型,即也可求解其他线型,如S线型也同样适用。

2 海洋柔性管缆静态线型设计截面弯曲刚度灵敏性分析

2.1 基本参数

本文以南海环境下某浮式风电动态海缆为例,研究不同水深情况下弯曲刚度对常用线型静态设计的影响,浮式风电动态海缆参数和水深参数[2,7,15-17]选择分别见表1和表2。

表1 浮式风电动态海缆参数

表2 水深选择参数

2.2 弯曲刚度对悬链线型静态设计的影响分析

基于上述静态线型设计理论,首先对不同水深悬链线型进行静态设计,水深选取:极浅水30 m、浅水100 m、半深水500 m、深水800 m和超深水1 600 m,研究弯曲刚度对线型静态设计的灵敏度。不同水深条件下线型与曲率的对比,结果如图7～11所示。

图7 30 m水深悬链线型对比

分别基于忽略弯曲刚度与线性弯曲刚度在极浅水30 m水深环境下进行悬链线型静态设计,其线型布置、曲率如图7(a)、(b)所示。可以看到柔性管缆静态设计基于经典悬链线法(忽略弯曲刚度)计算结果与考虑弯曲刚度算法计算结果有较大差距,尤其在触底点处基于经典悬链线法计算结果对曲率的估计误差在50%以上,此时弯曲刚度对悬链线型静态设计的影响较大,采用考虑弯曲刚度的算法进行静态设计更为合理。

水深为100 m时,基于经典悬链线法(忽略弯曲刚度)计算结果与考虑弯曲刚度算法计算结果如图8所示。此时线型布置、曲率结果仍有差距但较小,对曲率的估计也是触底点差距最大,在10%以内。

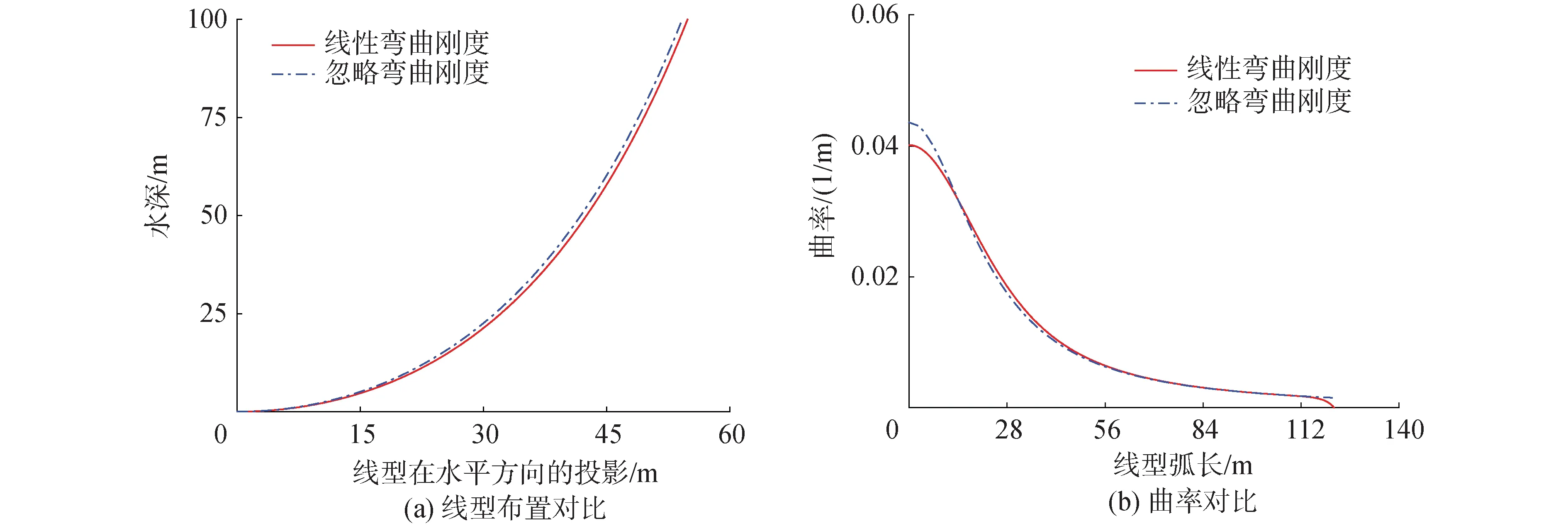
图8 100 m水深悬链线型对比

在半深水500 m以上,由图9～11可以看出,线型布置图和曲率图已经完全重叠,也就是此时弯曲刚度对悬链线型静态设计已经没有影响,可基于经典悬链线法进行快速静态设计。综合对比图7～11,可以发现在水深较深时,弯曲刚度对线型的曲率影响很小。而在水深比较浅时,柔性管缆的弯曲刚度对曲率计算的影响就较大,不考虑弯曲刚度的悬链线理论就存在较大的误差。由图7(b)极浅水环境下曲率对比可以发现忽略弯曲刚度算法计算得出的曲率比考虑弯曲刚度算法得出的曲率要大,也就是弯曲刚度对柔性管缆弯曲有一定的保护作用。由综合图12和表3在浅水柔性管缆线型设计时,考虑弯曲刚度使得线型设计空间更大,能得到更精确的设计结果。

表3 不同水深下忽略/线性弯曲刚度曲率计算结果对比

图9 500 m水深悬链线型对比

图10 800 m水深悬链线型对比

图11 1 600 m水深悬链线型对比

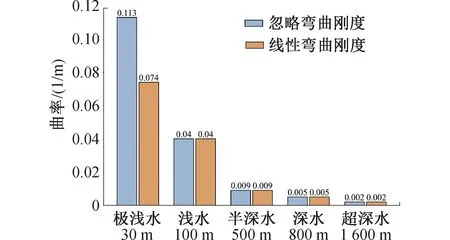
图12 不同水深悬链线型最大曲率对比

2.3 弯曲刚度对缓波线型静态设计的影响分析

同样,基于上述静态线型设计理论,对不同水深缓波线型进行静态设计,水深选取:极浅水30 m、浅水100 m、半深水500 m,研究弯曲刚度对缓波线型静态设计的灵敏度。不同水深条件下线型与曲率的对比,结果如图13～15所示。

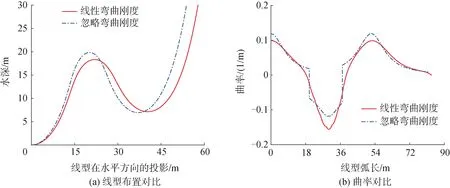
图13 30 m水深缓波线型对比

分别基于忽略弯曲刚度与线性弯曲刚度在极浅水30 m水深环境下进行缓波线型静态设计,其线型布置、曲率如图13(a)、(b)所示。可以看到柔性管缆静态设计基于经典悬链线法(忽略弯曲刚度)计算结果与考虑弯曲刚度算法计算结果有较大差距,和悬链线型不同,此时最大曲率差距在浮力段最高点处,基于经典悬链线法计算结果对曲率的估计误差在30%以上;由图13(b)可以看出,基于经典悬链线法对曲率计算的结果在图中各连接点处表现出跳跃的现象,不连续的原因是该算法计算时将缓波线型分为3段,在2个连接点边界处由斜率相等确定,即该点处一阶导数相同,但其二阶导数并不相同,导致曲率在连接点处不连续,对曲率的估计不准确。相比考虑弯曲刚度的算法曲率的计算结果为连续的,且更为精确。因此弯曲刚度对悬链线型静态设计的影响较大,采用考虑弯曲刚度的算法进行静态设计更为合理。

水深为100 m时,基于经典悬链线法(忽略弯曲刚度)计算结果与考虑弯曲刚度算法计算结果如图8、14所示。此时线型布置结果有差距但较小,曲率结果差距较大,对曲率的估计在浮力段最高点处,误差在50%以上。

当水深达到500 m时,缓波线型布置图已经完全重叠,但受到算法的影响,对曲率估计仍有较大的差距,误差在50%以上。在图15(b)中考虑弯曲刚度算法得出的曲率在缓波线型浮筒段出现“毛刺”的现象,这是由于此时缓波线型浮筒段长度较长,受到浮筒浮力的影响,浮筒处浮力较大,浮筒与浮筒之间的柔性管缆受到浮力较小,整个浮筒段的浮力分布并不均匀,出现曲率出现“毛刺”的现象。在水深较浅时,对比图13(b)、图14(b),这一现象并不明显,可以得到浮筒段的长度越长,其浮力分布不均匀越明显,对曲率的影响越大,从而浮筒段浮力不能简单等效成均匀分布,应当视为不均匀分布。由图13(b)、图14(b)、图15(b)、图16、表4曲率对比可以发现忽略弯曲刚度算法计算得出的曲率比考虑弯曲刚度算法得出的曲率要小,计算结果更保守,也就是采用考虑弯曲刚度算法进行缓波线型设计时的设计空间更大,提高了线型设计的可行性。水深在500 m以上时,缓波线型布置图已经完全重叠,且忽略弯曲刚度算法的计算结果更保守,因此也可基于经典悬链线法进行快速静态设计。

表4 不同水深下忽略/线性弯曲刚度曲率计算结果对比

图14 100 m水深缓波线型对比

图16 不同水深悬链线型最大曲率对比

3 结论

1)在浅水时忽略弯曲刚度的设计方法对曲率估计误差较大,不建议采用。

2)在深水时,弯曲刚度对线型静态设计影响甚微,因此可直接采用经典的悬链线法求解柔性管缆的静态线型。

3)缓波线型静态设计时,忽略弯曲刚度的算法得出的结果更保守,考虑弯曲刚度的算法得出的结果更精确,且有更大的设计空间,提高了线型设计的可行性。

4)受到浮筒浮力的影响,进行深水缓波线型分析时,其浮筒段浮力应当考虑其不均匀性。

所以,在线型静态设计时需基于不同水深进行不同方法选择,实现线型静态设计的高效性和精确性,本文工作也为基于静态分析结果结合动力放大系数的工程设计方法提供理论依据,从而提高整体线型设计效率。