信标信号的随机共振稳态跃变检测方法

万光明, 梁国龙,2,3, 王晋晋,2,3, 董文峰

(1.哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001; 2.海洋信息获取与安全工信部重点实验室(哈尔滨工程大学), 黑龙江 哈尔滨 150001;3.哈尔滨工程大学 水声技术全国重点实验室, 黑龙江 哈尔滨 150001 )

当飞机在海上失事后,为了能够在茫茫大海中尽快找到飞行数据记录器(即俗称的“黑匣子”),就要借助于其上安装的声信标[1]。声信标入水后即开始发射声脉冲信号以为黑匣子的搜寻提供帮助。通用的信标信号是一种单频脉冲信号,声源级低(约160.5 dB),频率高(约37.5 kHz),传播衰减快,脉宽窄(约10 ms),导致很难在远距离处实现信号检测。为获得更好的检测效果,本文研究了随机共振理论[2-4](stochastic resonance, SR),借助随机共振系统对微弱信号的增强效果,实现低信噪比下的信号检测。

随机共振一般是指在某一特定的非线性系统内,小参数周期信号激励与高斯白噪声之间产生了共振现象。当共振发生时,强噪声不但不会削弱信号,非线性系统在一定条件下可以将噪声能量向信号转移,使得系统输出信噪比提高[5-7]。经典双稳态系统的随机共振理论是在绝热近似条件下进行研究的,即存在一个小参数限制,这意味着信号频率应小于1 Hz。因此,经典随机共振无法直接检测高频信号。为了使随机共振更具实用性,研究人员提出了几种大参数随机共振方法,如变尺度频率随机共振[8-9]、系统参数归一化变换随机共振或参数归一化随机共振[10-11]、二次采样随机共振[12-13]。这些方法将大参数信号转换为满足小参数条件的小参数信号。这些方法的缺点是要求高采样频率(至少为信号频率的50倍,通常为100倍以上),当弱信号频率较高时,在工程应用场景中信号采集系统很难实现过高的采样频率,限制了这些方法的应用。调制随机共振[14-15]通过调制方式将高频信号调制为低频率信号,无需高采样率即可实现大参数随机共振,而该方法需要较长的信号持续时间,以确保持续时间包含至少2个完整的差频信号的周期,不适用于窄脉宽信号的检测。

针对上述问题,作者在先前的研究工作中提出了一种混频及归一化随机共振[16](mixing and normalizing stochastic resonance, MNSR)方法,该方法通过混频、滤波处理后得到较低频率的差频信号,再采用参数归一化方法实现差频信号的随机共振,可应用于处理黑匣子信标信号这类具有频率高、脉宽窄特点的信号以提高输出信噪比。信标信号这类单频信号在频域上表现为线谱形式,故常常采用频域上的能量检测方法进行检测判决[17]。当MNSR系统被设计为容易产生单频信号的随机共振时,若噪声在相近频点处的频率分量能量较高时容易出现虚警。本文提出稳态跃变适配次数作为检测统计量,基于MNSR系统输出波形的稳态跃变分布,在系统输出的时域上构建检测统计量——稳态跃变适配次数。通过调整势垒变换系数,使输入有信标信号与无信标信号时的输出波形表现出较大差异,即有信号时系统输出有更多的稳态跃变次数。通过计算机仿真和湖上实验,验证该方法在信标信号检测中可获得较频域能量检测更好的检测效果。

1 MNSR系统原理

随机共振方法是一种用于微弱特征信号增强检测方法,其不同于传统线性滤波方法的抑制噪声,而是通过构建一个非线性系统使周期信号和噪声达到共振。利用将噪声的部分能量转化为信号能量的机制来提高输出信噪比,提升检测性能。双稳态非线性系统在受到噪声n(t)与外部周期信号s(t)=Acos(2πft)作用时可以由郎之万方程(Langevin equation,LE)描述:

(1)

(2)

式中:噪声n(t)是均值为0,方差为σ2的高斯白噪声;设噪声强度为D,有σ2=2D;U(x)是非线性系统的势函数,a、b为势函数的势垒参数;x(t)是双稳态系统的输出,可通过四阶龙格库塔法求解LE得到,该方法表示为:

(3)

式中:h为计算步长,取值为采样间隔;si、ni、xi分别表示输入中的周期信号s(t)、噪声n(t)和系统输出x(t)采样序列中第i个点的值。

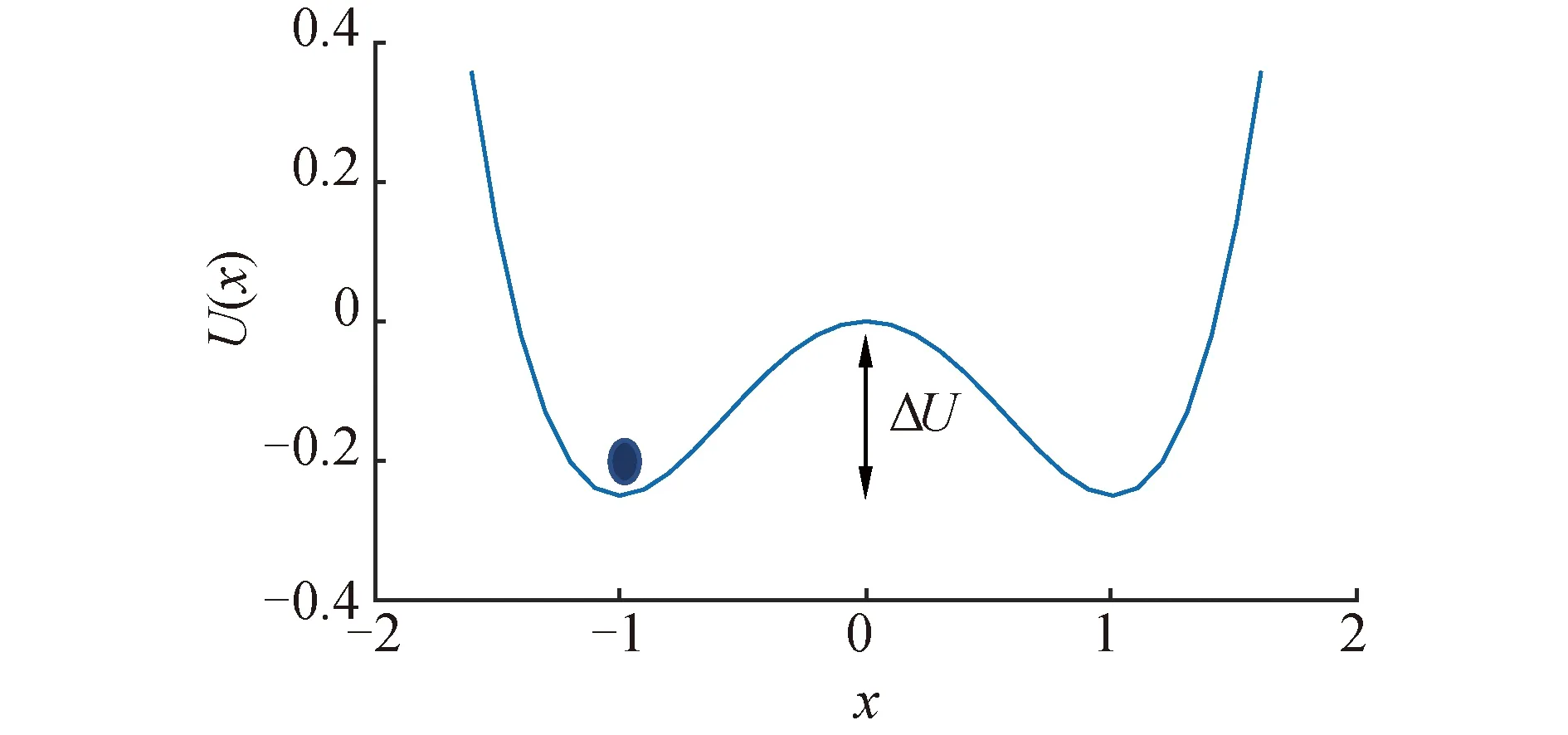
图1 双稳态系统的势函数 (a=b=1)

在先前的工作中作者提出一种适用于黑匣子信标信号这类高频、窄脉宽信号的大参数随机共振方法——混频及归一化随机共振(MNSR)。该方法通过混频处理获取差频信号满足随机共振方法的数值解法中对高采样倍数的要求[18],即采样频率需满足信号频率的50倍以上。MNSR检测方法通过对差频信号的检测来实现信标信号的检测,则采样频率不需高于信标信号频率(37.5 kHz)的50倍;而只需高于差频信号频率的50倍以上即可。由于脉宽限制,为保证脉宽时间10 ms内至少包含2个完整的周期信号波形,差频信号频率须高于200 Hz,在此基础上采用归一化随机共振方法解决了差频信号频率高于1 Hz情况下的大参数信号的随机共振。该方法的处理流程如图2。

图2 MNSR方法的处理流程

设混频器的本振信号为cos(2πfct),混频器输出经低通滤波器后输出信号为:

m(t)=A′cos(2πΔft)+n′(t)

(4)

式中:Δf=|fc-f|为差频信号的频率;n′(t)为高斯白噪声经滤波器后的输出,均值为0,方差为(σ′)2。

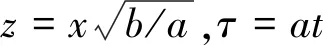
(5)

进一步简化后可得参数归一化后的随机共振的LE:

(6)

(7)

对于式(6),归一化双稳态随机共振系统的势垒参数ap=bp=1时,已知有多组输入信号参数可产生随机共振现象,如频率fp=0.1 Hz,噪声方差(σp)2=25。在工程上检测信标信号时,信号采集系统会设计有前置滤波器,这是考虑到信标信号频率通常分布在36.5～38.5 kHz,同时为去除过大的带外干扰。通过选取合理的势垒参数a、b使归一化后的频率fp,方差σp2变换为这些已知的归一化参数,可在归一化双稳态系统中产生随机共振现象。则MNSR系统的势垒参数a、b选取可按照:

a=Δf/fp

(8)

b=a3(σp/σ′)2

(9)

式中σ′可由滤波器的输出信号的方差近似求得。

图3为MNSR处理信标信号的仿真试验结果。其中,采样频率设为150 kHz, 输入的周期信号频率f=37.5 kHz,幅度A=0.5,脉宽T=10 ms;高斯白噪声方差为σ2,σ2=25。此时的接收信号的功率信噪比RSN=10lg(A2/2σ2)=-23 dB。取混频后的差频信号频率Δf= 1 000 Hz,则本振信号频率fc可取为38.5 kHz。此时采样频率相较于差频信号频率的采样倍数为150。MNSR的系统参数由式(8)与(9)计算得到:a=104,b=2.8×1014。图3(b)中微弱信标信号频点37.5 kHz的谱峰并不能在噪声背景下凸显出来,而在图3(d)中经过MNSR方法的处理,输出频谱在差频信号频点处即1 kHz处出现了尖锐谱峰,显著高于噪声背景,实现了信标信号的随机共振,增强了微弱信号的能量。

图3 MNSR的仿真结果

2 MNSR系统的稳态跃变检测器

2.1 基于稳态跃变分布的检测原理

在上文中知道随机共振现象的产生是系统粒子要借助噪声能量跨越势垒实现稳态间的跃变,对固定的带噪输入信号,可改变MNSR系统势垒高度ΔU使系统的稳态跃变分布出现变化。

当增加系统势垒高度,即增大参数a或减小参数b,系统粒子借助噪声能量实现跨越势垒的难度也随之增大,则输出波形的稳态跃变次数减少。由式(8)可知,参数a的选取与周期信号的频率有关,则固定参数a,通过改变参数b来改变势垒高度ΔU。设改变后的势垒参数为b′=b/w,其中w为势垒高度变换系数,为大于零的实数。随着系数w的增大,势垒高度ΔU′(ΔU′=w·ΔU)也增加,即通过调整系数w达到改变系统输出的稳态跃变分布的目的。

图4给出了变换系数w为1和50时的MNSR系统的输出波形。仿真噪声参数和信标信号参数同图3,令接收信号长度20 ms,其中前10 ms的输入为纯噪声n(t),后10 ms的输入是带噪信号m(t)=s(t)+n(t)。由图4可知,当变换系数w为1时,输入为纯噪声时(前10 ms)稳态跃变次数为17;有信标信号输入时(后10 ms)稳态跃变次数为18,二者差值为1,不易判断有无信标信号是否影响系统输出的稳态跃变次数。当变换系数w为50时,前10 ms的稳态跃变次数为9;后10 ms稳态跃变次数为14,二者差值为5,已出现明显差别。

图4 不同w时MNSR的输出波形

调整后的势垒高度ΔU′使MNSR输出的稳态跃变次数在有无信标时出现较大差异,可为检测信标信号提供了一种新的思路。当相邻过零点间距在半个差频信号周期长度左右时,可认为这2次正负稳态间的跃变得益于此时刻存在有差频信号,称之为稳态跃变适配。本文以过稳态跃变适配次数为检测统计量,构建基于稳态跃变分布的MNSR信标信号检测方法。

2.2 稳态跃适配次数检测器及其性能仿真

本文提出构建的基于稳态跃变分布的MNSR检测方法算法流程为:

1) 在信标信号脉宽时间内,记录MNSR输出波形上过零点的时刻t(1),t(2), …,t(n);

2) 计算相邻过零点间的时间间隔记为τ(k),τ(k)=t(k+1)-t(k),k=1, 2, … ,n-1;

3) 比较τ(k)与差频信号半周期长度T=1/(2×Δf); 当|τ(k)-T|<0.5T时,标记变量j(k)为1,否则置0;

基于稳态跃变适配次数N的检测判决式描述为:

(10)

式中:H0为无周期信号判决;H1为有周期信号判决;η判决门限,在奈曼皮尔逊准则下由虚警概率决定。综上,信标信号的检测方法的流程图如图5所示。

图5 信标信号的检测方法流程

在图3的仿真试验条件下,进行3 000次蒙特卡洛试验,给出统计量N在不同势垒高度变换系数w概率分布图:其中左侧虚线框柱状图对应的输入仅为纯噪声n(t);右侧实线框柱状图对应的输入为信标信号加噪声m(t)=s(t)+n(t)。

在图6中,随着系数w的改变4个图中左右柱状图重叠面积也随之改变,其中图6(b)～(d)的左右柱状图重叠面积均小于图6(a)。这说明不同系数w会影响稳态跃变适配次数N的概率分布,可通过系数w的优化选取获得更好的检测性能。根据图7绘制不同系数w下基于稳态跃变分布检测器的接收机工作特性(receiver operating characteristic,ROC)曲线,并与MNSR的频域能量检测器对比,结果如7所示。

图6 不同变换系数w时统计量N的概率分布

图7 不同系数w时稳态跃变适配次数检测与频域能量检测的ROC曲线对比

观察图7中的2条虚线,在变换系数w=1时,系统输出频域能量检测的ROC曲线位于输入信号频域能量检测的ROC曲线的上方,说明随机共振对信标信号的检测效果有提升作用;而基于稳态跃变适配次数的检测方法曲线(“□”标记曲线)与频域能量检测曲线(“▷”标记曲线)出现了交叉。这主要是由于MNSR的输入噪声为经过带通滤波器后得到的带限噪声,与信标信号的频率更加接近。当MNSR系统参数设计成易于实现系统粒子的稳态间跃变时,仅存在噪声时也会有较多的稳态跃变,只是这些跃变的频率不能稳定在某一频点处。此时通过统计稳态跃变次数进行判决则容易出现虚警。所以在较低势垒高度(w=1)时,采用频域能量作为检测统计量是更好的选择。

当增大系数w使其大于1时,可通过基于稳态跃变次数的检测方法获得更好的检测性能。在图7中,w=50、70、100的3条ROC曲线均位于频域能量检测曲线的上方;进一步观察,w=70时检测效果最好。

综上可知,通过势垒高度变换系数w的优选,基于稳态跃变适配次数的MNSR检测方法的性能优于基于频域能量的MNSR检测方法。

3 声信标探测实验数据验证

湖上实验于2021年10月在吉林市松花湖进行。在湖中通过锚系设备将黑匣子声信标置于水下20 m的深度,声信标自动以1.11 s周期向外发射37.5 kHz的声脉冲信号。接收水听器位于水下3 m,通过水密电缆连接到接收船上的电子舱中,对接收到的声信号进行采集处理。图8为接收船在距离声信标2.1 km处接收到的一个发射周期(1.11 s)声信标信号,其中信标信号地脉冲持续时间为0.77～0.78 s(图8(b)中虚线框中部分)。

图8 距离2.1 km处接收到的信标信号

利用MNSR方法对接收带信号进行处理,w=1时的MNSR势垒参数为a=104,b=8.5×1017,输出波形如图9所示。此时有无脉冲信号时间内的输出波形稳态跃变分布区分并不明显。

图9 w=1时MNSR处理结果

当系数w增大为50、70、100分别得到MNSR的处理结果,如图10所示。可知系数w越大,输出波形的稳态跃变次数就越少。这表明了本文引入的势垒高度变换系数w可以影响MNSR输出的稳态跃变分布。利用有无信标信号存在时系统输出波形的稳态跃变分布的差异性,构建基于跃变适配次数的MNSR信号检测方法具有可行性。

图10 不同势垒高度变换系数w时,MNSR的输出波形

图11是在20个信标信号发射周期内,分别使用基于稳态跃变适配次数的MNSR检测方法(w=70)和基于频域能量的MNSR检测方法的检测结果对比,其中横坐标为发射周期数,纵坐标为该周期内检测到信标信号的时延值;“□”标记表示的是基于稳态跃变适配次数的检测方法结果;“△”标记为基于频域能量的检测方法结果;水平虚线为信标信号的实际时延值。

图11 20个发射周期内2种方法的检测结果对比

在图11中,当检测到信标信号时的时延值在真值附近(5 ms内),可认为此次有信号的检测判决为准确判决;否则视为虚警判决。由图11可以发现,虽然2种方法都实现了20次的准确判决,但基于稳态跃变适配次数的MNSR方法检测结果中虚警次数(6次)明显少于基于频域能量检测的方法(20次),说明了基于稳态跃变适配次数的MNSR方法具有更良好的检测性能。

4 结论

1) 本文针对黑匣子探测应用场景下的信标信号的检测问题,提出一种基于稳态跃变分布的混频及参数归一化随机共振的信号检测方法。该方法均可实现类似黑匣子信号这种高频窄脉宽信号的微弱信号检测。

2) 设计了一个基于随机共振系统输出稳态跃变适配次数的检测器,通过调整势垒高度系数获得了较频域能量检测更好的检测性能,并通过湖上实验结果表明本文方法在实际工程场景中依然有效。

进一步地,如何在不同应用场景下选择最优的势垒高度变换系数是后续研究工作中的重点内容。