基于气动激励特征的压气机叶片高周疲劳分析

位景山, 郑群, 闫巍, 李赫飞, 王琦, 姜斌

(1.哈尔滨工程大学 动力与能源工程学院, 黑龙江 哈尔滨 150001; 2.中船重工集团公司第七〇三研究所 船舶与海洋工程动力系统国家工程实验室-海洋工程燃气轮机实验室, 黑龙江 哈尔滨 150078)

叶轮机械朝着高负荷、高推重比、高效率和低油耗的性能指标趋势发展[1],高速旋转叶片在离心载荷与气动载荷共同作下易产生较大的几何变形,使得流场的不稳定性和气动弹性问题更加突出,进而缩短叶片轴向间距,增强多排叶片工作中动静干涉,加剧叶片表面气动激励,从而引发高周疲劳甚至疲劳断裂等问题[2-3]。因此,需要深入研究压气机内动静干涉效应下,叶片表面非定常气动激励与振动及由此引发的叶片疲劳强度问题变得十分迫切。

叶轮机械叶片在气动载荷与离心载荷影响下的几何变形归于静态气动弹性力学(static aeroelasticity)问题[4-5],气动力在多级轴流压气机动静干涉下发生非定常变化,改变叶片变形量,使得气动性能发生偏移[6-8]。张帅等[9]针对流体与叶片之间强耦合问题,通过流固耦合方法对转子颤振现象进行分析,结果表明,考虑流固耦合作用的转子特性线发生偏移,并在最大效率点发生非失速颤振。Dong等[10]研究叶尖间隙对宽弦高速跨音速风扇转子气动弹性稳定性的影响,结果表明,随着叶尖间隙的增大,失速裕度和总压比减小,并改变局部流动,使非定常压力幅值和相位局部变化。Zheng等[11]通过实验与数值模拟方法对不同间隙下1.5级压气机叶片气动弹性振动问题进行研究,结果表明,叶片在不同间隙下的气动弹性稳定性主要受第一扭转模态的影响,叶尖涡强度和激波强度是影响转子气动弹性稳定性的关键因素。Naung等[12]使用直接数值模拟方法,探讨了现代LPT T106A涡轮的颤振和强迫响应机制,并研究了各种非定常源对叶片气动弹性失稳的影响。通过分析以上的研究发现,叶片的几何变形在径向改变叶间间隙,轴向加深动静干涉,改变非定常压力幅值与相位变化,使得气动性能发生偏移,从而对多级压气机整体性能产生更大的影响。

叶片气弹问题常见表现形式为强迫振动和颤振。颤振是叶片在气流中的耦合自激振动,激励与振动相互作用下短时间内振幅急剧增大,进而造成叶片破坏。强迫振动通常是由前排叶片尾迹或下游叶片的势扰动引起的,激励频率与转子转速和引起激励结构特征相关。由强迫振动引起的叶片高周疲劳问题严重限制了航空发动机结构的完整性和可靠性[13]。李润泽等[14]对压气机进行亚音速和跨音速2种工况下的数值模拟,通过对转子叶片表面非定常气动激励频谱及叶片强迫响应分析,得到跨音速工况下气动激励力特征和叶片强迫振动特性。马朝臣等[15]通过流固耦合对压气机叶轮的非定常气动力和叶片强迫振动进行计算,结果表明,当叶片处于共振频率时,非定常气动力导致叶片振动幅度增大。马艳红等[16]通过对模态频率与气动激励特征的不确定性分析,建立叶片概率疲劳损伤模型,得出叶片疲劳寿命可靠性。Juengst等[17]通过试验对跨音速压气机转子在近失速点的非定常流动引起的非同步叶片振动机理展开研究。Liu等[18]通过流固耦合方法研究了可调向心涡轮叶片表面压力波特性,结果表明导流叶产生的激波与叶尖间隙泄流导致压力波动,并诱发叶片谐振进而使叶片产成高周疲劳。张俊红等[19]考虑气动载荷和离心载荷作用下,求解叶片在复合载荷下的应力分布规律,结合疲劳试验,利用非线性连续损伤力学模型开展叶片在典型工况下的疲劳寿命研究。Ubulom等[20]通过解耦法和流固耦合计算方法对高压涡轮叶片的疲劳响应进行了预测,研究表明,流固耦合作用的影响会导致涡轮叶片疲劳性能和寿命评估的变化。

综上所述,现有压气机叶片振动及疲劳寿命研究多数是先进行流场分析,再将其作为外部激励施加于叶片有限元模型上,从而计算叶片在该瞬态气动载荷下的振动响应,没有考虑到流体诱发叶片振动导致高周疲劳问题是流体域与固体域相互耦合作用,无法精确分析非定常气动激励与叶片的振动特征对叶片高周疲劳的影响。

本文开展了压气机叶片在流体域与固体域相互耦合环境中气动激励对疲劳寿命研究。通过双向流固耦合数值模拟进行叶片在最高效率和近失速2个工况下的强度分析,研究气动激励引发叶片振动对叶片应力分布的影响,并根据疲劳强度理论建立叶片高周疲劳预测模型,进行了疲劳寿命预测。

1 计算模型及流固耦合数值方法

1.1 计算模型

本文所采用的计算模型为某型号船用燃机低压多级压气机的第1级,在前期工程应用中发现该压气机前面级设计转速下发生较为强烈振动,因此选择前1.5级为研究对象。压气机结构为进口导叶(IGV)、转子(R0)和定子(S0),叶片数分别为54、37和60。非定常计算采用约化算法[21],按照3∶2∶3的比例进行约化,得到的叶片数分别为54、36和54,使动静交界面两侧计算域具有相同的角度,保证周向非定常相位的一致性。约化后对转静轴向间距及动叶位置造成影响,从而影响到动叶通道中二次流与静叶尾迹在动叶通道中的耗散。对动叶片的优化,会造成转子通过频率的改变,静叶片优化会影响对动叶片的势干扰,但不会影响到转静干涉频率。压气机气动参数的时均值影响的量级不超过1%。流体域与固体域网格模型如图1所示。使用NUMECA的Autogrid5设置结构化网格拓扑。主流区网格拓扑为O4H,叶尖间隙采用蝶形网格。第1层网格距壁面为1×10-5m量级,对叶根和叶尖、前缘和尾缘、叶角和叶尖间隙的网格进行了精确的密集处理。IGV域沿轴向向上游扩展了2个导叶弦长,而S0域沿轴向向下游扩展了1.5倍定子弦长。每个叶片通道内进口导叶(IGV)区域、转子(R0)区域和定子(S0)区域的节点总数约63万网格节点。固体域R0叶片有限元模型采用非结构六面体单元,网格节点数为17万。叶片材料[22]密度7 850 kg/m3,弹性模量200 GPa,泊松比0.3。

在数值模拟中,使用稳态计算来验证网格的独立性。压气机的绝热效率和总压比随网格数的关系如图2所示。当单通道网格数超过60万时,绝热效率和总压比随网格数波动的变化小于0.2%。考虑到双向流固耦合的计算时间,选择了63万网格进行非定常数值模拟。

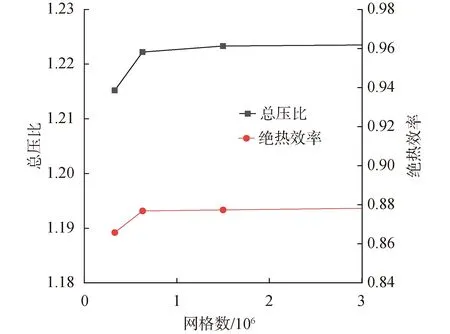
图2 网格模型的独立性验证

1.2 双向流固耦合设置

选用ANSYS CFX商业程序Navier-Stokes方程进行流场分析,使用自动时间尺度控制方法加快收敛速度,湍流模型使用k-ε模型,壁面函数使用Scalable。在进行非定常流场计算之前,使用定常计算结果作为非定常流场计算初始文件,将叶片旋转通过一个转子叶片节距物理时间步设置为10步,每步时间为1.75×10-5s,总步长为5.25×10-2s。进口总压和总温分别为101 325 Pa和288.15 K,设定轴向进气方向和低湍流度1%,通过改变出口静压模拟节流,采用径向平衡方程来保证压力分布,转子域给定旋转速度9 515 r/min。此外,在稳态模拟中将动静界面设为Stage (mixing-plane),在非稳态模拟中将动静界面设为transient rotor-stator,以保证上下游流动的连续性。固体域对叶片根部施加固定约束,转速与时间步长均与流体域一致。

以WORKBENCH为平台,设置流体叶片表面与固体叶片表面相应耦合fluid solid interface(FSI),如3所示。通过System Coupling模块进行CFX与Transient Structural数据传递,采用非匹配网格[23]实现流场域与固体域之间非定常压力和模型网格变形信息交换,对每一个时间步的叶尖位置位移进行监测,在一个物理时间步内监测点的最大位移随内时间步迭代的变化小于1×10-5m时,即认为达到了变形后的平衡位置。当流场域与固体域的压力与变形都达到收敛标准时,再进入下一步计算,详细流程如图4所示。通过双向流固耦合精确分析非定常气动激励下流体域与固体域相互耦合作用对叶片高周疲劳的影响。

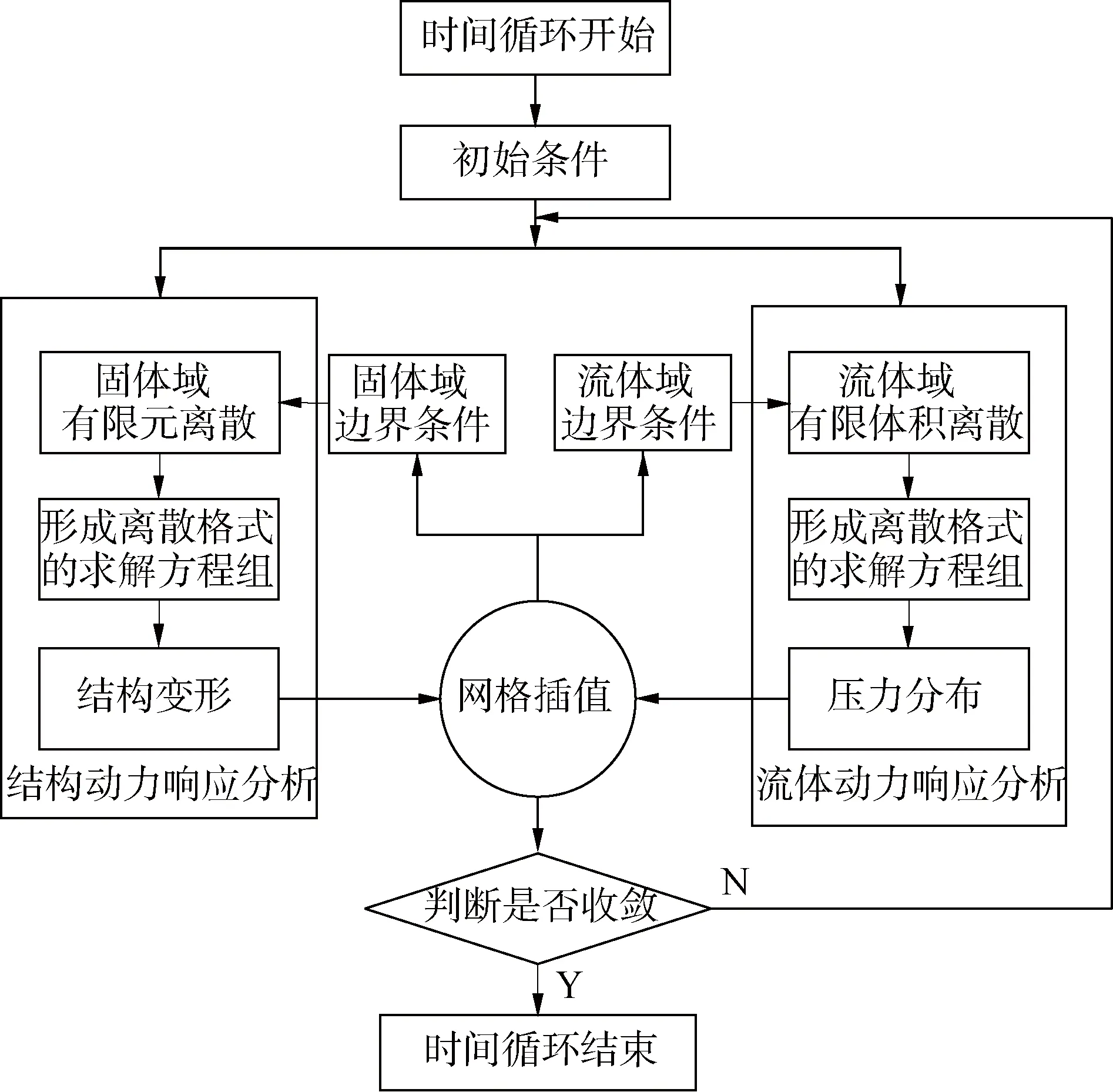
图4 流固耦合流程

2 叶片非定常气动激励分析

2.1 叶片非定常气动载荷时域分析

压气机特性线工况从101 325～115 000 Pa。每次增加1 000 Pa。在靠近失速边界时,背压每次增加100 Pa。直到压气机进入近失速状态。对压气机叶片最高效率点(出口背压为113 400 Pa)和近失速点(出口背压为115 600 Pa)2个工况进行数值模拟。通过与最高效率点为参考和对比,由于工程中一般以工作点作为设计点,而本文仅侧重于压气机机理研究,因此选择最大效率点代替设计点。研究近失速点气动激励引发叶片振动对叶片应力分布的影响,并开展叶片高周疲劳寿命预测。图5为2种工况下叶片非定常气动力的受力示意图对比。由图5可知,最好效率点流场流动均匀,两叶片所受气动力相一致。近失速点时两叶片80%以上气动力相差较大,这是因为近失速时所产生的二次流和叶顶泄漏流作用在叶片上,引起流动不稳定。

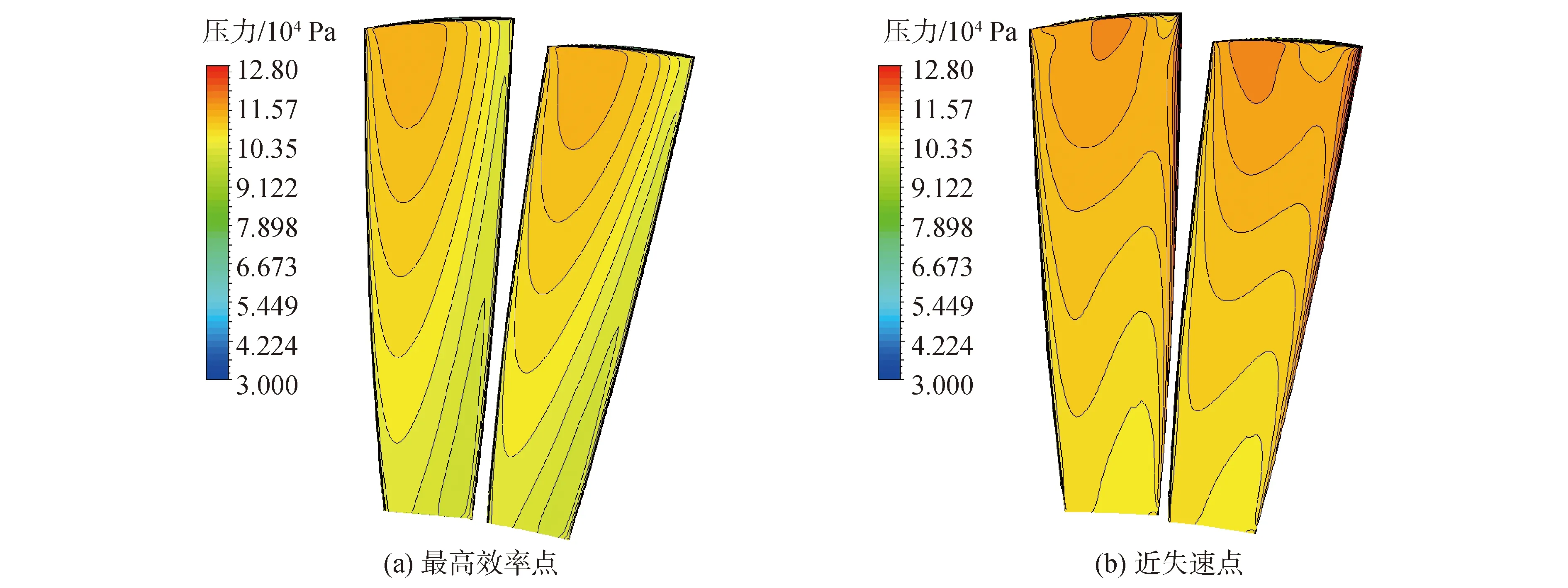
图5 2种工况下叶片的受力

图6和图7分别为最高效率和近失速2个工况点,转子叶片30%与90%叶高截面冷热叶型表面静压分布对比,其中“冷态叶片”为只考虑气动载荷不考虑叶片变形的非定常模拟结果,“热态叶片”是在气动载荷和离心载荷共同作用变形后的双向流固耦合模拟结果[24]。静气动弹性变形对叶片表面静压分布有较大影响。30%叶高截面冷态和热态叶片表面静压变化较小,而90%叶高截面2种叶型表面静压分布相差较大,其中叶片前缘静压差大于尾缘静压差。随着叶高的增加,静气动弹性变形对气动性能的影响不断增大,使得叶片上半部表面静压分布差异明显,同时,最高效率点处的静压分布和冷热叶型静压差均高于近失速点。

图6 最高效率点不同叶高静压对比

图7 失速点不同叶高处静压对比

在压气机中,很多因素会导致叶片振动,其中最主要的因素是流体作用在叶片上的扰动,而发动机稳定工作后,由于来流的变化相对规律以及叶片本身的转动,叶片会承受周期性的振动应力,也称为气动激振力F：

(1)

式中:A为叶片表面积;p为叶片表面受到的气动力。

通过双向流固耦合与非定常流场进行数值模拟,得到2种状态下转子叶片表面气动激振力,图8为最高效率点与近失速点4个周期内转子冷热态叶片气动激振力随时间的变化规律,由图8可知,热态叶片气动激振力在2个工况点均高于冷态叶片。在最高效率点时,转子叶片所受的气动激振力均呈现一定的周期性,但是热态叶片整体出现新的周期性波动,这是因为在流固耦合作用下,气动激振力作用在叶片上,引起叶片振动,同时叶片振动作用在流场中,使得流场产生新的波动。近失速点的气动激振力整体低于最高效率点,并且呈现非线性的波动,这是因为在近失速时,流场已经发生恶化,出现叶尖泄漏流,二次流等不稳定现象,叶片振动对流场的影响无法通过时域分析得出,因此需要对叶片表面气动激振力的特性进行频域分析。

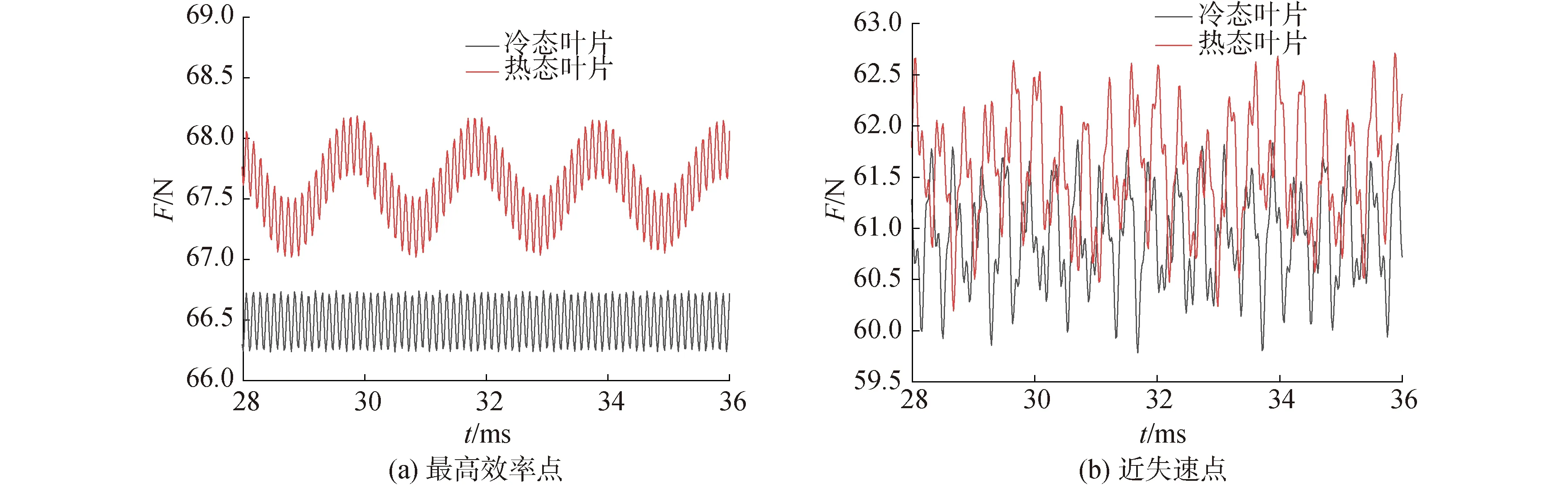
图8 叶片非定常气动力的时域分布

2.2 叶片非定常气动载荷频域分析

为了进一步分析叶片表面气动激振力的特性,通过傅里叶变换公式对其进行频域分析。压气机叶片在稳定运行工况下,转子叶片和IGV在相对运动过程中,由于尾迹效应在IGV出口处产生不均匀流场,同时转子叶片在气动力载荷作用下产生的周期性运动,将会产生有规律的、周期性的叶栅干扰。

傅里叶变换公式为:

(2)

傅里叶变换实质是时域转化为频域函数的过程,将原来关于时间t的时域函数f(t)转变为频率ω的频域函数F(ω)。

动静干涉频率:

fv=Z×n/60

(3)

式中:fv为转静干涉脉动频率;Z为IGV数量;n为转子转速。

图9给出转子叶片在2个工况点,冷态叶片和热态叶片气动激振力的频域分布。由图9可知,在2个工况点热态叶片上的扰动频率主要为叶片振动频率(492 Hz)和动静干涉频率(8 604 Hz)。冷态叶片的扰动频率幅度低于热态叶片,说明叶片静气弹性作用下叶排上半部分之间非定常气动干涉增强。而热态叶片气动激振力与冷态相比,出现新的谐波(492、1 682和2 230 Hz),与叶片前3阶模态频率相近,这是因为叶片振动扰动流场流动,使非定常气动力出现新的频率。相比于最高效率点,近失速点冷热态叶片气动激振力均出现3个新的谐波,分别是2 553 Hz为转子16倍频、3 428 Hz为22倍频和5 703 Hz为36倍频。结合图5和图8,产生3个新的谐波的原因主要是压气机工况接近失速时,流场中出现二次流,叶尖泄漏流等自身流场中非定常因素的影响,使得气动激振力的波动与最高效率点相比更加复杂。压气机叶片应力大小和分布,除受离心载荷和气动载荷外,还与叶片结构紧密相关。因此要了解压气机叶片在离心载荷和气动载荷作用下的应力分布,还要进一步进行强度分析。

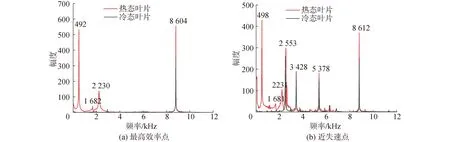
图9 叶片非定常气动激励的频域分析

3 叶片疲劳寿命分析

3.1 叶片模态与振动分析

图10为叶片1～6阶的固有频率振型。高速旋转下叶片刚度会发生变化,从而改变叶片振动频率。表1为叶片在不同载荷下的前6阶振动频率,其中ω1是叶片的固有频率;ω2是考虑离心载荷的振动频率;ω3是气动载荷与离心载荷共同作用下的振动频率;Δ是ω2相对ω1的增量。由表可知,离心载荷对叶片振动频率有较大影响,特别是对于低阶频率,第1阶振动频率提升16.36%,第3～6阶均在1%左右。考虑气动载荷对叶片结构作用后,第1和第2 阶频率增大,第3～6阶模态频率减小。在不同载荷下叶片固有特性有明显差异,在实际工程设计中,应考虑气动载荷与叶片结构的流固耦合作用能更加接近工程实际,提高计算的可靠性。

表1 不同载荷下叶片固有频率对比

图10 叶片前6阶振型

根据气动载荷与离心载荷共同作用下绘制坎贝尔图,如图11所示。当气动激振力频率与叶片固有频率成以下关系时,叶片可能发生共振或谐振,即:

fi=kfe

(4)

式中:fi为叶片某阶振动频率;fe为激振力频率;k为结构谐波频率。当k=1时发生共振,当k≠1时发生谐振。在同样激振力条件下,发生谐振的叶片振动幅度和振动应力都小于共振时,且随着k值的增加而降低。

在图11中,不同叶片模态频率线为图中横线所示,不同阶次谐波激励线为图中斜线所示。坎贝尔图中倍频线与压气机进口导叶数和下游静叶及流场气流分布不均匀等引起的倍频。激振频率与模态频率交点为共振点,对应的转速为共振转速。在进行压气机设计时,叶片工作转速要远离共振频率10%以上[25],为图中红色竖线。本文研究需考虑的谐波激励因子主要包括以下几类:k=54(导叶数);k=36(转子数);k=22和k=16(近失速时出现的新谐波);转子叶片前六阶低频激励。

由图11可知k=1和k=2与叶片第1阶频率没有交点,k=3,4,5,6与第1阶频率频率交点在10 813、7 429、5 621、4 704 r/min均在共振裕度以外。k=16、22、36、54与第1阶频率线交点在低速区,可以不予考虑。k=16与第3阶频率线相交于转速8 786 r/min,共振裕度为7.7%。k=22与第4阶频率线相交于转速8 977 r/min,共振裕度为5.7%;k=36与第6阶频率线相交,转速9 018 r/min,共振裕度为5.2%,对应的激振倍频是转子通过频率;k=54于第7阶和第8阶分别交于9 060和9 855 r/min,共振裕度分别为4.8%和3.6%,对应的激振倍频是动静干涉频率。k=16,22,36,54在工作转速裕度内分别与多阶模态频率相交,因此转子叶片在设计工况范围内工作时会发生不同程度的谐振,振幅较小,但会对叶片造成疲劳损伤,对叶片进行高周疲劳分析中应予考虑。

3.2 叶片位移分析

表2分别为气动载荷(aerodynamic load, AL)、离心载荷(centrifugal load, CL)、单向流固耦合(unidirectional fluid-structure interaction,UFSI)和双向流固耦合(bidirectional fluid-structure interaction, BFSI)4种载荷模拟情况下,叶尖前缘最大位移幅值及径向、周向和轴向位移分量的绝对值对比结果。双向流固耦合较单向耦合叶片最大位移量增大约7.1%。其中,周向位移分量最大(0.368 47 mm),其次为轴向位移分量,径向位移分量最小。通过气动载荷与离心载荷位移量对比,气动载荷导致的叶片位移量约占总位移量的24.063%,说明离心载荷对叶片的静气动弹性变形起主要作用。

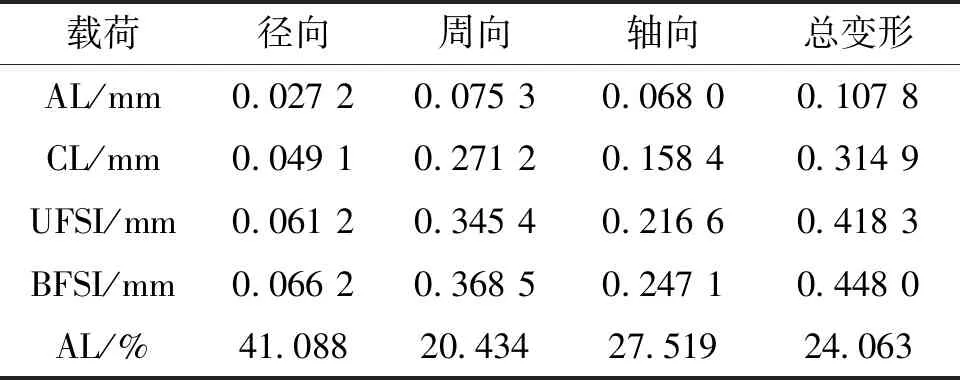
表2 不同载荷下叶片位移量最大值

转子叶片在4种不同载荷情况下位移云图如图12所示。

图12 不同载荷下叶片位移分布云图

由图12可知,离心载荷作用下叶片发生扭转变形,与叶片第3阶扭转模态振型类似,最大位移量出现在前缘叶尖,在叶片尾缘50%以上区域也出现较大位移。气动载荷和流固耦合下叶片发生弯曲变形,类似于叶片第一阶弯曲模态振型。叶片位移量整体趋势从尾缘叶根到前缘叶尖逐渐增大,在叶尖前缘处达到最大位移。叶片的轴向位移缩短了转子与导叶和定子之间的距离,使得多叶排间非定常流体激励干涉增强。叶片的径向位移使得实际工作状态的叶尖间隙和设计值有所不同,叶尖前缘径向最大位移量为0.066 mm,叶尖间隙始终小于设计值0.5 mm,保证了叶片变形后不与机匣发生摩擦,工程中压气机叶片设计应考虑径向变形量对叶尖间隙的影响。

转子叶片总位移中气动载荷引起的位移量约占24.063%,在非定常气动激励作用下转子叶片随时间发生周期性位移。为了研究非定常气动激励下叶片瞬态动力学响应幅频特性,对非定常气动激励作用下2个工况点叶尖前缘位移进行频谱分析,如图13所示。在非定常气动激励的影响下,叶片振动响应对应频率为第1阶模态频率,次谐波峰值很低,说明转子叶片以低频振动为主,同时第1阶模态频率在近失速点峰值最高效率点高于峰值,说明在近失速点非定常激动对叶片振动扰动程度更大。

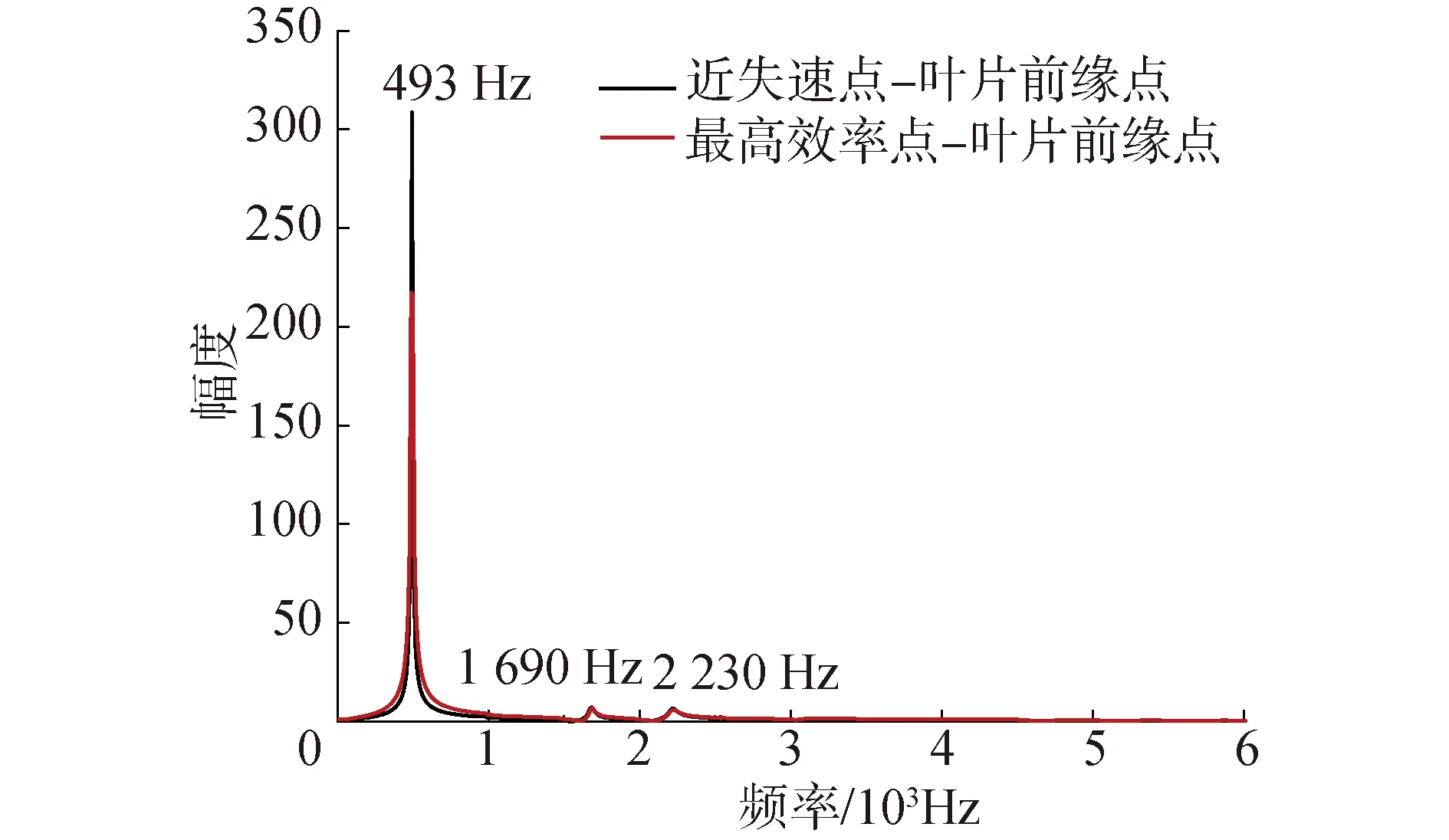
图13 前缘叶尖总位移幅值频谱图

通过图9和图13给出的流场气动激振力和叶片前缘位移响应两者的频域分析可知,在最高效率点时,冷态叶片仅出现一个频率(8 604 Hz)为动静干涉频率。在近失速点时,冷态叶片所受到的扰动中,动静干涉频率幅值最大,所以在流场中冷态叶片表面气动激振力频率主要来自动静干涉频率,且冷态叶片气动激振力波动峰值与热态叶片相比较低。热态叶片振动变形对流场非定常气动力产生影响,气动激振力频谱谐波发生改变,出现新谐波(492和498 Hz),与叶片一阶模态频率相近,结合图10和图12,叶片形变以弯曲变形为主,说明在该工况下叶片一阶弯曲振动更容易被激发。

3.3 叶片应力分析

对于叶片的疲劳失效分析,叶片的应力响应是重要参数,图14为非定常气动激励下最高效率点和近失速点叶片的等效应力云图。

由图14可知,应力最大值均位于压力面靠近前缘叶根区,这是因为气流激励下的叶片前缘顶部出现较大变形,前缘叶根由于轮毂的约束,变形受限,故而在叶根前缘附近产生较大应力,疲劳破坏多产生于最大应力处。近失速点的应力值为258.86 MPa大于最高效率点253.03 MP,这是因为在近失速点时,非定常气动激励出现新的谐波(2 553 Hz为转子16倍频、3 426 Hz为22倍频和5 378 Hz为36倍频,即转子通过频率),k=16、22和36倍频在工作转速裕度内分别与多阶模态频率相交,因此转子叶片在设计工况范围内工作时伴随谐振,振幅虽小,但也会增大应力。虽然最大应力没有达到材料屈服极限,但是在交变载荷作用下,叶轮可能发生高周疲劳失效现象。

3.4 叶片高周疲劳预估

由于压气机叶片真实运行环境难以实现,因此,基于设计的压气机叶片仿真模拟,开展气动激励引发叶片耦合振动的疲劳寿命预测。在工程设计时,通过材料S-N曲线预测结构疲劳寿命[26],叶轮机械的疲劳强度幅值与平均应力有关,Soderberg、Goodman和Yieid等模型是常用的平均应力修正模型。本文采用最保守Soderberg直线建立叶片高周疲劳预测模型,进行疲劳寿命预测[18]：

σa=σf(1-σm/σs)

(5)

式中:σa为对称循环疲劳幅值;σf为对称循环疲劳极限;σm为叶片总体应力水平;σs为屈服极限强度,σs=460 MPa[22]。

图15为叶片在不同工况下的叶片高周疲劳寿命云图。由图15可知,2个工况下叶片最小高周疲劳寿命值均位于压力面靠近前缘叶根区,叶片在最高效率时最大应力253.03 MPa,最小疲劳寿命为192 710 cycles;近失速时叶片最大应力258.86 MPa,最小疲劳寿命为173 460 cycles。近失速时比最高效率点应力增加2.3%,疲劳寿命降低11.1%。

图15 各工况下叶片疲劳寿命云图

综上分析,多叶排间动静干涉下,非定常气动激励引起叶片一阶耦合振动和近失速时多阶高倍频诱导叶片在工作转速裕度内产生高阶谐振,产生较大应力,从而降低叶片疲劳寿命,使得叶片更容易发生疲劳失效,难以保证叶片长时间安全可靠地运行。因此在压气机转子叶片结构设计阶段,有必要开展在流体域与固体域相互耦合环境中,气动激励诱发叶片耦合振动和谐振对疲劳寿命分析,并开展载荷与结构优化设计。

4 结论

1)最高效率点处的叶片气动激振力强度高于近失速点,但是近失速时流场中非定常因素的影响更加显著,产生多个高频谐波,易诱发叶片在转速裕度内发生谐振。

2)热态叶片振动变形对流场非定常气动力产生影响,气动激振力频谱谐波发生改变,出现与叶片一阶模态频率相近的新谐波,使得叶片更易激发一阶弯曲振动。

3)多叶排间动静干涉下,非定常气动激励引起叶片一阶耦合振动和近失速时多阶高倍频诱导叶片在工作转速裕度内产生高阶谐振,近失速时比最高效率点应力增加2.3%,疲劳寿命降低11.1%,该工况下容易造成叶片前缘叶根疲劳断裂。

本文只对亚音速压气机进行研究,并未对流场环境更复杂的跨音速和超音速压气机进行研究。后续考虑进口畸变,叶尖泄漏流、二次流和相对超音来流条件下的激波及激波/附面层干扰等因素下,进一步探索气动激励特性对叶片振动和高周疲劳的影响。