随机波列中极端波浪波形和波高分布的数值试验研究

夏维达, 马玉祥, 董国海

(大连理工大学 海岸与近海工程国家重点实验室,辽宁 大连 116024)

极端波浪是波高显著高于背景波浪的大波,由极端波浪引发的海洋事故每年都会造成巨大的经济损失和严重的人员伤亡。极端波浪具有波高大、非线性强等特点,并且出现之前无明显征兆,因此会对海洋结构物和船舶的航行安全造成巨大威胁[1-3]。对其的研究虽然已有几十年,但是目前对极端波浪生成和特性的研究仍然是学界的研究热点[4-9];波浪波高分布和极端波浪波形的研究对工程设计也有重要的意义。在一般的海洋结构物设计中,通常采用斯托克斯波为设计波浪,波高根据长期的水文数据确定;但是实际的海洋环境复杂,波浪为随机过程,所以为了更精确地计算结构物响应,通常需要长时间的模拟。Boccotti[10]和Tromans等[11]经过严密的理论推导,给出了随机波列中最可能出现的极端波波群的波面表达式,也叫新波模型(new wave model),为海洋结构物设计计算提供了新的思路。该模型的有效性也得到了验证[12-15]。之后Walker等[12]在新波模型的基础上加入了非线性项,并验证表明非线性修正后的模型能够较好地符合海洋中实测极端波浪的波形。Santo等[14]也研究了墨西哥湾飓风下观测到的极端波浪,并与新波模型进行了对比,发现实测的波浪具有更加明显的垂直不对称性并且具有明显的三维传播特征。Whittaker等[13]后来也通过实测数据验证了包含二阶非线性的新波模型在浅水条件的适用性。极端波浪的波形特征在波浪与结构物相互作用的研究中也至关重要。Slunyaev等[16]运用数值方法,模拟了随机波浪的传播,将波浪形态的分为前峰波、后峰波、前谷波和后谷波4类,发现大部分极端波浪的波峰后的波谷相对峰前的波谷要更深。Sergeeva等[17]也发现了类似的结果。Ma等[18]通过模型实验研究了逆流对规则波列中由调制不稳定性导致的畸形波的波陡、波形的不对称性的影响,发现逆流的存在会改变畸形波的不对称性。

随机波浪的波高分布在工程设计中具有重要的作用。Longuet-Higgins[19]对有效波高、平均波高和极大波高的关系做了系统性的研究,并给出了窄谱下的最大波高分布。Longuet-Higgins[20]接着在线性波浪模型下推导出了波浪波高服从Rayleigh分布;Kinsman[21]在现场观测中发现偏态会导致波面分布不再服从正态分布,于是他拟合出一种更符合实测数据的波面分布。Tayfun等[22]和Forristall[23]在考虑了二阶非线性后各自提出了二阶的波峰分布。但是二阶Tayfun分布和Forristall分布只考虑了约束波对波峰分布的影响,并没有考虑自由波共振作用的影响。Mori等[6,24]在窄谱的假定下,将波面高程概率密度函数用Edgeworth级数展开后,提出了MER分布。Tayfun等[25]同样考虑了四阶近似共振对波峰分布的影响,推导出了三阶Tayfun分布。这些波高分布模型都不是完美或者适用于所有工况的,需要根据实际情况和实际观测数据选择合适的波高分布模型。本文通过数值模拟多组不同工况下随机波的演化,对极端波浪的平均波形做了研究,验证了新波模型的有效性;最后对比了实验数据的波高,波峰分布与各种理论分布(Rayleigh分布、MER分布、Forristall分布和Tayfun分布等),探讨各种分布的适用性。本文中极端波浪的标准为波峰ηc/Hs>1.25的波浪或波高H/Hs>2.0的波浪。

1 数值模型及波浪参数

1.1 数值模型介绍

本文数值模拟采用的模型是高阶谱模型,由Dommermuth等[26]和West等[27]提出,能够满足完全非线性自由表面条件。该模型可以模拟任意阶数的波浪非线性传播和相互作用。高阶谱方法的优点是收敛性好、计算速度快、精度高;并且不受水深、谱宽等的限制。对于不可压缩的无粘无旋理想流体,引入自由水面处的速度势函数:Φs(x,y,t) =Φ(x,y,η,t),将其代入到自由表面边界条件中,则自由表面条件可表达为:

(1)

(2)

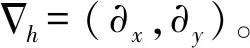
(3)

式中:w(m)和Φ(m)分别表示m阶的垂向速度和速度势;Φ(m)可以通过伪谱方法求解速度势的初边值问题得到。将式(3)代入式(1)和(2)便得到了波面升高η和表面速度势Φs的演化方程。演化方程可以通过四阶龙格库塔法进行求解。为了模拟造波边界,同时引入了附加速度势模拟造波板的运动,造波边界条件精确到二阶非线性。同样也加入了吸收边界来减少波浪的反射,吸收边界的实现采用对式(1)加入压力项[28],使得波面升高衰减。

1.2 波浪参数

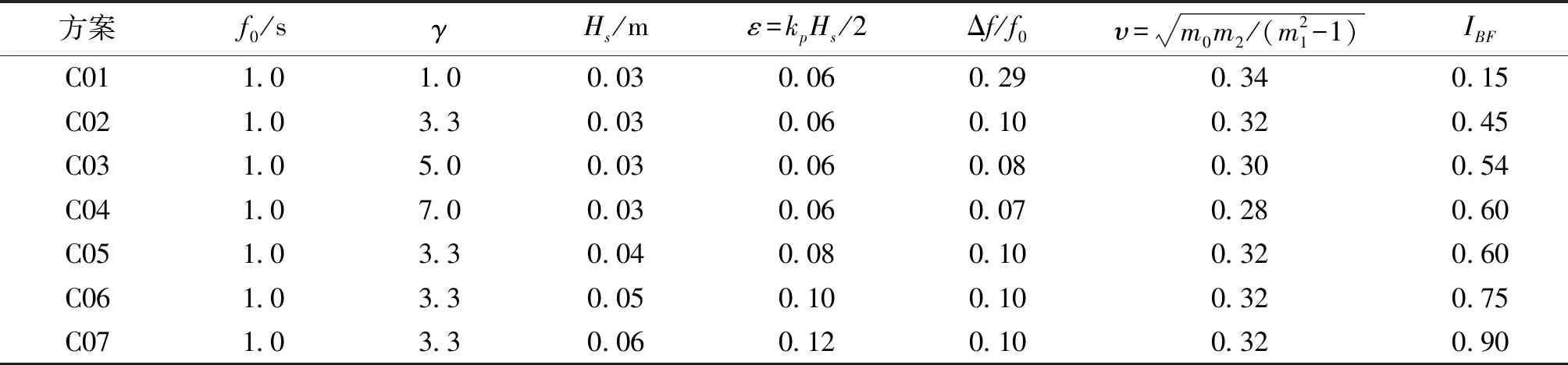
表1 波浪参数

2 结果与讨论

2.1 极端波浪平均波形特征与新波模型的对比

新波模型基于线性理论,没有谱宽的限制,可以描述极端波浪的平均波形;并且理论上平均波形也是最有可能出现的极端波浪波形。新波模型波面函数正比于随机过程的自相关函数,其表达式为:

(4)

式中:α为波峰高度;S(ω)为波浪场的谱密度函数;σ为波浪的标准差。Lindgren推导出了极端波浪波峰附近波面的方差,也称为Lindgren方差[30],其表达式为:

(5)

Walker[12]基于斯托克斯波展开式,在线性新波理论的基础上加入了非线性项,三阶非线性新波模型表达式为:

(6)

式中:ηLH为希尔伯特变换后的线性新波波面;h为水深;S22和S33取值参考Walker[12]中的方法。

为了研究极端波浪的波形特征,分别从6组数值模拟工况中提取出所有波峰高度满足ηc/Hs>1.25的波浪,并对波面进行平均,然后与三阶新波模型进行对比。图1为有效波高相同(Hs=0.03 m),谱宽依次减小的4组工况C01(γ=1.0),C02(γ=3.3),C03(γ=5.0)和C04(γ=7.0)模拟得到的极端波浪平均波形与三阶修正新波模型的对比图;图中实线为极端波浪波面平均后的结果,短线为新波模型波面;灰色区间为新波模型理论平均波面95%置信区间的范围;置信区间范围的上下限为η±2σE;其中σE为波面均值分布的标准差,也就是均值的标准误差;σE=(σL/N)0.5;N为极端波浪个数,每个工况的极端波浪个数在200左右。图中时间横坐标和空间纵坐标分别以谱峰周期Tp和有效波高Hs做了无因次化处理,并且都将极端波浪波峰时刻作为原点。从对比结果可以看到新波模型与数值模拟结果吻合较好,并且平均波形都在三阶新波模型95%置信区间的范围内;但是对于谱宽最宽的工况C01,波峰两侧的波谷位置处,三阶新波模型预测的波谷值较大;而对于其余工况,误差主要出现在极端波浪生成之前,波浪周期相对新波模型更短,波高也更小。从图中可以看到4组不同谱宽工况下三阶新波模型均能够较好地描述极端波浪的波形特征,但是对于窄谱,误差相对更小。从图1中还可以看到随着谱宽的减小,无因次波峰高度明显增大;4组工况平均后的波峰高度与有效波高的比值ηc/Hs分别为:1.38、1.39、1.43、1.44、并且波谷也随着谱宽的减小而增大;表明谱宽会影响极端波浪的波高,谱宽越窄,极端波浪波高越大。除此之外,随着谱宽的减小,极端波浪水平的不对称性也更加明显。极端波浪前端的波浪周期明显小于谱峰周期,尤其是最大波前第2个波浪;而极端波后的波浪周期基本等于谱峰周期。由于极端波浪前的周期小于波浪后的周期,根据线性色散关系,极端波浪前的群速也小于极端波浪后的群速,导致传递的能量在波峰附近聚集,这说明了线性色散关系对极端波浪的生成有着重要的作用,Lighthill[31]也给出了类似的解释,此时色散关系是极端波浪形成的重要原因。

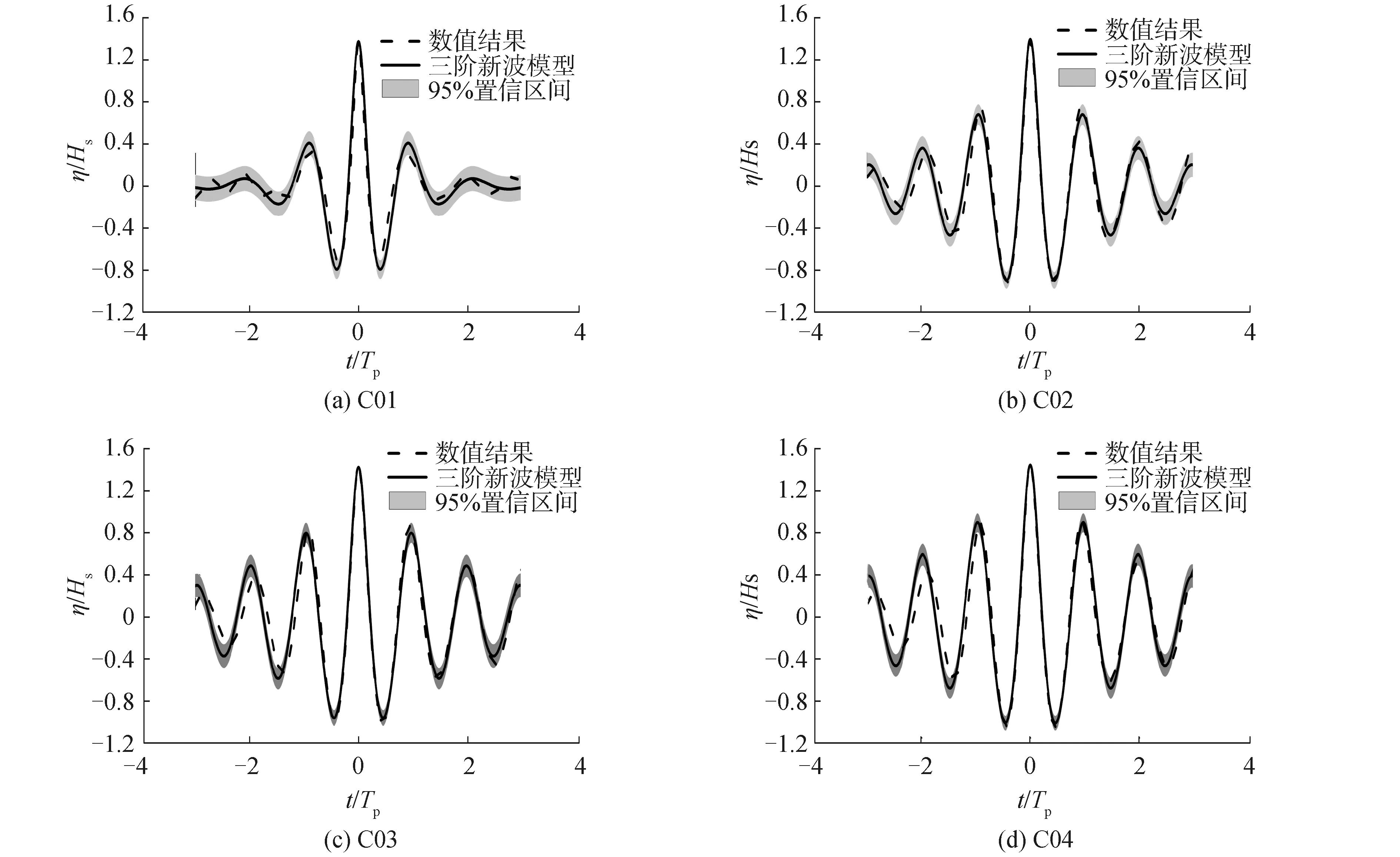
图1 C01、C02、C03和C04工况极端波浪平均波形与三阶新波模型对比

图2为谱宽相同,有效波高不同的4组工况模拟得到的极端波浪平均波形与三阶修正新波模型的对比图;从对比结果可以看到在波陡较大时,三阶修正的新波模型明显高估最大波峰两侧的波谷深度和波峰高度,超出三阶新波模型95%置信区间的范围;并且在有效波高较大的工况C06和C07中,数值模拟得到的极端波在波峰两侧更加陡峭;产生误差的原因有可能是因为当波陡更大时,波浪的非线性更强;另一个原因可能是因为三阶新波模型的推导是基于斯托克斯展开,只考虑了约束波的影响,并没有考虑自由波的共振对波高的影响。进一步观察模拟得到的极端波浪波形还可以发现:随着有效波高的增大,平均后的波峰高度与有效波高的比值分别为:ηc/Hs=1.40,1.44,1.46,1.45,波谷深度与有效波高比值分别为ηt/Hs=0.91,0.76,0.67,0.62;波峰波谷比值为ηc/ηt=1.54,1.89,2.18,2.34;结果表明当有效波高增大时,极端波浪的垂直不对称性显著增大。然而4组工况的极端波浪的无量纲波高分别为H/Hs=2.31,2.20,2.13,2.06,也就是说极端波浪的无量纲波高随着非线性的增加反而减小。在波陡较大的3组工况C05、C06和C07中基本没有出现水平周期上的不对称性,这可能是由于随着有效波高的增大,色散关系不再为极端波浪形成的主要原因,非线性已经成为主导,共振导致局部波谱变化。

所以总体看来,修正的三阶新波模型基本可以较好地描述极端波浪的平均形状;但是对于窄谱和波陡较小的工况,误差更小;在波陡较大时,实际波浪更为陡峭,新波模型会高估最大波峰两侧的波谷和波峰高度。极端波浪的波高随着谱宽的减小和波陡的增大而增大;而无量纲波高随着非线性的增加反而减小。在有效波高较小时,色散作用时极端波浪形成的重要原因;而当有效波高增大时,非线性占据主导作用,此时水平不对称性降低,垂直不对称性增强。

2.2 波高分布对比分析

Rayleigh分布是线性窄谱下的波浪理论分布,并没有考虑非线性的影响。MER分布考虑了峰度的影响,峰度值越大,说明该数据系列中的极端值越多。高斯分布的峰度值为3.0,若实际分布的峰度值大于3.0,则表示比高斯分布存在更多的极端值。由于波浪的非线性作用,实际海浪的峰度值大于3.0。

图3为有效波高相同,但谱宽不同的4组工况模拟得到的波高分布;从图中可以看到在H/Hs<2.0时,4种工况Rayleigh分布能够较好地预测波高分布,基本上和模拟的波高分布重合;当H/Hs>2.0时,Rayleigh分布明显低估了极端波浪的发生概率。2.02.5时,MER分布只在工况C02时与实验数据吻合较好,这是由于谱宽较窄时波浪的共振非线性作用增强(BFI增大),极端波浪出现概率增加,MER分布也不能准确描述极端波浪分布。

图3 C01、C02、C03和C04工况的累积波高概率分布与Rayleigh和MER分布的对比

图4为谱宽相同,有效波高不同的4组工况模拟得到的波高分布与理论波高分布的对比图。同样的Rayleigh分布低估了极端波浪发生概率,虽然MER分布比Rayleigh分布较好反映极端波,但仍会低估极端大浪的出现概率。

图4 C02、C05、C06和C07工况的累积波高概率分布与Rayleigh和MER分布的对比

图5给出了波峰分布的对比,可以看出Rayleigh分布、Forristall分布和二阶Tayfun分布都低估了大波峰出现的概率;Forristall分布和二阶Tayfun差别并不大,因为两者都是考虑了二阶非线性;而三阶Tayfun分布在ηc/Hs<1.25范围内与实验波峰分布吻合较好,而当波峰更大时,三阶Tayfun分布也会低估极端波浪发生概率。虽然三阶Tayfun也是在窄谱假定下得到的理论分布,但是从结果看来在宽谱下的结果也很好。

图5 C01、C02、C03和C04工况的波峰概率分布与理论分布的对比

图6也可以发现三阶Tayfun分布在ηc/Hs<1.25时基本与实验分布一致,误差主要发生在ηc/Hs>1.25时;波陡越大,高阶非线性作用增强,三阶Tayfun分布与实际结果相差越大;但是在有效波高最大的工况误差反而减小了。

图6 C02、C05、C06和C07工况波峰概率分布与理论分布的对比

3 结论

1)修正三阶新波模型能够较好地描绘极端波浪的波形;但是在波况的波陡较大时,实际波浪更为陡峭,并且具有明显的高波峰浅波谷的特点;修正的三阶新波模型会高估最大波峰两侧的波谷和波峰高度。极端波浪的波高会随着谱宽的减小和波陡的增大而增大,但是无量纲波高反而随着波陡的增加而减小。

2)当H/Hs>2.0时MER分布与实际波浪分布吻合较好;当波浪更大时,对于H/Hs>2.5时,MER分布只在部分工况与实验数据吻合较好,有效波高增大也导致MER误差增大。与MER分布类似,在波峰分布中,三阶Tayfun分布在ηc/Hs<1.25时基本与实验分布一致;谱宽越窄误差越大,有效波高增大误差也会先增大后回落。