增量动力分析与云图法在地下结构地震易损性分析的应用

蒋家卫, 王树旷, 许成顺, 杜修力, 陈国兴

(1.南京工业大学 岩土工程研究所, 江苏 南京 211816; 2.北京工业大学 城市与工程安全减灾教育部重点实验室, 北京 100124)

开发利用地下空间是实现城市可持续发展的重要途经之一。然而,在1995年日本阪神地震,1999年台湾集集地震和1999年土耳其Izmit地震中均观测到了地铁地下结构不同程度的破坏现象[1-3]。地下结构在地震中一旦发生破坏,具有经济损伤大,震后修复难等特点。传统安全或延性的抗震设计方法已不再满足当前结构抗震韧性的需求。基于性能的抗震设计理念旨在对结构震后的人员伤亡、经济损伤、修复时间等特征进行评估[4-5],是未来结构抗震设计发展的主要方向。地震易损性分析的工作可以评估结构震后失效概率,是基于性能抗震设计框架中的重要环节。

结构的地震易损性分析需要基于大量的震后破坏数据资料,数据的来源主要有以下3种途径:基于地震工程专家的意见、历史震害经验数据与数值分析方法[6-7]。随着计算机技术的迅速发展,目前基于数值模拟的地震易损性分析应用最为广泛[8],依据对地震动强度调幅手段的不同,又可分为云图法[9-10]、多条带法(multiple stripe analysis,MSA)[11]、增量动力分析方法(incremental dynamcal analysis,IDA[12-13]与耐震时程分析方法(endulance time method,ETM)[14-15]。云图法选用未经调幅的原始地震动记录进行结构的非线性动力时程分析,并基于最小二乘法对结构的响应与地震动强度参数进行拟合。MSA、IDA以及ETM方法则逐级输入幅值增大的地震动记录进行结构的非线性动力时程分析,以获取结构从弹性至弹塑性响应的全过程,通常采用极大似然估计法或线性回归拟合对结构响应与地震动强度参数关系进行预测。以上地震易损性分析方法在地上结构中的应用相对成熟,然而,由于地下结构抗震设计研究起步较晚,基于地下结构的地震易损性分析研究成果相对较少。仅有少数学者针对地下框架结构开展了地震易损性分析[16-23]。然而,目前尚未见不同数值地震易损性分析方法在地下结构应用的对比研究文献。

综上所述,本文以城市地铁车站地下框架结构横断面为研究对象,基于ABAQUS/Standard有限元软件平台,建立考虑土—结构相互作用的有限元模型。以峰值层间位移角为损伤指标,峰值加速度为地震动强度指标,分别基于云图法与IDA方法建立城市地下框架结构地震易损性曲线,并对2种方法所得到的结构震后失效概率进行对比研究。

1 地震易损性分析方法

1.1 地震易损性分析基本概念

作为基于性能抗震设计框架的重要组成部分,地震易损性分析旨在给出不同水平地震动强度作用下结构失效概率,主要包括2部分工作:结构概率损伤分析以及概率地震需求分析。其中,结构概率损伤分析的目的是为建立描述结构震后功能失效程度与结构响应之间的联系,即结构承载力限值,一般采用单一损伤指标进行描述。结构概率地震需求分析的主要任务是建立结构响应与地震强度之间的关系,在地震易损性分析中,其结构响应参数一般与损伤指标相对应。FEMA-P58[4]报告与FEMA-P695[24]报告均建议采用高斯分布函数模型来建立结构的地震易损性曲线,即:

(1)

式中:φ为标准正态分布函数;Sc为结构承载力均值;Sd为地震响应均值;βRTR由地震动记录所引起的不确定性;βC结构承载能力或建设质量的不确定性;βMDL分析模型的不确定性。

对于相同结构而言,其结构的损伤模型是一致的,因此,基于云图法与IDA方法的地震易损性的主要区别在于如何求解结构在地震动作用下的响应均值。

1.2 云图法

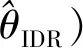
图1 地震动作用下结构的“云”响应(对数坐标)

(2)

云图法中结构响应的离散度可以通过计算数据的标准差获得:

(3)

1.3 IDA方法

IDA方法的核心是通过反复调整输入结构的地震动强度,以获得结构从弹性到塑性乃至破坏的全部反应过程。如图2所示,为基于IDA方法的概率地震需求分析步骤:

图2 IDA方法的实施流程

1)选取拟输入的地震动记录i(i=1),基于IPGA调幅至aj=1=0.05 g,进行土-地下结构体系非线性动力时程分析,获取峰值层间位移角。

2)若峰值层间位移角小于地下结构的倒塌极限,进入3)。若峰值层间位移角大于地下结构的倒塌极限,返回1),对下一条拟输入的地震动记录(i=i+1)重复1)的过程;当i=N(N为所选取地震动总条数)时,即计算完成。

3)令j=j+1,基于IPGA调幅至aj+1,例如,aj+1=0.1 g,再次进行土-地下结构体系非线性动力时程分析,并获取结构峰值层间位移角,返回2)。

4)确定峰值层间位移角的估计均值以及标准差。参考云图法,假设结构响应与地震动强度参数自然对数之间服从线性关系,采用线性回归拟合得到结构的响应均值与标准差。

2 算例概括

2.1 工程背景

为对比研究基于云图法与IDA法所建立的地下结构地震易损性曲线。本文选取北京4号线某浅埋地铁车站结构为研究对象,如图3所示,车站的横断面为2层双跨矩形框架形式,其断面整体尺寸为20.9 m×13.8 m(长×高),中柱截面为1 m×1.1 m, 侧墙厚度0.7 m,顶板厚度0.8 m,底板厚度0.7 m。结构中柱混凝土强度为C50,其他主体部分混凝土强度为C40,钢筋型号为HRB335。车站顶板埋深2 m,周边土层分布及其基本物理力学性质见表1,主要由砂土、黏土和粉土构成。

表1 岩土物理力学参数

图3 典型车站断面尺寸信息(单位:m)

2.2 有限元模型

如图4所示,为基于ABAQUS/Standard[25]软件平台建立考虑土-结构相互作用的二维有限元模型,模型长度取车站横断面宽度5倍或以上,模型深度取至基岩面,共45 m。选用实体单元模拟土体,基于改进的Davidenkov骨架曲线的non-Masing本构模型描述岩土的动力非线性和滞回特性[26-27]。选用梁单元模拟结构混凝土构件,采用塑形损伤本构描述结构在地震动荷载作用下的受拉-压力学行为[28-29]。选用桁架单元模拟钢筋,通过关键字*rebar定义在梁单元中,采用理想弹塑性本构模拟钢筋的力学行为[30]。为保证网格单元尺寸小于地震波长的1/10[31],全局尺寸取0.5 m,结构附近土体单元网格尺寸为0.25 m,结构与钢筋的单元网格尺寸均为0.25 m。为考虑土体与结构之间的动力相互作用,结构与土体接触面的径向采用硬接触,切向采用摩擦接触,其摩擦系数取0.4,这种假设已被广泛应用于地下结构地震数值分析方法的研究[32-34]。

由于需要考虑初始地应力,本文数值模拟过程分为2步:1)重力荷载,设置模型底部固定,两侧边界仅放开竖向的自由度,完成重力荷载的分析后,提取边界支反力;2)输入地震动荷载,在1)分析的基础上,将模型两侧边界设置为捆绑边界[35-37],即对同一高度的侧边节点进行运动耦合约束;导入1)重力计算结果的支反力与地应力,完成模型的地应力平衡。由于模型底部边界已经延伸至基岩面,本文采用振动法输入地震动荷载。分析过程中监测结构下层中柱节点N1与N2(图4)的位移时程曲线。

2.3 地震动记录

本文参考FEMA-P695报告[24],选取了22组远场地震动记录,共计44条加速度时程曲线,作为IDA方法的输入地震动荷载。基于PEER Ground Motion Database数据库[38]选取了251条远场地震动记录(包括IDA方法中的22条),共计502条加速度时程曲线作为云图法的输入地震动荷载,限于篇幅,这里仅列出上述地震动记录的加速度反应谱,见图5。

图5 地震动记录加速度反应谱(阻尼比:5%)

3 计算结果

3.1 回归分析

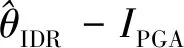
基于云图法分析所得到的回归模型:

ln(IDR)=1.11ln(PGA)+0.65

(4)

基于IDA分析所得到的回归模型:

ln(IDR)=1.06ln(PGA)+0.6

(5)

图6 基于不同方法计算所得数据样本的线性回归模型

3.2 地震易损性曲线

地震易损性曲线的建立不仅需要确定结构的概率地震需求模型,还需要建立结构的损伤模型,即定义抗震性能指标。Du等[39]结合地铁工程在城市生态环境中的重要地位,对地铁车站结构的震后性能水准进行了划分,并基于层间位移角建立了具有概率统计意义的地下框架结构抗震性能指标限值,因此,本文引用该文献所建立的层间位移角限值为损伤指标,见表2。此外,参考FEMA-P695报告[24],式(1)中结构与分析模型的不确定系数分别取βC=0.3,βMDL=0.2。

表2 矩形框架地铁地下结构性能水准定义

如图7所示,为结构基于云图法与IDA方法所得到的地震易损性曲线。受限于原始地震动记录信息的不足,基于云图法的地震易损性曲线仅给出了结构在地震动强度IPGA小于0.5 g以下的失效概率。相比于云图法,得益于调幅的优势,基于IDA方法计算的地震易损性曲线给出了任意地震动强度水平作用下结构的失效概率。由图7可知,2条曲线具有高度的重合性,由此说明基于云图法与IDA方法建立的地震易损性曲线非常接近。例如,当输入地震动强度IPGA=0.05g,基于云图法的计算所得到的地下框架结构性能水准1的失效概率为50%,而基于IDA方法计算得到的地下框架结构性能水准1的失效概率为52%;当所输入的地震动强度IPGA等于0.4 g时,结构基于云图法与IDA方法的计算得到的性能水准3的失效概率分别为67%与72%。以上结果表明基于云图法与IDA方法的地震易损性分析结果是一致的。为进一步阐述基于2种方法地震易损性分析评估结果的差异,定义参数Δp为2种方法计算结构失效概率的绝对差值,即:

图7 基于云图法与IDA方法的地震易损性曲线对比

Δp=|PIDA-Pcloud|

(6)

式中:ΔP失效概率的绝对差值;PIDA为基于IDA方法所得到的结构失效概率;Pcloud为基于云图法所得到的结构失效概率。

如图8所示,基于2种方法在不同性能水准的最大Δp分别为:性能水准1-正常使用为5.5%,性能水准2-可以使用为3.6%,性能水准3-修复后使用为7.5,性能水准4-不能使用为7%。可以看出,随着评估的性能水准等级逐渐递增,基于云图法与IDA方法的结构失效概率之间的差异会逐渐增大。但总体而言,基于云图法与IDA方法计算所得到的结构失效概率非常接近,其概率绝对误差最大值仅为7.5%。相比于地震动记录与结构模型中不确定性所带来的影响,上述差异在工程中基本可以忽略不计。

图8 失效概率差值计算结果

综上所述,基于云图法与IDA方法所得到地铁车站的层间位移角线性回归模型基本一致,虽然计算所得到的层间位移角标准差具有一定的差异性,但基于云图法与IDA方法计算的结构震后功能失效概率非常接近,最大绝对误差仅为7.5%。

4 结论

1)基于云图法:采用非线性动力时程分析方法获得了车站结构在502条远场原始地震动荷载作用下结构的峰值层间位移角;基于IDA方法:选取44条远场地震动加速度时程曲线,并基于PGA进行调幅,采用非线性动力时程分析方法获得了车站结构在调幅后地震动作用下的峰值层间位移角。采用最小二乘法原理,对分析所得到的层间位移角-PGA数据样本进行了回归分析,并在此基础上分别建立了基于云图法与IDA方法的结构地震易损性曲线。

2)基于云图法与IDA方法得到的线性回归分析模型非常接近,即采用2种方法所预测的结构峰值层间位移角响应均值基本相等,但基于2种方法计算的层间位移角的标准差具有一定的差异。进一步的地震易损性曲线对比结果表明:基于云图法与IDA方法所所预测的地铁车站结构地震易损性曲线吻合度较好,两者误差随着待评估性能水准的递增而增加,但所预测的失效概率最大差异仅为7.5%,与地震动记录本身或其他工程参数所引起的不确定性相比,该差异基本可以忽略。

3)由于受到地震波记录选取的限制,基于云图法的地下结构地震易损性分析仅能评估结构在相对较小地震动强度作用下的失效概率,得益于调幅的优势,IDA方法的评估范围则不受限制。