基于BP神经网络的传感器无效数据过滤器设计

王静文,王博文

(1.黄河水利职业技术学院信息工程学院,河南 开封 475000;2.中煤科工集团重庆研究院有限公司,重庆 400050)

0 引言

矿用传感器(如甲烷、氧气、硫化氢等传感器)构成了煤矿安全系统的感知层,对煤矿安全生产起着至关重要的作用。

市场上,矿用传感器大部分基于电化学原理。传感器敏感元件与被检测气体接触后发生电化学反应。电化学反应会引起传感器内部电桥输出电压发生变化。传感器处理器可以根据电桥输出电压的变化,计算出被检测气体的浓度。当传感器工作环境内的可燃气体浓度较大时,煤矿安全监控系统会立即执行断电操作,通过断开井下输电线路来避免瓦斯爆炸事故。在矿井环境下,电化学传感器受到诸如电磁干扰、湿度、震动、杂质气体等复杂因素的影响,会不可避免地产生无效数据。无效数据会引发电化学传感器的错误告警现象。错误告警往往被安全监控系统当作危险信号而执行断电操作,会造成不必要的损失。

国内外对传感器检测精度及误差的研究很多,但是没有反向传播(back propagution,BP)神经网络技术用于模拟电化学传感器特性及无效数据过滤的研究。国内外学者对传感器误差的自动校正研究主要是通过数学模型预估传感器实时输出值,并将其与传感器实际值进行对比、判断、分析,从而调整误差。这种方法无法对导致传感器输出无效数据的各种因素进行有效识别。

本文在BP神经网络的电力施工进度预警方法研究[1]及电化学原理传感器特性曲线分析的基础上,结合其他相关神经网络的文献论述,着重讨论了神经网络技术在分析处理电化学原理传感器无效数据过滤时的技术先进性和可行性。本文设计了基于BP神经网络的传感器无效数据过滤器,以解决因无效数据而引起的安全监控系统错误断电问题。

1 催化传感器无效数据过滤原理

1.1 催化传感器无效数据分析

催化原理的可燃气体传感器中,常见的有甲烷气体检测传感器。

甲烷传感器故障现象及原因如表1所示。

表1 甲烷传感器故障现象及原因

1.2 催化检测气体浓度原理

电化学可燃气体检测传感器利用催化无焰燃烧的热效应原理,由检测元件和补偿元件(俗称黑、白元件)构成测量电桥,以检测可燃气体浓度。

传感器处理器根据测量电桥中检测元件电阻阻值变化导致的输出电压信号,计算被检测的可燃气体浓度。其具体原理是,在一定温度条件下,可燃气体在检测元件载体表面及催化剂的作用下发生无焰燃烧,使检测元件温度升高。此时,检测元件内部铂丝电阻阻值也相应变大。这样电桥就会失去平衡,并输出1个与可燃气体浓度成正比的电压信号。通过换算,即可计算出可燃气体的浓度。

催化类传感器检测电路由检测元件、补偿元件以及滑动变阻器构成。电路的a点接在单片机模拟/数字(analog/digitalg,A/D)采样的PA1输入口,b点接地。补偿元件相比检测元件内部没有铂丝,主要用于温度补偿,以避免电桥零点漂移[2]。

催化传感器检测电路如图1所示。

图1 催化传感器检测电路图

Uo为a、b两端点电压。电桥的输出电压Uo1为:

(1)

式中:Vcc为供电电压;Rd为检测元件电阻;Rc为补偿元件电阻;R1、R2为变阻器上下2个部分电阻。

本文令R11=2+R1、R12=2+R2。电桥平衡时,R11=Rd、R12=Rc。当空气中有可燃气体(如CH4、H2S)时,黑元件Rd阻值增加ΔR(ΔR为电桥失去平衡后,检测元件Rd的电阻增加值),相应的Uo电压值升高。此时的输出为:

(2)

因为ΔR远小于R11+R12,所以:

(3)

Uo3与黑元件Rd电阻的变化呈线性关系。当可燃气体浓度增加,Rd呈现非线性变化时,Uo也呈现非线性变化。

1.3 传感器无效数据过滤依据

催化原理的传感器一般在检测到环境的可燃气体浓度变化时,会有一段响应时间。检测元件中的催化剂与可燃气体无焰燃烧,会引起铂丝电阻变化。检测电路有从微小的输出电压信号到输出电压信号稳定之间的时间间隔[3]。响应时间过后,传感器检测数据的输出会趋于稳定。基于以上原理,可以根据传感器响应时间内检测到可燃气体浓度数据的响应曲线是否异常来判断传感器数据的输出是否异常,从而采取进一步的过滤措施。

催化原理的传感器响应曲线是非线性的,所以可以采用神经网络技术解决响应曲线的识别归类问题。该技术将响应曲线分为正常、异常两种,通过滤除异常响应的数据输出而达到无效数据过滤的目的。

2 BP神经网络模型设计及性能测试

2.1 列文伯格-马夸尔特算法

列文伯格-马夸尔特(Levenberg-Marquardt,L-M)算法是使用广泛的非线性最小二乘算法。L-M算法是高斯-牛顿算法的改进形式,既有高斯-牛顿算法的局部特性,又有梯度法的全局特性。L-M算法的迭代方程为:

xk+1=xk-(H+αI)-1G

(4)

式中:H为多维向量的Hessian矩阵(因为H是矩阵,所以这里要用矩阵形式表示步长);G为多维向量的一阶梯度;I为单位矩阵;α为步长;xk为当前权值;xk+1为迭代产生的权值。

式(4)在高斯-牛顿式的H上加入α。当下降太快时使用较小的α,可以使式(4)接近高斯-牛顿算法;当下降太慢时使用较大的α,可以使式(4)接近梯度法[4]。

L-M 算法的平方误差式为:

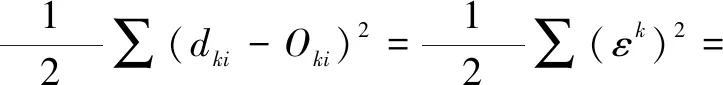
(5)

式中:dki为系统期望输出值;Oki为输出层第k个神经元的实际输出;ε为以εk为元素的向量;E为平方误差。

第k次向第(k+1)次迭代计算的E的误差函数式为:

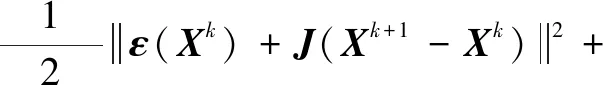
(6)

式中:J为雅克比矩阵;Xk、Xk+1分别为第k次和第(k+1)次的输入向量;μ为数学期望。

由于L-M算法兼顾了梯度下降法和高斯-牛顿算法的优点,所以在收敛速度和精度方面具有较高的效率。下面将利用L-M算法构建神经网络,并与梯度下降法和高斯-牛顿算法进行对比分析[5-6]。

2.2 BP神经网络模型设计

2.2.1 样本取样

已知甲烷传感器所检测到的甲烷气体浓度与检测电路输出电压Uab呈线性关系,则:

G=AUab+B

(7)

式中:G为甲烷气体浓度值;A为直线函数的斜率;B为直线的截距。

本文在实验室环境下对传感器进行零点和截距的校准,并作老化试验,使传感器处于测量稳定状态。本文取10只甲烷传感器,分别在甲烷浓度为6 000×10-6、8 000×10-6、10 000×10-6的情况下进行试验。

甲烷传感器响应特性曲线如图2所示。

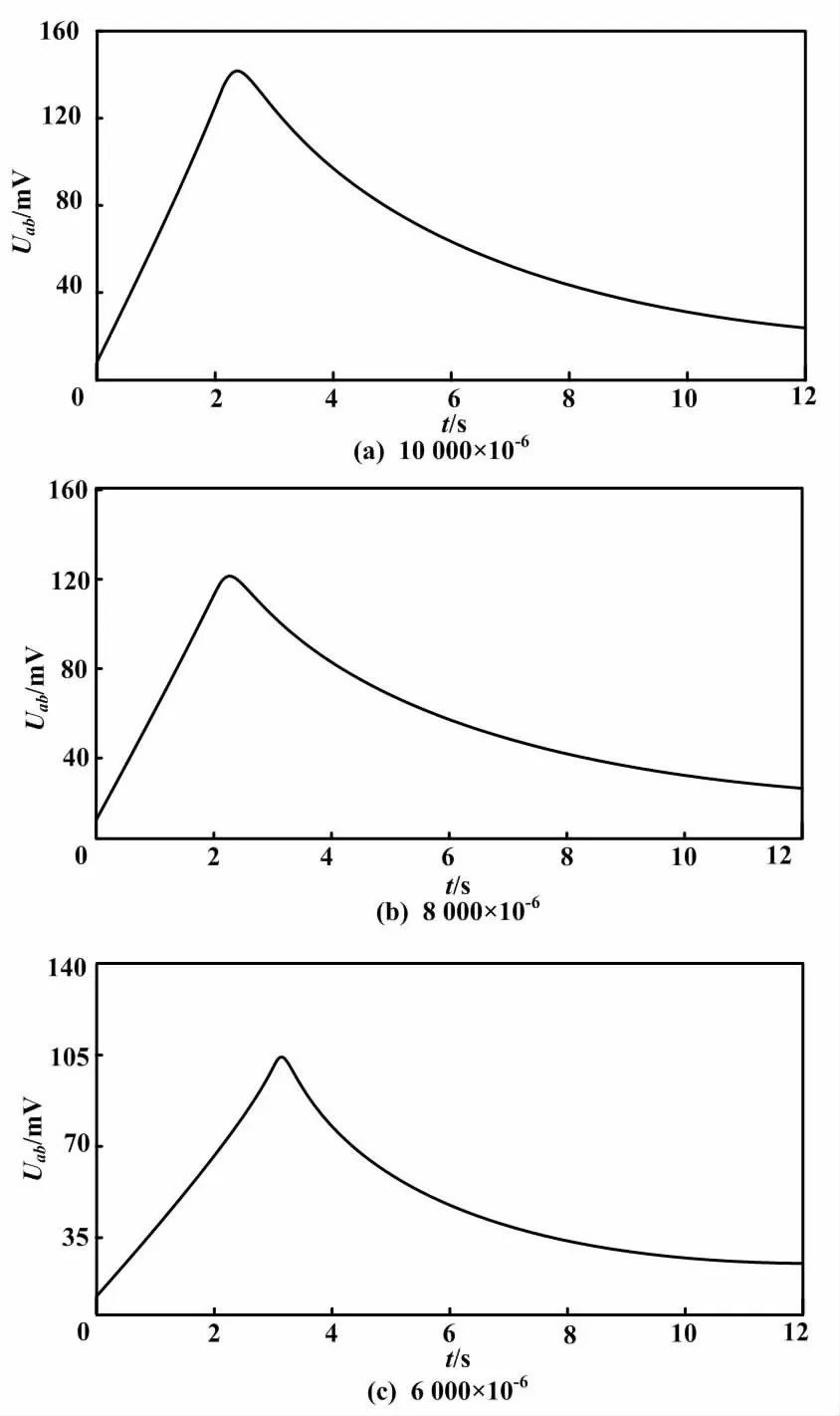
图2 甲烷传感器响应特性曲线

图2中,设t=0 s时为t0、t=2 s时为t1。

由图2可知,传感器对甲烷气体的响应曲线基本一致,从t0开始快速上升,到达t1左右经过了1个波峰,然后迅速下降至水平状态。

本文以图2曲线为样本素材,每隔1 s进行1次采样。每次试验以10个点作为1个样本数据。试验共有30组正常样本数据。试验使用传感器在异常状态下(包括断丝、电磁干扰、单片机故障、催化元件故障等情况)构建30组异常样本数据,即共有60组样本数据。

根据传感器数据类型的不同,本文将传感器数据分为有效数据和无效数据2种。有效数据经过神经网络后的预期输出结果为0.9。无效数据经过神经网络后的预期输出结果为0.1。

网络模型输入样本及期望输出如表2所示。

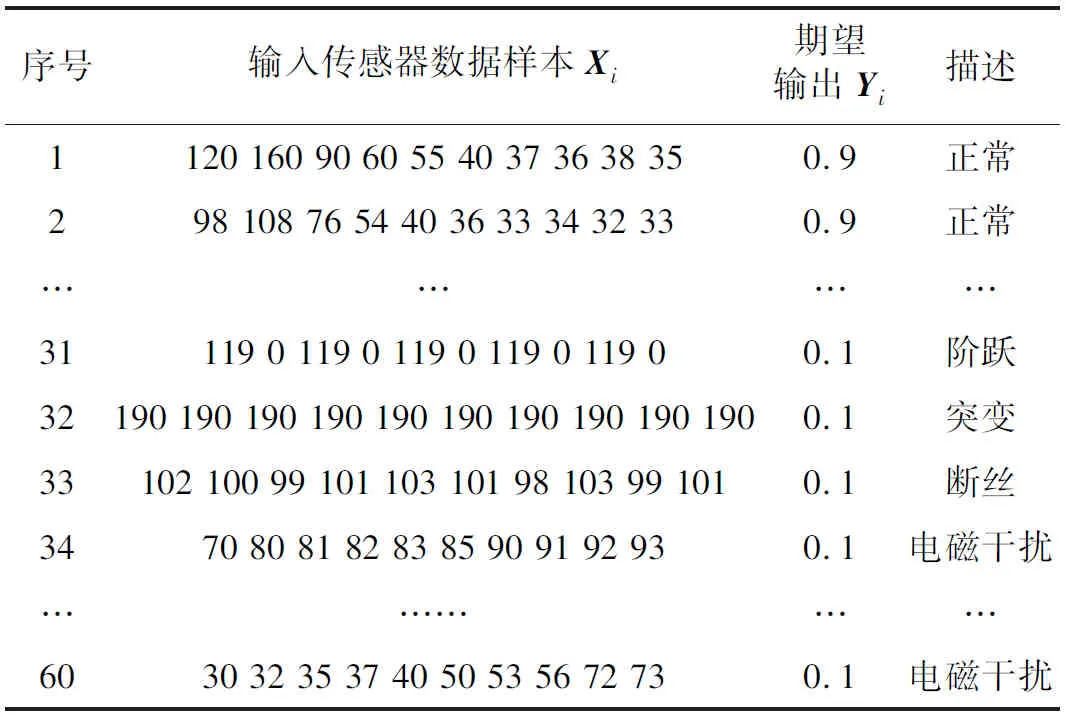
表2 网络模型输入样本及期望输出

2.2.2 模型构建

BP神经网络中间节点数量的计算式为:

(8)

式中:h为隐藏层神经元个数;m为输入层神经元个数;n为输出层神经元个数;β为1～10之间的调节常数。

由于输入的向量有10个属性值(即m=10)、输出只有1个概率值(即n=1)、a取2,所以h=5即中间节点取5个。

本文将甲烷传感器的响应时间参数作为输入样本的10个属性、输出的yi值作为该样本接近真实值的概率,以构建BP神经网络。

BP神经网络设计如图3所示。

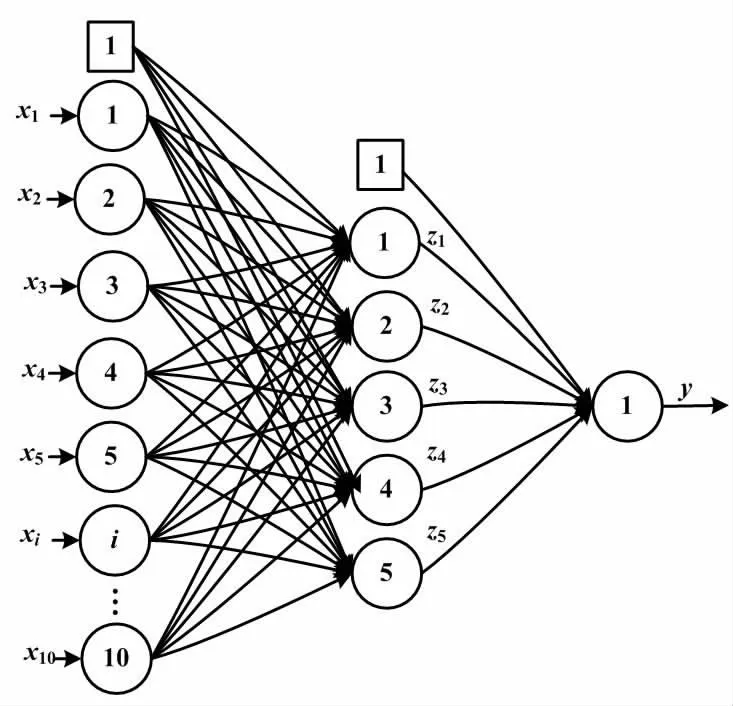
图3 BP神经网络设计图

X=[x1,x2,…,xi,…,x10]T。Wj=[wj1,wj2,…,wji,…,wjm]。若视x0= 1、wj1=bj,则X=[x0,x1,…,xi,…,x10]T、Wj=[wj0,wj1,…,wji…wjm]。隐藏层节点j的输入Zj为:

(9)

式中:f1为非线性激活函数;wji为权值;xi为输入向量X的第i个元素值。

输出节点y可以表示为:

(10)

式中:y为输出节点值;vj为隐含层至输出层的权值;f2为线性变换函数。

集合将上述60个样本作为输入,并以x1,x2,…,xp,…,x60表示。第p个样本输入神经网络后得到yp。第p个样本的误差Ep可采用平方误差的方式计算。

(11)

式中:A为单个样本节点输出误差值;tp为期待输入;yp为实际输出。

(12)

式中:B为有样本的全局误差;t为期望输出向量;y为实际输出向量。

t=[0.9,0.9,0.9,…,0.9,0.1,0.1,0.1]T。为使得全局误差B最小,本文调整wij和vj权值,使正常甲烷传感器响应曲线样本输出逼近0.9,而异常响应曲线样本输出逼近0.1。

2.3 网络模型性能分析

2.3.1 网络仿真及训练

根据以上输入、输出数据,隐含层以Tansig作为激活函数、输出层以Purelin作为激活函数,从而输出线性结果[7]。按照上述的神经网络模型选择不同的训练算法进行训练。样本训练过程如下。

①初始化神经网络的权值和阈值,设定修正步长,选取60组样本作为网络输入,并对样本作归一化处理。

②按照不同的训练算法,依次对网络模型进行训练。

③设定期望误差,当网络的训练次数达到设定的期望误差时,停止训练。

④判断训练次数是否大于迭代次数:若大于迭代次数,则结束;否则,按照步长修正权值转到步骤②。

⑤对不同算法的网络仿真结果进行对比,以观察收敛速度、误差大小。

本文以自适应线性回归(linear regression,LR)动量梯度下降法、拟牛顿算法(即高斯-牛顿算法的改进算法)、L-M算法为训练算法,对样本数据进行仿真和检验,以分析各种算法的性能表现。自适应LR动量梯度下降法的训练次数为40 901次,耗时230 s,误差接近1E-3。

根据仿真结果,自适应LR动量梯度下降法误差性能分析如图4所示。

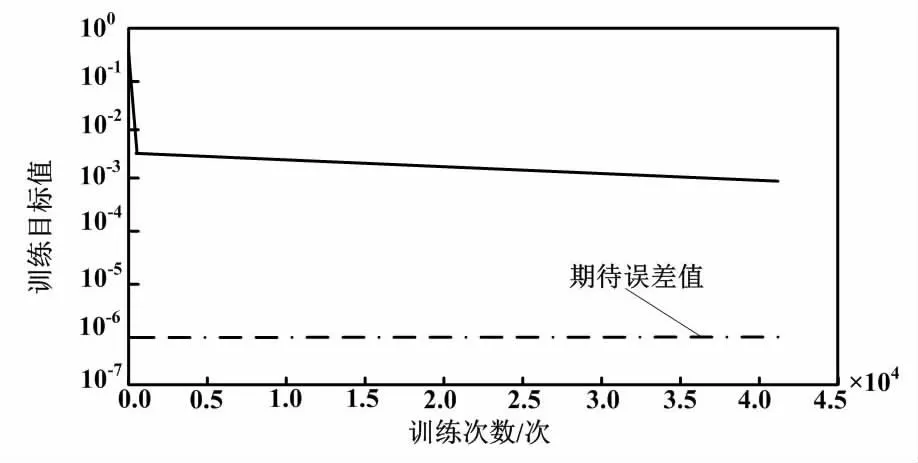
图4 自适应LR动量梯度下降法误差性能分析

拟牛顿算法训练次数为250次,耗时3 s,误差接近1E-4。

根据仿真结果,拟牛顿算法误差性能分析如图5所示。

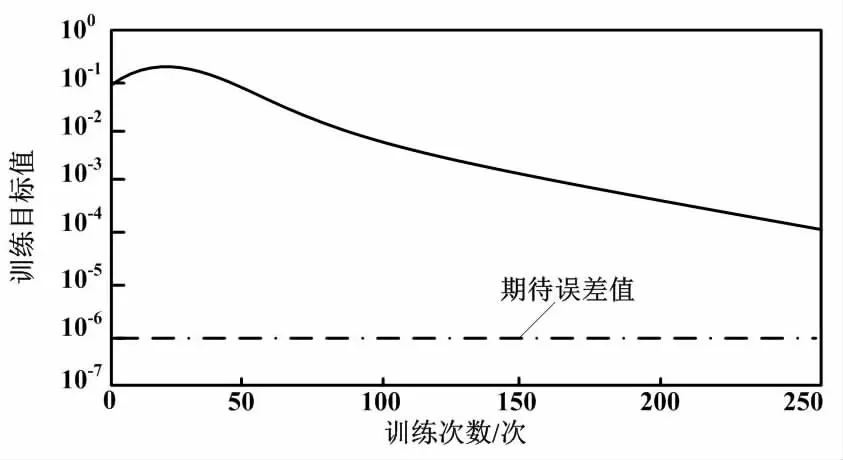
图5 拟牛顿算法误差性能分析

L-M算法训练次数为400次,耗时6 s,最小误差达到1E-6。

根据仿真结果,L-M算法误差性能分析如图6所示。

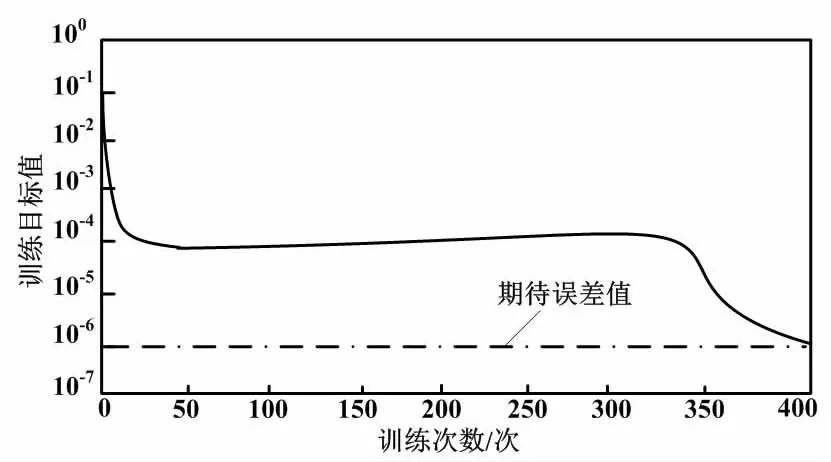
图6 L-M算法误差性能分析

相比较自适应LR动量梯度下降法, L-M算法具有较快的收敛速度和较低的输出误差。相较于拟牛顿算法,L-M算法误差小,且具有较高的收敛率[8]。所以本文选择L-M算法作为BP神经网络模型的建立基础。

2.3.2 L-M 算法误差性能分析

网络性能测试样本如表3所示。

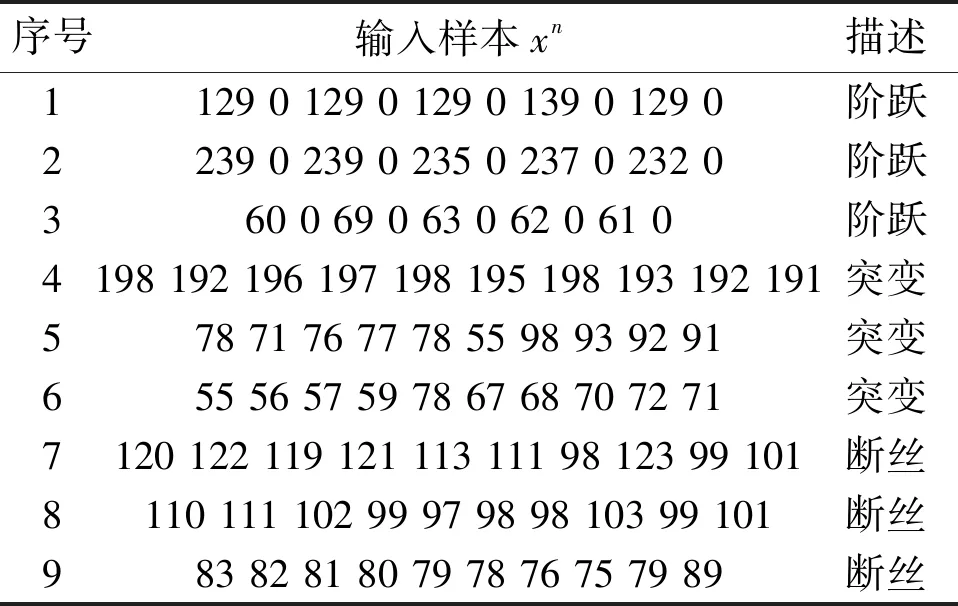
表3 网络性能测试样本

L-M算法训练误差达到最小值1E-6时,Matlab程序训练结束。传感器检测无效数据的9组测试样本输入BP神经网络模型进行训练。

L-M算法测试样本预测输出及输出误差如图7所示。

图7 L-M算法测试样本预测输出及输出误差

由图7可知,测试样本的L-M算法输出误差保持在0.02%以下。此算法过滤传感器无效数据的精度可以满足传感器系统非线性响应曲线识别的要求。当传感器的非线性特性曲线由神经网络识别后,正常响应曲线数据经过网络拟合的输出保持在0.9左右,而无效数据经过网络拟合的输出保持在0.1左右,并且具有较低的误差值。

2.4 传感器无效数据过滤器设计

为了过滤催化类传感器在实际工作中因为各种因素引起的数据无效问题,可以利用神经网络对传感器工作状态下输出的无效数据进行有效过滤。本文设计基于BP神经网络、L-M算法的网络模型。在实验室的环境下,将不同浓度的甲烷气体通入传感器,可得到传感器响应曲线离散数据。本文将数据分为正常数据和无效数据2大类,以得到X。本文构建传感器的输出向量Y,使输入向量X=[x1,x2,…,xn],与预期的输出向量Y=[y1,y2,…,yn]一一对应。在Matlab工具对网络模型训练时,可通过对比模型实际输出向量T=[t1,t2,…,tn]与预期输出向量Y来不断修改网络模型的权值和阈值,使输出均方误差趋于极小[9]。

算法在满足最小误差的情况下(0.02%以下)停止训练。停止训练后,网络模型以软件算法的形式内置于传感器,作为传感器实际检测数据输出的过滤器。该过滤器与实际的输出部分串联,通过调整设计门限值有效地过滤传感器的无效数据[10]。

3 结论

为了保障矿井可燃气体传感器的检测准确率以及矿井的安全生产、避免传感器无效状态对矿井安全生产造成的生产资源及时间浪费,本文基于BP神经网络模型的过滤器引入了传感器无效数据过滤检测机制。通过试验分析,本文得出网络模型对无效样本数据的识别误差低于0.02%的结论。通过网络模型有效过滤传感器的无效数据,可极大提高传感器的性能。同时,神经网络技术作为人工智能的基础,未来将更广泛地应用于传感器行业,以推动智能矿山的建设。