基于模糊场景聚类的微电网两阶段优化配置

米 阳, 李海鹏, 陈博洋, 彭建伟, 魏 炜, 姚 艳

(1. 上海电力大学 电气工程学院, 上海 200090; 2. 天津大学 电气自动化与信息工程学院,天津 300072; 3. 宁波电力设计院,浙江 宁波 315000)

化石能源的日益枯竭和环境污染的日益恶化,使得国内外学者不得不研究电力系统中的可再生能源发电技术[1].微电网作为接纳可再生电源的有效手段[2],逐步引起社会的广泛关注.但是随着全球厄尔尼诺现象加剧,天气情况越来越难预测.新能源发电装置的输出功率受天气影响巨大,因此,需对微电网各装置容量进行合理配置以平抑输出功率波动的影响,才能提高偏远地区供电网络在极端天气下的供电可靠性.

对于微网容量配置优化问题,国内外学者们已进行了大量研究.处理源荷两侧不确定性的不同方法对微电网的容量优化配置结果有重大影响[3].文献[4]中利用区间数学考虑风力发电(简称风电)的不确定性,继而构建含高比例风电的气电综合能源系统日前优化模型,但是没有考虑光照强度对系统的影响.文献[5]中采用机会约束的方法将不确定性变量处理为确定性变量,但是仅对光储一体化电站进行配置,没有考虑微电网的优化配置.文献[6-7]中用场景聚类优化的方法处理考虑多能源接入情况下的能源不确定性,但是对负荷侧的不确定性考虑较少.文献[8]中提出一种鲁棒优化的方法来快速处理风力和光照强度的不确定性,但是没有考虑极端天气对微电网优化配置的影响.鲁棒优化利用不确定集来描述概率分布,相比于其他规划,可以更加灵活地贴合实际情况[9-11].鲁棒优化可分为鲁棒线性优化和鲁棒二次优化.文献[12]中建立鲁棒线性优化模型,在考虑负荷和风电波动的条件下,一次性求出结果.文献[13-14]中采用鲁棒二次优化方法建立动态调度模型,根据第一阶段得到的决策变量对第二阶段的运行做出调整.目前,鲁棒优化在能源调度领域应用较为广泛[15-17],但在微电网容量优化配置领域应用较少[18].

场景聚类可以用来简化现有场景,将大量数据以一定的特征聚合在一起,得到典型场景,减少考虑场景的计算量.文献[19]中考虑大规模风电接入下对配网的影响,对风速进行场景聚类,但是未考虑风速和光照强度等天气因素对电网优化配置的影响.文献[20]中用场景聚类的方法考虑典型场景对系统灵活性的影响,但是未考虑一些极端场景对电网规划的影响.

基于以上分析,提出一种基于模糊场景聚类的微电网两阶段优化配置策略.在源端以风力和光照强度作为天气元素构建全年运行场景,从中利用模糊场景聚类的方法提取典型场景和极端场景.考虑极端场景下微电网的配置使其可以灵活应对不同天气情况下的运行状况.在负荷端以综合成本最小化为目标,并充分考虑负荷的不确定性,构建双层鲁棒优化模型.利用列和约束生成(C&CG)算法将模型分成目标不同却又相互影响的主问题和子问题,进一步利用Cplex求解器迭代求解鲁棒优化模型,最后基于算例分析验证所提策略的有效性.

1 微网设备数学模型

独立微电网模型如图1所示,由风力发电机、光伏电池、储能装置和微型燃气轮机组成.图中:AC、DC分别为交流、直流;Pload、PBESS、PDG分别为负荷功率、储能系统功率、分布式电源功率.

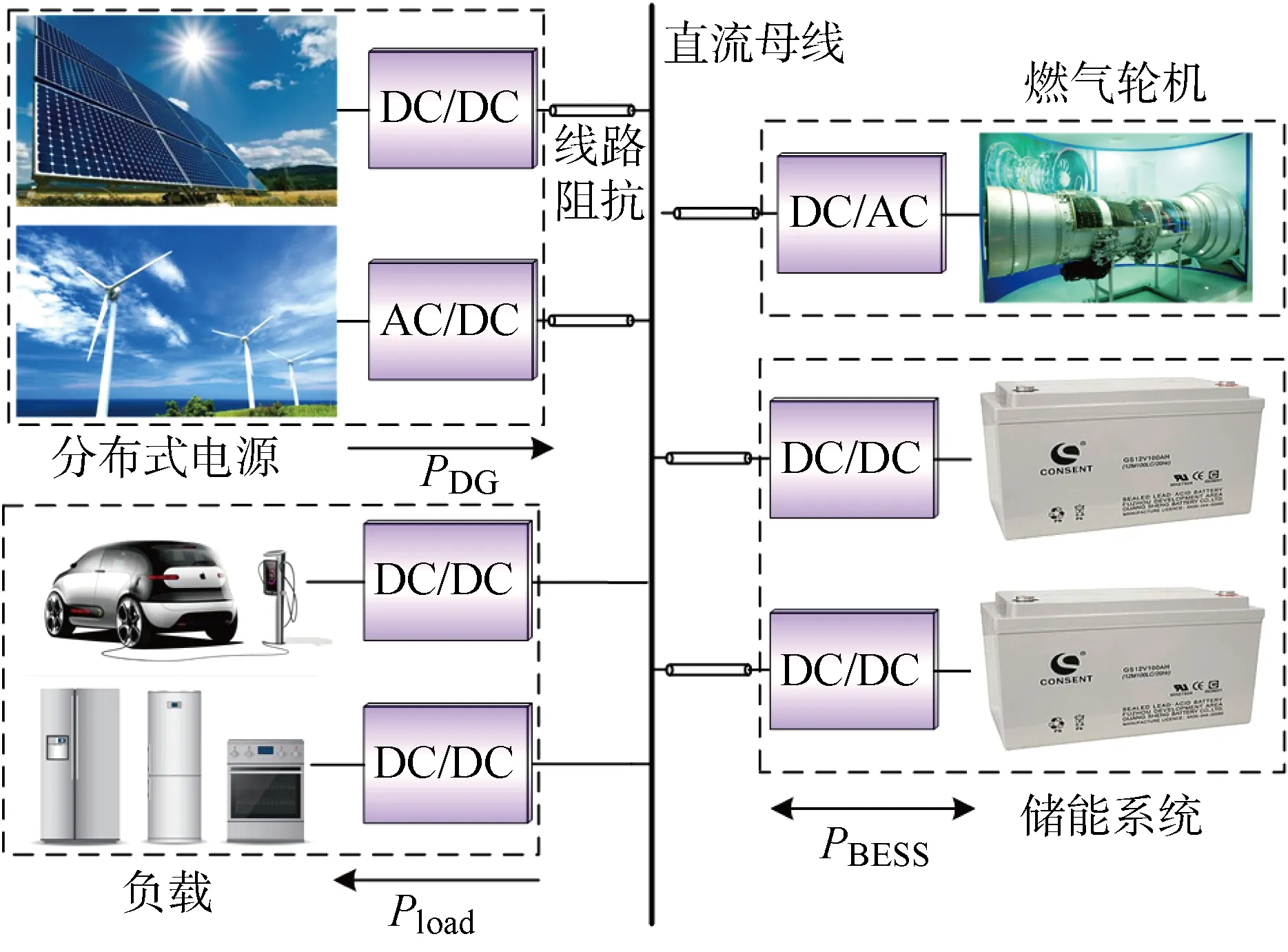
图1 微电网结构图Fig.1 Structure of microgrid

1.1 风力发电机数学模型

风力发电机出力主要与风速大小相关,风力发电机输出功率(Pwt)与当前风速(v)的关系函数可用下式描述:

(1)

式中:vF、vC、vR分别为风电机组切出风速、切入风速和额定风速;Pwt,N为风电机组额定功率.

1.2 光伏电池数学模型

为方便计算与建模,仅考虑光伏电池的输出功率与环境温度和光照辐射强度有关,其表达式为

Ppv=PSTCG[1+kpv(Tc-25)]/1 000

(2)

式中:Ppv为光伏出力;PSTC为标准试验条件下的最大测试功率;G为光照强度;kpv为功率温度系数;Tc为光伏电池工作温度.

1.3 储能装置数学模型

ses,t+1=(1-δes)ses,t+Pes,tΔtηes

(3)

-Pes,N≤Pes,t≤Pes,N

(4)

式中:ses,t为储能装置在t时刻的所余容量;δes为自放电效率;Pes,t为储能装置的充放电功率;ηes为充放电效率;Pes,N为额定充放电功率.

1.4 微型燃气轮机数学模型

Pmt,t=Ana,tηmtHmt

(5)

式中:Pmt,t为微型燃气轮机t时刻输出功率;Ana,t为天然气的总消耗量;ηmt为燃气轮机发电效能;Hmt为燃料热值,取9.7 (kW·h)/m3.

2 源荷侧不确定性处理方法

本文独立微电网需要考虑源、荷两侧的不确定性.源侧不确定主要指光伏电池和风力发电机出力的不确定性,而荷端不确定性即指负荷的波动性.针对极端天气对微电网中光伏和风电出力影响的不确定性,在随机优化过程中考虑极端场景对优化配置的影响.针对负荷出力在一个范围内波动的特性,考虑用鲁棒优化处理,并用基数不确定集表示.

2.1 随机优化处理风力和光伏不确定性

使用随机优化中的场景聚类技术解决风力和光伏不确定性.在规划的处理过程中考虑风光生成的多个天气场景,过多的场景会使得规划求解的流程复杂化,而过少的场景则会影响规划结果的准确性.因此,使用现有的风力及光照强度以小时为时间尺度的全年数据,建立规划水平年运行场景.利用模糊C均值聚类(FCM)方法,聚类得到典型场景.利用FCM考虑场景隶属度的特点,可以选取在整个运行周期场景中隶属度较大或者较小的场景,作为规划时所考虑的场景.这里假定数据集为X={x1,x2, …,xn},X的a个子集分别为X1、X2、…、Xa.

首先定义第j个样本xj对于子集Xi的隶属度为uij,与一般硬划分的隶属度不同,模糊C均值聚类利用模糊理论,隶属度在0～1内取值.目标函数J的实质是所有点到所有类的欧氏空间距离总和,表示为

(6)

(7)

式中:C为聚类中心数;N为样本数;m为聚类分析法的簇数;ci为第i个聚类中心.

用拉格朗日法把条件极值问题转化为无条件极值问题时,需要引入n个拉格朗日因子(λn),得到下式:

(8)

将式(8)分别对uij和ci求导得到:

(9)

(10)

可以看出式(9)和式(10)互相包含.先给ci赋予一个满足初始条件的值,将式(9)得到的结果带入式(10),从而得到uij,利用交叉迭代的方法迭代运算ci和uij的值.当目标函数J最终符合收敛条件时,聚类完成.

2.2 极端场景的选取

模糊C均值的聚类方法不仅可以实现硬划分场景聚类技术的功能,而且还可以得到每个场景相对聚类中心的隶属度.聚类中心和隶属度函数相互迭代得到最能代表规划年运行场景的聚类中心,作为规划所用的典型场景;在优化配置的过程中,选取对所有聚类中心隶属度都较低的场景作为极端场景.

极端场景的定义分成两类:一类是从聚类方式入手,选择对每个聚类中心都隶属程度较低的场景;另一类从电网出发,选取分布式电源在极端天气情况下出力较小的场景.

2.3 鲁棒优化处理负荷不确定性

鲁棒优化最大的优点是可以使用不确定集来描述不确定性信息.由于不确定集不需要精确的概率分布信息,所以在处理不确定性问题时,鲁棒优化有独特的优势.合适的“不确定集合”以及相对应的鲁棒优化模型是鲁棒优化过程中需要考虑的.根据不确定信息的特点选取“不确定集合”是鲁棒优化处理不确定性问题的关键,当前研究中常采用盒式、多面体、椭球、基数性等形式描述不确定集合.而本文采用基数性不确定集合来描述负荷的不确定性,符合在一定区域内微电网负荷每天大体趋势不变,但在一个趋势内波动的特性.这种集合的特点是能对不确定参量偏移量的相对值进行调节,因此能够更准确地调节负荷的波动状况.不确定度大的集合波动比较大,优化配置的结果更加激进;不确定度小的集合波动比较小,优化配置的结果更加保守.因此,合适的不确定度可以帮助获得对于整个微电网更好的配置结果.

3 双阶段鲁棒优化配置模型及求解方法

3.1 目标函数

以综合成本最小为规划模型设计的基本目标函数为

minCall=min(Cint+Cope)

(11)

式中:Call为综合建设成本费用;Cint为投资年平均等价成本费用;Cope为年运维成本费用.

其中,利用等年值法得到:

(12)

式中:ρ为折现率;rwt、rpv、rmt、rbat分别为风力发电机、光伏电池、微型燃气轮机和储能装置的折现年数;cwt,int、cpv,int、cmt,int、cbat,int分别为风力发电机、光伏电池、微型燃气轮机和储能装置的单位投资成本费用;Ebat,max为电池装机容量;Cbat,i、Cpv,i、Cwt,i、Cmt,i分别为风力发电机、光伏电池、微型燃气轮机和储能装置1 d的运行费用.

3.2 约束条件

3.2.1装机容量约束

(13)

式中:Smt、Swt、Spv、Ses分别为微型燃气轮机、风力发电机、光伏机组、蓄电池的装机容量.

3.2.2电源出力约束

(14)

式中:Ppv,N、Pmt,N分别为光伏电池、微型燃气轮机的额定输出功率;Pwt,t、Ppv,t分别为风力发电机、光伏电池在t时刻的输出功率.

3.2.3功率平衡约束

Pload,t+Pes,t≤Pmt,t+Pwt,t+Ppv,t+Pesc,t

(15)

式中:Pload,t为负荷在t时刻产生的功率;Pesc,t为储能充电功率.考虑孤岛运行时的功率平衡状况,消耗的功率应该小于产生的功率.

3.2.4储能充放电功率约束

(16)

Pbat,max=μEbat,max

(17)

(18)

式中:Pbat,max为储能充放电功率的最大值;μ为储能功率上限和容量的固定的比例系数;ηes为储能装置的充电效率;Ubat,t为t时刻储能系统充电和放电的信号,1代表储能设备充电,0代表储能设备放电.

3.3 等效模型和不确定集

为了解决微电网中负荷功率的不确定性问题,将鲁棒优化的思想引入微电网模型中,构建微电网的两阶段鲁棒优化容量配置模型.其中一阶段目标函数为微电网的年度平均投资成本费用,二阶段的目标函数为微电网的运行成本费用.将约束条件分阶段归类后,两阶段鲁棒等效优化模型如下式:

(19)

式中:h(x)≤0为第一阶段约束条件,表示为装机容量约束;g(y,x,u)≤0为第二阶段的不等式约束条件,包含电源出力约束和功率平衡约束;l(y,x,u)=0为第二阶段的等式约束条件,表示蓄电池充放电约束.

第一、二阶段决策变量及不确定变量的具体公式如下:

(20)

该模型为线性规划问题,通常利用确定性优化方法求解.主要考虑负荷不确定性在微电网实际运行中的影响,负荷功率的波动范围在构建的基数不确定集内:

(21)

式中:Pload,min和Pload,max分别为负荷波动的下限和上限;ΔPload,max为负荷功率最大的波动偏差;Kt为t时段的不确定度参数.

3.4 求解算法

采用C&CG对两阶段的鲁棒优化模型进行求解.根据算法的基本原则,首先将原问题分解为两个问题:对整个算法过程起主导作用的作为主问题,受主问题结果影响的作为子问题.确定整个算法结果的上限和下限,并采用交替求解的形式对主问题和子问题的结果继续进行迭代,在运算的过程中不断引入与子问题相关的变量和约束,直到算法的上限和下限收缩到一定范围内.其中主问题是微电网的优化配置问题,子问题是在主问题求解得到的微电网的配置情况下,找到负荷朝着对整个微电网运行情况最不利的情况下变化的最优运行方案.主问题可以用以下形式表示:

(22)

式中:xk为一阶变量,表示各装置配置的容量;yk为二阶变量,表示各装置运行出力;a、b为目标函数对应的系数向量;c、d、e、f为常数列向量;α为中间向量;A、B、C、D、E、F为相应约束状态下变量的系数矩阵.

经分解后的子问题为

(23)

Ω(x,u)表示为给定一组(x,u)时优化变量y的可行范围,具体表示方式如下:

(24)

式中:Da、Db、Dc、Dd为第二阶段约束的对偶变量.根据强对偶关系把内层的线性问题转化为最大化形式,和外层的最大化问题结合,最终得到合并后的子问题.

(25)

式(25)在取到最大值时,不确定变量u的取值即为该式中所定义的不明确的边界.通过上述的推导和转换,最终可用C&CG算法对两阶段鲁棒模型解耦成的主问题式和子问题式进行求解.整个算法过程如图2所示,ε为极小值.

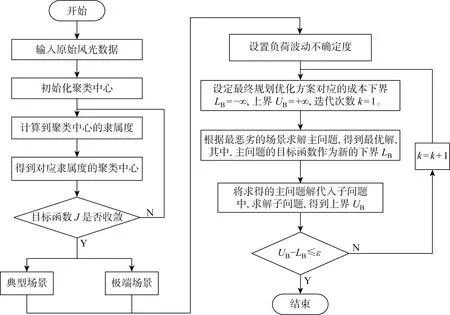
图2 算法流程图Fig.2 Flow chart of algorithm

4 算例分析

4.1 原始数据说明

以东部某偏远海岛模拟的天气场景为例,获得该区域全年的光照强度和风速数据,逐时数据如图3和图4所示,该地区年最大负荷为 1 884.79 kW,平均负荷为 861.42 kW.

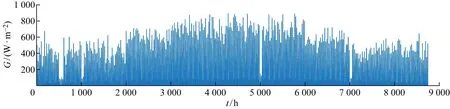
图3 全年光照强度逐时数据图Fig.3 Hourly data graph of annual light intensity

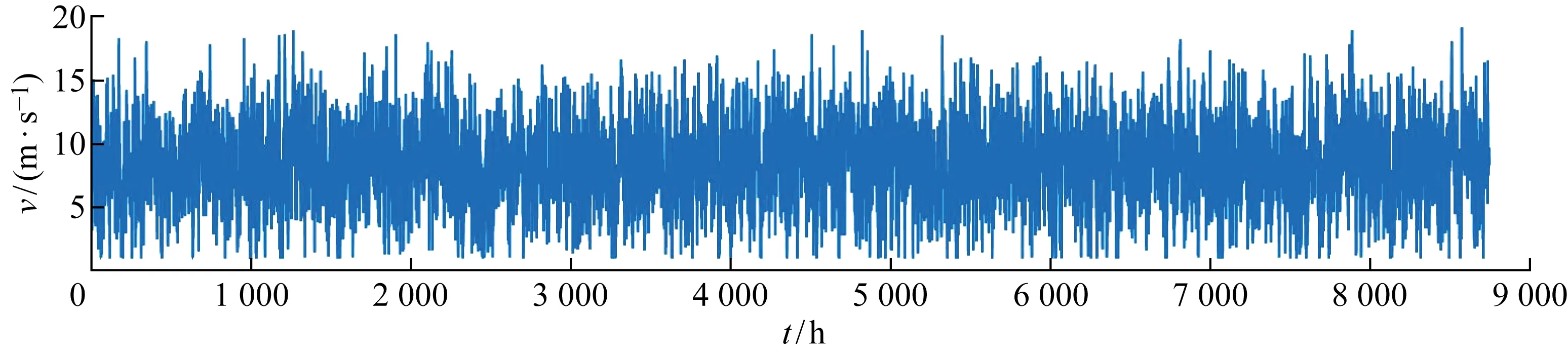
图4 全年风速逐时数据图Fig.4 Hourly data graph of annual wind speed

算例中的独立微电网包含微型燃气轮机、风力发电机、光伏电池以及负荷.设定微电网寿命年限为20 a,各种分布式供能与储能系统的规格选择部分参照表1所示的参数.蓄电池初始剩余电量设为0.8,荷电状态允许变化范围为0.1～0.9,充、放电效率分别为0.8和1.每小时最大充、放电量为其标称容量的20%,贴现率r取 0.05.

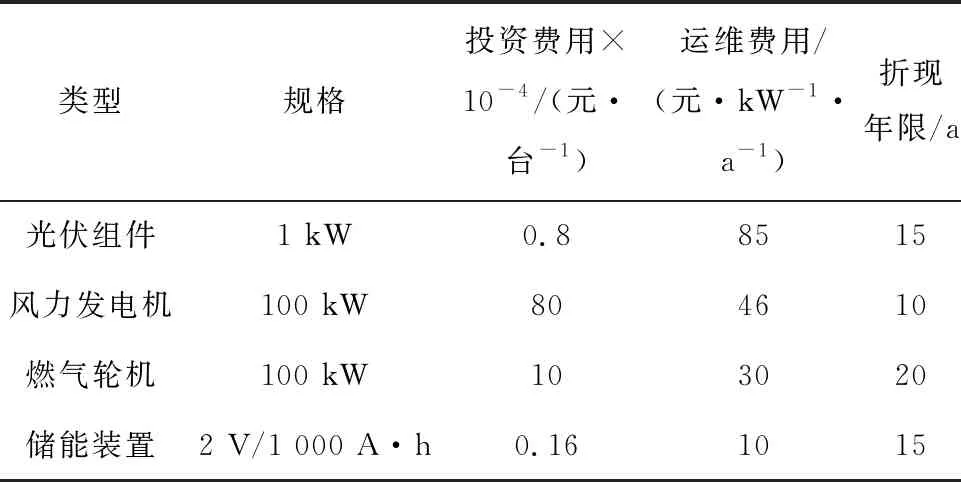
表1 优化配置算例相关参数Tab.1 Algorithm-related parameters

4.2 考虑不同场景对规划结果的影响

根据上述聚类方法,由实际光照强度和风力数据及负荷的年运行数据得出的场景集以及模拟运行用的聚类场景和极端场景如图5所示.图中:彩色圆圈表示由每个小时的天气状况构成的场景;黑色“×”表示聚类形成的典型场景;黑色“□”表示极端场景.因近年来极端天气的数量增加,用典型场景作为规划的依据已经不能满足微电网对供电可靠性的需求.为应对极端天气的影响,防止电力中断导致电力可靠性较高产业的损失,需要考虑典型场景和极端场景联合作为配置场景.由此得到光伏、风力发电机、柴油机和储能的配置结果,再与用典型数据得到的配置的典型容量进行对比.将负荷Pload波动的初始不确定度设定为0.15,如图6阴影部分所示.

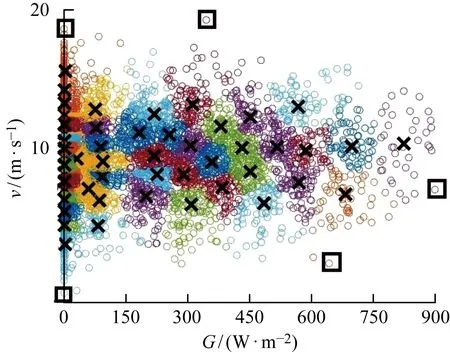
图5 光照强度和风速的场景集Fig.5 Scene set of light intensity and wind speed

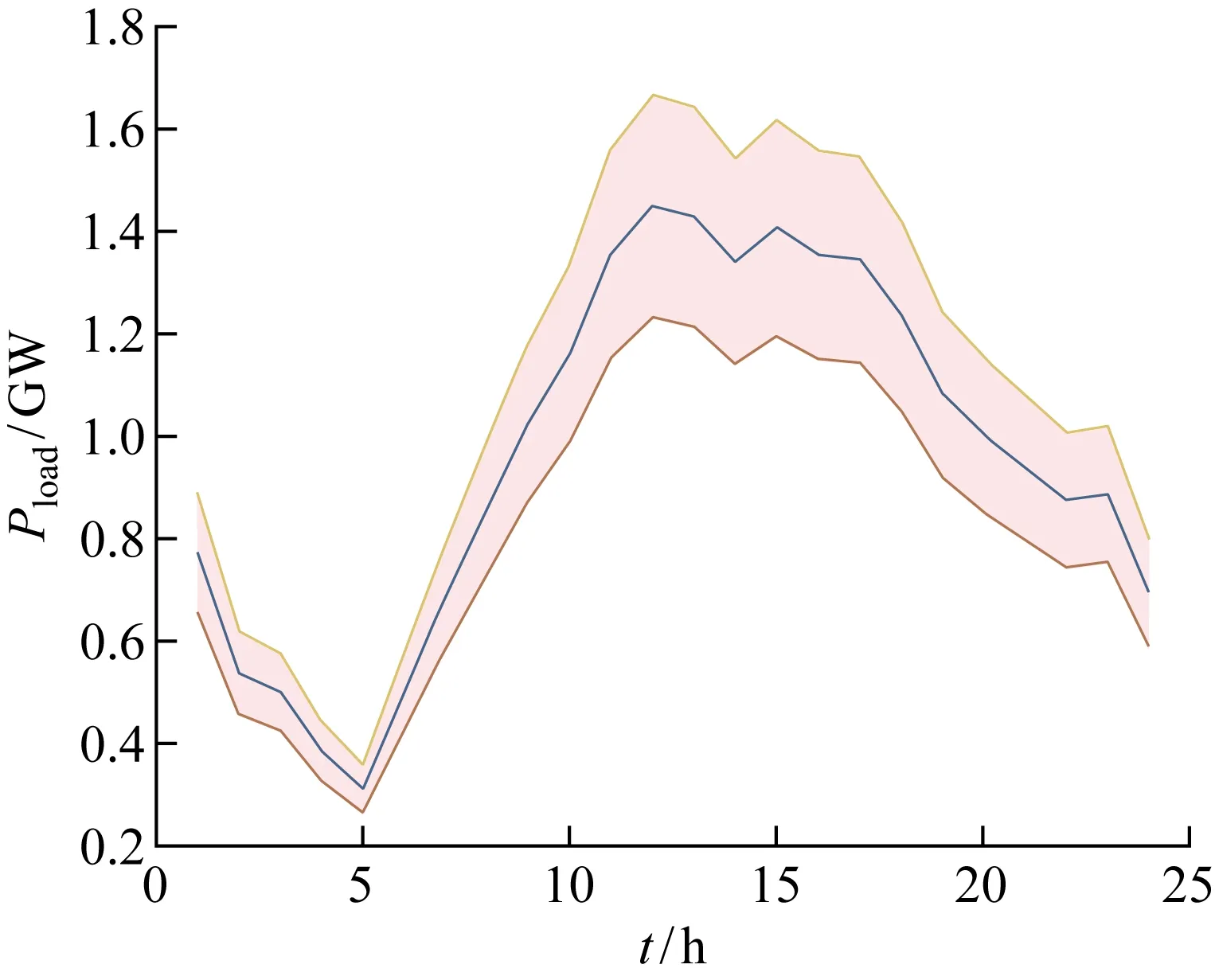
图6 负荷波动图Fig.6 Graph of load fluctuation

用典型场景进行仿真得到的结果命名为A;用典型场景和极端场景结合进行仿真得到的结果命名为B,具体配置如表2所示.由表2可以得出,与专门考虑典型场景得到的结果相比,考虑极端场景会对优化配置的结果产生显著影响,年投资成本增加55万元,失负荷概率降低0.705%.

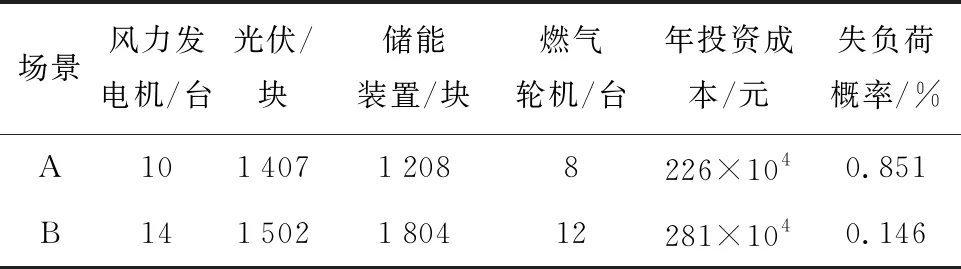
表2 考虑不同场景配置结果Tab.2 Configuration results of different scenarios

图7为典型日通过二阶段优化运行得到的功率(P)平衡运行结果.由图7可以看出,当负荷需求少于发电功率时,多余的电能给储能充电.在早午间时段(9:00—14:00)风力和光伏发电满足大部分负荷需求,多余的电能给储能充电;在夜间时段(23:00—07:00)依靠风电和柴油发电满足夜间大部分功率需求.

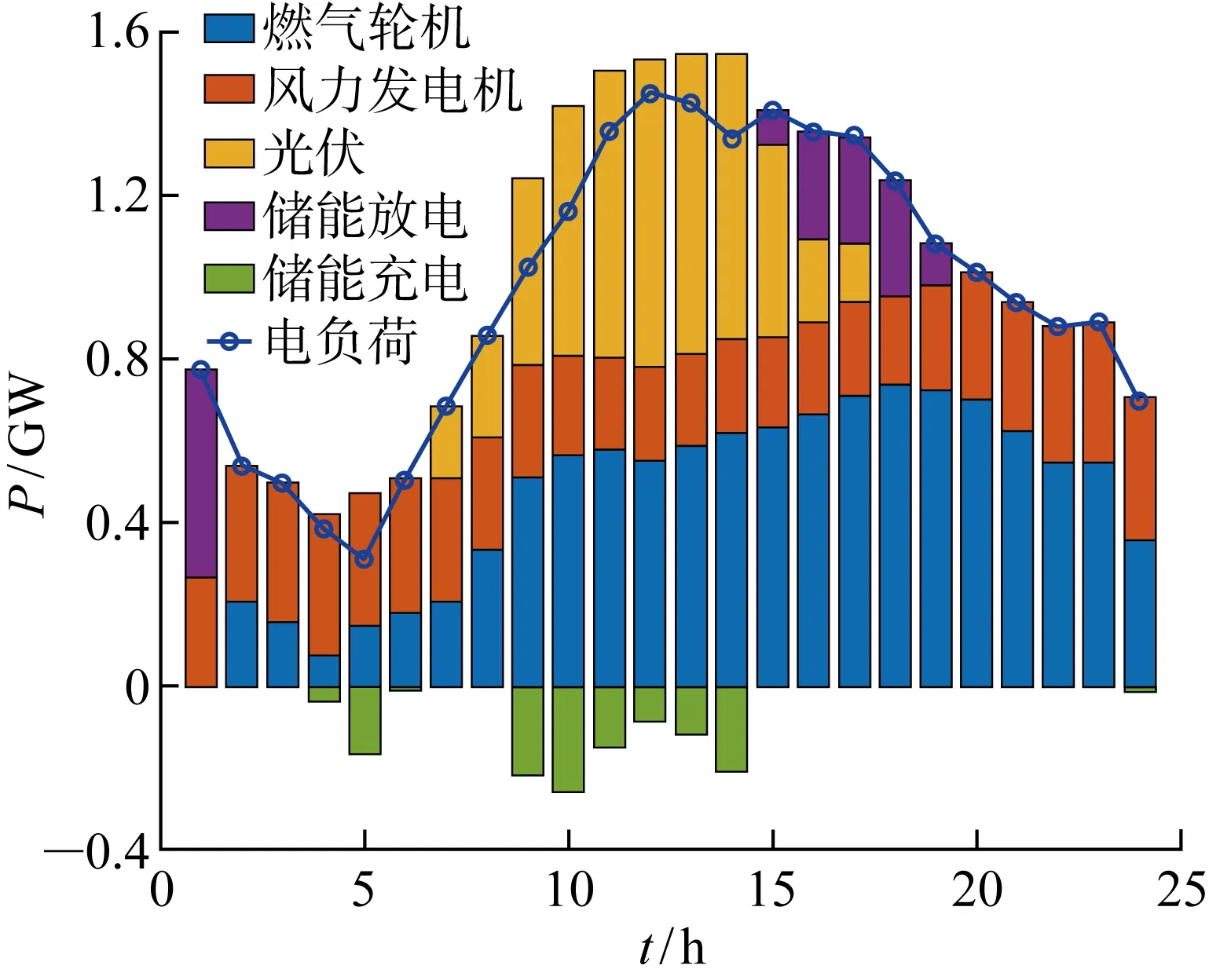
图7 典型日优化后的功率图Fig.7 Diagram of optimized power

4.3 负荷不确定参数对规划的影响

为比较不同负荷出力不确定度参数对系统调度成本的影响,分别设置不确定参数a′=0,0.15,0.25下的3种仿真场景,得到配置成本结果如表3所示.

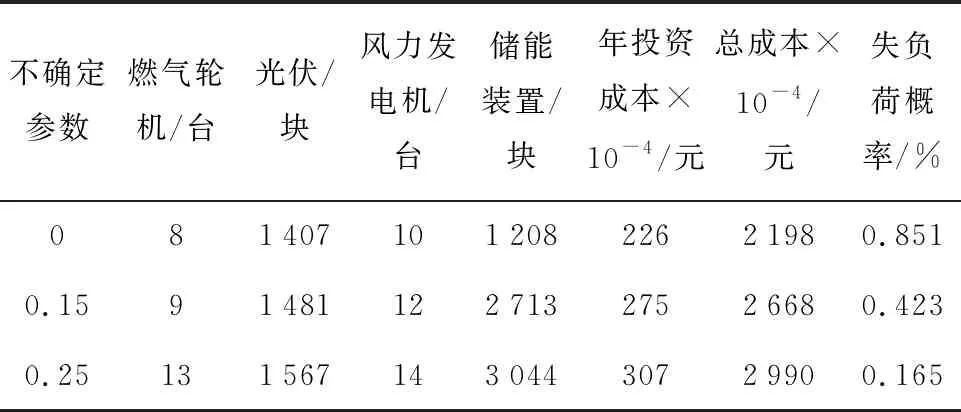
表3 不同负荷不确定参数下的配置成本

可以看出,在负荷确定的场景下,即不确定参数a′=0时,总成本是最低的.随着负荷不确定度的增加,微电网配置的总成本升高.而不确定参数为0、0.15、0.25时,对应运行成本分别为 201 755 元、250 345 元、273 475 元,可见运行成本随着不确定度增加而增加.

4.4 考虑不同方案对优化配置的影响

为比较本方案和其他方案的优缺点,考虑以下4种配置方案,结果如表4所示.

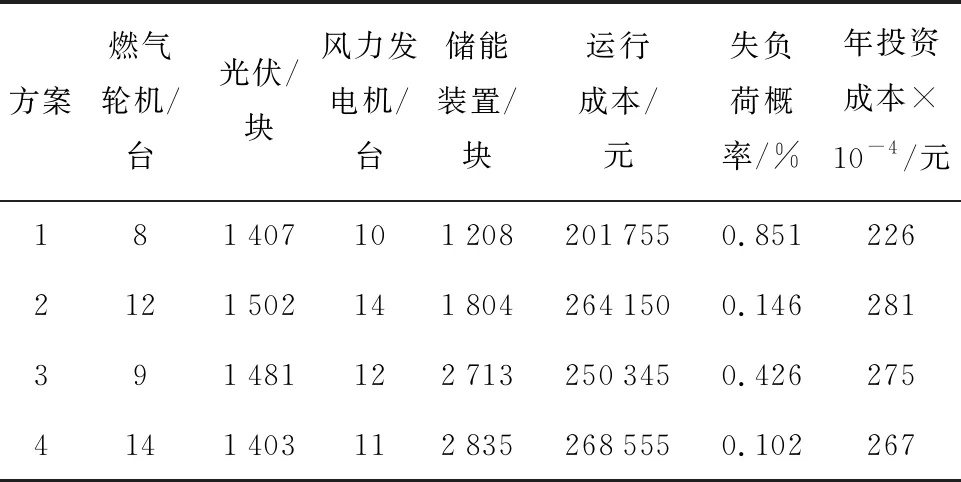
表4 考虑不同方案下的优化配置成本Tab.4 Optimal configuration cost of different schemes

方案1是考虑4个典型场景进行配置;方案2是在源侧考虑极端场景进行配置;方案3是在负荷侧考虑鲁棒优化配置;方案4是本文所提出的在源侧考虑风光不确定性、在负荷侧考虑负荷波动的方案.将失负荷概率作为衡量微电网可靠性的依据.与方案1相比,方案3考虑负荷波动运行在当前的运行场景的最恶劣情况,配置得到的微电网的可靠性得到提升,投资成本也升高;与方案1相比,方案2考虑极端场景对优化配置的影响,可靠性很大程度上增加.所提方法将方案2和方案3相结合,综合考虑年投资成本和运行成本,降低了经济成本且将电力不足概率控制在较低水平.

5 结论

考虑不同场景和负荷波动对微电网规划造成的影响,建立两阶段鲁棒规划模型;在一阶段配置微电网容量,在二阶段优化当日风光出力,用C&CG将模型分解为主问题和子问题,利用Cplex求解器迭代求解,分析结果表明:

(1) 所提模型考虑了负荷和可再生能源的不确定性.分别采用鲁棒优化和随机优化区别处理,微电网能够得到“最恶劣”场景下系统运行成本最小的规划方案.

(2) 通过改变不确定性参数调节,能够灵活根据当地环境考虑负荷的不确定度,按照合适的方案进行配置.

(3) 考虑极端场景对微电网进行配置,能够帮助微电网有效地应对极端天气对微电网的影响.

(4) 综合考虑不同方案对微电网优化配置的影响,该结论可以为微电网投资商在规划时提供参考.