高中数学导数课堂中渗透深度学习理念的探讨

周嘉炬

(利辛县第七中学 安徽亳州 236700)

上海师范大学数理信息学院教育技术系教授黎加厚曾指出,深度学习是基于理解性学习,通过发展自身的学科思维而获取新的知识。教师在指导高中生学习导数知识时,不能仅将目标设置在理解层面,还要发展学生理性的、有逻辑的数学思维,让他们在理解导数的同时不断获取新的知识,增强应用导数解决实际问题的能力和素养,促进他们对新知识的不断获得。

一、理念探讨——内涵与意义

将深度学习理念渗透在高中数学导数课堂中,首先要明确两个问题:第一,深度学习是什么;第二,深度学习有哪些作用,在导数学习中有哪些作用。只有准确把握了这两点,师生才能在课堂教学中做到有的放矢。

(一)深度学习的内涵

深度学习是一种相对浅层学习而言的学习理念。二者的区别主要体现在学习目的、学习过程、思维模式、记忆特点、学习能力几个方面,具体如下表所示(见表1)。

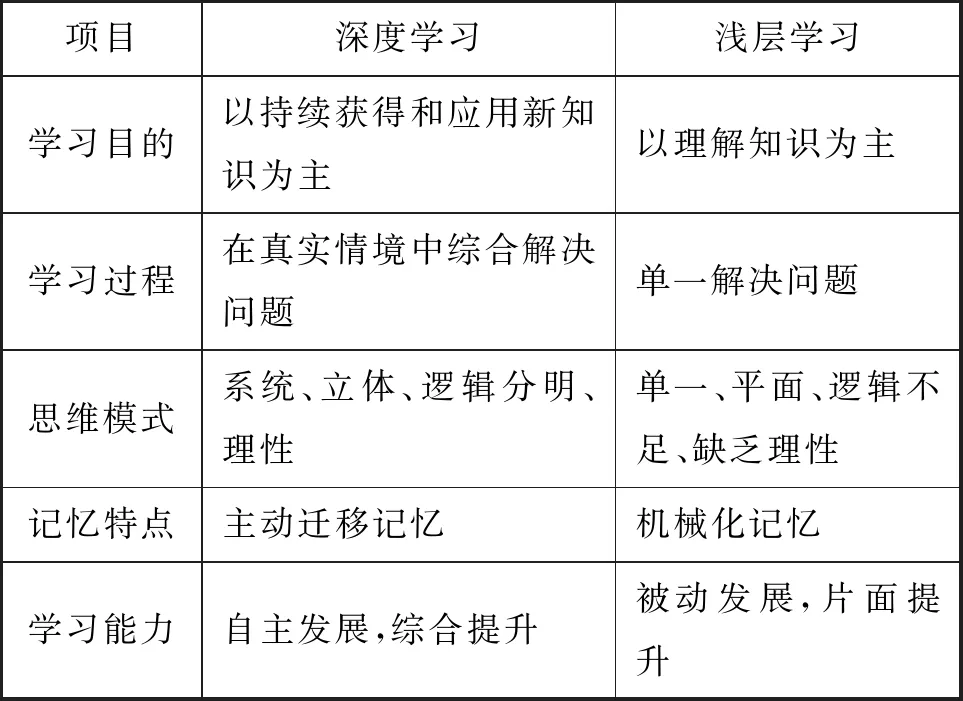
表1 高中数学深度学习与浅层学习内涵对照

(二)深度学习的意义

在浅层学习基础上,深度学习拔高了一个台阶,更加关注学习者知识、思维与能力的主动和持续发展,这对学生在高中阶段的数学学习意义重大。首先,学习目的与过程的变化,能够有效增加学生的主观能动性,促进其学习能力的自主提升。其次,随着学生学习能力的提升,数学课堂教学效率得到极大提高,师生充分利用课堂主阵地,全面地探索知识,合理分配理论探究与实践应用的时间,保障课堂教学质量。最后,随着思维模式、学习过程和知识记忆特点的变化,学生数学思维能够得到锻炼,能够因实践而经历高阶思维的建立和发展过程,大大增强思维品质,有助于发展学科核心素养。

二、实践探讨——导数课堂上的深度学习

(一)领悟

到底是知难行易还是知易行难,教育工作者们争论不休。笔者认为,高中阶段的数学课程,知与行难度不分上下,师生要给予“知”“行”同等关注。而在具体的学习中,唯有先“知”,才能达到“行”的目的。教师应先在“知”中渗透深度学习理念,让学生最大限度地领悟数学概念,吸收数学理论和思想。

1.说理:讲好概念第一课

说理,指的是讲明道理。新人教版高中数学教材导数第一课,安排的是“导数的概念及其意义”。这说明学生打破认知阻碍,明确“导数是什么”“导数有什么用”,是实现深度学习的第一步。而说理,是讲好概念第一课的有效方法。教师应将“概念及其意义”说清楚,同时引导学生将其中的道理说出来,使其在“眼到见理、耳到听理、口到说理”中,逐步达到“知理”的境界,实现向深度学习的有效靠拢。

那么,如何说呢?教师方面,情境的作用不容小觑。以“变化率问题”为例,教材以“高台跳水运动员跳水时的瞬时速度”和“抛物线切线的斜率”引出导数。教师可以基于“跳水”与“抛物线”创设情境。比如,利用定格动画还原高台跳水运动员在跳水时的瞬时画面,向学生说清楚“为了精确刻画运动员的运动状态,需要引入瞬时速度的概念,而运动变化的观点,是研究微积分的重要思想”这句话,同时结合教材案例,说明分析案例的基本过程。

而学生方面,对翻转课堂有比较特别的要求。教师应站在与学生平等的位置上,交还课堂主动权,使其成为课堂真正意义上的主人,培养其“敢说”的勇气,给予其“能说”的机会。比如,在通过白板出示抛物线f(x)=x2,创设问题情境“如何定义抛物线f(x)=x2在点P0(1,1)处的切线”的基础上,引导学生结合上述经验分析情境,说出“为了研究抛物线的切线,通常可以在已知点附近任取一点P1,考察抛物线割线P0P1的变化过程”等类似道理。

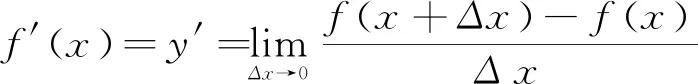
2.体验:注重运算和规则

深度学习导数概念后,高中数学导数课堂教学重点向运算方面倾斜,教师应引导学生在基本初等函数的导数学习中,研究导数的运算法则,使其能利用导数的运算法则和基本初等函数的导数求出复杂函数的导数。对此,体验是一个很好的学习方法。

首先,教师可以采取数形结合方法加深学生学习体验。以“基本初等函数的导数”一课为例,对于y=f(x)=c、y=f(x)=x、y=f(x)=x2几个初等函数,学生已经将其图象铭记于心。教师可以先基于y=f(x)=c进行示范,在几何画板中画出其函数图象,根据导数的定义,引导学生判断导数的存在条件,再指导学生画出其他初等函数图象,使其基于图象,体验基本初等函数的导数特点,发现“若f(x)=c(c为常数),则f′(x)=0”等规律。这种以数形结合为载体的自主学习,不仅优化了学生对“基本初等函数的导数”的学习体验,还能在图象与数的迁移对比中,加深其对基本初等函数导数公式的理解与印象,深度学习效果不言而喻。

其次,教师可以通过例题分析方式加深学生学习体验,在“导数的四则运算”一课中,进一步渗透深度学习理念。比如,通过课件出示例题:设f(x)=x2,g(x)=x,计算[f(x)+g(x)]′与[f(x)-g(x)]′。它们与f′(x)、g′(x)又有怎样的关系?随后,以[f(x)+g(x)]′为例,出示运算过程,让学生在例题分析与观察中,初步体验基本初等函数导数的四则运算规律,尝试说出[f(x)-g(x)]′的运算步骤。在此期间,教师应注意一个问题:由于学生刚刚体验基本初等函数导数的四则运算,思维逻辑尚不严谨,对其“说”的评价,不能局限在“对”和“错”上,而是要以“哪里说得有道理”“哪里说得还不够”为主。这样,学生更乐于在例题中体验,思考层层深入,才能真正把握[f(x)±g(x)]′=f′(x)±g′(x)等运算规律。

最后,在“简单复合函数的导数”一课中,教师可以通过项目任务加深学生学习体验,在此基础上,达到渗透深度学习理念的目的。这是因为,与“基本初等函数的导数”相比,“简单复合函数的导数”规律更难发现,很难通过图象观察直接得出,但若应用四则运算规律进行计算,多数情况下都能得出正确的导数答案。而“导数的四则运算”一课教学结束后,鲜有学生具备良好的简单复合函数计算能力,这就需要他们在项目合作中相互帮助、弥补不足。教师同样可以立足于教材例题,设定体验式项目任务,如四人一组,讨论如何求出函数y=ln(2x-1)的导数。由于高中阶段的学生已经具备较为成熟的学习态度和习惯,教师可以使其自由分组,实施项目任务。待其结束体验式学习后,要求各小组分别派出一名代表汇报运算过程和体验结论。这时,学生认真倾听,思考组间不同意见,围绕矛盾性结论展开辩论。这对深度学习是极为有益的。

3.探究:导数函数有联系

概念说理、四则运算,共同反映了一个事实——导数与函数存在千丝万缕的联系。函数的思想可以用来解决导数的问题,那么,导数的思想对解决函数问题有帮助吗?要想实现深度学习,必须明确其答案。这要求教师深入探究导数与函数的内在联系,找准函数与导数关联点(函数的单调性与导数的正负性;函数的极值、最大值、最小值与导数的0值),设计开放性探究活动。

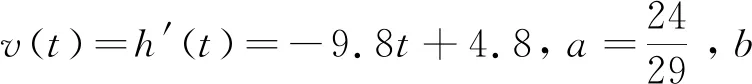
图1

图2

数形结合思想再次被渗透在课堂教学中,学生先对函数与导数表达式关联点展开探究,再在图象的对比中,讨论函数单调性与导数正负性的联系,直观地发现导数为正时,函数处于单调递增状态,导数为负时,函数处于单调递减状态,实现深度学习。

(二)实践

理论教学结束后,接下来就是实践。对此,教师一方面要用好教材,另一方面要注重高中数学导数课堂与高考导数真题的衔接,拓宽视野,为学生创造综合性解决问题的机会,有策略地为其制造挑战。

1.更上一层楼——用好教材

教材层面,应充分发挥课后练习题的优势。以“函数的单调性”一课为例,教材有这样一道习题:证明函数f(x)=2x3-6x2+7在区间(0,2)上单调递减。教师不仅要灵活利用课堂剩余时间引导学生完成该习题的解答,还要及时做好面批讲解,了解学生自主解题的答案,呈现正确的解题步骤,对错处进行讲解,校正学生错误思维。例如,在学生举手说明答案后,通过板书呈现解题步骤,同时根据不同步骤的重要性,追问:“这一步的用处是什么?”“下一步应该怎样展开?”“有的同学在这步出错了,对比一下,问题出现在哪里?”帮助学生完成对习题的深入思考,最终使其在有效实践中,实现“更上一层楼”的深度学习。

2.会当凌绝顶——对接高考

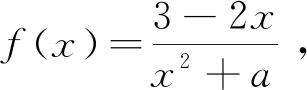
总而言之,用好说理、体验与探究的教学方法,加深学生对导数理论的领悟,同时立足课堂强化实践,在教材习题与高考真题的协同支持下,鼓励学生应用导数思想和知识,综合性地解决实际问题,是在高中数学导数课堂渗透深度学习理念的有效方式。教师要巧用以上方法,将深度学习理念循序渐进地渗透在高中数学导数课堂中,促进学生对导数的主动、理性、系统和深度学习,从而更好地提升其综合实践能力。